基于距离变换的A*搜索骨架提取方法*

唐姝 刘俊

（武汉科技大学计算机科学与技术学院 武汉 430065）

1 引言

一个对象的骨架被看作是其中轴，这个概念最早是由Blum提出的［1］。关于骨架的经典定义有两种：一种是火烧模型，其定义为火种从物体边界同时向物体内部燃烧，火种的相遇点就是中轴点即骨架点；另一种是最大圆盘模型，其定义为骨架即为包含在物体内部的，与物体边界至少有两个相切点的，所有不重合的圆的圆心集合。骨架可以有效地表示物体的拓扑结构和物体的形状特征。利用骨架对目标进行表示、识别，这些技术已经被广泛应用于路径规划、交通警察的手势识别［2］、考古学［3］、文学［4］、物料的分选［5］和信息存储检索［6］等领域。

关于骨架的提取方法，一般面临以下问题：1）提取骨架是否具有连通性；2）提取的骨架是否具有单像素性；3）提取的骨架是否逼近物体的中轴；4）在小的形变下，提取的骨架是否可以保持位置的稳定；5）提取的骨架是否保持原始物体的拓扑结构。

目前关于骨架提取的算法大致可以分为以下几类：骨架细化方法［7］，其核心思想是在物体边界上留下满足骨架提取算法要求的点，并去除其他冗余点。利用迭代的思想，将边界上的冗余点连续剥离，直到没有多余的边界信息为止，剩下的是提取的骨架。这种方法提取的骨架具有单像素性和连通性，但提取的骨架的位置，即骨架是否逼近物体的中轴不能得到保证，并且这种方法对边界噪声敏感，提取的骨架易产生冗余分支；利用物体距离场进行骨架提取的方法［8～10］，其中心思想是先对物体进行距离变换，寻找物体的局部极值点，最终形成骨架。这种方法提取的骨架的位置的准确性得到了保证，但是提取的点一般是离散的，很难保证提取骨架的连通性；基于Voronoi图的骨架提取方法［11］，其中心思想是利用Voronoi图来获得物体的骨架。这种方法提取到的骨架趋近于中轴，但是该算法的整体复杂性难以预料，并且对于如何处理非中轴部分也是比较复杂的；利用点云进行骨架提取的方法［12］，其中心思想是利用点云中区域内的连通性和区域间的相关性进行骨架的提取。这种方法提取的骨架的原有的拓扑结构得到了保持，但是此类方法的计算较复杂。

A*（A star）算法是一种经典的求解最短路径的搜索方法，其中心思想是利用目前已知的信息，根据目标的初始状态，当前状态以及目标状态来搜索路径。A*算法常被用于器械、游戏、导航、无人机等领域的路径规划工作。

针对部分传统骨架提取方法提取骨架位置偏离中轴的问题，提出了一种基于距离变换的A*搜索骨架的提取方法。该方法提出通过物体得到的距离场和形态学分水岭算法获得包含有物体骨架的骨架潜在图，然后通过主动轮廓线模型及物体顶点到物体凸包的距离得到对物体形状信息贡献较大的骨架端点，并将其视为骨架关键点；根据分水岭算法得到的潜在骨架图和骨架关键点，利用A*算法来搜索出物体的骨架线。该方法得到的骨架既避免了骨架的离散性问题，又保证了骨架的单像素性，对边界噪声具有一定的抗敏性。通过控制顶点到目标凸包边界的距离进行筛选，得到对目标形状有不同贡献的骨架关键点，实现骨架的多尺度控制，并且最终的骨架长度与传统的骨架提取算法相比，更接近于目标的长度。

2 骨架特征分析

2.1 距离变换

距离变换是一种图像变换的方法，会将二值图像转换成灰度图像，其中，图像中越靠近“脊”的点表示这个点距离物体的边界（零点）越远。其核心思想是根据一定的距离定义方法确定从一个点到物体边界点的最小距离。根据最小距离值的大小，给予点对应的像素值，所有的点及其对应的距离值构成对应的距离场。根据不同的距离定义，可以将距离变换划分为：非欧氏距离变换和欧氏距离变换。

关于骨架的定义有两种：一种是火烧模型；另一种是最大圆盘模型。因此，骨架是从对象内部到边界的距离最小的点集。由此可知，通过距离变换得到的距离场中的“脊”可以很好地反映这一特性，通过距离变换得到距离场，进而得到骨架的相关信息。本文利用欧氏距离变换得到的距离场。

2.2 形态学分水岭算法

形态学分水岭算法是一种传统的用于图像分割的形态学方法，其基本思想是假设在每个区域的最低点打一个洞，让水通过这些洞以均匀的速率进入每个区域，自下往上的淹没每个区域。当每个区域的水平面逐渐上升时，通过修建一个分水岭来阻止这些水平面的汇集。当在水平面上只能看到分水岭的顶部的时候，这些分水岭的顶部（由单像素构成）就相当于是分水岭分割算法中的分割线，也叫分水线。因此，这些分水线是由分水岭分割算法得到的连通的分割线。

距离场中的物体边界相当于是分水岭分割算法中的区域最低点，距离场中的高亮部分相当于是其中的“分水岭”，分水线是“分水岭”极值点的集合，而骨架是距离场中高亮部分的极值点，即分水线相当于是距离场中的骨架。

2.3 潜在骨架图

从图1（b）中可以看出，距离场中较亮的部分处于原图物体中的中间位置，且其构成的拓扑结构与原物体相似，具备了原物体大致的骨架形态。在提取潜在骨架图的步骤中，将距离场中的“脊”看作是图像分割中的“物体边界”，利用形态学分水岭算法对距离场进行“分割”，进而得到潜在骨架图。从图中1（c）可以看出，物体的骨架已经在骨架潜在图中有了体现。

图1 潜在骨架图

3 骨架端点的确定

关于端点的定义，广义上，所有的物体边界点都可以看作是端点，而关于骨架的端点，所有的物体边界凸点都可以看作是物体骨架的端点［13］，所以可以通过找到所有的物体边界上的凸点，进而确定物体骨架的端点。因此，本文利用主动轮廓线模型确定骨架端点的候选点，并根据这些点到目标凸包边界的最短距离选择不同尺度的骨架端点，从而在克服一定边界噪声的同时控制骨架尺度。

主动轮廓线模型常用来进行图像分割，主动轮廓线模型的基本原理是：首先给定一个大致的轮廓曲线，然后以给定的轮廓曲线为模板，通过调整轮廓曲线使其更贴近目标轮廓。给定的轮廓曲线是可以通过调整参数来改变的参数曲线，曲线具有相应的能量函数。能量函数不仅有表示外部能量，即图像本身的整体轮廓信息的部分，还有表示内部能量，即给定轮廓曲线的形状信息的部分。通过控制参数曲线，达到目标能量函数最小的目的。此时，得到的曲线就是目标轮廓线。虽然主动轮线廓模型在调整过程中容易陷入局部极值，不能陷入轮廓深度凹陷部分，但不影响目标边界凸点的确定。

确定目标边界的凸点后，将原始图像看作二维平面上的一组点，得到目标的凸包。利用目标边界凸点到凸包边界的最短距离，通过中心极限定理，对选定的点进行筛选，得到骨架端点。得到骨架端点之后，通过调整距离阈值d，利用物体边界凸点到凸包边界的最短距离di对骨架端点进行筛选，其中：

其中，0≤p≤1，若

则di所对应的端点候选点为筛选之后的骨架端点。这样，可以得到不同尺度的物体骨架端点，进而得到不同尺度的物体骨架。

4 基于A*搜索算法的骨架提取

得到的骨架潜在图相当于是路径搜索过程中的地图，骨架端点相当于是起点和终点。地图中，有不通的路，有障碍，若要搜索路径，A*算法在这方面表现较好。

4.1 算法流程图

本文提出的基于距离变换的A*搜索骨架提取方法的具体流程如图2所示。

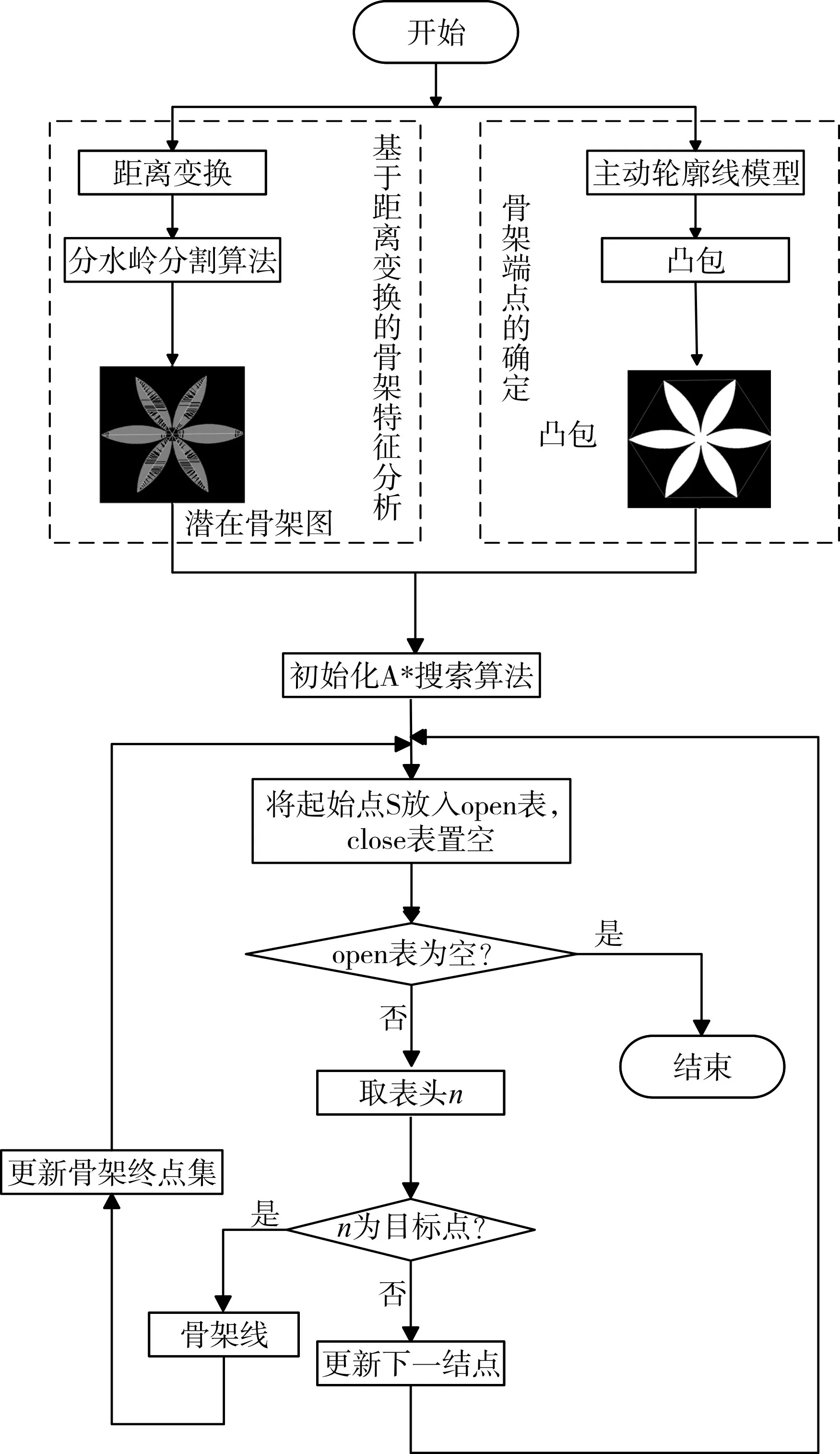
图2 本文算法流程图

4.2 A*算法的基本原理

A*算法是一种用于静态路网中求解最短路径有效的搜索方法，常用于路径规划。相较于其他的路径搜索算法，A*算法相对灵活，能用于多种多样的情形之中。在一定条件下，A*算法具有与Dijks⁃tra算法一样的功能，可用于搜索最短路径；在某些条件下，A*算法也可以和BFS（最佳优先搜索算法）一样快，此时搜索到的路径不一定是最短的，但是时间上有很大的优势。原因在于，A*算法中会有一个启发式函数用于预估代价，A*算法在路径搜索的过程中会综合考虑从初始状态到当前状态的代价和从当前状态到目标状态的预估代价。A*算法可以表示为

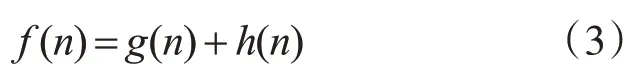
其中，g（n）代表从初始状态到当前状态的代价，h（n）代表从当前状态到目标状态的预估代价。在路径搜索过程中，A*算法会权衡两者，使f（n）的值最小。在f（n）中，g（n）的值是可知的，故启发式函数h（n）可以控制A*的行为，其中，存在两种极端的情况：若h（n）=0，即f（n）=g（n），只有g（n）起作用，此时A*算法等价于Dijkstra算法，可以保证能找到最短路径；若h（n）>>g（n），只有h（n）起作用，此时A*算法等价于BFS（最佳优先搜索算法）算法。所以，通过调整g（n）和h（n），可以得到符合要求的路径。

4.3 结点的选择和地图的构成

已经确定的骨架端点构成了A*算法中的结点集，其中，选定一个结点作为初始结点，剩余结点构成目标结点集。原图的潜在骨架图构成了A*算法中的地图，像素点被视为网格，其中，白色的部分视为可通路径，黑色部分则视为障碍。如果找到初始结点到某一目标结点的路径，则搜索成功，保存该路径且在目标结点集中删除该目标结点重新设置A*算法的目标结点集，即搜索到的路径为一骨架分支；如果找不到初始结点到某一目标结点的路径，则搜索失败，在目标结点集中删除该目标结点重新设置A*算法的目标结点集。

4.4 代价函数和启发式函数的设置

A*算法的搜索过程不是静态的，可以建立一个启发式函数，假定通过一个网格空间的最小代价是1，可以建立代价函数用于测量：

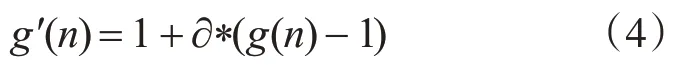
若∂=0，则改进后的代价函数的值恒为1，这种情况下，A*算法变成简单地判断一个网格可否通过；若∂=1，则最初的代价函数将起作用。

A*算法在搜索过程中，会扩展结点进行搜索，当启发式函数精确地等于实际最佳路径时，A*算法的扩展结点将会非常少。在网格地图中，有很多启发式函数，例如欧氏距离、城市街区距离、棋盘距离等，本文启发式函数中采用的是城市街区距离，故：

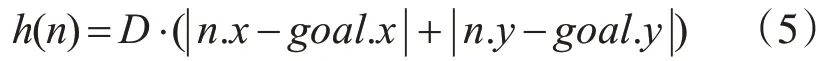
其中，D代表从一个位置移动到邻近位置的最小代价。

5 实验结果与分析

5.1 实验数据集及参数设置

实验采用的是MPEG—7 CE Shape-1 Part B数据集中的图像。关于实验中的参数设置，式（4）中∂值设置为0.5，故通过式（4）可得到：

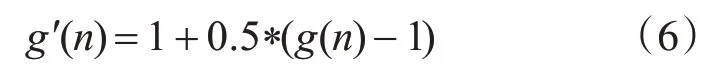
式（5）中D值设置为1，故通过式（5）可得到：

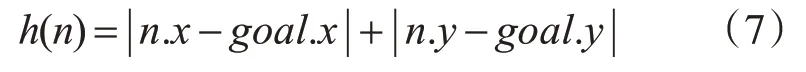
5.2 连通性和单像素性分析

本文提取的骨架是直接在得到的骨架潜在图中提取出来的，骨架潜在图是由通过形态学分水岭分割算法作用在物体的距离场上得到的分水线构成。通过形态学分水岭分割算法得到的分水线具有连通性和单像素性，故骨架潜在图中的骨架具有连通性和单像素性，由此可知，最后得到的物体骨架具有连通性和单像素性。如图3所示，本文的方法得到的骨架有较好的连通性。

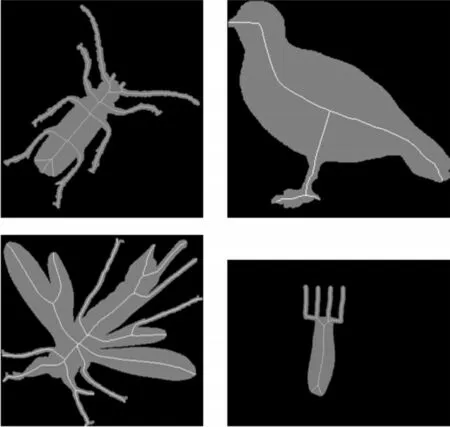
图3 一些二值图像的骨架

5.3 多尺度控制变化分析

通过主动轮廓线模型得到物体骨架端点候选点之后，通过调整p值，控制阈值大小，进而得到不同尺度的骨架端点。图4所示是本文算法通过调整参数得到的不同尺度的物体骨架。从图中可以看出，本文算法通过调整参数得到了三种不同的骨架尺度，具有一定的骨架尺度控制能力。

图4 同一物体不同尺度的骨架

5.4 骨架长度分析

本文算法得到的骨架是通过对物体的距离场图进行分水岭分割算法得到的，得到的骨架长度相较于其他算法，更接近于物体的长度。图5、图6所示是本文算法和Yu等［14］方法、Choi等［15］方法的实验结果对比，其中，图5（a）、图6（a）为本文算法实验结果，图5（b）、图6（b）为Yu方法实验结果，图5（c）、图6（c）为Choi方法实验结果。从图5中可以看出，本文算法和Yu方法实验结果的骨架长度相较于Choi方法实验结果的骨架长度更接近于物体的长度；Yu方法得到的骨架在锤子弯曲的地方有冗余的骨架分支（白色圆圈内）。从图6可以看出，本文算法与Yu方法实验结果的骨架长度相较于Choi方法实验结果的骨架长度更接近于物体的长度；本文方法与Yu方法的对比：钥匙柄处是上下对称的，上方两条骨架分支的交点与下方两条骨架的交点（或左方两条骨架分支的交点与右方两条骨架分支的交点）应该在同一垂直线（或水平线）上。这一点，本文方法表现比Yu方法好。

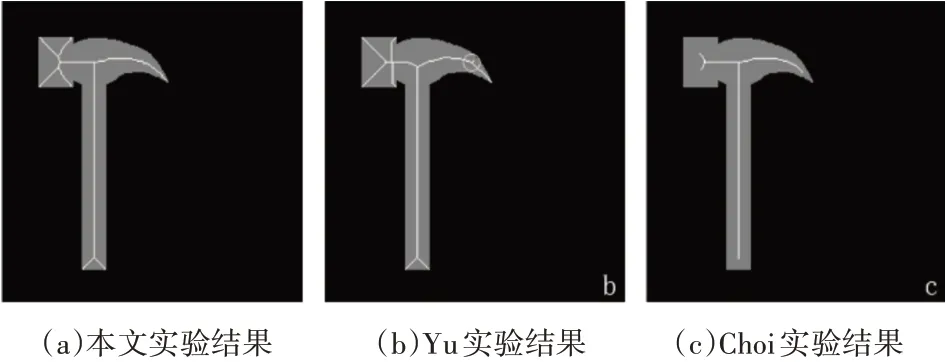
图5 实验结果对比图一

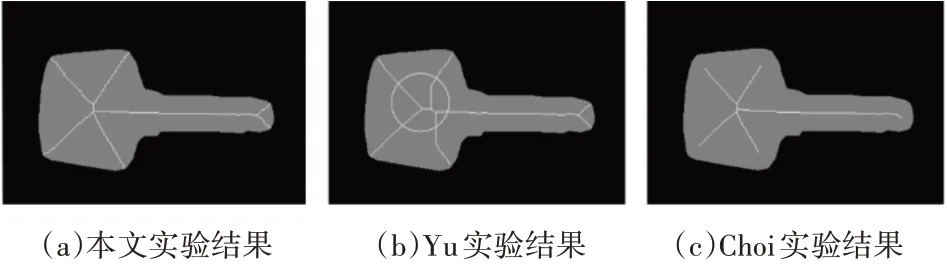
图6 实验结果对比图二

5.5 边界噪声

本文算法利用距离变换得到的距离场，进行分水岭分割，以及利用对噪声不敏感的主动轮廓线模型来确定骨架的端点，在一定程度上克服了一定的边界噪声的影响。图7、图8比较了在有无边界噪声情况下，本文算法的表现。由图可以看出，有噪声时，得到的物体骨架在细微处会有些变化，但从整体上看，得到的物体骨架仍然可以表示物体的拓扑结构。

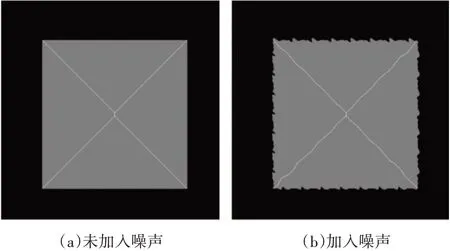
图7 边界噪声分析图一

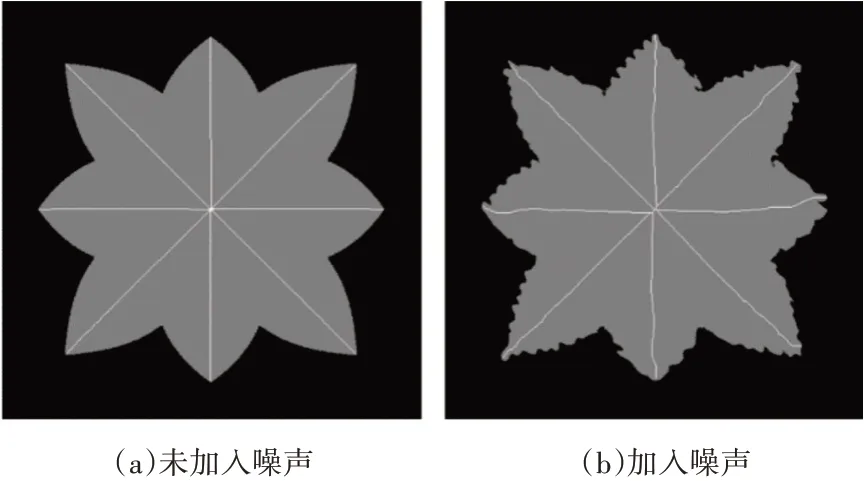
图8 边界噪声分析图二

5.6 物体骨架的拓扑结构分析

骨架常被用来进行物体识别，所以提取的物体骨架是否能正确的表示物体的拓扑结构至关重要。图9比较了本文算法和Yu方法的实验结果，其中，图9（a）是本文算法的实验结果，图9（b）是Yu方法的实验结果。由图可以看出，物体边界有一处较为凸起的部分（白色圆圈内），图9（a）相较于图9（b）在此处多了一条骨架分支，加上这条骨架分支，更能很好的表示物体的拓扑结构。图10是本文算法对两个形状相似的物体的实验结果。图10（a）和图10（b）之间的差别在于，图10（b）的边界不是直线，而是向物体内部凹陷的曲线。由图可以看出，两个实验结果在底边处有明显的差别（白色圆圈内），图10（a）此处的骨架趋近于水平直线，图10（b）此处的骨架向物体内部凹陷。

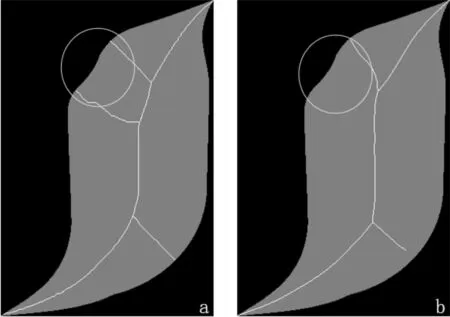
图9 拓扑结构分析图一

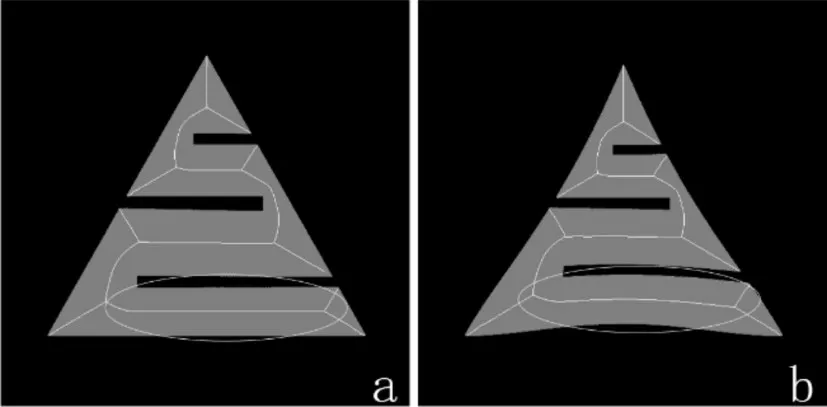
图10 拓扑结构分析图二

6 结语

针对部分传统骨架提取方法提取骨架位置偏离中轴的问题，提出了一种基于距离变换的A*搜索骨架的提取方法。该方法利用距离场和形态学分水岭算法获得包含有物体骨架的骨架潜在图；利用主动轮廓线模型确定物体凸点，通过物体顶点到物体凸包的距离，对骨架凸点进行筛选，得到骨架关键点；利用A*算法对多个目标点进行搜索，进行骨架修剪，得到骨架。实验结果表明，该方法获得的骨架具有连通性、单像素性、一定的抗噪能力等优点。