基于多维分段和动态权重DTW的多元时间序列相似性度量方法*
2021-12-01魏国强周从华
魏国强 周从华 张 婷
(1.江苏大学计算机科学与通信工程学院 镇江 212013)(2.无锡市妇幼保健院 无锡214002)
1 引言
在我们的生活中,诸如金融、医疗和气象等领域产生的具有一定时间先后性的数据可称为时间序列数据[1]。随着信息时代的到来,现代科学技术水平不断提高,各个领域产生的时间序列数据也不断增加,如何从海量的时间序列数据中发掘出隐含的深层知识成为一个热点问题。时间序列数据挖掘就是利用数据挖掘技术从时间序列数据中发现潜在的有价值的信息和模式,它也已成为目前数据挖掘领域中十个最具挑战性的问题之一[2]。
时间序列是指在一段时间内,以相同的时间间隔对某个潜在的过程观测并采样得到的一系列观测值,根据同一时间采集的数据指标个数不同可以将时间序列分为一元时间序列可多元时间序列。与一元时间序列相比,多元时间序列在现实生活中更为常见,例如,天气数据可以用最高温、最低温、空气湿度和降水量等变量来描述[3],医学中患者的身体状况也可以通过一系列生理指标的变化反映出来。
基本的时间序列数据挖掘方法包括聚类、分类和相似性搜索等,而这些方法首先都需要比较时间序列的相似性,即相似性度量。相似性度量也是时间序列数据挖掘的关键技术之一,其结果直接影响了时间序列数据挖掘的效果[4]。然而,目前的时间序列相似性度量方法大多面向一元时间序列,对多元时间序列的研究相对较少,还未形成一个系统的体系[5]。多元时间序列的多个变量之间存在某种相关性,共同影响了系统的状态和发展趋势,因此并不能视为一元时间序列的简单叠加[4],目前的一元时间序列相似性度量方法也不能直接用于多元时间序列。因此,研究多元时间序列相似性度量具有重要的理论和现实意义。
多元时间序列由一系列时间点数据构成,其时间跨度和时间间隔决定了序列的时间维度。若直接在维度高的原始数据上进行相似性度量,不仅计算量大,运行效率低,数据的噪声和冗余也会对度量精度带来较大影响。因此,参照普遍的机器学习和数据挖掘方法,首先需要对多元时间序列进行特征提取,保留有价值的信息并降低数据维度。同时,多元时间序列的复杂性也源自其多元性[6],其变量个数决定了序列的变量维度。由于变量之间存在相关性,在进行模式表示时不仅要降低序列维度,还要考虑变量之间的相关性。
SVD方法[7]是一种基于主成分分析方法的多元时间序列模式表示方法,该方法将原始高维数据映射到低维空间,搜索出若干最能代表数据的k维正交向量,使原始数据被投影到较小的空间中。文献[8]提出一种基于点分布特征的方法PD,通过三维空间描述多维时间序列,提取极大值、极小值等9个局部重要特征点对原始序列进行模式表示。这两种方法都是基于统计的模式表示方法,忽略了变量之间的相关性关系,同时都有一定的局限性,例如前者需要有足够的样本点,后者对数据规模较小且样本形状差异大的数据才比较有效。文献[9]提出一种趋势距离TD,对多元时间序列进行多维分段拟合后,选取拟合多项式的一次项系数和拟合段的时间跨度作为序列特征,并基于DTW距离进行时间序列的相似性度量。在多数数据集上,该方法都能取得较高的度量精度,但在一些序列较短,形态变化不突出的数据集上,得不到理想的度量效果。
在对多元时间序列进行模式表示之后,需要设计相应的距离度量函数衡量序列特征之间的相似程度。目前较常用的相似性度量方法有欧式距离[10]和动态时间弯曲(DTW)[11]距离。欧式距离简洁明了,易于理解和计算,但仅能实现序列之前“一对一”的匹配方式,因此需要满足序列长度相等的前提条件。与欧式距离相比,DTW距离支持序列在时间轴上的伸缩与弯曲,允许两条序列拥有不同的长度,但可能存在畸形匹配。对此,文献[12]提出一种自适应窗口法,通过对数据的学习,自适应地限制最佳弯曲路径的搜索范围;文献[13]提出加权动态时间弯曲距离(WDTW),在求解时引入权重参数,来控制弯曲路径偏离对角线的程度。但以上两种方法都在原始DTW的基础上引入外在的参数,如何设置这些参数成为另一个复杂的问题。
针对现有的特征表示算法存在的问题,本文基于多维分段的序列分段方法,选取拟合线段的斜率、均值和时间跨度作为特征模式。针对动态时间弯曲距离的畸形匹配问题,提出一种动态权重动态时间弯曲距离(Dynamic Weighted Dynamic Time Warp,DWDTW),在搜索最佳弯曲路径的过程中,为每个拟合段动态地赋予权重,拟合段的匹配次数越多,权重越小,通过限制拟合段匹配次数来解决畸形匹配问题。使用DWDTW距离度量提取到的多元时间序列特征矩阵之间的相似性,提出了一种基于多维分段和DWDTW的多元时间序列相似性度量方法(简称MS-DWDTW),并通过实验证明了该方法的准确性和适用性。
2 多元时间序列模式表示和特征提取
一条多元时间序列可以用X=(X1,X2,…XT)表示,而Xt=(x1(t),x2(t),…xm(t)),其m为变量个数,T为时间点数量,xi(t)(1≤t≤T,1≤i≤m)表示第i个变量在第t个时间点的观察值。
对多元时间序列进行模式表示,较为常用且直观的方法是分段线性拟合(PLR),即在每个变量维度上将时间序列分段,并采用每一段的均值来表示该分段,构成该多元时间序列在该变量维度上特征。最后将每个变量维度上获得的特征依次排列构成多元时间序列特征向量,即将多元问题转化为一元问题[9]。然而,多元时间序列具有时间和变量两个维度,这种做法只考虑时间维度而忽视了变量维度。多元时间序列各个变量之间往往存在一定的联系,某个时刻某个变量维度中出现的特征在其他相关的变量维度也会有所体现。
多维分段是指在进行分段拟合时,在所有变量维度上同时进行分段,在降维的同时也保留了变量之间的关联关系。例如,在人体行走时,左膝高度和右膝高度是两个相关的变量,图1(a)和图1(b)分别是对一个连续的行走动作进行单维分段和多维分段后的结果[9]。可以看出,由于数据误差的存在,多维分段的意义要远大于单维分段。
文献[9]使用多维分段的分段方式,采用每一段的趋势和时间跨度来进行特征表示。但是,基于趋势和时间跨度的特征表示只关注分段上的趋势信息,丢失了分段的值域信息,若两条序列的趋势基本相同但值信息差别很大,这种特征表示方法并不能体现出两条序列之间的差异性。基于此,本文将分段均值信息加入到分段特征中,将多元时间序列的趋势和均值信息作为序列特征。
在多维分段之后,在所有变量维度上,均选择对应拟合多项式的一次项系数k,分段均值a和分段时间跨度l作为分段特征。若具有m个维度的多元序列被分成S段时,该序列可用如下m×S的矩阵表示:
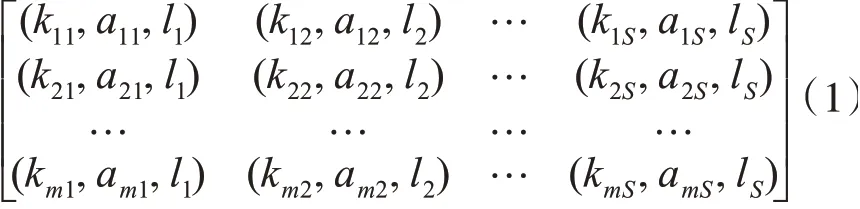
针对多元时间序列,考虑到变量之间的差异性,尤其是在量纲上变量之间的差异可能表现得特别突出,需要对提取到得特征矩阵做标准化处理,本文对三个特征分别做如式(2)~(4)所示的处理:
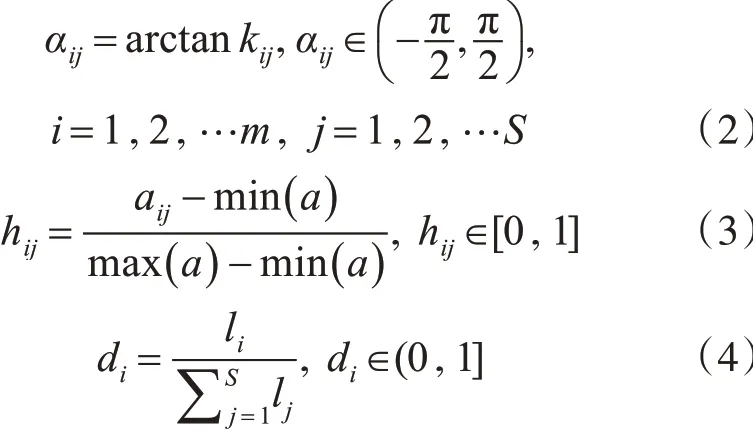
标准化处理之后,得到的转换后的特征矩阵如下所示。
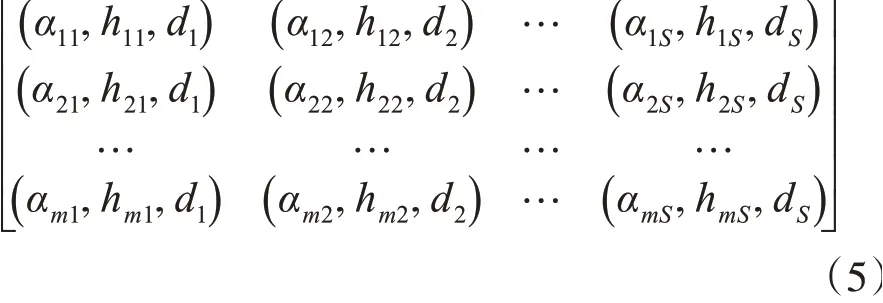
3 基于动态权重的动态时间弯曲距离
度量多元时间序列之间的相似性,实质上是比较提取到的特征矩阵之间的相似性。由于同一数据集下所有多元时间序列具有相同的变量个数,所以特征矩阵的行数是相同的;但不同序列的分段可能不同,所以矩阵的列数一般差别不一,因此需要能用于不同列数的特征矩阵之间比较的距离度量方法。
特征矩阵可以看作原始多元时间序列在多维分段之后的特征序列,矩阵的列数不同即序列的长短不一。动态时间弯曲距离(DTW)能通过对时间轴的弯曲解决两个不同长度序列之间相似性度量的问题,因此可以用于特征矩阵之间的比较。而原始的DTW在计算最佳路径的同时,可能会因为追求累计距离最小化而将某一序列上的一个点对应到另一序列上的多个点上,继而带来畸形匹配问题。
畸形匹配会因为时间序列被严重压缩而丢失序列特征,对原始时间序列距离的度量也就变得不再准确,若在得到多元时间序列序列特征矩阵(5)之后直接使用原始DTW进行距离度量,也不可避免地会遇到畸形匹配的问题。基于此,本文提出一种动态权重动态时间弯曲距离,该方法为每个序列点赋予权值,在动态规划求解最佳弯曲路径的过程中,动态地调整每个点的权值,一个序列点被匹配的次数越多,其权值也就越小,与其他点的匹配距离就越大,被再次匹配的可能性就越小。
经过标准化处理得到的的特征矩阵(5),可以进一步简化表示为X=[x1,x2,x3…xS],其中xi指多维分段后第i个分段区间包含的m个变量的特征值,可以将其当作一条序列上的第i个序列点。两条序列X和Y中的两个序列点xi,yj之间的基础DTW距离可以定义为
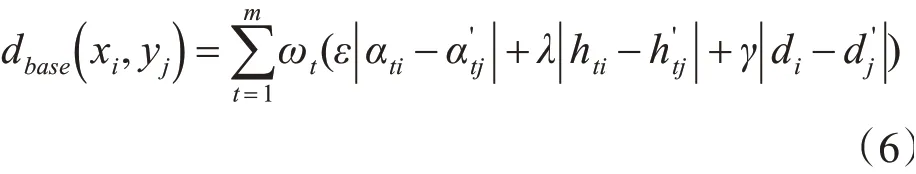
它体现了X和Y在第i段拟合和第j段拟合上所有变量维度的累计差异。由于多元时间序列不同维度代表的实际意义不同,对累计差异的贡献度也存在差异,因此需要为每个变量赋予一定的权重。在式(6)中,使用ωt表示第t个变量所分配的权重值,且ωt的值满足式(7):分别表示两个拟

合段xi和yj在第t个变量上趋势、均值和时间跨度上的差异性,ε、λ和γ则分别代表三者差异的权重值,同时有下式成立:

在DWDTW距离中,第i个拟合段的权重定义如下:
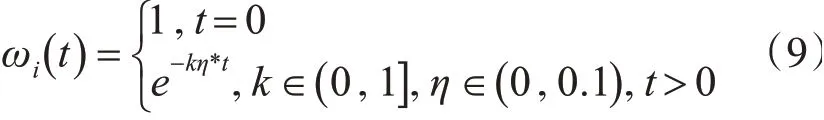
其中,t表示了拟合段在求解过程中被匹配的次数,拟合段的初始权重为1,被匹配的次数越多,即t越大,拟合段的权重ωi(t)越小。为了防止权重衰减过快,引入权重衰减系数η,η越大,权重衰减越快,其取值在( 0 ,0.1)区间内,通常取0.05。同时,考虑到当两条序列长度不同,特别是长度差异较为明显时,势必会有短序列上一个点对应长序列上多个点的情况,此时不应被判定为畸形匹配,对长序列上的点应给予较大的多次匹配宽容度。因此,引入序列的长度比值k,其定义如下:
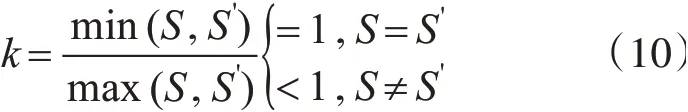
S和S'分别代表特征表示之后两条序列的长度。当两条序列的长度差异越明显即k越小时,权重ωi(t)的减小速率也越小,宽容度也越大。
从式(9)可看出,拟合段的权重是在计算过程中自行确定且动态缩小的,其值仅与两个序列的长度比和拟合段被匹配的次数有关,无需人为设定。引入动态权重信息后,两条多元时间序列之间的DWDTW距离可以使用动态规划的方法计算:
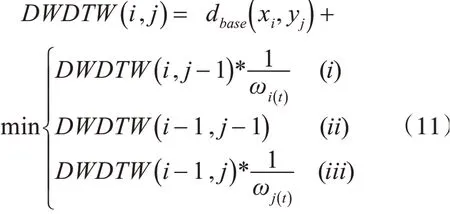
其中,DWDTW(i,j)表示第i个拟合段和第j个拟合段之间的DWDTW距离,DWDTW(1,1)=dbase(x1,y1)。ωi(t)表示了第i个拟合段当前的权重,式(i)表示在计算经过(i,j-1)→(i,j)的路径的弯曲距离时,拟合段i被重复使用,因此需要在原距离基础上乘以,增大该路径的距离,以限制算法对其的选择;同时,若最终算法依然选中该路径,即式(11)选中式(i),需要调整第i段的权值,进一步减小其权重。最终,DWDTW算法的描述如下。

4 实验
4.1 实验环境
软件环境:Python3.6.0+Windows10操作系统
硬件环境:处理器Intel Core i5-3337U,内存8Gb,硬盘容量500Gb。
4.2 实验数据
实验使用的多元时间序列数据来自UCI数据集。其中,ASL[14]数据集记录了来自5名手语采集者共95个语意的手语信号信息,每条序列包含22个连续变量,每个语意有27条序列。本文选择了前10种 语 意(alive,all,answer,boy,building,buy,change(mind),cold,come,computer)共270个序列,序列长度不等且在47~95之间。REF[15]数据集是监控机械故障得到的数据集,包含了5个子数据集,数据分为4类,每个序列包含6个变量,序列长度为15,本文选择了LP1数据子集共88条序列进行实验。EEG[16]是由脑电图像数据构成的数据集,实验选取了alcoholic和control两类数据,包含64个变量,序列长度256。本文选取编号为a_co2a0000364和c_co2c0000337的两人各10次测试作为实验数据,共20个多元时间序列。JV(Japa⁃nese Vowel)[17]记录了日语元音的发音过程,序列长度在7~29之间,属于多数算法表现都不理想的小规模的多元时间序列。
4.3 实验结果及分析
在DTW距离度量中,数据点之间的基础距离对度量结果产生直接的影响。在式(6)中,基础距离的计算结果同样会受到ε,λ,γ三者组合的影响,并最终影响到序列直接的距离计算结果。因此,本文首先介绍基于ASL数据集使用KNN分类确定最优参数的过程。文中选取K为10,即从测试集中寻找与测试序列的MS-DWDTW距离最小的10个序列,计算结果的查准率,查准率定义为

针对每种组合,分别使用10条不同的输入序列,并计算平均查准率。为了不失一般性,这里为每个变量取相同的权重ωt,权重衰减速率η取值0.05。实验结果如表1所示。注意,由于三者的和为1,表中γ的值并未直接给出。例如当ε=0.0,λ=0.0时,则有γ=1.0。
从表1可知,当ε=0.7,λ=0.2,γ=0.1时,取得最大的平均查准率0.94。可以注意到,在拟合段斜率分配了较小权重即ε取值较低的情况下,随着均值差异权重λ的增大,平均查准率也在不断增大,说明当趋势特征差异不大时,序列的均值差异将主要影响度量结果。同时可以观察到,表中第一列的数值均小于相应行上的其他列,同样表明距离度量过程中引入的均值差异能够提高度量精度,说明了其不可或缺的重要性。
下面基于MS-DWDTW方法在选取的不同特性的数据集上进行相似性比较,以验证其准确性。本文在选取的数据集上对比了基于MS-DWDTW与MS-DTW、DTW、PD、TD和SVD的KNN算法在进行相似性查找时的查准率。其中,DTW方法直接使用原始数据和动态时间弯曲距离进行相似性度量,MS-DTW表示对原始数据采用本文的方法进行特征提取之后,使用原始DTW计算特征矩阵之间的距离。为了使实验结果更具比较性和说服力,本文利用得到表1的实验方法在每个数据集上确定表现最好的参数组合,参数选择结果见表6。每种方法分别取与测试数据集中数据距离最小的1、5、10条序列,计算最终的平均查准率,实验结果见表2~表5。
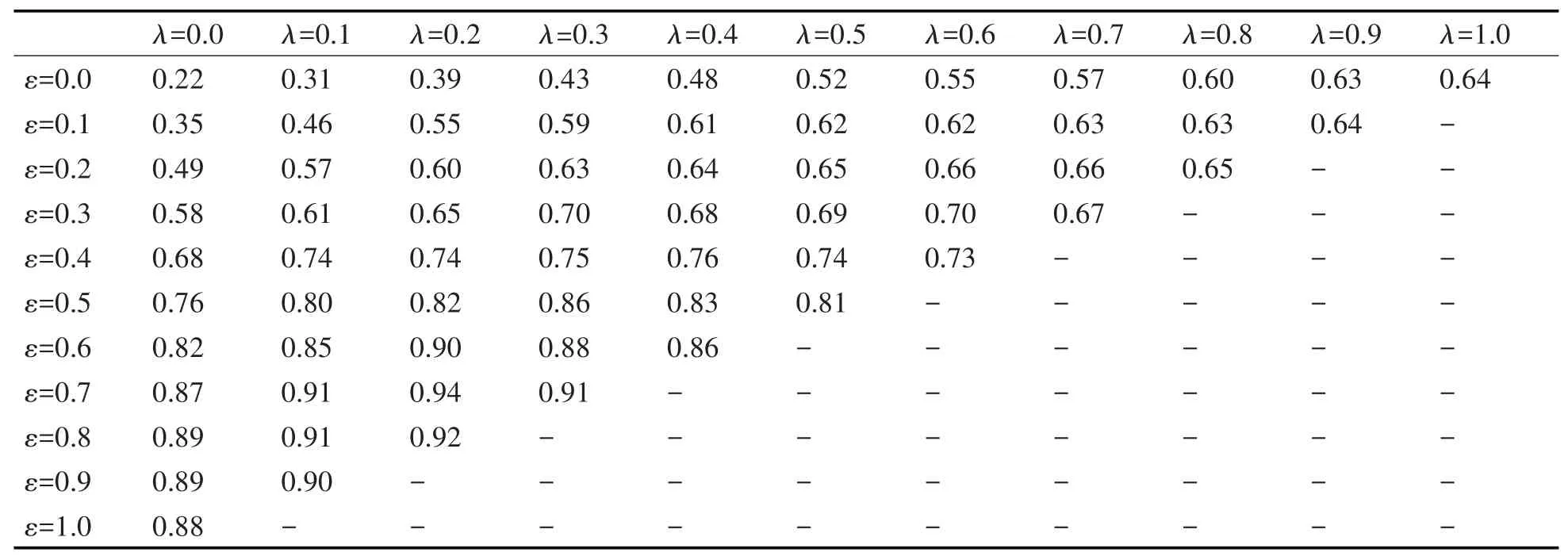
表1 ASL数据集不同的ε,λ,γ选择下的平均查准率
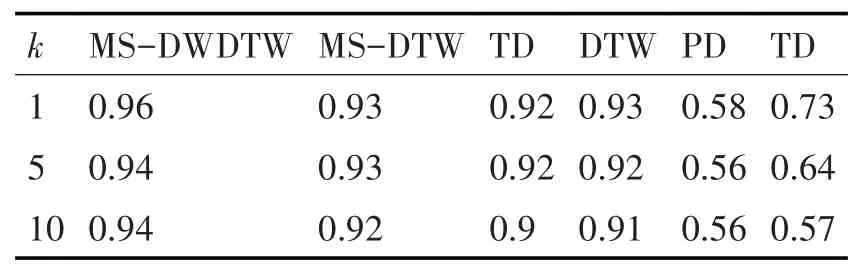
表2 ASL数据集实验结果
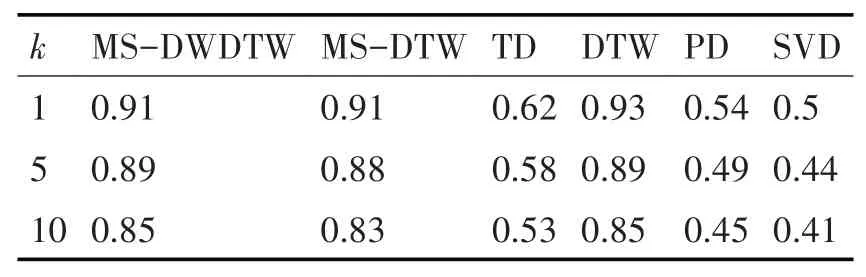
表5 JV数据集实验结果
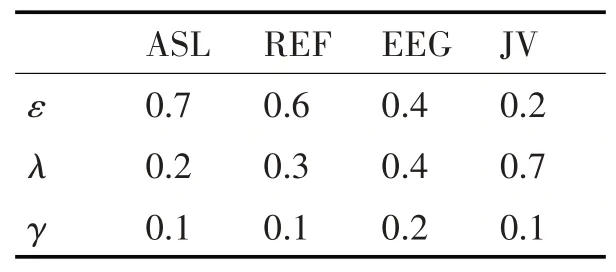
表6 不同数据集下ε,λ,γ选择情况
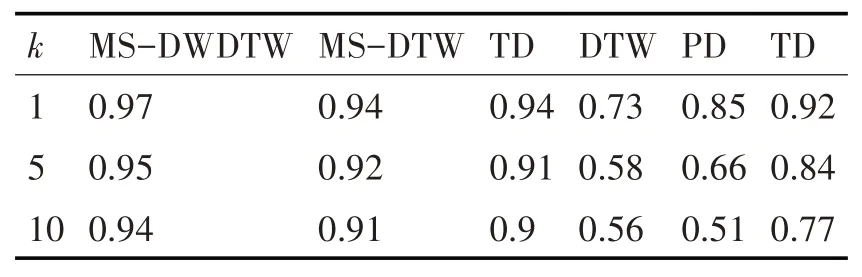
表3 EEG数据集实验结果
由表2~表5可知,基于MS-DWDTW的KNN算法在四个数据集上均能取得较好的平均查准率。在ASL和EEG数据集上,MS-DWDTW的平均查准率均为最高,MS-DTW和TD也能取得不错的结果。但进一步对比发现,由于MS-DTW加入了均值信息作为序列特征,其结果要优于TD方法。同时,相比于MS-DTW,MS-DWDTW的平均查准率得到一定程度的提高,由此可知,在这两个数据集上基于DTW算法的相似性度量出现了畸形匹配的情况,且对度量精度产生了一定的影响,而引入动态权重后有效改善了该问题。
此外,在EFG和JV两个数据集上,MSDWDTW也取得了较好的结果,但从表4和表5可以看出,MS-DWDTW与MS-DTW的结果相差不大,说明序列的畸形匹配并不严重。同时,可以观察到,TD算法在JV数据集上取得了较低的平均查准率,原因在于JV数据集序列较短且趋势变化不明显,针对此类数据集,其已经丧失有效性,而MS-DWDTW仍能通过增大均值权重减小趋势权重的方法取得较为准确的结果。
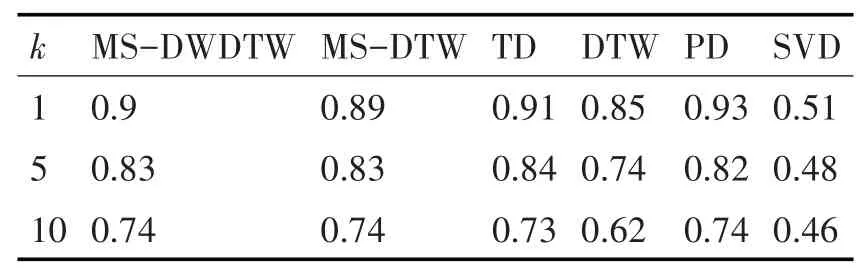
表4 REF数据集实验结果
5 结语
本文提出的基于多维分段和动态权重DTW的多元时间序列相似性度量方法,在各个变量维度上统一分段,保证了分段之后变量之间的相关性,选取分段后拟合线段的斜率、均值和时间跨度作为多元时间序列的特征表示,能比较准确描述多元时间序列的趋势和值特征。本文提出的DWDTW距离度量也能在不增加额外参数的情况下有效避免传统DTW距离的畸形匹配问题,进一步提高多元时间序列距离度量的准确度。实验结果表明,MS-DWDTW能在多个数据集上取得较好的度量效果,同时能够通过调整最优参数来适应多种类型的数据。但是,MS-DWDTW的参数较多,模型参数优化较为复杂。接下来的工作主要是研究如何优化模型参数选择方法,并将MS-DWDTW方法用在多元时间序列数据挖掘任务如聚类、分类中去。
