基于近场声全息的重建算法分析与研究
2021-11-30郭世旭王月兵郑慧峰徐遨璇
陈 璐, 郭世旭, 王月兵, 郑慧峰, 徐遨璇
(中国计量大学 计量测试工程学院, 浙江 杭州 310018)
1 引 言
近场声全息(near-field acoustical holography,NAH)是声学研究中的一种极其重要的声场推算方法,由Williams提出并根据空间声场变换进行大量实验应用[1~3]。近场声全息技术在噪声源定位、声场重构及可视化方面有重要应用。通过在辐射体的近场区域内测量声场数据重建和预测整个三维空间的声学特性,从而识别和定位声源,获得声源的声辐射特性,达到判断噪声来源进行声源控制的目的。目前工程中基于近场声全息的噪声分析识别算法主要包括空间声场变换声全息(spatial transformation of sound field,STSF),统计最优声全息(statistically optimized NAH,SONAH),等效源法声全息(equivalent source model,ESM)等算法。在算法的选择和应用上,需要根据实际需求以及应用场合进行选取。
在技术研究方面,首先兴起的是STSF,Arteaga通过对全息声场数据进行线性预测边界填充外推法,使STSF算法可在较小孔径下仍具有理想的重建精度[4]。姬庆对比了不同格林函数对声场重建的影响[5]。Jiang等通过结合正交球面波叠加法和数据扩展法来改进算法,提高声场重构的精度[6]。郭世旭结合二维平面声压构建技术提出了高效率的声场测量方法[7]。由于重建非稳态声场的需求,基于等效源的近场声全息算法受到重视,Pereira在球型阵列的等效源法中引入权矩阵对函数进行迭代求解,达到了提高低频近场重建精度的目的[8]。王成利用等效源算法对高频换能器声场进行有效分析[9]。陶文俊提出了一种用压缩感知将声强信息转为稀疏信号的方法,进而优化该算法[10]。陈汉涛运用经验模态分解法与等效源法结合,使低信噪比条件下的弱声源得以检测[11]。统计最优算法研究起步最晚,张永斌提出了一种平面波优化方法,对传递函数进行改进,提升了重建精度[12]。赵报川通过多种波函数组合得到声场传递函数提高了声场重建的精度[13,14]。熊久鹏提出二维平面声压重构技术来提高声场测量效率[15]。
在实际测量中,近场声全息算法的精度受多方面影响,主要有声源频率、重建距离、测量面采样间距、正则化参数选取等,本文在这些研究的基础上,将仿真和实验相结合,互相验证,分析总结各个算法受上述因素的影响规律,并对运算效率进行分析比较,为不同需求的水下近场声全息算法选择及参数选取提供了一定参考。
2 近场声全息算法原理
2.1 基于空间声场变换的声全息技术
当格林函数满足声源表面均匀边界条件时,Helmholtz方程的积分形式如下表示:
(1)
式中:x是位置矢量;r是声源和对应点所在面的法向距离;下标S表示声源面的性能评价;p表示声压。如果声源面和全息面共形,它们之间可以通过测量数据和格林函数的卷积运算得到。波数域测量面声压通过和格林函数乘积后再经由逆Fourier变换得到空间重建面声场,计算公式如下:
p(kx,ky,zS)=F-1(p(kx,ky,zH)e-ikz(zH-zS))
(2)
式中:kx、ky和kz分别表示在x、y和z轴方向的波数;p(kx,ky,zS)与p(kx,ky,zH)分别表示全息面与测量面的声压;zH和zS分别表示全息面和测量面与声源的距离;F-1表示傅里叶逆变换。
2.2 基于统计最优的声全息技术
基于统计最优的近场声全息技术是局部近场声全息算法的一种,核心算法是通过赋予空间声场的复声压权值来计算重建面的声压,自由声场里任意点的复声压都可以用多个空间声场中的传播波和倏逝波叠加计算得到:
(3)
式中:p(rH,n)为测量面上的声压。复声压权重系数C(rS)只和位置有关,即只要重建面与全息面的相对位置关系不变,不同声压都可以用同样的权重系数矩阵。用标准Tikhonov正则化求解出系数C(rS)代入式(3)即可得基于统计最优的重建面声压计算公式:
p(rs)=pT(rH)(AHA+θ2I)-1AHα(rS)
(4)
式中:H表示矩阵的共轭转置;I表示单位对角矩阵;θ表示正则化参数;A表示2个平面间的传递矩阵;α(rS)为距声源rS处平面波组成的列向量。
2.3 基于等效源的声全息技术
等效源近场声全息技术的基本思想是用辐射场内部等效源叠加替代该物体所产生的辐射场。单个等效源强度可定义为[16]:
(5)
式中:G表示自由场格林函数;q表示虚拟声源。
为避免声场重建过程中奇异值带来的误差,计算虚拟表面声强时对声源表面进行反运算,由测量面声场信息倒推出等效源后再重建出真实的重建面声场。计算公式如下所示:
pS=GVS(pH(GHV)-1)
(6)
3 正则化方法
3.1 Tikhonov正则化
将测量面的声压信息pH中的误差假设为空间不相关、方差为r2的高斯噪声εp,那么噪声和重建声压有如下关系:
pH=HpS,pH=pH0+εp, var|pH|=r2
(7)
式中:var为方差。
标准Tikhonov正则化分解通过增加一个约束项,使得求解最小二乘解的病态方程变成非病态方程。

(8)

标准Tikhonov正则化解为:
C(rs)=(AHA+θ2I)-1AHα(rS)
(9)
式中:H表示矩阵的共轭转置;I表示单位对角矩阵。
正则化参数θ有多种计算方式,主要有广义交叉验证法、L曲线法、固定参数法等,一般情况下固定参数的计算公式为[17]:
(10)
式中:d表示全息面和重建面间的距离;SNR表示信噪比。
3.2 广义交叉验证法(GCV)
GCV法的主要思想是当在声全息重建过程中缺失一个声场信息时,用此时的声场模型的正则化解预测缺失的声场信息。在标准Tikhonov正则化求解中GCV函数可以用下式表示:
(11)
式中:Tr为矩阵的迹。GCV函数达到极小值时对应的θ就是所求的正则化参数。
3.3 L-曲线法(L-curve)

(12)
式中:ρ′、ρ″、ζ=、ζ″分别为ρ和ζ的一阶、二阶导数。该函数的曲率达到极大值时对应曲线的拐角系数为正则化参数θ。
4 仿真模型及仿真结果
首先建立有限元仿真模型,声源放置于坐标原点,测量面与重构面处于z方向法线上,且平行于xy平面,两个面大小相等,见图1。声源频率设置为500 Hz,测量面距声源0.3 m,重建面距声源0.25 m,测量面和重建面的大小都为1 m×1 m,采样点数为11×11个。仿真环境为水域,声速c=1 500 m/s,水密度ρ=1 000 kg/m3,模型采用边界元,因此忽略实验环境中的水面和池壁反射,为了精确解析整个声学域的压力梯度变化,使用二次单元进行离散化处理,在进行频域仿真时,对其采用大小为λ/6的细化网格,通过有限元仿真获得测量面是理想值。
图1 声场测量示意图Fig.1 Schematic diagram of sound field measurement
4.1 声源频率对重建精度的影响
在上述有限元仿真模型的基础上进行参数调整:修改声源频率为300 Hz到1 500 Hz,分别计算3种近场声全息算法随频率变化产生的重建误差。
由图2可以看出,在低频区域(<700 Hz),ESM算法的误差低于6%,其重建精度较高;当频率大于700 Hz时,3种算法的重建误差随着频率增大而线性增大,且SONAH>ESM>STSF;同时随着频率增大,3种算法的重建精度变化趋势相对稳定。
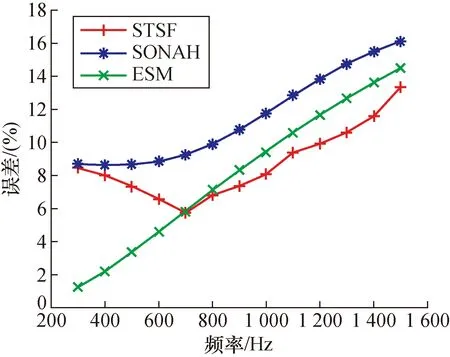
图2 误差随频率的变化曲线图Fig.2 Variation curve of error with frequency
4.2 重建距离对重建精度的影响
对部分仿真条件进行调整,声源频率为500 Hz,获取距声源0.26~0.53 m的声场数据,计算测量面与重建面距离变化时3种近场声全息算法的重建误差。
由图3可以看出,ESM与SONAH在0.3 m的范围内重建误差较小,STSF在超过0.1 m后重建误差呈指数型增长,结果发生严重失真。总体上,3个算法的重建误差都随着重建距离增大而增大,重建误差STSF>SONAH>ESM。

图3 误差随重建距离的变化曲线Fig.3 Variation curve of error with reconstruction of distance
4.3 采样点数对重建精度的影响
修改仿真条件,声源频率为500 Hz,测量面和重建面分别距声源0.3 m、0.25 m,分别以 5×5到19×19采样点数对测量声场进行采样,计算比较算法重建误差变化。
由图4可以发现,3种算法的重建误差随着采样点数的增加而减小,且STSF>SONAH>ESM。当采样点数大于250后,采样点数变化对重建精度的贡献率基本不变。其中随着采样点数的变化,ESM与STSF的误差浮动范围为10%,SONAH的误差浮动范围为25%。

图4 误差随采样点数的变化曲线Fig.4 Variation curve of error with the number of sampling points
由于算法的运算方式不同,声场数据量对计算效率的影响会有所差异。声场数据量的大小取决于采样点数,通过选取不同采样点数,对3种重建算法的重建运算时间进行计算分析。由于基于统计最优的近场声全息算法运算时间较长,因此对各算法的运算时间取对数后进行对比。由图5可以看出运算时间:STSF> ESM>SONAH。其中SONAH算法由于测量面声场信息的矩阵维度提升而大幅降低重建速度,因此在计算高维度声场且对重建速度要求不高时可选用ESM算法,当对速度有较高要求,对重建精度要求不高时可选用STSF算法。

图5 运算时间随采样点数的变化曲线Fig.5 Variation curve of operation time with the number of sampling points
5 实验与结果
5.1 实验系统搭建
为验证算法的重建效果,在开阔大型水域进行实验。实验环境水域深度足够,湖面平稳,无过往船只及人员干扰。测量系统如图6所示,阵元为相幅一致的水听器。

图6 测量系统示意图Fig.6 Schematic diagram of measurement system
水听器阵列尺寸为3 m×2.875 m,由168个水听器排列成7行24列。选用柱形换能器,高度为0.08 m,直径为0.06 m,实验中可视为点声源。固定水听器阵列,换能器与水听器阵列中心位置相对。首先激励换能器工作,在开阔水域中形成声场分布,然后利用水听器阵列对水域声场进行测量,输出信号同步呈现在示波器上,最终将数据读取并存储在电脑中。实验器材:低频换能器、功率放大器、信号源、示波器、水听器阵列、采集卡、上位机。
5.2 算法结果比较
首先从声源频率、重建距离、采样点数及正则化方式4个方面采集实验数据,然后利用各个算法进行声场重建,最后分析比较,验证仿真结果。实验环境中信噪比接近60 dB,前3者比较中皆选取Tikhonov正则化固定参数法进行重建。
为了便于算法重建效果比较,采用分贝误差定义声场重建误差:
(13)
式中:ps(m,n)和ph(m,n)分别为理论面和重建面点(m,n)处的声场信息。
5.2.1 根据频率变化的重建精度比较
将距离换能器0.05 m处的声场面作为重建理论面,距离为0.15 m处作为测量面。用换能器分别发射频率为500 Hz、1 000 Hz、2 000 Hz的声波,得到不同频率下重建面和理论面的声场信息。用STSF算法、SONAH算法与ESM算法进行声场重建,重建效果与重建误差如图7与表1所示。

图7 3种算法在不同频率下的重建效果Fig.7 The reconstruction effects of three algorithms at different frequencies

表1 不同频率下的重建误差Tab.1 The reconstruction error of each frequency dB
可以看出,在低频区域,SONAH算法和ESM算法保留了更多的声压信息,对声场信号有较好的还原效果,重建精度优于STSF算法。ESM算法对声场信息还原最好,但容易产生虚像,造成噪声源定位偏差。STSF算法具有较好的声源定位效果,但忽略了其他微弱的声场信息,重建误差较大,且受声源频率变化的影响较为明显。当声源频率增大时算法的重建精度逐渐降低,且ESM>SONAH>STSF。
5.2.2 根据距离变化的重建精度比较
将距离换能器0.05 m处声场面作为重建面,发出频率为1 kHz的声波,分别测量距离为0.15 m、0.25 m、0.35 m处的声场分布作为测量面。计算不同算法对应各个重建距离的重建误差,重建效果与重建误差如图8与表2所示。

图8 3种算法在不同重建距离下的重建效果Fig.8 Reconstruction effects of three algorithms at different reconstruction distances

表2 不同重建距离下的重建误差Tab.2 The reconstruction error of each distances dB
通过对比可以看出随着重建距离增大,重建误差都逐渐变大。SONAH与ESM具有较强的重建效果, STSF算法除了有较好的定位能力, 对声压信息还原较差,受重建距离变化的影响最大。ESM与STSF由于算法中格林函数受距离变化影响较大,从而在重建计算中产生虚像和旁瓣,因此误差增加明显,其中STSF算法尤为明显。
5.2.3 根据采样点数变化的精度比较
对水听器阵列进行调整,分析对比水听器采样点数为7×8个、7×12个、7×24个情况下的声场重建效果。重建效果与重建误差如图9与表3所示。

图9 3种算法在不同采样点数下的重建效果Fig.9 The reconstruction effect of three algorithms at different number of sampling points

表3 不同采样点数时的重建误差Tab.3 The reconstruction error of each sampling points number dB
经过比较可以看出随着测量点数的减少, 声场信息也在减少,各算法的重建效果区别变得不明显。当测量点数增多时,SONAH算法有比较理想的精度,随着测量点数减少,ESM算法表现出较大的优势。
测量点数的变化造成声场数据量增多,使矩阵运算维度增大引起计算效率差异,为对比采样率对算法的影响,对3种算法的计算效率进行比较,不同采样率下算法的运算时间如表4所示。由表4可以看出STSF算法始终保持着高速的计算效率,而 SONAH算法由于涉及矩阵运算,当采样率变大时声场重建运算效率降低,在3种算法中计算速度最慢。ESM算法速度较为稳定,受采样率的影响较小。

表4 不同采样点数时的计算时间Tab.4 Operation time at different number of sampling points s
5.2.4 正则化参数比较
正则化的主要作用是减少噪声信号对信号源分析的影响,对测量面的声场信息人为加入方差为36,均值为0的高斯噪声,再用混入噪声的测量面声信号进行声场重建。
本次实验所用声源频率为1 000 Hz,测量面距声源0.15 m,重建面距声源0.05 m,采样点数选取 7×24个,选取不同正则化参数进行声场重建,效果对比如图10所示。
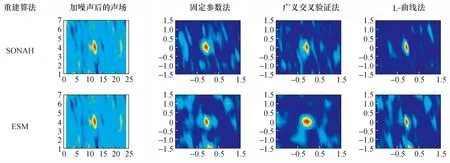
图10 3种正则化参数选取方法对重建效果的影响Fig.10 The reconstruction effect of three regularization parameter selection methods
可以看出,在3种正则化方法中广义交叉验证法的降噪效果最好,L-曲线法对噪声源的还原能力最强。SONAH算法与L-曲线法结合的近场声全息既能有效保留声场信息,又能对噪声进行抑制,在该工况下具有最好的重建效果。
6 结 论
通过声源频率、重建距离、传感器阵列的采样点数及正则化参数的选取这4种对声场重建影响较大的因素分析3种常用的近场声全息算法在不同工况下的优劣,分别对各自算法进行了仿真趋势分析和实验重建效果验证,得到以下结论:
1) 随着声源频率降低,重建距离减小,采样率增加,算法的重建精度提高;
2) STSF算法速度最快,对声源有较好的定位效果,然而声场重建精度受重建距离影响明显,微弱信号声场信息丢失严重,因此该算法适用于对噪声定位具有高速且准确定位的应用场合,如海洋军事与航天航空领域雷达定位、水域环境探测等;
3) SONAH算法重建效果良好,且能保留较多声场信息,配合L-曲线正则化法后对噪声能进行有效抑制,但受测量点数影响较大,计算速度缓慢,适用于对计算速度要求较低且需要声场有效还原的应用领域,如房间声场噪声分析等;
4) ESM算法有较好的重建精度和速度,结合正则化法后对声场信息保留情况较好,但在计算过程中对声源位置有预测要求,因此适用于近距离下,声源位置误差较小的非接触式噪声分析,如机械结构噪音定位等。
