拉曼光谱仪成像定位精度检测方法

定 翔， 付彦哲， 李 飞， 刘文丽

(中国计量科学研究院，北京100029)

1 引 言

将拉曼光谱技术与显微成像技术结合，能够同时获取样品的拉曼光谱和不同组分的空间分布信息，已被广泛应用于化学、地理、生物、安检等领域[1～5]。近年来，国内外涌现出众多拉曼光谱仪品牌，不同品牌厂商的仪器性能评价方法不同，缺少统一评价标准。激光共焦拉曼光谱仪的性能参数主要包括光谱类参数和成像类参数。目前，光谱类参数的校准方法和量值溯源体系已经建立，但是成像类参数的校准问题尚未见相关解决方法的报道[6]。

1990年Pupples G J等[7]提出的激光共焦拉曼光谱系统已成为现阶段商品化仪器最为常见的形式[8,9]。文献[10～12]针对这类仪器的成像性能进行分析，大部分是基于单一理论分析得到结果。而仪器真实的性能除了受折射和衍射理论决定外，还同样受到探测器像元尺寸、灵敏度、三维移动平台精度和样品本身的影响[13]。激光共焦拉曼光谱仪通常采用逐点扫描的方式进行成像。如果三维移动平台定位不准确，图像就会产生畸变，与真实的样品结构和尺寸不匹配，从而引入测量误差。真实物体具有明确的边界，其空间位置可以直接通过测量得到。但拉曼图像在成像过程中受到系统点扩散函数的影响，其边界是一个模糊的过渡，难以确定其准确位置。

本文提出了一种拉曼成像定位精度检测方法，进一步提出通过对边缘扩展函数微分来寻找边界点的方法，获得比较图像上与样品对应位置点的坐标和计算相应点间的距离，可以测量得到拉曼图像的定位精度。该方法基于实验测量方法来检测激光共焦拉曼光谱仪图像位置精度，对于评估拉曼光谱仪成像性能的客观评价具有一定的意义。

2 理论与方法

激光共焦拉曼光谱仪成像满足线性和空间不变性，其成像过程可以视为物函数与系统点扩散函数卷积的结果[14]，如图1所示。

图1 激光共焦拉曼光谱仪成像原理Fig.1 The imaging process of the confocal Raman microscope

由于点扩散函数的作用，原本清晰的样品轮廓经过成像后变得模糊。模糊的边缘无法直接用于评估成像定位的准确性。这种现象是由于随着激光光斑激发区域的增加，靶标边缘处的拉曼光谱强度信号会随之增加。其对应的信号响应曲线是阶跃函数响应曲线，也被称为边缘扩散函数(edge spread function，ESF)。将边缘扩散函数微分可以得到系统的线扩散函数(line spread function，LSF)。线扩散函数反映了系统在该方向上的成像性能，其最大值对应点的坐标代表了激光光斑中心照射在样品边缘处时的位置。通过对已知间隔的2个ESF进行微分，就可以得到图像上对应位置之间的间隔距离，以此评价图像与样品的尺寸误差。

利用金属对激光的阻挡作用和无拉曼信号的特点，可以设计出图2所示的样品结构。在硅片表面镀上一层几十 nm厚的金属薄膜图样，可以利用图样的边缘对拉曼光谱仪的成像定位精度进行检测。

图2 定位精度测量模体Fig.2 The phantom for measuring the positioning accuracy

可以通过数值模拟分析该样品的成像过程。设定每个靶标图形的宽度为10 μm，按图2所示箭头指示方向提取样品成像后的拉曼信号强度曲线，见图3。 水平截面强度分布结果如图3(a)所示； 将信号强度曲线微分可得到如图3(b)所示的结果。每个尖峰对应了激光光斑中心刚好照射到样品金属图形边界处的位置。计算对应两个尖峰之间的距离，可以得到拉曼图像中两个图形间的距离。通过比较尖峰之间的间距和样品实际的图形宽度，可计算出定位误差。通过数值模拟，计算得到边缘扩展函数尖峰的间距为10 μm，这说明该方法引入理论误差较小，可以用于检测拉曼光谱仪的成像定位精度。

图3 拉曼信号强度曲线Fig.3 The intensity curve of Raman signal

3 实验参数与结果

3.1 实验参数

实验采用Renishaw Invia型激光共焦拉曼光谱仪，激光波长为532 nm，物镜放大倍数为100，数值孔径为0.85，光栅密度为24 001/mm，狭缝宽度为65 μm，室温为(20±1) ℃。通过在硅表面镀一层70 nm厚的铬制作实验样品形成硅-铬模体，其显微图如图4所示。长方形区域为铬，背景区域为硅。金属没有拉曼散射信号，且能有效地阻挡激光。激光在扫描过程中，随着激光光斑从硅表面移动到铬表面，硅的受激发区域逐渐减小，拉曼信号强度也随之逐渐减小，信号呈现出典型的阶跃函数响应曲线的特点[15]。每个铬图形宽度和间距均为30 μm，扫描成像的步距为0.2 μm。

图4 硅-铬模体显微图Fig.4 The microscopic image of the Si-Cr phantom

3.2 实验结果

以扫描移动的距离为横坐标，硅在520 cm-1附近拉曼峰的信号强度为纵坐标并进行归一化，可得到强度-位移曲线，如图5所示。

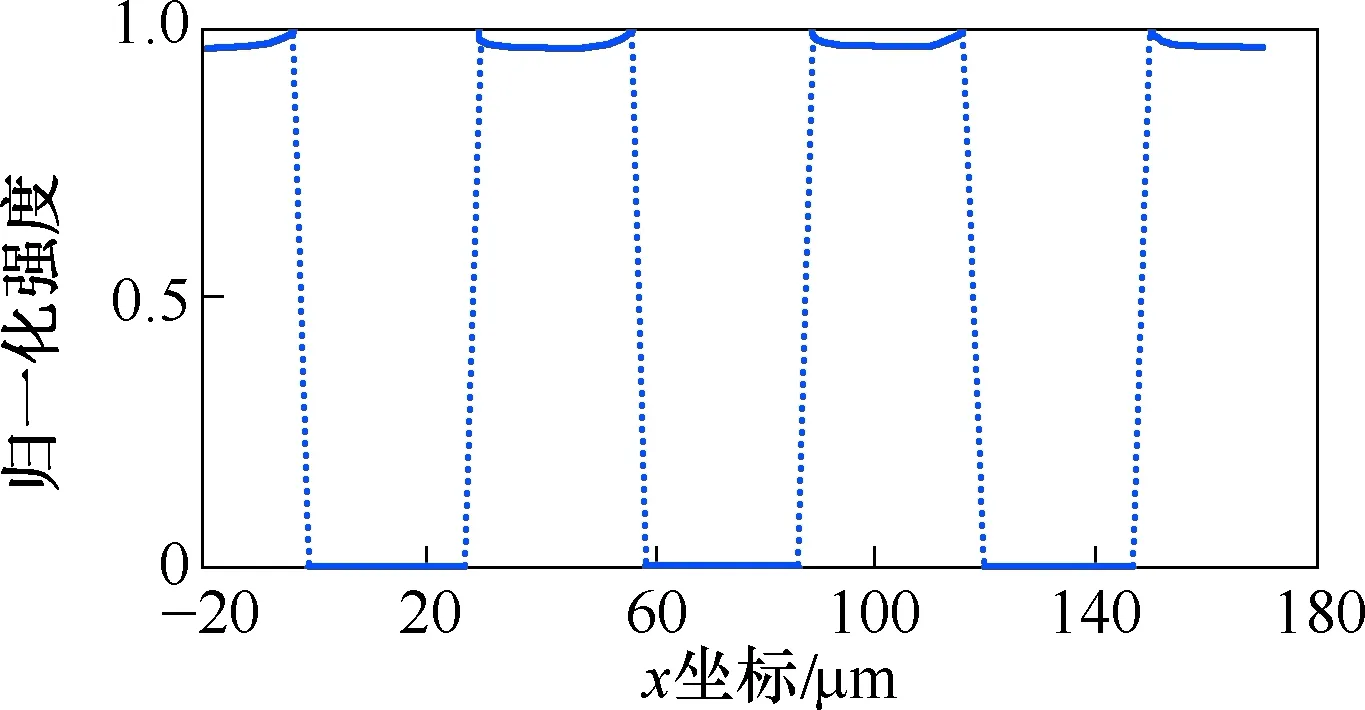
图5 横向扫描结果Fig.5 The result in x direction

激光共焦拉曼光谱仪采用的是点扫描模式，离散的点在微分后，噪声会被显著放大，导致边缘扩展函数的峰值位置不准。通过采用Fermi函数对阶跃响应函数进行拟合来提高测量精度[16]。Fermi函数的模型为：

(1)

式中：x为水平方向坐标；a,b,c为Fermi函数参数。

分别截取两段数据，采用Fermi函数拟合，结果如图6所示。图6中R-square代表模型对数据的拟合程度。2次测量结果的R-square值分别为0.999 8和0.999 7，这表明Fermi函数能够对测量数据进行很好地拟合。将2组拟合结果分别微分得到实验结果如图7所示。2组数据的极小值点坐标分别为0.4 μm和61.0 μm，两点间距离为60.6 μm，靶标尺寸的设计值。采用该方法重复测量6次，得到实验结果见表1。

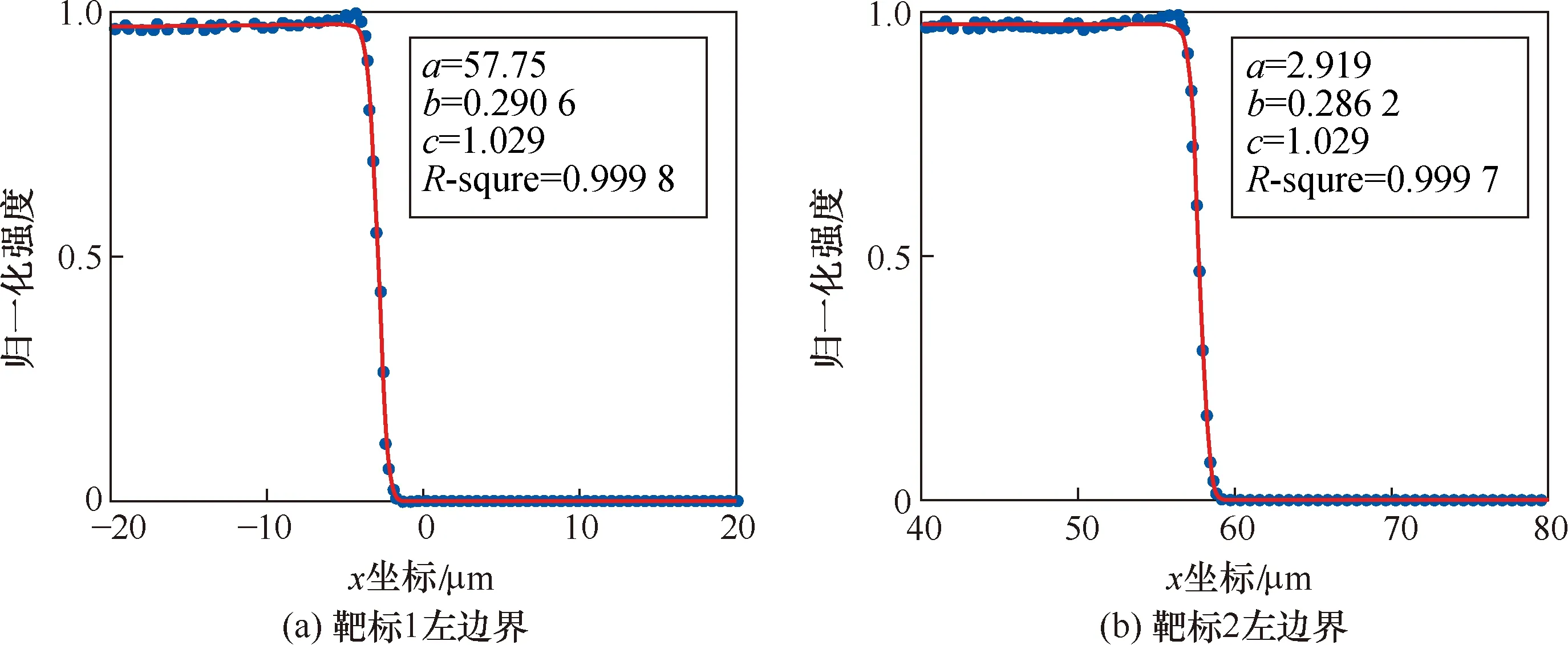
图6 Fermi函数拟合结果Fig.6 The result of Fermi function fitting

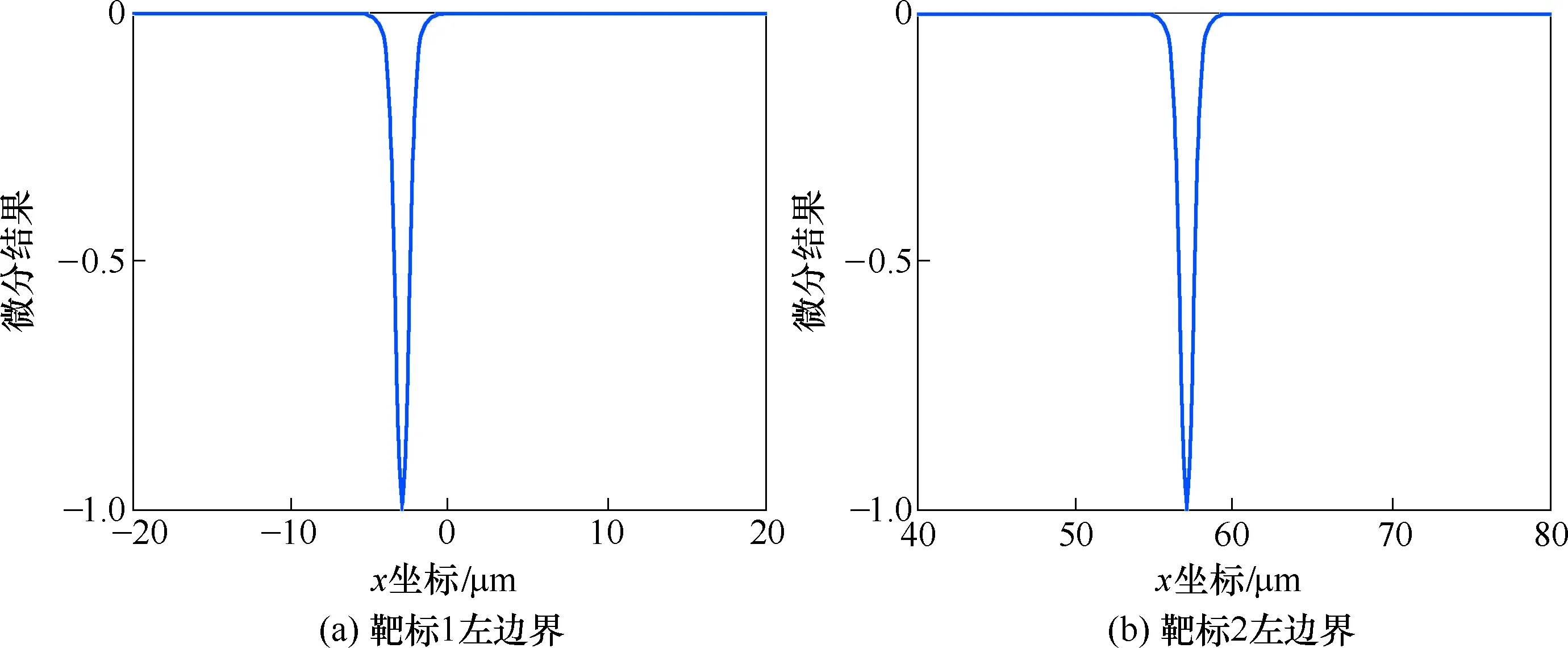
图7 Fermi函数拟合微分后的结果Fig.7 The differential result of Fermi function fitting

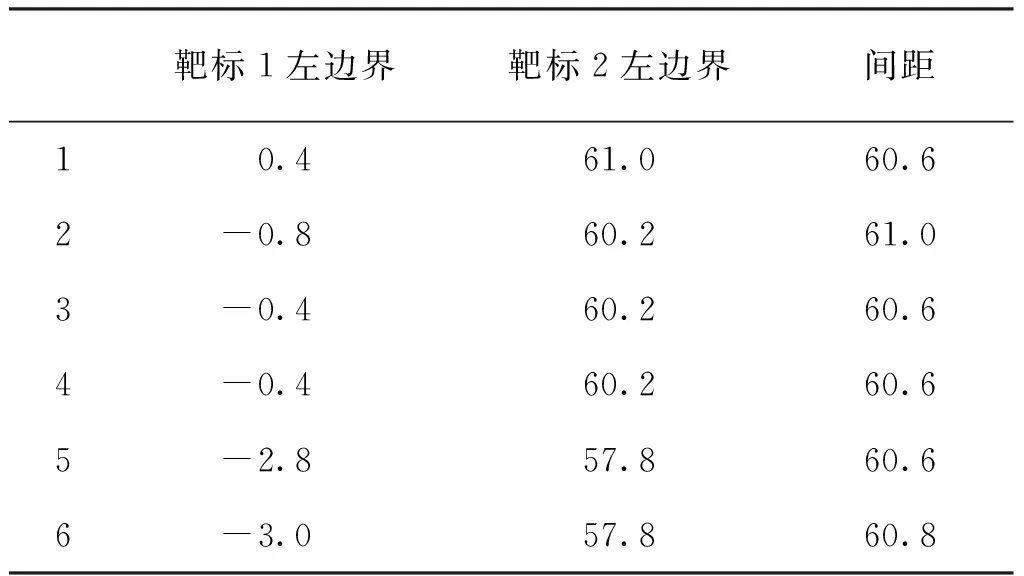
表1 图像位置精度Tab.1 Positioning accuracy μm

6次测量结果的平均值约为60.7 μm，重复性约为0.2 μm。

5 结 论

本文针对因采用点扫描方式成像导致的图像位置和样品实际位置不匹配的问题，提出了可用于拉曼成像定位精度的客观测量方法，并提出了求取线扩散函数来寻找边界来提高测量精度的方法。建立了基于线扩散函数的测量模型，通过数值模拟证明了该方法的理论可行性。设计和制作了基于硅基底的金属图形样品，对商业化激光共焦拉曼光谱仪进行实验测试，仪器的定位重复性为0.2 μm，验证了该方法的可行性，实验结果具有良好的稳定性。