超声测流装置的实验室测试与优化

刘敦利, 蔡 勤, 胡鹤鸣

(1. 新疆维吾尔自治区计量测试研究院,新疆 乌鲁木齐 830011; 2. 中国计量科学研究院, 北京 100029)

1 引 言

大口径管道流量的在线校准主要有3种方法:插入式的点流速面积法、外夹式或插入式的线流速面积法和全截面多点流速法。其中最常用的方法是基于外夹式超声流量计的线流速面积法。朱永宏等[1]提出利用外夹式超声波流量计对大口径电磁流量计进行在线核查,起到延长检定周期的作用。苗豫生等[2]采用多台外夹式超声流量计对同一台大口径流量计进行测试,验证应用外夹式超声流量计进行大口径流量计在线校准的可行性与可靠性。然而,外夹式超声流量计一般为单声道或者双声道,受管道、介质、安装等各方面条件的限制,其本身的测量误差都在2%～5%,无法实现对管道上标称准确度为0.5%～1%的流量计进行有效的校准。为此,许多学者从硬件和软件方面都做了相关研究。袁易全[3]提出一种高灵敏管外夹式超声流量计传感器,经过系数修正后可准确度达到1%。王艳霞等[4]基于混合长度理论对流场的流速分布进行补偿并建立数学模型,提出了一种高精度在线检测方法和装置。Kang L等[5]应用空间平均算法提出了一种新型二维弯曲超声阵列换能器,提高了单声道超声流量计的测量精度和降低了测量不确定度。

本文从超声流量计的计量原理出发,改外夹式为插入式,增加声道数量[6],精确测量管道和探头的几何参数[7],并进行数据处理和优化[8],形成了一套完整的超声测流装置,用于对大口径管道流量计的现场校准。装置的技术核心在于精确的超声传播时间测量、准确的探头定位和几何参数测量、适应现场条件的流速代表性算法。本文利用实流实验来探讨其应用于大口径管道流量在线校准的可行性与可靠性。

2 测流管段设计

实验选用管道的内直径400 mm,长度1 000 mm,不锈钢材质。通过对几何参数的计算,在管道上确定探头的安装位置,打孔、焊接套管、安装探头、接入主机,完成对超声测流装置的安装。同时采用关节臂式坐标测量机对探头的声道角、声道高度、声道距离等参数进行实测,对各声道流速的权重系数进行修正,把修正后的参数代入流量计算模型,实现流量测量。同时,改变探头在管道内部全突、中间、全缩3种安装状态,分析装置测量误差的变化情况,并对误差进行修正,找出超声测流装置的最优化安装方案[9,10]。

2.1 声道配置方案

实验选用交叉4声道设计,探头位置见图1所示,几何参数设计值见表1所示。图1中,AU1～AU4、AD1～AD4、BU1～BU4、BD1～BD4为探头;A1～A4、B1～B4为声道;α1～α4为声道高度角;φA、φB为2个声道面的声道角,d1～d4为声道高度,R为管道半径。

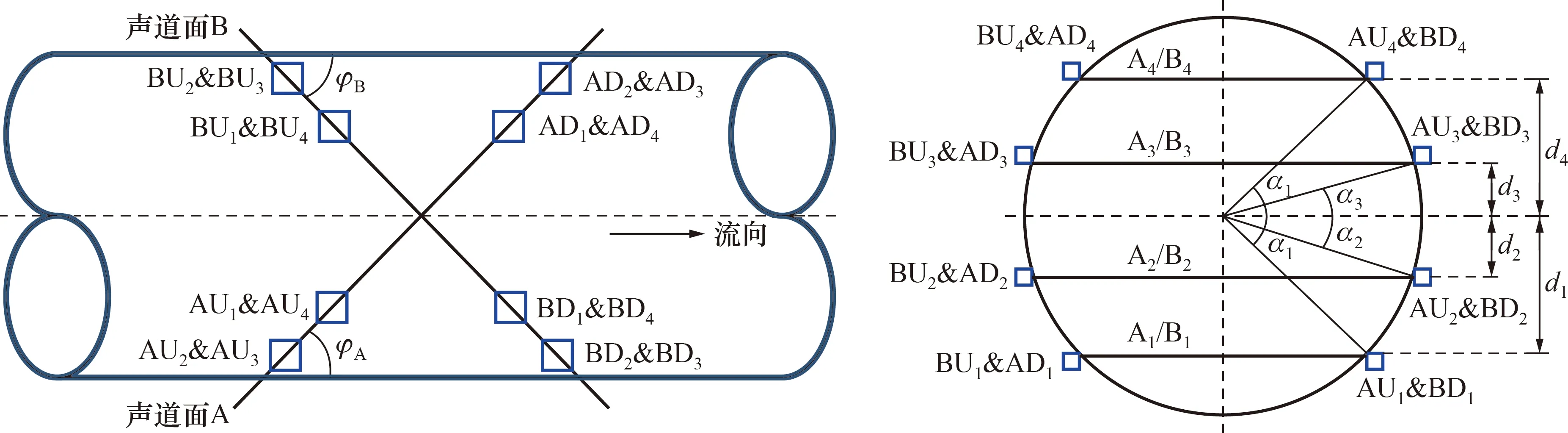
图1 超声探头位置Fig.1 Position of ultrasonic probe

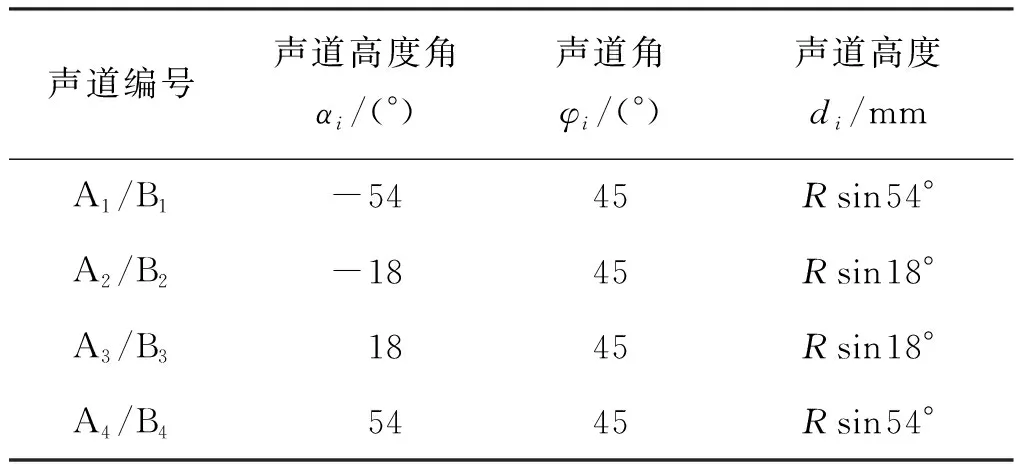
表1 几何参数Tab.1 Geometric parameters

2.2 探头定位及开孔方法

探头采用斜插式,声道角为45°,根据表1中的设计参数确定并标记各探头的安装位置。如图2所示,顺着流向,左侧探头自下而上依次为AU1～AU4,右侧探头依次为BU1～BU4;面向流向,左侧探头自下而上依次为AD1～AD4,右侧探头依次为 BD1～BD4。

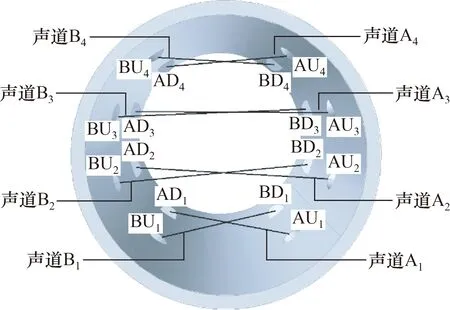
图2 探头安装示意图(顺流向)Fig.2 View of probe installation (follow the flow direction)

为了模拟大口径管道现场校准的过程,探头定位及开孔并未在数控机床上进行,而是专门设计了一套现场定位和开孔方法。首先利用关节臂式坐标测量机测量管道外圆柱并拟合外直径[11],然后利用超声测厚仪测量管段的厚度;在管道内外直径基础上,结合表1中的设计参数,可以将每一个开孔位置绘制在柱面展开图上;根据展开图中的定位坐标,在探头安装位置旁合适位置焊接开孔导向支架,保证探头的水平和声道角,利用开孔取芯钻来进行管段的斜孔开孔,如图3所示,其中左下角的圆柱为管段开孔时取出的钻芯;完成开孔后,将探头底座焊接在开孔位置,实验时可将探头插入并用螺纹紧固即可。

图3 管道打孔Fig.3 Pipeline drilling

2.3 几何参数的测量

利用关节臂测量管道外部特征,可以计算超声测流装置相关的几何参数。测量过程分为2个步骤:1)使用关节臂式坐标测量机对足够多的管道外壁点进行三坐标测量,可以拟合得到被测管道的外半径和虚拟中心轴线。2)对探头底座圆柱特征进行三坐标测量,并结合探头插入深度可以拟合得到探头内圆心三坐标,进而得到声道长度、声道角、声道高度,其中声道角是声道虚拟线与管道虚拟轴线的夹角,声道高度是声道虚拟线与管道虚拟轴线的空间距离。

基于实验的需要,探头在全缩、中间、全突3种状态下,关节臂式坐标测量机测得各声道的声道角和声道长度见表2。考虑到实验室测试管道内部的可测量性,还采用管道内部特征测量方法利用关节臂直接对超声测流装置几何参数进行了复测,两者数据差异导致的流量偏差小于0.2%,确认了外部特征测量法的可靠性。

表2 3种状态下各声道的声道角和声道长度Tab.3 The each channel angle and length under three conditions

把全缩、中间、全突3种状态下实测的声道几何参数输入测流装置主机软件,基于超声时间差测量和几何参数测量的高准确性,超声测流装置测得的各声道流速数据不依赖于其它标定系数,是一种绝对流速测量方法,可视为真实可靠的数据[12～14]。

3 流量计算模型

3.1 声道层流速的计算

根据超声时差法的测量原理[15],声道在管道轴向上的流速为:

(1)

式中:vax为轴向流速;L为声道长度;φ为声道角;tu、td分别为逆流和顺流传播时间。

鉴于测流装置所处流道可能具有横向流动,采用交叉声道面配置可有效削弱横向流动的干扰。声道投影流速与垂直于声道层的流速分量无关,假设声道层内两声道上的线平均流速vlayer,A和vlayer,B分量相等,即:

vlayer=vlayer,A=vlayer,B

(2)

式中:vlayer为流速,可分解为轴向流速vax和横向流速vtr,其中vax是测流装置希望测到的轴向流速,如图4所示。当存在横向流速vtr时,测到的声道投影流速分别为:

(3)

式中:vproj,A、vproj,B分别为声道层内2个声道上的投影流速;φA、φB分别为2个声道的声道角;θ为流速vlayer与流道轴向的夹角。

换算到声道轴向流速:

(4)

利用几何计算可得到,待测的声道轴向流速:

(5)

当声道角φA=φB时,可以简化为:

vax=(vA+vB)/2

(6)

管道内的实际流动vlayer存在横向流动vtr时,声道投影流速vproj,A/B、声道轴向流速vA/B和待测流速vax之间的关系如图4所示。所以,如果采用单声道面配置,将存在较大的流速测量误差,利用交叉声道面可以有效提高测流装置的准确度。

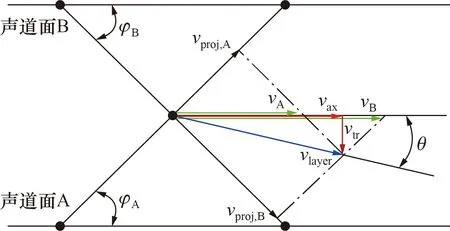
图4 存在横向流动时声道轴向流速示意图Fig.4 Axial velocity of sound channel with transverse flow

3.2 流量的计算

管道中,不同声道层的声道轴向流速代表了其上下一定区域内的平均流速,利用多个声道轴向流速计算出管道的平均流速,与流道断面面积的乘积,得到流量:

Q=Avax=Af(vax,1,vax,2,…,vax,n)

(7)

式中:A为流道断面面积,n为声道数。

由于边缘效应的存在,管道内的流场分布是不均匀的,通过采用加权平均的方法计算流量[16,17]。不同声路的权重系数和声道高度通常采用高斯-雅克比积分法(Gauss-Jacobi)和圆形优化积分法(OWICS)确定,后者考虑了边壁附近的零流速,系统偏差略小,具有一定优势,因此本实验采用圆形优化法[18,19]。相同声道高度布置下,2种方法的权重系数wi见表3。流量加权计算公式为:

表3 相同声道高度条件下的权重系数(4声道)Tab.3 Weight coefficient at the same channel height (4 channels)

(8)

若令Wi=wicosαi,公式简化为:

(9)

式中:R为管道内半径;wi为i声道的权重系数;vax,i为各声道平均轴向流速;Lw,i为声道i声道长度。

3.3 基于实测声道高度的修正

换能器安装后复测时,声道高度通常会与设计值存在一定差异,宜根据实测的相对声道高度ti=hi/R来修正相应的权重系数,hi为声道i声道高度。对于4声道配置的超声测流装置,权重系数修正公式为:

(10)

式中:对于高斯-雅克比积分法,参数κ=0.5，g1(κ)=1.570 796,g2(κ)=0.392 699;对于最佳圆断面积分法,参数κ=0.6，g1(κ)=1.513 365,g2(κ)=0.360 325。本实验基于实测声道高度和高度角对权重系数进行修正,得到结果见表4所示。

表4 各声道的声道高度及权重修正系数Tab.4 Channel height and weight correction coefficient of each channel

4 实流测试

4.1 测试方案

实验在静态质量法水流量标准装置上进行。装置扩展不确定度U=0.05%,k=2,满足0.2级及以下流量计的溯源要求。把超声测流装置安装在标准装置上,在探头的3种状态下,分别选择50,100,200,400,800,1 600 m3/h等6个流量点,每个点测量3次。测流装置的软件采集时间、瞬时流量、累积流量、各声道流速、声道截面流量、各声道顺流和逆流时间等参数,采集间隔1 s,取算数平均值。

4.2 流量示值误差分析

本次实验以超声测流装置测得的流速数据为基础,基于权重修正系数按照式(5)计算瞬时流量,同时以静态质量法标准装置的值为标准值,计算流量示值误差[15],见图5。由图5可以得出:

图5 3种状态下流量示值误差Fig.5 Flow indication errors under three conditions

1) 3种状态下,流量示值误差均为负值,且有明显的差异;其中全突状态误差最小,全缩状态误差最大,中间状态居中。

2) 全突和中间状态下,流量示值误差呈非线性变化,随着流量的增大示值误差绝对值逐渐增大;全缩状态下,流量示值误差基本呈线性变化,随着流量的增大示值误差变化较小,一致性较好。

对3种状态下流量示值误差进行修正,修正系数K为:

(11)

式中:xi为示值误差;(xi)max、(xi)min分别为示值误差的最大值和最小值。

示值误差修正公式为:

(12)

图6 修正后3种状态下流量示值误差Fig.6 Flow indication error under three modified conditions

由图6可以看出,经过系数修正后,3种状态下流量示值误差均能够满足1.0级要求,其中中间状态满足0.5级要求,全缩状态下满足0.2级要求。即经过有效的系数修正后,超声测流装置在全缩状态下的计量准确性最高,最高可达到0.2级。

5 结 论

1) 为解决大口径管道流量在线校准问题,建立一套多声道超声测流装置,并对其现场探头定位安装及几何测量方法进行了优化,实验室测试数据具有良好的线性和重复性,证明其可用于在线校准的可行性。

2) 探头不同插入深度直接影响超声测流装置对圆形管道流量的测量结果,随着插入深度的增加,流量测量结果逐渐增大,但即使全突状态流量依然偏小。3种状态中全缩线性较好。经过系数修正后,超声测流装置在探头全缩安装状态下的计量准确性最高。

3) 实验已发现不同管径的修正系数具有差异性,修正系数呈现出随管径增大而减小的趋势,后续将对更多的管径进行测试,建立管径与修正系数的关系模型。