活塞式气体流量标准装置活塞缸内径测量及不确定度评估

李培晶, 崔骊水, 李春辉

(中国计量科学研究院,北京100029)

1 引 言

随着生物医药、半导体工业、国际贸易[1]、环境监测[2]等领域的发展,微小气体流量准确计量的需求日益凸显[3]。活塞式气体流量标准装置具有结构简单、对环境要求低等优点[4,5],在气体小流量测量中具有明显优势。德国物理技术研究院(PTB)[6]、美国国家标准技术研究所(NIST)[7]、韩国标准科学研究院(KRISS)[8]、意大利国家计量院(INRIM)[9]等国家计量院均已建立活塞式气体流量装置用以实现其最小气体流量的计量。

活塞式气体流量标准装置可分为被动式活塞及主动式活塞2种[10],被动式和主动式活塞的最大不同在于前者没有外部驱动设备,活塞依靠缸内压力与大气压力形成的压力差进行运动,结构相对简单。为提高我国气体流量标准装置的技术能力,满足高准确度气体小流量溯源的需求,中国计量科学研究院(NIM)将建立被动式活塞气体流量标准装置(以下简称活塞装置)。

在已有对活塞缸的内径测量研究中,对活塞缸的几何形状特征研究较少,对活塞缸整体均匀性的分析不够,未就活塞缸内表面的形状分布对活塞装置流量测量的影响进行定量分析,导致测量不确定度分析不全面。此外,内径表和标准环规在使用过程均由人工手动进行,容易对活塞缸内表面造成划损[15]。本文使用三坐标测量机对活塞缸内外表面坐标点自动采集,系统分析活塞缸整体的一致性影响,验证三坐标测量机测量的可靠性的同时,完善形状特征测量不确定度影响分析,并对其测量不确定度进行了完整评估。

2 基本原理

活塞装置工作过程中,通过调节上游流量调节阀产生持续平稳的气体流量,气体进入活塞缸内推动活塞向上做匀速运动,测量原理[11]如式(1)所示。

(1)

式中:Qv为标准装置测量得到的体积流量,由气体流经标准装置的体积V和时间t确定；D为活塞缸的内径；l为活塞运动有效长度。

基于式(1),活塞装置的不确定度ur(Qv),如式(2)所示。

(2)

式中:ur(D)为活塞缸内径测量带来的不确定度；ur(l)为活塞运动长度测量带来的不确定度；ur(t)为活塞运动时间测量带来的不确定度。

内径测量带来的不确定度在3个影响量中灵敏度系数最大,为影响活塞装置不确定度的首要因素[12,13]。

由于活塞缸的内径较小,且待测量长度较长,测量器具的选择受到空间的制约[14]。NIST采用内径表对活塞缸不同位置的内径进行测量,其中内径表在使用前通过标准环规校准[7]。KRISS采用标准环规对活塞缸的上部、中部、下部的内径进行直接读取,将3部分的内径取平均值作为活塞缸的内径[8],研究表明:环境温度在(20～28)℃范围内,活塞缸内径的变化小于0.3 μm,可忽略活塞缸热膨胀影响。

3 活塞缸测量方案

活塞缸是活塞装置的主体,为保证活塞装置的密封和使用稳定,活塞缸体的加工要求较高。石英玻璃管在同轴度、抗压性、防泄漏等方面具有很好的性能,所以活塞缸选择如图1所示,长度1 000 mm,名义内径分别为19 mm、45 mm和140 mm的石英玻璃管(以下简称玻璃管)。

图1 玻璃管Fig.1 The glass tube

玻璃管的几何参数使用NIM的Leitz PMM-C三坐标测量机,在(20±0.2)℃下进行测量,如图2(a)所示。测量用三坐标测量机主要由控制系统、封闭框架和测针3部分组成。1)控制系统:控制测针自动进行测量并完成数据处理及分析,减少人为因素干扰。2)封闭框架:由固定桥架和活动工作台组成,是整个测量机的主体部分,保证测量系统的刚性和稳定性。3)测针:三坐标测量机的核心部分,如图2(b)所示,测针由测头和测头杆2部分组成。测头选用球径为8 mm的红宝石球,每次测量前使用标准球对测头直径进行校准。测头杆材质为陶瓷,其特点是质量轻、硬度高,可有效减少测量中扰动对测量结果的影响。

图2 三坐标机测量机Fig.2 The three coordinate measuring machine

由于玻璃管易碎,测量过程中,将玻璃管水平放在三坐标测量机的工作平台上,两端用特制的夹具固定,以玻璃管端面圆心为坐标原点,建立xyz三维坐标系。三坐标测量机对玻璃管直径的测量基于圆的最小二乘法拟合,将整个玻璃管沿轴向方向划分为不同的测量圆周,通过采集不同测量圆周的坐标点拟合得到多组直径值,玻璃管的直径值为多组测量圆周的直径值的平均值。

以名义内径为140 mm玻璃管的一个测量圆周为例,已知一个测量圆周的坐标点集(xm,ym),m=1,2,…,30。假设理想圆的方程为(x-A)2+(y-B)2=R2,其中(A,B)为理想圆的圆心,R为理想圆的半径。则坐标点到理想圆圆心距离的平方与半径平方的差如式(3)所示。

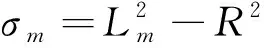
(3)

式中:a=-2A,b=-2B,c=A2+B2-R2。

最小二乘法原理如式(4)所示,当式(4)达到最小时,得到理想圆的方程,理想圆的直径即为测量圆周的直径。通过Matlab软件拟合,理想圆和坐标点集的结果如图3所示。

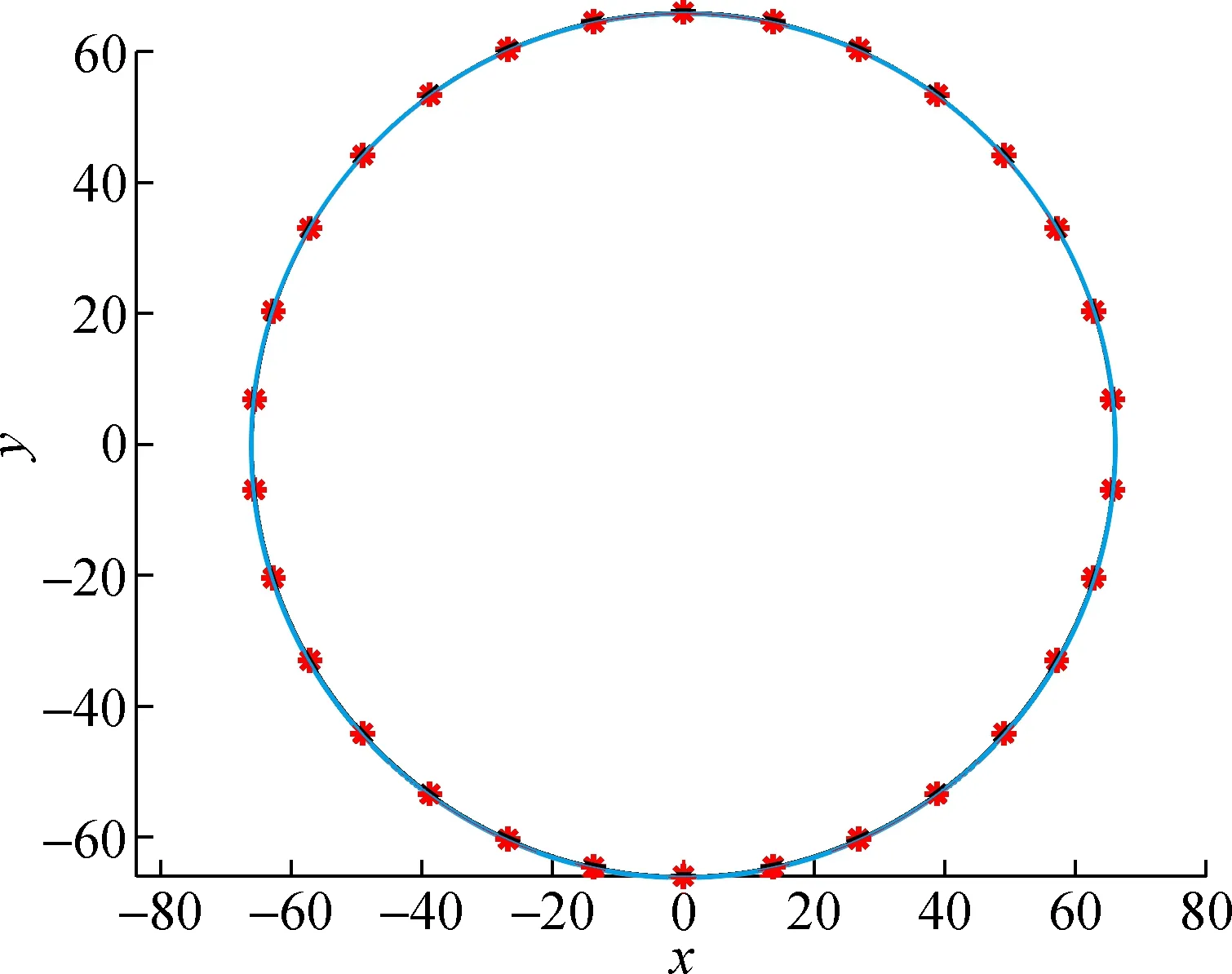
图3 Matlab软件拟合结果Fig.3 The fitted results of Matlab

(4)

玻璃管的有效使用位置为距离两边端面 200 mm 的中间部分,使用三坐标测量机对玻璃管的内径进行测量时,受测针有效测量长度的限制,测头对玻璃管内壁的探测距离有限,只能分别测量距离端面100 mm以内的内径,不能测量整根玻璃管的内径。玻璃管采用预制棒热加工工艺,在高温和管内负压的作用下,玻璃管内壁会紧贴在圆柱形的预制棒上。为使冷却状态下玻璃管更好地从预制棒上取出,预制棒的端面设置有锥形的缩口[16],因此,玻璃管中间部分的均匀性显著优于两端的均匀性。基于此,本文通过分析玻璃管两端的均匀性验证玻璃管中间部分的均匀性,并以两端的内径作为玻璃管整体的内径。

内径测量: 分别以两端端面内圆为起始测量圆周,定义为OIA,1、OIB,1,测针的轴线方向与玻璃管轴线平行,沿x轴每隔3 mm取测量圆周,在每个测量圆周沿360°每间隔12°取坐标点,得到每个测量圆周的内径d1,两端各得34个测量圆周,令两端测量圆周的内径分别为:kIA,i、dIB,j(i,j=1,2,…,34),如图4(a)所示。已知每个测量圆周的直径值,玻璃管两端的内径平均值如式(5)[12]计算。

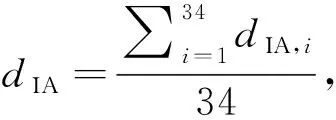
(5)

玻璃管的内径D和标准差分σ(D)分别由式(6)、式(7)计算。

(6)

(7)

外径测量: 以端面外圆为起始测量圆周,测针的轴线方向与玻璃管轴线垂直,沿x轴每隔15 mm取测量圆周,在每个测量圆周的上圆周180°内每间隔12°取坐标点,得到每个测量圆周的外径do,k(k=1,2,…,65),如图4(b)所示。

图4 玻璃管内径、外径测量Fig.4 The measurement for the inner and external diameter of glass tube

厚度测量: 三坐标测量机对玻璃管厚度的测量,通过外径、内径测量值的差值计算得到。考虑测量结果的独立性,仅取位于偶数位置的测量圆周参与计算,如式(8)所示。

(8)

4 测量结果及不确定度分析

玻璃管两端的内径测量结果如图5所示,在有效使用范围内玻璃管的内径重复性优于两端的内径重复性,在0.013%以内。玻璃管两端内径的差异带来的相对误差为0.028%,以两端内径的平均值作为玻璃管的内径,即通过式(6)计算玻璃管内径的前提是玻璃管整体良好的均匀性,因此,在测量结果中需要分析玻璃管均匀性对测量结果的影响。

图5 两端内径与平均内径值的偏差Fig.5 The deviation of the inner diameter between the value at both ends and the average value

如图6(a)所示,在一个测量圆周上,三坐标测量机采集到的坐标点并不能完全落在理想圆上,坐标点在理想圆周围的偏离情况表现为玻璃管内部真实的形状分布[17]。

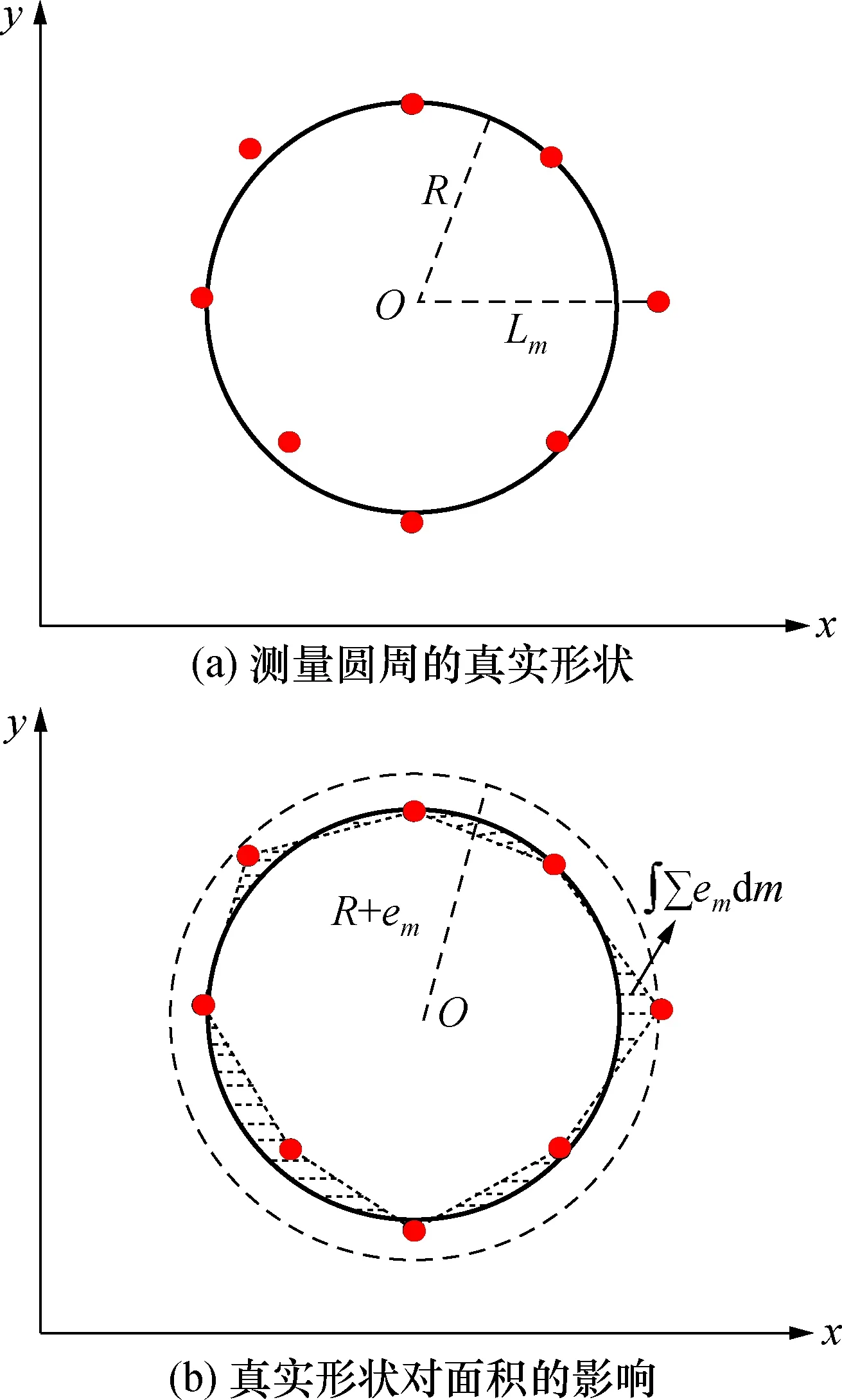
图6 圆心偏离度的影响Fig.6 The roundness effect

根据式(1),标准装置测量过程中将玻璃管当作理想圆柱体,计算气体流过的体积量表示为:

V=Scir·l= πR2·l

(9)

如果加工水平粗糙,玻璃管内部的真实形状将远远偏离标准圆,如图6(a)所示,导致圆面积Scir≠ πR2,此时体积量的计算将与真实情况不符,因此,玻璃管的圆度是内径测量不确定度的来源之一。

玻璃管的同心度通过外径测量圆周的同心度予以评估,通过最小二乘法拟合得到测量圆周的圆心空间直线。在有效使用距离内,如图7所示,圆心到空间直线的最大偏离量s为0.09 mm,最大偏离角γ为0.5°(tanγ=1.5×10-4),对长度的影响量为 10-6mm,可忽略不计。

图7 测量圆周的圆心到拟合直线的偏离量Fig.7 The deviation from the center of the circle to the fitted line

因此,影响内径测量的主要因素有:三坐标测量机；玻璃管均匀性；玻璃管圆度；测量重复性。此外,玻璃管的线膨胀系数以及表面粗糙度带来的影响很小,可忽略不计[8],环境对三坐标测量机的影响以及最小二乘法拟合的影响已包括在三坐标测量机的测量不确定中。

4.1 三坐标测量机引入的测量不确定度u1

三坐标测量机测量的最大允许误差为±(0.5 μm+H/1 000),矩形分布,其中H为玻璃管的名义内径,mm。三坐标测量机引入的测量不确定度如表1所示。

表1 三坐标测量机的测量不确定度u1Tab.1 The uncertainty resulted from the three coordinate measuring machine u1

4.1 玻璃管的均匀性引入的测量不确定度u2

通过外径与厚度可计算得到玻璃管的内径,以计算得到的内径dcal与三坐标测量机测量得到的内径dmea的差值δ作为评估玻璃管均匀性的参数。由式(10)得到计算内径dcal为:

(10)

为了保证2种内径值相互独立,测量内径dmea仅取位于奇数位置的测量圆周的内径参与计算,如式(11)所示:

(11)

由式(10)和式(11)计算得到不同测量方法下内径的差值δ如式(12)所示:

(12)

玻璃管的壁厚测量结果如表2所示。

表2 玻璃管壁厚值hTab.2 The thickness of glass tube h mm

通过玻璃管壁厚h,由式(10)、式(11)、式(12)计算dmea、dcal、δ如表3所示。可以发现:三根玻璃管的不均匀性带来的最大误差分别为4×10-5mm、9.1×10-4mm、5.2×10-4mm,其分布视为均匀分布。玻璃管的均匀性引入的测量不确定度如表4所示。

表3 测量内径与计算内径比较Tab.3 The comparison between the measured value and calculated value mm

表4 玻璃管均匀性带来的不确定度u2Tab.4 The uncertainty resulted from glass tube uniformity u2

4.3 玻璃管的圆度引入的测量不确定度u3

如图6(b)所示,每个坐标点到理想圆圆心的距离为Lm,理想圆的半径为R,则坐标点到理想圆的距离为:

em=Lm-R

(13)

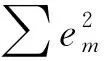
(14)

由于玻璃管内壁形状的不规则,这种偏差不会完全消失,所以圆度带来的最大允许误差为各个测量圆周圆度的平均值,为均匀分布。

表5所示为名义内径140 mm玻璃管的5个测量圆周为例的圆度和最大允许误差的计算。玻璃管的圆度引入的测量不确定度如表6所示。

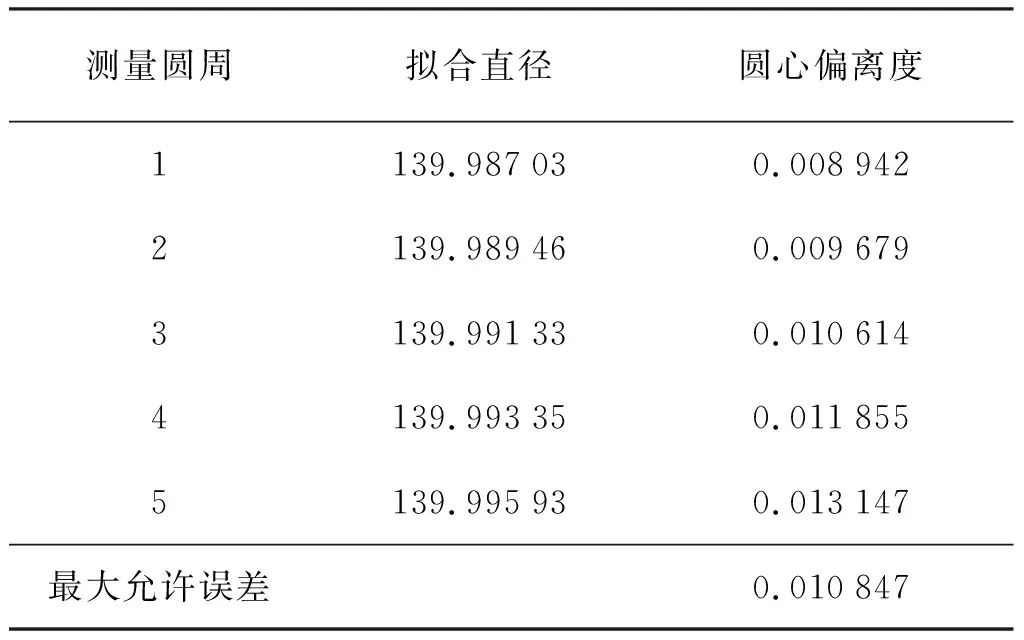
表5 圆度计算示例Tab.5 The example of roundness mm

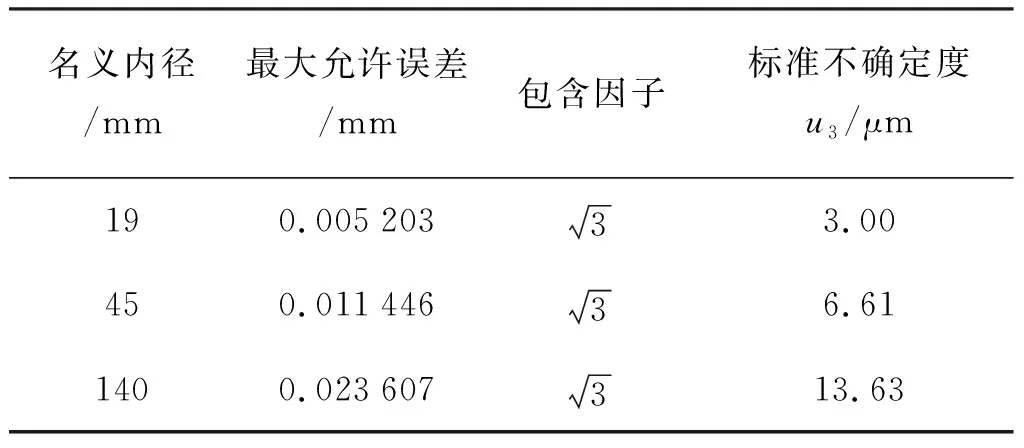
表6 圆度带来的不确定度u3Tab.6 The uncertainty resulted from the roundness u3

4.4 测量重复性u4

平均值的实验标准差可由式(15)计算,计算结果如表7所示。

(15)

表7 测量重复性u4Tab.7 The repeatability u4

内径测量的合成不确定度由式(16)计算,基于第3.1～3.4节的分析,活塞缸内径及测量不确定度如表8所示。

(16)

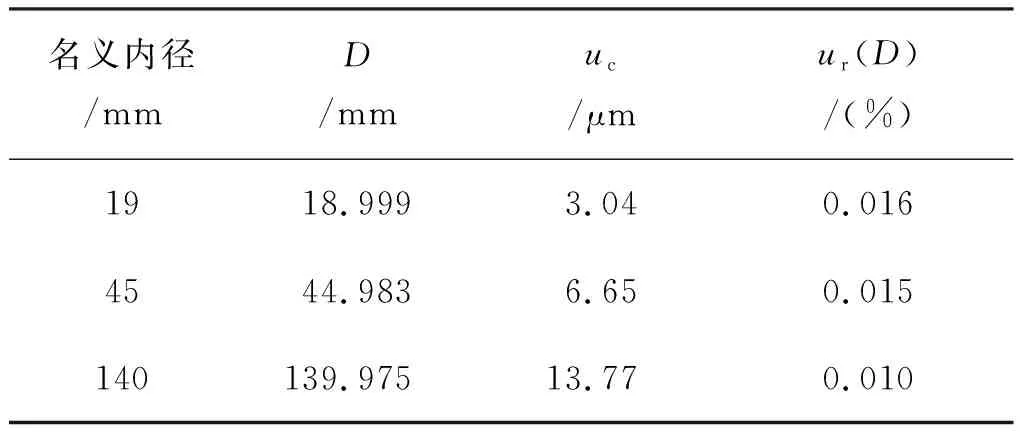
表8 活塞缸内径及测量不确定度Tab.8 The inner diameter and measurement uncertainty of piston cylinder

综上，针对名义内径分别为19 mm、45 mm、140 mm的活塞缸,内径测量结果分别为18.999 mm、44.983 mm、139.975 mm,测量相对不确定度分别为0.016%、0.015%、0.010%。

5 结 论

活塞缸的内径是活塞式气体流量标准装置测量不确定度的最主要来源。针对活塞缸自身结构特点对测量器具的限制,提出了三坐标测量机测量活塞缸内径的方法。

根据活塞缸的加工工艺,用两端内径的平均值作为活塞缸整体的内径,通过分析不同测量方法得到的活塞缸内径的差异,验证了三坐标测量机测量活塞缸内径的可靠性。

在活塞缸内径测量结果的不确定分析中,详细考虑了活塞缸内表面形状特征,即均匀性、玻璃管圆度等参数对标准装置的影响。

实验结果表明，为满足高准确度气体小流量溯源的需求，三坐标测量机测量被动式活塞气体流量标准装置的活塞缸内径是可行的。