基于膜计算的煤矿井下机器人路径规划算法
2021-11-30黄友锐李静韩涛徐善永
黄友锐, 李静, 韩涛, 徐善永
(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)
0 引言
煤矿井下空间狭小,环境恶劣,危险性大,对煤炭自动化采掘和运输提出了巨大挑战[1]。使用机器人进行煤矿井下生产和运输工作,可最大程度地减少伤亡事故。随着研究不断深入,机器人将被应用于煤矿井下探测、开采、运输、救援等工作[2],而要实现这些应用,机器人需能够在井下复杂环境中规划出合理、高效的可行路径。因此,路径规划成为煤矿机器人研究的重点之一。
路径规划的基本任务是寻找一条从起始点到目标点的可行路径[3],要求过程简单、用时少、寻找到的路径无碰撞且距离短等。路径规划算法一般分为基于栅格的路径规划算法和基于采样的路径规划算法[4]。基于栅格的路径规划算法包括Dijkstra及其改进算法等[5-7],这类算法具有过程简单、实时性好的优点,但路径规划效果过度依赖于划分地图栅格时所采用的分辨率。基于采样的路径规划算法不需要对环境进行离散化或对障碍物进行公式化处理,为路径规划提供了新思路。基于随机采样的快速扩展随机树(Rapidly-exploring Random Tree,RRT)近年来受到了极大的关注与重视[8-10],RRT算法具有建模快、搜索能力强的优点。文献[11]提出了具有渐进最优性的RRT*算法,解决了RRT算法无法收敛至最优路径的问题。针对RRT*算法采样范围过大、效率低的问题,文献[12]提出了Informed RRT*算法,在路径优化过程中的采样区域为椭圆形,相比于RRT*算法对整个空间进行搜索来讲,缩小了采样空间,加快了收敛速度。但基于采样的路径规划算法采用随机采样、固定步长增长树的方式生成路径,规划时间长、效率低。
为了加快路径规划速度,研究者们提出了多种算法融合的路径规划方法,如A*与RRT融合[13]、人工势场与RRT融合[14]、贪婪策略与RRT*融合[15]、三角不等式与RRT*融合(PQ-RRT*)[16]、启发式偏差与RRT*融合[17]等。这些融合算法优化了全局最优解的搜索过程,加快了搜索速度,但仍都采用固定步长和串行计算的规划方式,在一些复杂环境中,尤其是煤矿井下狭小空间环境中,容易产生路径规划失败、规划速度慢、规划路径不合理等问题。
膜计算(Membrane Computing,MC)是一种通过编写规则处理类细胞或类组织中多个对象的分布式并行计算仿生模型。多个基本膜同时独立进行规则更新,使得MC具有很强的分布式和并行性计算特点,在处理工程优化问题上具有独特优势。因此,本文利用MC改进Informed RRT*算法,提出了一种基于MC的煤矿井下机器人路径规划算法,即基于MC的Informed RRT*(MC-IRRT*)算法。该算法充分利用了多核计算机的并发计算能力,使细胞型膜结构中的多个基本膜能并行工作(不同步长、多采样点),既可以在大空间区域进行大步长快速搜索,也可以在小空间区域进行小步长精细搜索,扩大了采样范围,在控制搜索时间的前提下,增强了路径优化能力,特别适用于煤矿井下狭长空间的特殊环境。
1 MC和Informed RRT*算法
1.1 MC


图1 细胞型膜系统结构
MC的核心思想是在多个基本膜内根据各自规则同时更新对象,并将更新结果输送到表层膜,表层膜再根据自己的规则进行计算和更新,并输出最终结果。
1.2 Informed RRT*算法
Informed RRT*算法是一种基于采样的路径规划算法,算法分为2个阶段:第1阶段,采用RRT算法在整个地图中随机采样,并用固定步长增长树的方式快速寻找到一条从起始点到目标点的可行路径;第2阶段,根据已经获取的可行路径,在1个特定的椭圆区域内采样,获取新的可行路径,不断优化找到的可行路径,最终找到一条最短的可行路径作为路径规划结果。
Informed RRT*算法路径优化过程中的采样区域为椭圆形,其搜索过程如图2所示。

图2 Informed RRT*算法搜索过程
与RRT*算法相比,Informed RRT*算法的采样空间不断缩小,其收敛速度也相应加快,搜索效率提升。但Informed RRT*算法的第1阶段是以固定步长不断获取路径点,生成可行路径,若步长过大,则不能寻找到较窄路径;若步长较小,则搜索速度变慢。第2阶段则以串行方式搜索路径并进行比较后才能确定最优路径,效率较低。
2 MC-IRRT*算法
2.1 算法总体结构
MC-IRRT*算法的总体结构如图3所示。
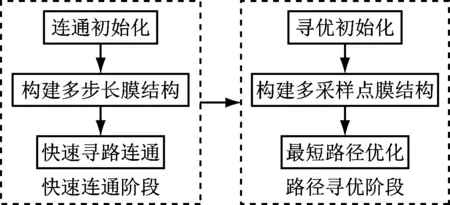
图3 MC-IRRT*算法总体结构
MC-IRRT*算法主要包括快速连通和路径寻优2个阶段。在快速连通阶段,构建具有多个步长的细胞型膜结构,多个基本膜分别以不同的步长进行搜索,在表层膜中进行筛选优化,不断迭代,最终找到一条从起始点到目标点的可行路径。在路径寻优阶段,构建具有多采样点的细胞型膜结构,多个基本膜分别生成多个不同采样点,不断搜索更优路径,最终找到最短可行路径。
2.2 快速连通阶段
MC-IRRT*算法快速连通阶段构建的多步长膜结构如图4所示。
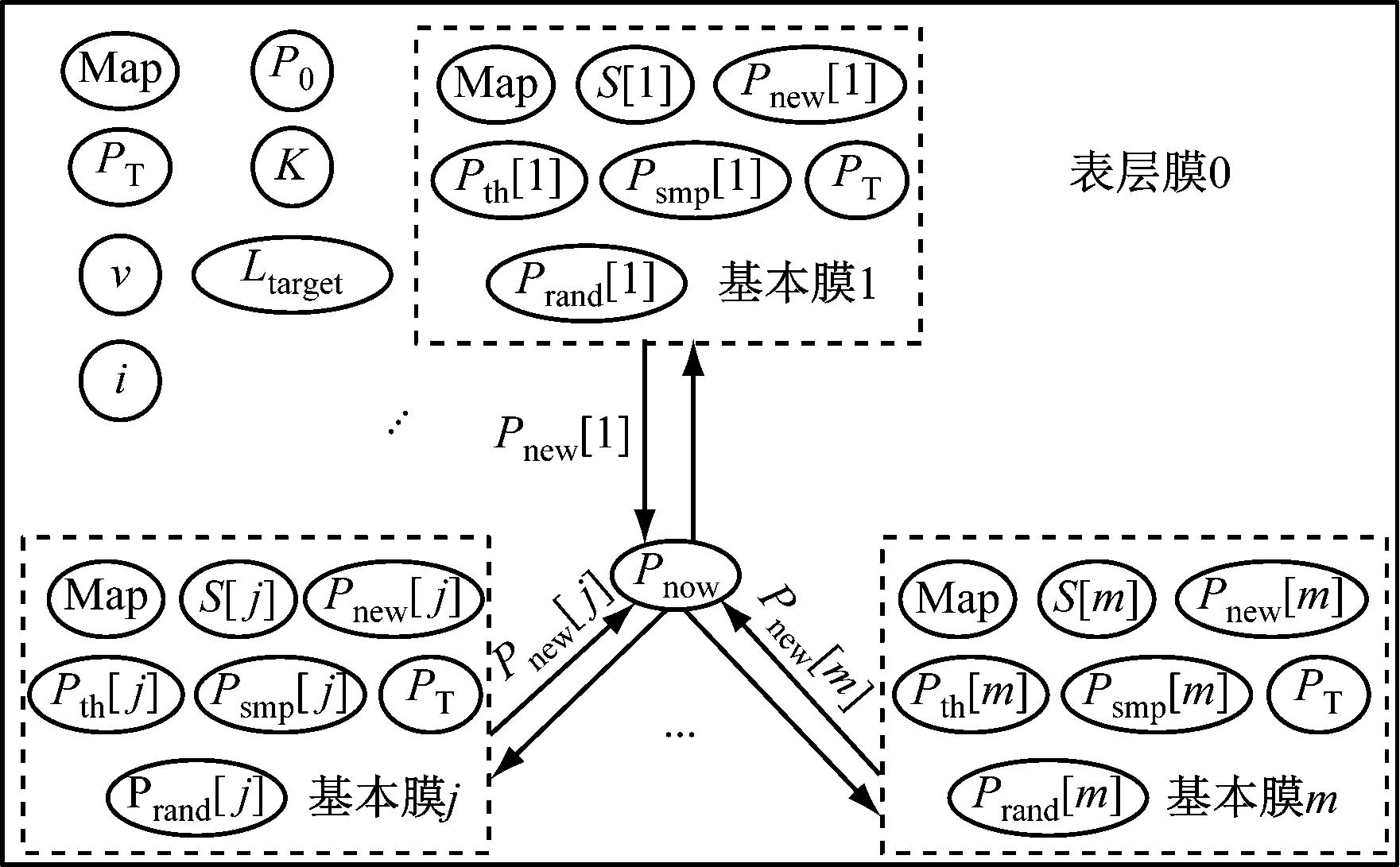
图4 多步长膜结构
多步长并行膜结构可描述为
Π=(V,T,u,w0,w1,…,wm,R0,R1,…,Rm)
(1)
(2)
u=[0[1]1,…,[j]j,…,[m]m]0
(3)
w0={Map,P0,PT,K,ν,i,Ltarget}
(4)
(5)
式中:V为系统中所有元素的集合;T为输出对象的集合,T⊆V;u为膜系统,含有m个基本膜和1个表层膜(表层膜0);wj表示膜系统u中基本膜j内包含的字符对象;Rj为基本膜j的运行规则;Map为区域地图信息;P0,PT分别为起始点位置坐标和目标点位置坐标;K为迭代次数;ν为路径点集合;i为当前迭代次数;Pnow为当前路径点集合;S为采用步长集合;Pth为随机采样概率阈值集合;Psmp为采样点集合;Pnew为新路径点集合;Prand为随机采样点集合;Ltarget为新路径点到达目标点的距离阈值;[j]表示基本膜j中对应的粒子对象。
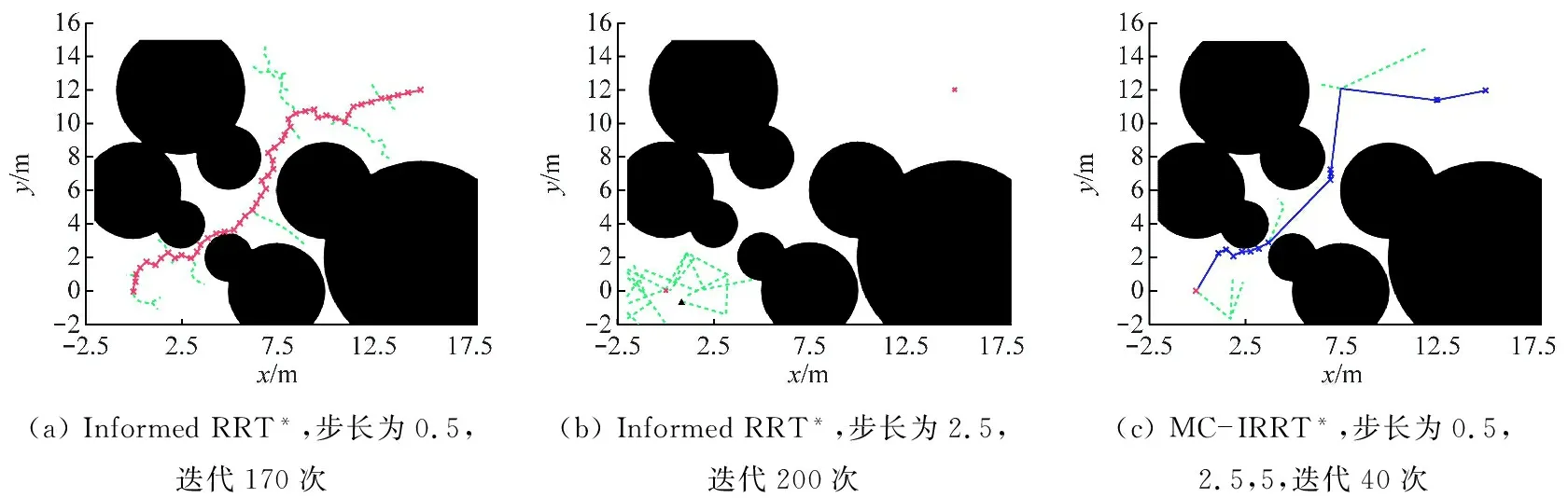
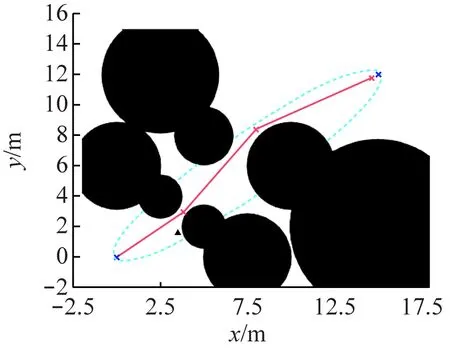
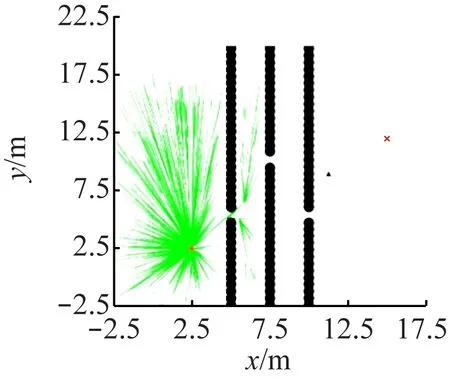
基本膜j的运行规则:① 在区域地图Map中随机采样1个点Prand[j],比较该点与随机采样概率阈值的大小。如果Prand[j]≥Pth[j],则基本膜内采样点就是Prand[j];如果Prand[j] 表层膜0的运行规则:分别计算m个基本膜输出的新节点Pnew[j]与目标点PT之间的距离L[j],并选取最小值。 (6) Lmin=minL[j] (7) 将距离PT最近的节点作为新的路径点加入到路径点集合ν中,再将该节点作为当前迭代次数寻找到的路径点,重新同时输入到m个基本膜中,不断迭代循环,直至找到目标点。当满足以下条件时认为目标点被找到。 (8) 式中Lnow为当前路径点与目标点的距离。 判断Lnow是否在阈值范围内,如果Lnow≤Ltarget,说明寻找的路径已经到达目标点,将输出的所有路径点按顺序连接起来,即可得到一条起始点到目标点的可行路径。如果Lnow>Ltarget,说明此时找到的路径点不是目标点,进行下一次迭代循环,直到满足最大迭代次数为止。 快速连通阶段工作流程如图5所示。 图5 快速连通阶段工作流程 (1)设置表层膜0的当前路径点Pnow=P0,当前迭代次数i=1,路径点集合ν={P0}。 (2)将当前路径点Pnow复制到m个基本膜内,同时进行基本膜计算,得到m个新路径点Pnew[j],将其输出到表层膜0中。 (3)表层膜0分别计算每个新路径点与目标点之间的距离,获取距离最小值对应的新路径点,将其作为当前迭代次数寻找到的路径点放入到路径点集合ν中。 (4)计算当前路径点与目标点的距离,判断是否到达目标点,到达则跳转到步骤(6),否则跳转到步骤(5)。 (5)判断迭代次数是否完成,即i是否等于K,若是,则认为迭代完成,跳转到步骤(6);否则,令i=i+1,跳转到步骤(2)。 (6)快速连通结束,输出路径点集合ν,按顺序连接路径点集合中所有路径点,作为寻找到的起始点到目标点的一条可行路径。 快速连通阶段采用多步长膜结构,能够根据空间区域的大小来调整步长。在可行空间较大的区域采用大步长搜索,加快搜索速度,而在狭小的空间使用小步长搜索,使搜索空间更加精细,提高狭小空间路径搜索成功率,保证煤矿机器人在煤矿复杂多变的环境中安全高效行驶。 路径寻优阶段的主要目的是基于快速连通阶段已经找到的一条可行路径,进行最短路径优化,从而寻找出从起始点到目标点之间的最短可行路径。将MC的并行性和高效性与Informed RRT*算法相结合,在第1阶段寻找到一条从起始点到目标点的可行路径后,形成1个椭圆采样区,然后通过构建多采样点膜结构,让m个基本膜同时在椭圆区域内并行搜索最短可行路径。 构建多采样点并行膜结构,如图6所示。 图6 多采样点并行膜结构 多采样点并行膜结构可描述为 (9) (10) u′=[0[1]1,…,[j]j,…,[m]m]0 (11) (12) (13) 表层膜0的运行规则:表层膜0根据Map,P0,PT和当前路径长度形成1个椭圆形采样区域M,如图7所示。椭圆的2个焦点为P0和PT,2个焦点之间的距离为Cfocus,当前路径长度为椭圆的长轴Clong,Cshort为椭圆的短轴,具体计算公式为 图7 采样椭圆 (14) Pi∈ν′ (15) (16) 路径寻优过程: (1)将寻优路径点集合ν′[0]设置为快速连通阶段找到的路径点集合ν,即ν′=ν,当前迭代次数i[0]=1。 (2)表层膜0根据区域地图信息、起始点、目标点和寻优路径点集合形成1个椭圆形区域作为随机采样区M,并输入到所有基本膜中。 (3)m个基本膜分别同时按照Informed RRT*椭圆区域寻优过程进行计算,并将得到的路径点集合ν′[j]输出到表层膜0。 (4)表层膜0分别计算当前路径点集合ν′[0]和ν′[j]内路径点距离之和,选取最小值对应的路径点集合作为新的最短路径点集合,即ν′[0]=min{ν′[0],ν′[j]}。 (5)判断迭代是否完成,即i[0]是否为N[0],若是,则认为迭代完成,跳转到步骤(6);否则,令i[0]=i[0]+1,跳转到步骤(2)。 (6)最短路径优化结束,输出ν′[0],即起始点到目标点的最优可行路径。 路径寻优流程如图8所示。 图8 路径寻优流程 路径寻优阶段的优点是采用了多采样点膜结构,通过m个基本膜的并行计算,能够同时在多个椭圆区域内并行搜索最短可行路径,节省了时间,提高了路径优化效率,可在最短时间内找到一条起始点到目标点的最优路径,大大增强了机器人路径规划的实时性,提高了机器人的行驶效率,为机器人在煤矿井下自主安全行驶提供了基础保证。 为了验证所提算法的有效性,在不同场景进行对比实验。实验硬件系统为Intel(R)Core(TM)i5-7500 CPU@3.80 GHz,内存为(RAM)16 GB,软件采用Python 3.6编程。实验分为2个场景,如图9所示,场景1为简单环境,地图大小设置为20 m×20 m,图中x,y分别为地图的横坐标和纵坐标,黑色代表障碍物,不能通行,白色区域为可行区域,环境布置时尽量在起始点和目标点之间的路径与周围障碍物之间留下狭小的空间,主要分析改进算法2个阶段的运行性能。煤矿井下空间狭小,加上大型生产设备,很容易出现连续狭小的极端环境,为了模拟煤矿井下环境,设计了场景2,地图大小为22.5 m×22.5 m,黑色障碍物中间只留了距离为2 m的可通行区域,且连续设置3个可行区域不在一条直线的障碍物,以测试苛刻环境下的路径规划效果。场景1和场景2的起始点分别为(0,0)和(2.5 m,2.5 m),目标点都为(15 m,12 m)。 (a)场景1 在场景1中,使用MC-IRRT*算法和InformedRRT*算法进行对比实验,测试MC-IRRT*算法的特性。在快速连通阶段,考虑到采用的CPU为四核,设置多步长膜结构为1个表层膜(表层膜0)、3个基本膜(基本膜1、基本膜2和基本膜3),3个基本膜的步长分别设置为0.5,2.5和5,Informed RRT*算法在步长为0.5和2.5的条件下运行,算法最大迭代次数为200。2种算法的实验结果如图10所示。 图10 快速连通阶段实验结果对比 由图10(a)可知,Informed RRT*算法在步长为0.5时运行了170次,规划出一条可行路径,可以成功搜索到一条起始点到目标点的路径,但由于步长很小,需要多次迭代才能最终找到可行路径。由图10(b)可知,增大步长后Informed RRT*算法没能到达目标点,快速连通失败,由于步长较大,很难搜索到较狭小的可行空间,最大迭代次数200次运行结束后,也很难找到一条可行路径。由图10(c)可看出,由于改进算法在此阶段采用了多步长并行膜结构,在狭小区域选择小步长,能够顺利搜索到可行路径,在较大可行空间选择大步长,可以加快搜索速度,因此,在迭代40次之后便成功搜索到了一条从起始点到目标点的可行路径。相比于Informed RRT*算法,MC-IRRT*算法减少了130次迭代,搜索效率提高了76%。 在路径寻优阶段,由2种算法得到的实验结果如图11所示。对比图11(a)和图11(b)可看出,在迭代次数相同的情况下,MC-IRRT*算法得到的路径更短,这是因为其在路径寻优阶段使用了多采样点膜结构,利用MC的并行性,3个基本膜同时进行采样搜索,再与表层膜进行信息粒子交换。对比图11(a)和图11(c)可看出,在找到相同优化路径的条件下,Informed RRT*算法需要迭代200次,而MC-IRRT*算法只需要迭代120次,路径寻优搜索效率提高了40%。 (a)MC-IRRT*,迭代120次 为了进一步验证MC-IRRT*算法性能,选择可通行路径更加苛刻的场景2进行实验,并与RRT*,Informed RRT*和PQ-RRT*算法进行对比,4种算法均设置迭代次数为3 000次,实验结果如图12所示。从图12可看出:在迭代满3 000次后,RRT*和Informed RRT*算法都无法找到一条从起始点到目标点的可行路径;PQ-RRT*算法成功寻找到了可行路径并有所优化,但由于使用的是固定步长增长树,寻找到的路径不够平滑;MC-IRRT*算法由于使用了多步长,不仅可以迅速通过较窄可行区域,而且在路径转折处可以选择使用较小步长,使路径更加平滑。 (a)RRT* 复杂场景具体实验数据见表1。可以看出,PQ-RRT*算法和MC-IRRT*算法均能成功寻得可行路径,PQ-RRT*算法平均用时17.05 s,而MC-IRRT*算法平均用时14.87 s,比PQ-RRT*算法少用了2.18 s,速率提高了12.79%。从寻到的平均路径长度可以看出,MC-IRRT*算法规划的路径长度比PQ-IRRT*算法规划的短8.18%。 表1 复杂场景具体实验数据 (1)提出了一种基于MC的煤矿井下机器人路径规划算法,将MC的并行性与Informed RRT*算法相结合,使用多步长并行计算,既可以使用大步长进行快速搜素,也可以采用小步长精细搜索,增加了在狭长空间中的搜索成功率,提高了搜索效率。使用多采样点同时采样搜索,在不大幅增加运行时间成本的前提下,扩展了采样区域,提高了路径优化效率。 (2)简单场景实验结果表明,与Informed RRT*算法相比,MC-IRRT*算法在快速连通阶段和路径寻优阶段的搜索效率分别提高了76%,40%。复杂场景实验结果表明:RRT*算法和Informed RRT*算法路径规划失败,PQ-RRT*算法和MC-IRRT*算法均能成功寻得可行路径;与PQ-RRT*算法相比,MC-IRRT*算法的速率提高了12.79%,规划的路径长度缩短了8.18%;MC-IRRT*算法不仅可以迅速通过较窄可行区域,而且在路径转折处可以选择使用较小步长,使路径更加平滑。 (3)MC-IRRT*算法充分利用了多核CPU的并行运算能力,极大提高了路径规划的效率和实时性,为煤矿井下特殊环境下机器人的自主行驶提供了可靠保证。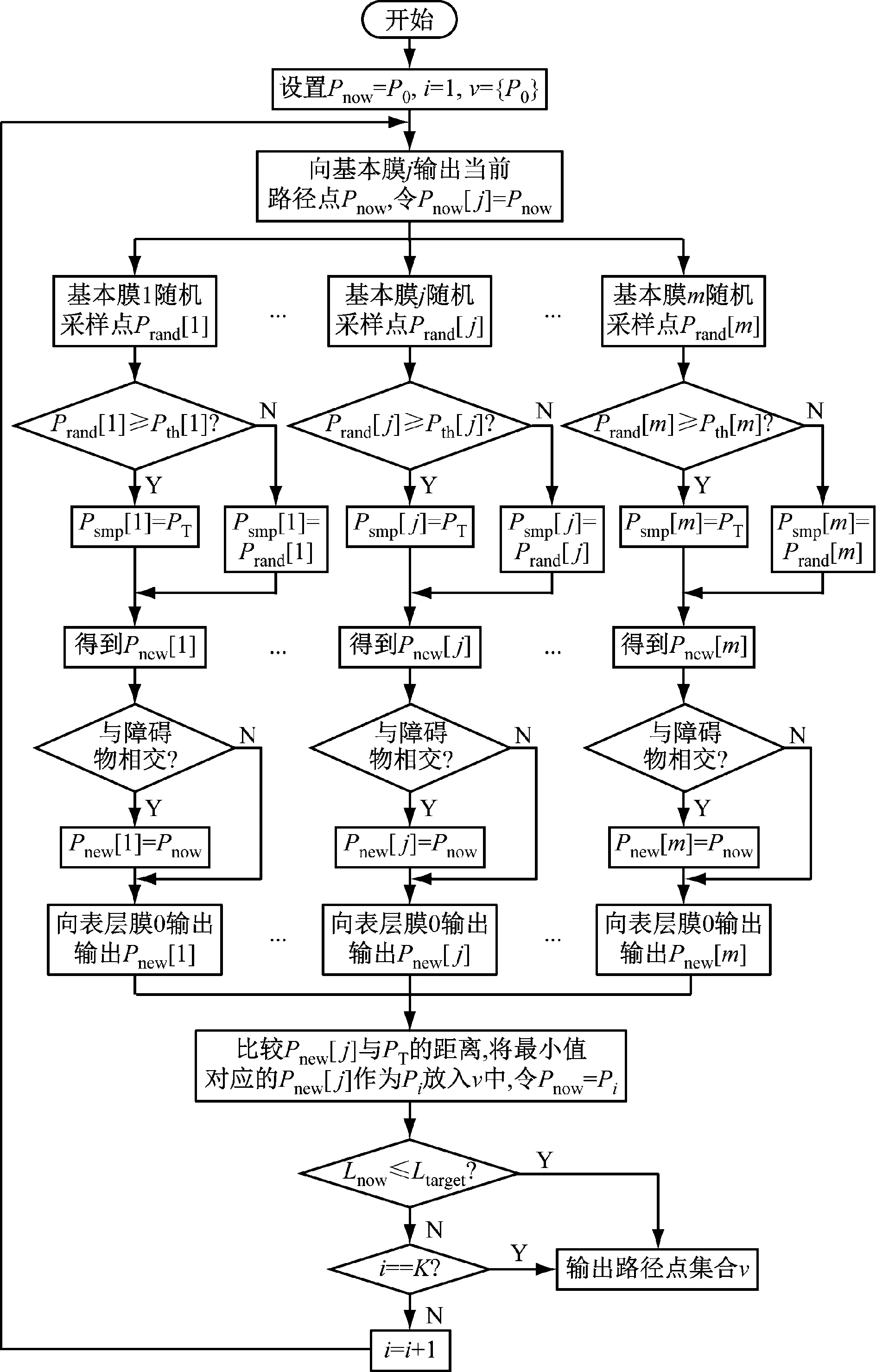
2.3 路径寻优阶段





3 实验分析
3.1 实验条件

3.2 简单场景实验
3.3 复杂场景实验

4 结论
