基于FAST-MCD算法的异常成绩检测研究

孙杰

（中国劳动关系学院应用技术学院，北京100044）

0 引言

在教学过程中，难免对学生进行知识学习效果的检测。在理想情况下，学生的测验成绩是稳定的、平稳的，但在实际情况下难免出现异常成绩情况，这些异常成绩情况恰好体现了某些学生在学习过程中的问题及存在的风险。有效检测学生成绩中的异常成绩，能够及时地发现问题，指导教师教学。

假设在任何一次测验中所有同学的测验成绩符合正态分布，且同一个学生在一次测验中的成绩排名是基本稳定的。本文采用2016级至2019级本科生共465人的两次平时测验成绩作为数据样本。通过对所采集数据样本的观察发现：在测验成绩中，有的同学没有参加测验或成绩远低于正常成绩。这种情况恰恰说明，某些同学学习过程中可能存在一定的问题。这些学生成绩数据与一般的测验成绩的高低或特征不一致，这些数据对象就是孤立点（outlier）。当训练数据集没有孤立点污染时，通过训练数据集构造模型，通过模型判断新加入的点是否满足要求（一般通过阈值判断），不满足条件的点称为异常点（novelty）。孤立点和异常点的检测和分析是一种十分重要的数据挖掘类型。

基于高斯概率密度函数的异常点检测，首先利用异常较少的数据集拟合出一个高斯分布，当要预测一个样本是否为异常时，只需将这个新样本代入高斯分布求出概率，如果概率小于指定的阈值，我们就认为这个样本是异常的。因此，异常点检测的关键是训练数据集的收集和阈值的设定。孤立点的检测不要求用于拟合模型的数据纯净，孤立点的检测有基于统计学的方法［1］、基于聚类的方法［2］、One Class SVM算法［3］和孤立森林算法［4］等多种。本文基于已有学生成绩满足高斯分布的假设，试图采用FAST-MCD算法对上述异常成绩进行检测，通过构建限度椭圆检测学生测验成绩中的异常成绩。

1 异常成绩检测模型［5］

n维正态向量X=(X1,X2,…,Xn)T的密度函数为：

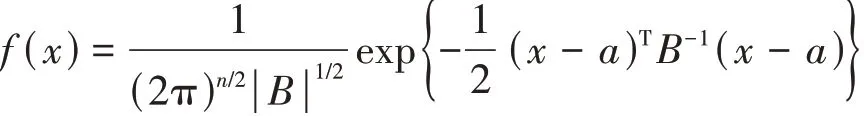
其中，

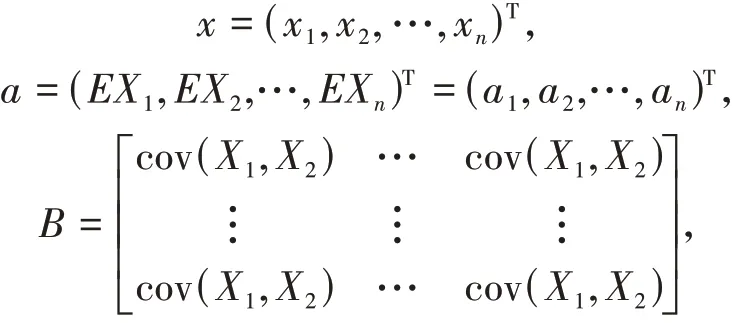
且矩阵B正定的。此时

假设一组有n个样本的数据，每个样本有p个元素，数据构成X=(x1,x2,…,xp)T，其中，xi=(xi1,xi2,…,xip)T,i=1,2,…,n。经 典 的 限 度 椭 圆（Tolerance Ellipse）定义为一组p维数据x，其马氏距离计算如下：

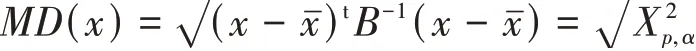
其中xˉ为均值，B是协方差矩阵，卡方分布的α分位数。

实验证明：基于马氏距离的限度椭圆模型并不能很好地估计孤立点，而基于鲁棒距离（the robust distances）的计算方法获取的限度椭圆模型可以较好地辨识孤立点。鲁棒距离的计算方法如下：

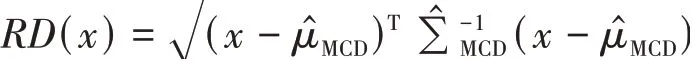
FAST-MCD算法的步骤如下：

（1）假设有n个样本的样本集X，选取其子集H1，且而和分别是子集H1的均值和协方差。如果子集则有n个样本中每个元素到子集H1的距离：

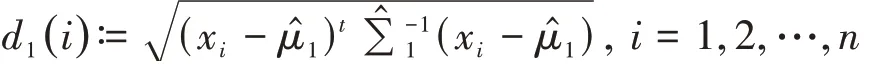
3 实验结果

实验运行在Windows系统中的“Anaconda 3+Python 3.7”环境下，采集选修《计算机I》课程的465名同学的两次平时测验成绩为样本点，其中包含异常成绩，所占比例大约为10%。异常成绩包含未参加考试的成绩为0或者远离一般成绩范围的成绩。

本文实验中分别使用经验协方差（最大似然估计）和鲁棒协方差（最小协方差估计）两种方法对两次学生测验成绩中的孤立点（或称为异常成绩）进行检测，两次测验成绩中的异常成绩检测结果，如图1所示。

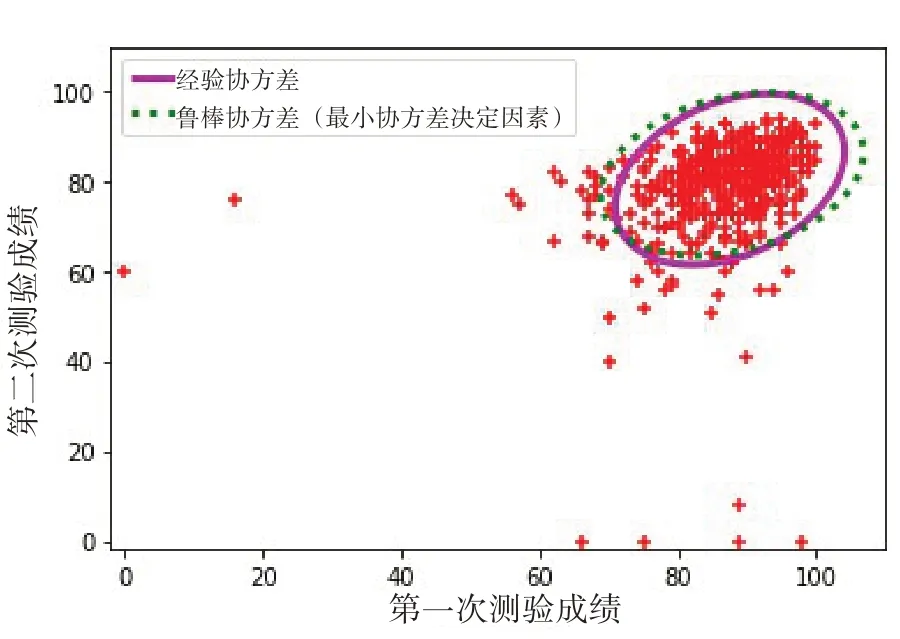
图1 学生两次测验成绩中的异常值检测

可以看出，两次测验成绩中只要有一次成绩较低（或为0），或者两次测验成绩均较低，即可视为异常成绩。另外，虽然经验协方差方法更容易被离群点影响［5］，但在异常成绩比例为10%时，两种检测方法在成绩检测的最终效果上并没有太大的差别。

本文实验中设置异常成绩比例为10%，最终筛选出47个点为异常点。删除异常成绩后两次测验成绩的散点图，如图2所示。

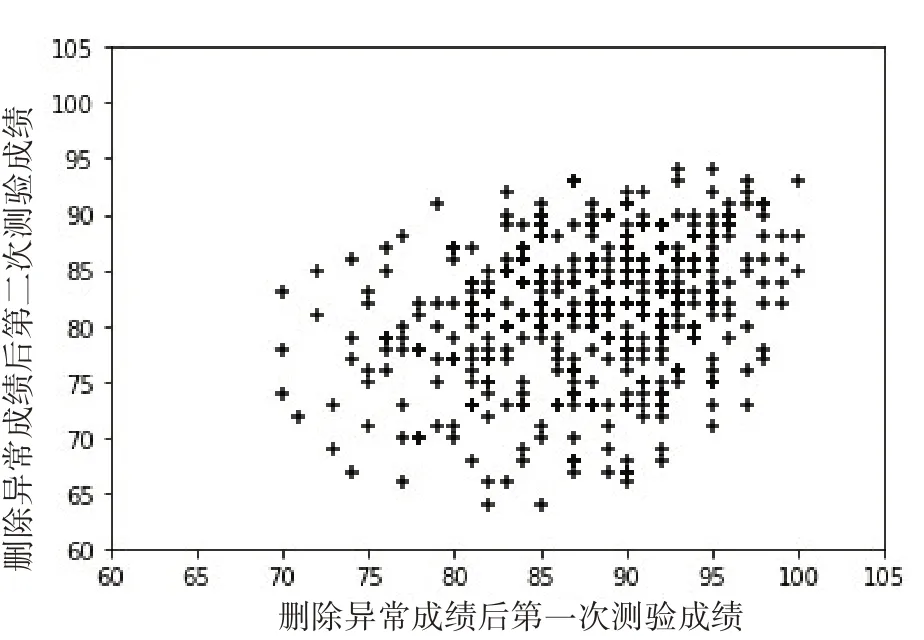
图2 删除异常成绩后两次测验成绩的散点分布

可以看出，在删除异常成绩之后，学生成绩分布更集中，学生两次测验成绩集中在70～100和65～95之间的数据区域。

当设定成绩异常比例为1%时，检测结果如图3所示。

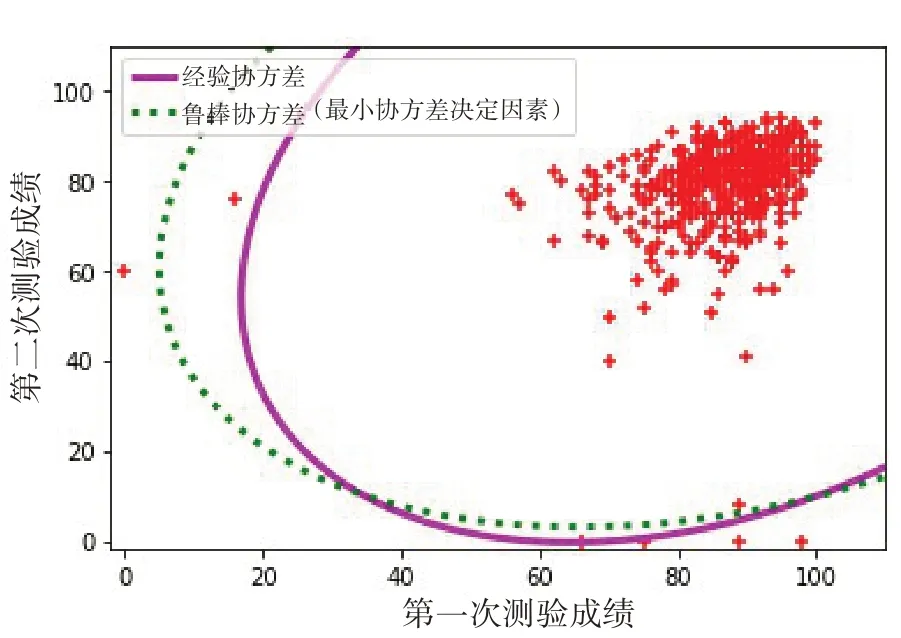
图3 学生两次测验成绩中的异常值检测

可以看出，通过鲁棒协方差方法得到的限度椭圆完全划分出了其中一个成绩为0的5个数据点，而经验协方差方法却将第二次测验成绩为0的一个数据点认为是正常的。这也说明鲁棒协方差方法具有更好的稳定性，能够较为合理地检测异常成绩。

4 结语

最小协方差估计（MCD）是能够较好地识别样本集中的异常点，但由于计算较为复杂，我们采取FAST-MCD算法简化计算过程。通过实验发现，FAST-MCD方法能够较快、较稳定地检测出异常成绩。但本文实验存在一些不足，如依据经验给出的异常成绩的比例比较随意，缺少理论依据。因此，在将来的研究中，希望能够依据实际采集的样本值自适应得到异常数据的比例。