基于混合策略的缎蓝园丁鸟优化算法
2021-11-30曹灿高鹰李宁郭晓语
曹灿,高鹰,李宁,郭晓语
(广州大学计算机科学与网络工程学院,广州510000)
0 引言
启发式算法是一种基于直观或经验,利用类似仿生学的原理,根据自然、动物中的一些现象而抽象成的算法[1]。对于非确定性多项式难度问题,是无法求解到最优解的,因此,使用启发式算法是一种较好的选择,去尽可能逼近最优解,得到一个相对优解。因为启发式算法具有简单直观、易于修改、处理问题较快,且能够在可接受的时间内给出一个较优解等特点,被广泛运用于生产生活中的各种优化问题中。常见的启发式算法有蚁群算法(ant clony optimization,ACO)、模拟退火法(simulated annealing,SA)、神经网络算法(neural network algorithm,NNA)、粒子群算法(particle swarm optimization,PSO)、遗传算法(ge⁃netic algorithm,GA)、萤火虫算法(firefly algo⁃rithm,FA)等[2-7],虽然这些启发式算法的编码各种各样,但是它们的本质都是一样的,就是要求解出全局的最优解。如在PSO算法[8]中,把鸟看做粒子,模仿鸟类的捕食行为来寻找目标函数的最优值;在GA[9]中,通过模拟自然进化过程来搜索目标函数最优解;FA[10]模仿萤火虫之间的信息交流,萤火虫的位置代表了一个待求问题的可行解,萤火虫的亮度表示该萤火虫位置的适应度,通过寻找位置最亮的萤火虫来搜索目标函数最优解。
缎蓝园丁鸟算法(satin bowerbird optimization algorithm,SBO)是Moosavi等人[11]在2017年提出的一种启发式算法。其原理是模仿自然界中雄性缎蓝园丁鸟的求偶行为,且成功地应用在柔性交流输电和提高软件开发工作评估的准确性上,但目前国内外对其研究的文献不多。
本文提出了一种基于混合策略的SBO算法。改进了原算法中收敛速度过慢和收敛精度低的问题。采用Logistic混沌映射对种群进行初始化,使生成的初始种群伪随机性强,增加了种群的多样性,从而使初始种群分布更均匀;通过加入自适应权重,提升了算法的全局搜索能力,提高了求解的精度;改变原有的高斯变异,引入了Levy飞行变异,提升了种群分布的多样性,有利于算法跳出局部最优。
1 缎蓝园丁鸟优化算法
在自然界中,成年雄性园丁鸟在交配季节开始在自己的区域上建造求偶亭,它们利用各种各样的材料来吸引雌性园丁鸟;但是,并不是所有的雄鸟都能成功构建求偶亭,有的求偶亭会被破坏[12]。根据以上原理,可以将SBO算法分为以下5个阶段:
(1)随机生成初始种群。随机生成一个含有NB个个体的初始种群其中,NB为种群大小,D维数,t代表当前进化代数。
(2)计算每个个体的适应度值,然后计算出此适应度值在群体适应度值总和中所占的比例,表示该个体在选择过程中被选中的概率。每个个体被选中的概率,由等式(1)计算,其中fiti代表第i个求偶亭的适应度值,通过式(2)计算,f(xi)是第i个求偶亭的代价函数,即目标函数,通过公式(2)每次迭代保证代价函数的函数值不断减小:

(3)位置更新。根据雄性缎蓝园丁鸟的生活原理,对求偶亭的位置进行更新,如公式(3):
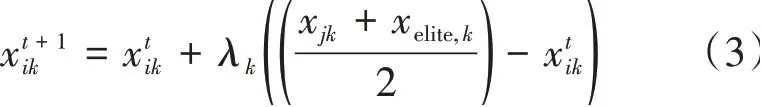

其中,α为步长的最大阈值;Pj是目标求偶亭的被选中概率,取值为0~1。当目标位置被选中概率越大时,步长越小;当目标位置被选中概率为0时,步长最大为α;当目标位置的被选中概率为1时,步长最小,为α/2。
(4)变异。根据雄性缎蓝园丁鸟的求偶亭会遭到破坏的自然现象,算法采取了一定的概率进行变异,如公式(5)和(6)所示:
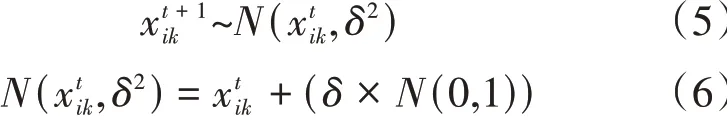
其中,xik服从正态分布,δ为标准差,通过公式(7)计算:
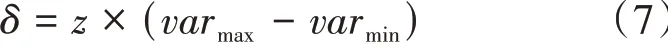
其中,z是缩放比例因子,varmax和varmin分别是变量xi的上限和下限。
(5)将旧种群和从变异中获得的种群进行组合。在每个周期的最后,对旧种群和从变异中获得的种群进行评价,合并对组合种群中的所有个体的成本函数值进行排序,保留函数值最小的个体,若此时满足终止条件,则输出最佳位置及其对应的最优值,否则继续进行步骤(3)~(6)。
SBO算法的伪代码设计如下:

2 改进的缎蓝园丁鸟优化算法
2.1 基于Logistic混沌映射的种群初始化
对于元启发算法而言,种群的初始化对算法的收敛速度和收敛精度有一定的影响[13]。在进行迭代寻优时,要尽可能使种群初始值在搜索空间分布均匀,来获得更高的全局搜索能力和种群多样性。在原算法中种群初始化是随机的,随机过程并不能保证初始种群能够分布均匀,种群位置随机分布,使得部分个体远离最优解,从而会影响算法的收敛速度。为了解决原算法中存在的这些问题,引入了logistic混沌映射。
混沌是存在于非线性系统中的一种普遍现象[14]。由于混沌运动的遍历性,规律性和伪随机性等,它能够在一定的范围内不重复的经历所有状态,而又不会失去种群初始化的随机性,正是由于这些特点,采用混沌搜索比其他随机搜索更具有优越性。基于混沌序列的思想,本文采用一种Logistic混沌映射,这是一种比较常用的混沌序列,其表达式如下:
x(t+1)=ux(t)(1-x(t))t=0,1,2,…,n(8)其中,u是混沌参数,t是迭代次数。
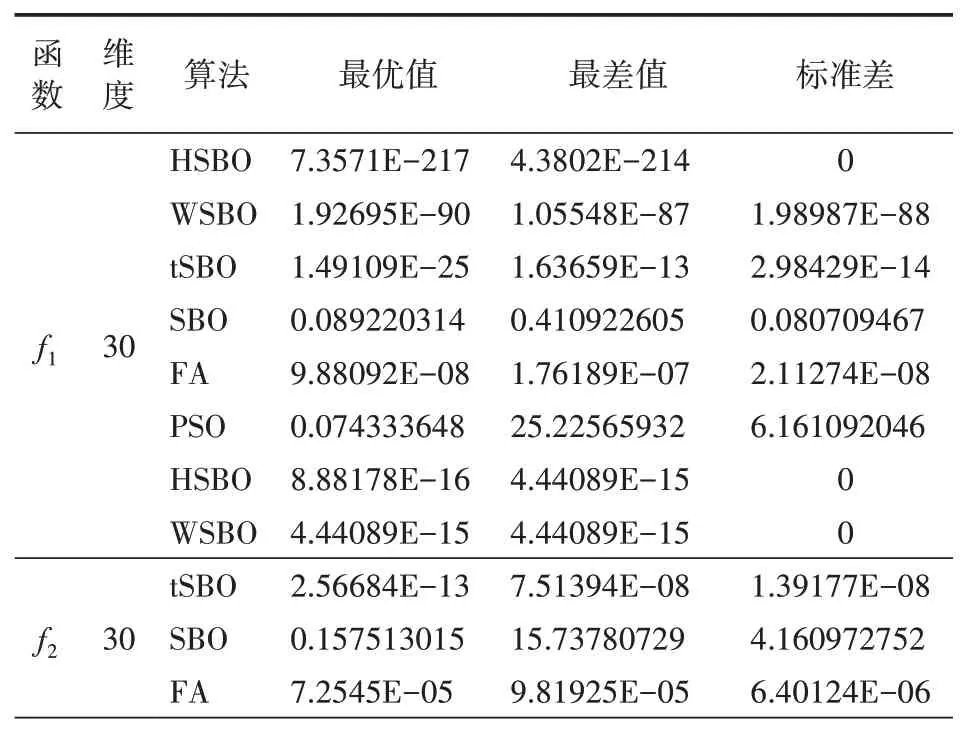
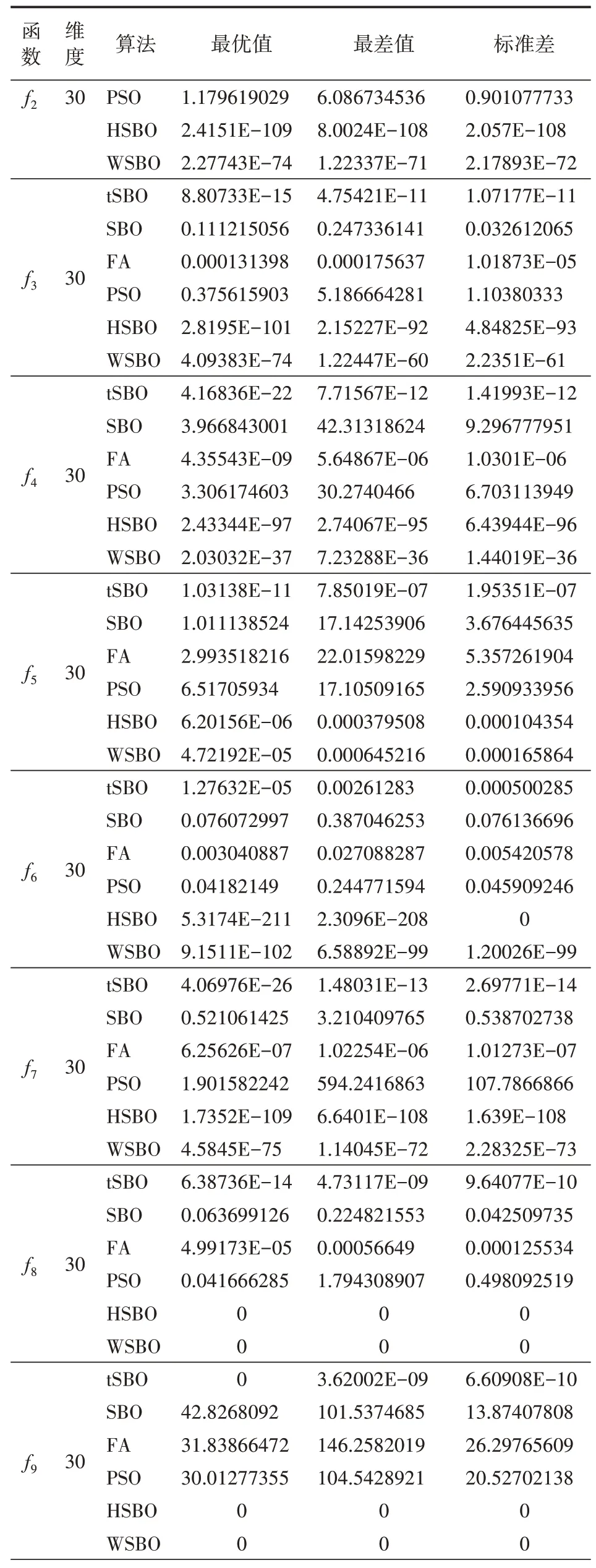
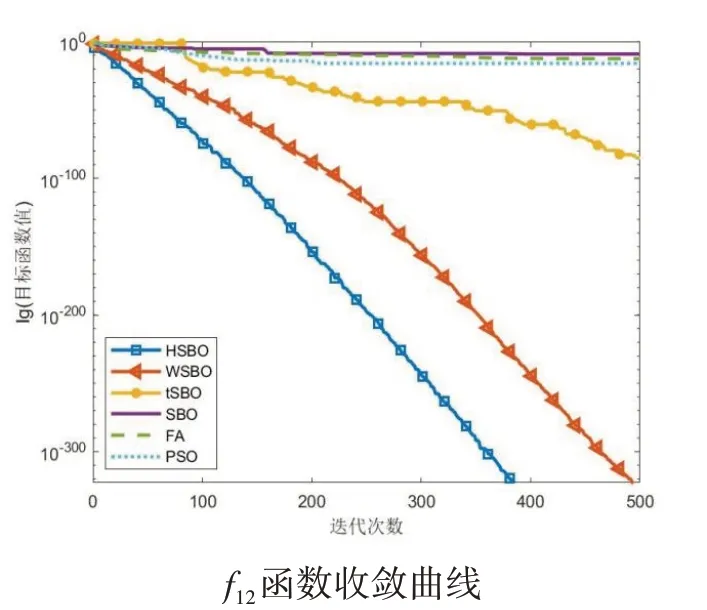
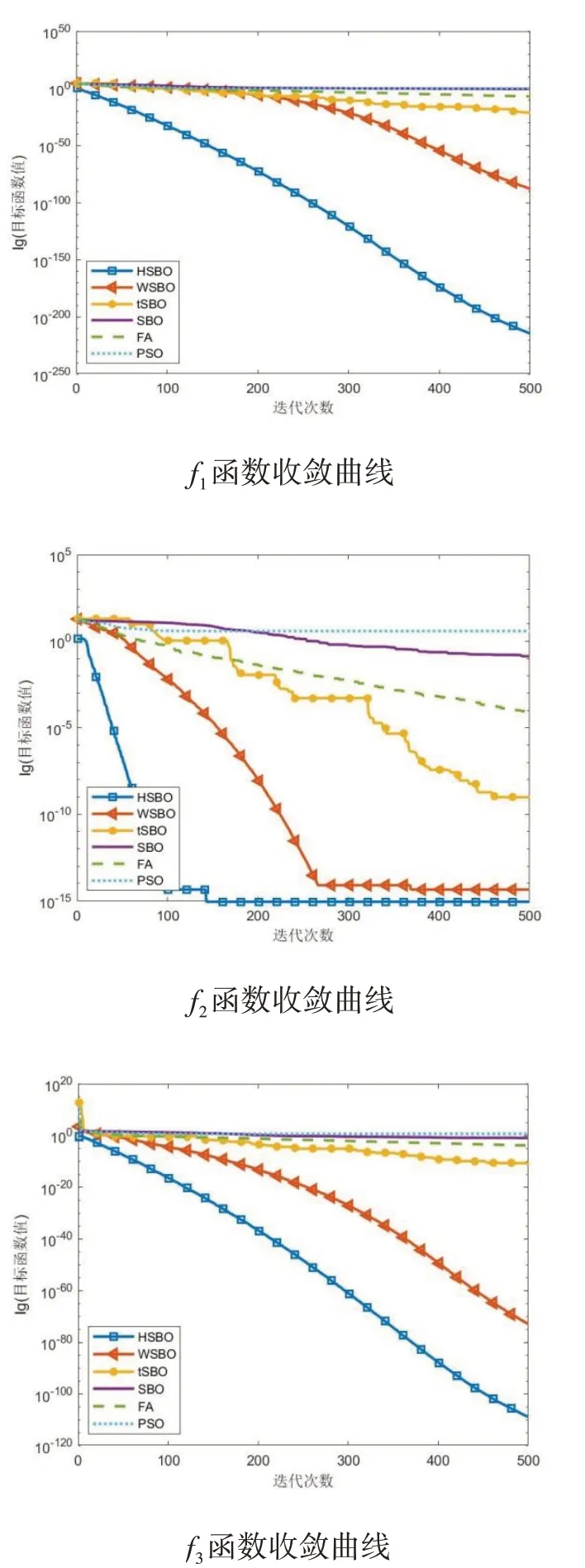
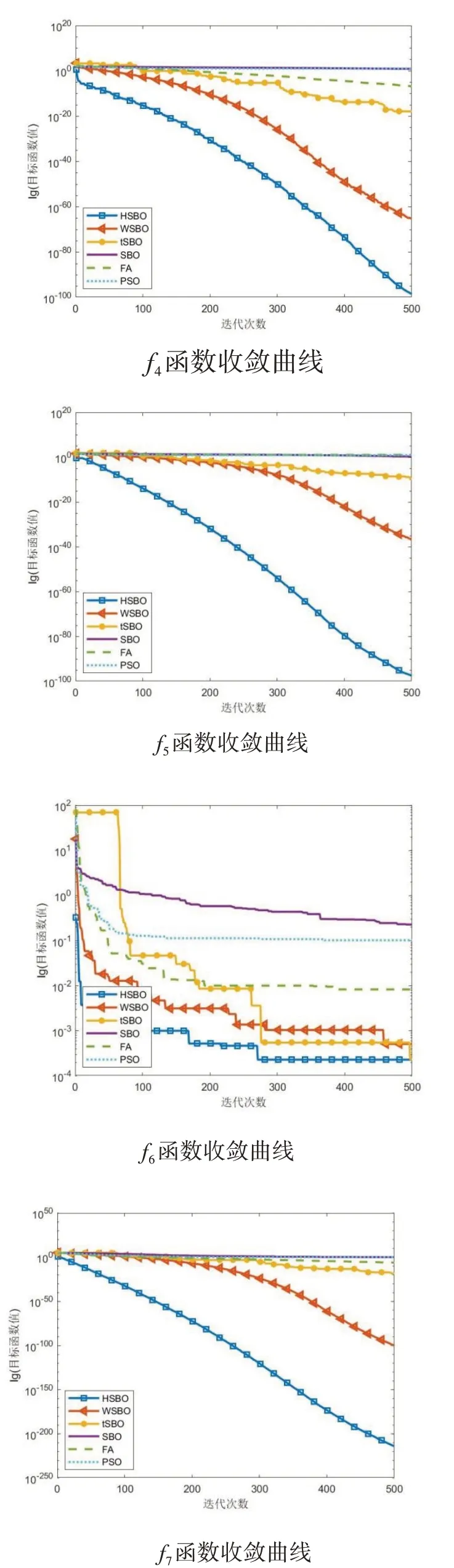
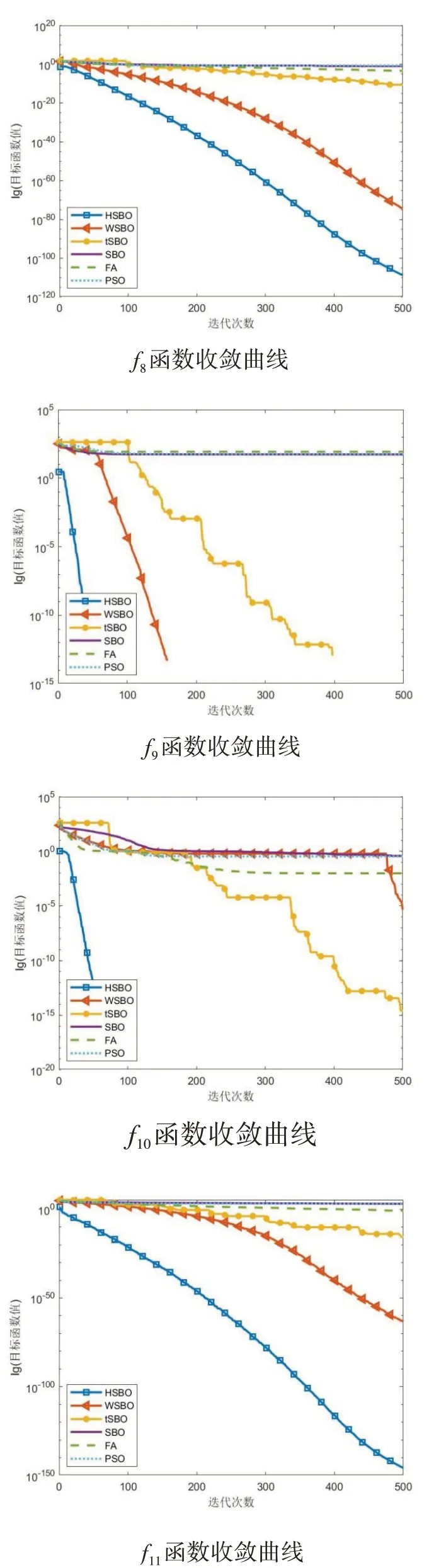
u∈(2.6,4],且u越大,混沌性越高,0 Logistic映射在分叉参数3.57 图1 Logistic映射 引入Logistic混沌映射后,提升了种群的多样性和均匀性,从而使算法能够快速收敛并接近最优解。 在原算法中,前期存在收敛速度快,容易陷入局部最优;后期收敛速度慢,搜索范围变小。因此,引入了指数惯性权重因子w,公式如下所示: 求偶亭位置更新公式: 式中,c为变化因子,it为当前迭代次数,maxIt为最大迭代次数。图2为惯性权重迭代500次的曲线图。从图中可以看出,惯性权重w总体呈递增趋势,不管是迭代初期还是迭代后期,都保持较稳定的非线性变化速度,平衡了算法的全局和局部搜索能力。这样,既继续保持了算法早期全局搜索的能力,避免陷入局部最优,又提高了算法后期的收敛速度和收敛精度。 图2 指数惯性权重曲线 标准的锻炼园丁鸟优化算法在种群变异时,使用的是高斯变异来获得新的种群,但使用此种方式的寻优速度过慢,局部搜索能力太差,容易陷入局部最优,于是引入了一种Levy飞行变异方式。 Levy飞行,是由P.Levy于1937年提出的[15],最初是用来描述生物群体的活动方式,通过对生物群体游走觅食行为的研究,逐渐形成了一种以长短距离跳跃相结合的Levy飞行。正是根据Levy飞行长短距离跳跃的多变性特点,可以使种群在迭代过程保持较高的多样性,从而在长距离搜索时能够扩大搜索范围,提高全局搜索能力,并使跳出局部最优,而更为频繁的短距离搜索,能够在更小的搜索范围内快速找到最优解。 近年来,Levy飞行已经应用于各种仿生优化算法中,并且很好地提高了算法的性能,例如基于Levy飞行策略的自适应改进鸟群算法[16],基于Levy飞行策略的改进樽海鞘群算法[17],一种基于Levy飞行的改进蝗虫优化算法[18],基于Levy飞行的萤火虫模糊聚类算法[19],等。 它的概率密度函数积分形式为: 该积分用来计算随机数分布是一个难题,后来,Xin-She Yang与Suash Deb在提出的布谷鸟算法中将Levy分布的密度函数进行了简化,得到了它的幂次形式[20]: 其中,t为步长,β为指数参数,将Levy飞行作为变异算子引入到SBO算法中: 经过实验,发现Levy飞行分布有较好的扰动性能,增加了变异的范围,提高了算法的局部搜索能力,避免了陷入局部最优。 对于SBO算法中存在的求解精度低,收敛速度慢,易陷入局部最优等问题,本文提出了一种基于混合策略改进的锻炼园丁鸟算法,在种群初始化时,加入了Logistic混沌映射,使初始种群分布更均匀;在位置更新时,引入了指数惯性权重;又在种群变异时,改变了原有的正态分布变异方式,引入了Levy飞行变异。HSBO的算法步骤如下: (1)初始化种群的大小nPop,最大迭代次数maxIt等参数,根据公式(8)来初始化种群。 (2)计算种群个体的目标函数值,确定种群中的最优位置xelite和最优值。 (3)用公式(2)计算每个求偶亭的适应度值,并通过公式(1)来算出每个求偶亭被选中的概率。 (4)用公式(4)计算步长,公式(9)计算权重因子,再用公式(10)来更新求偶亭的位置。 (5)当rand (6)将旧种群和变异种群进行组合,更新全局最优解和最优值。 (7)判断是否达到最大迭代次数,如果是,则输出最优解和最优值;否则,跳转到(3)继续迭代。 为了验证HSBO算法的性能,本文将采用12个测试函数对HSBO算法进行仿真实验,详细信息如表1所示。所要测试的算法的种群规模统一设为20,最大迭代次数为500次,维度为30,并与基于自适应权重的缎蓝园丁鸟优化算法[21](WSBO)、基于自适应t分布变异的缎蓝园丁鸟优化算法[22](tSBO)、缎蓝园丁鸟优化算法(SBO)、萤火虫算法(firefly algorithm,FA)和粒子群算法(PSO)进行实验对比。各种算法的参数设置:SBO算法、tSBO算法和WSBO算法参数:最大步长α=0.94,缩放比例因子z=0.02,变异概率p=0.05;HSBO算法参数:最大步长α=0.94,缩放比例因子z=0.02,变异概率p=0.05,混沌参数u=3.98,变化因子c=0.8;FA算 法 参 数:β0=2,α=0.2,γ=1。PSO算法参数:权重因子w=1,递减因子wdamp=0.99,学习因子c1=1.5、c2=1.5。 表1 测试函数 续表1 为了提升实验结果的可靠性,分别对每个测试函数进行30次独立实验,并算出其最优值、最差值、平均值和标准差,12个测试函数的实验结果如表2所示,通过均值可以看出算法的寻优精度,而标准差反映出算法的稳定性和鲁棒性。 表2 实验结果对比 续表2 续表2 在表2中,对于12个测试函数,本文提出的HSBO算法的实验结果在最优值、最差值和标准差上要明显优于其他算法,说明了HSBO算法具有更高的寻优精度、鲁棒性和稳定性。其中,函数f1、f2、f7、f9、f10和f12的标准方差均为0,说明改进后的算法的稳定性得到了大幅提升。在单峰测 试 函 数f1、f3、f4、f5、f6、f7、f11和f12结 果 中,HSBO算法的综合性能要高于WSBO、tSBO、SBO、FA和PSO。除了在单峰函数上有良好的表现,HSBO算法在多峰函数上也达到了较好性能。在Griewank函数f2的测试结果中,HSBO算法达到了最优的寻优精度,且标准差为0,对于Alpine函数f8,HSBO算法都获得了最好的最优值、最差值和标准差,而对于Rastigin函数f9和Griewank函数f10,最优值、最差值和标准差都为0,说明在多峰函数的测试上,HSBO算法的寻优精度和稳定性也同样明显高于其他算法。 为了进一步体现HSBO算法的性能,图3给出了上面所有算法在12个测试函数上的收敛曲线图。从图中可以看出,HSBO的初始最优值明显要优于其他5个算法,充分证明了Logistic初始化能使初始种群分布更均匀,在迭代开始时就有一个较好的初始寻优精度;函数f1、f3、f4、f5、f7、f8、f9、f10、f11、f12的收敛图近似于直线,说明算法在整个迭代过程中,收敛速度均匀,有较好的全局搜索能力,避免了陷入局部最优;从f2函数的收敛曲线可以看出,HSBO算法在未达到最大迭代次数500次时,就已经找到了最好的寻优精度,说明了算法的寻优性能高、收敛速度快;而f6函数的收敛曲线表明,HSBO算法对比于其他算法,具有更快的收敛速度、更高的寻优精度,并且在迭代中期,就已经接近或达到了最优值。 图3 测试函数收敛曲线 针对标准缎蓝园丁鸟优化算法存在的收敛速度慢、寻优精度低和易陷入局部最优等问题,本文在种群初始化时,引入了Logistic混沌映射,在位置更新时,加入了指数惯性权重,又在个体变异时,引入了Levy飞行变异,最终提出了一种基于混合策略改进的缎蓝园丁鸟优化算法HSBO。该算法改善了标准SBO算法的不足,提升了种群的全局和局部搜索能力,加快了算法的收敛速度,提高了收敛精度。本文还对算法进行了12个测试函数的仿真实验。实验结果表明,HSBO算法的收敛精度、收敛速度和寻优性能要明显优于基于自适应权重的缎蓝园丁鸟优化算法、基于自适应t分布变异的缎蓝园丁鸟优化算法、标准缎蓝园丁鸟优化算法、萤火虫算法和粒子群算法。下一步研究的工作是将改进后的算法应用到更多的领域。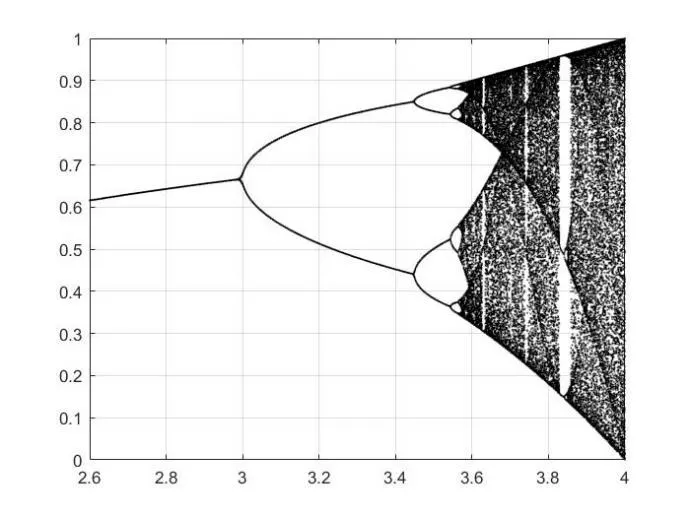
2.2 指数惯性权重
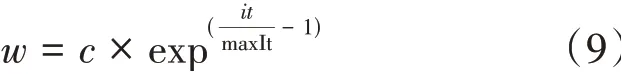
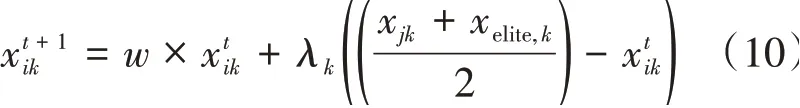

2.3 Levy飞行变异

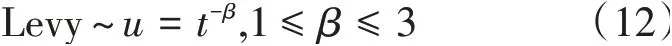
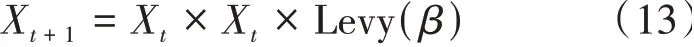
2.4 基于混合策略的缎蓝园丁鸟优化算法
3 HSBO性能测试
3.1 测试函数及参数设置


3.2 仿真实验结果分析

4 结语
