基于校园卡数据的学生行为分析的研究

2021-11-30葛昆武丁杰邹德龙向琴宋夏芝

现代计算机 2021年29期

葛昆，武丁杰，邹德龙，向琴，宋夏芝

（中国民用航空飞行学院，广汉618300）

0 引言

随着互联网的发展与成熟，“智慧校园”一词成为高校未来建设的重要一环。智慧校园需要互联网校园中心的建立，实现互联互通和解决计算存储问题。高校在实现数据存储情况已经基本完成，由各个学校的校园卡作为载体进行数据的转载。但是，各个信息作为单独的个体独立存储，距离真正的智慧校园还是有一定的差距。如何拉动各个系统之间的数据实现跨系统的联动是未来工作的重中之重。目前，以中国民用航空飞行学院的校园卡为例，学生的在校行为是处于被记录状态，学生日常在校的消费时间、消费记录都可以很好地被保存下来，学生众多的日常行为都可以通过数据反应出来。

本文基于中国民用航空飞行学院的校园卡的数据，对学生在校的日常行为进行分析。每年国家提供给家庭困难的大学生许多经济援助，但是我们常常发现由于需要判定的条件很多，以及认证环节存在的不规范现象，仅仅通过一纸认定会造成偏差。本文通过对校园数据的挖掘，整理分析基于校园卡的学生在校数据，对学生在校的消费记录进行整理和分析，从而反应个体或者群体在校的整体情况，为今后校园食堂的整改、贫困学生的认证提供有效的数据支持，为今后贫困学生的认定提供一个有效手段。

1 基于学生个人数据的画像建立

用户画像是一种工具，它可以将用户的行为数据和用户属性结合起来，根据用户的消费、习惯、社交等给用户贴上不同的标签。如图1所示是构建用户数字画像的基本流程。

图1 构建用户数字画像流程

中国民用航空飞行学院的学生卡记录了学生的校园生活消费的地点，间接记录了一个学生在校运动的轨迹，包含了餐厅消费的金额、餐厅消费的时间、洗澡时间等等，搜集这些数据抽象化构建学生的虚拟形象，学生在校的行为分析如图2所示。

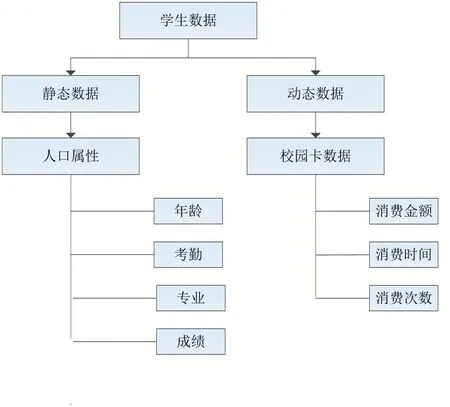
图2 学生在校行为分析

2 数据的预处理

由于学生在校流水数据众多，这些数据都存储在数据库中，本实验仅仅研究学生在校的消费情况，由于人员操作失误或者因为机器本身的影响，我们拿到的数据会存在一些错误、丢失或者内容重复等问题。为了使后续实验进展顺利，我们需要对数据进行清洗。

2.1 数据清洗

数据清洗就是将我们获得的杂乱无序、错误、重复、不符合规则的“脏数据”修正为可以直接带入模型的“干净数据”的过程。数据的预处理主要是去除缺失值，处理异常值，对文本字符串进行简单处理等。

2.2 数据集成

进行预处理之后的数据为了便于进行数据挖掘我们需要对多种不同类型的数据进行集成操作。由于在实际存储过程中会面临着由于数据类型不一致的问题、因此我们需要根据具体情况对不同数据进行集成使得最后输入的数据符合要求。

2.3 数据变换

数据变换主要是针对不同形式的数据化为统一的形式。本文主要研究学生消费情况，将变换后具有一致性的数据进行聚集、泛化等操作对数据进行离散化操作。离散化的数据具有稳定性强的特点，能够使得拟合风险减小。

2.4 数据规约

大量数据的挖掘不利于效率的提高，为此我们需要对数据进行压缩。数据的规约就是通过变换在保证数据原来样子的情况下对数据进行压缩处理，常见有维规约、数量规约以及数据压缩等方式。由于存储中的数据和本文没有直接联系，我们可以使用数据规约减少需要处理的数据量。表1、表2为校园卡消费数据进行删除数据规约的比较。

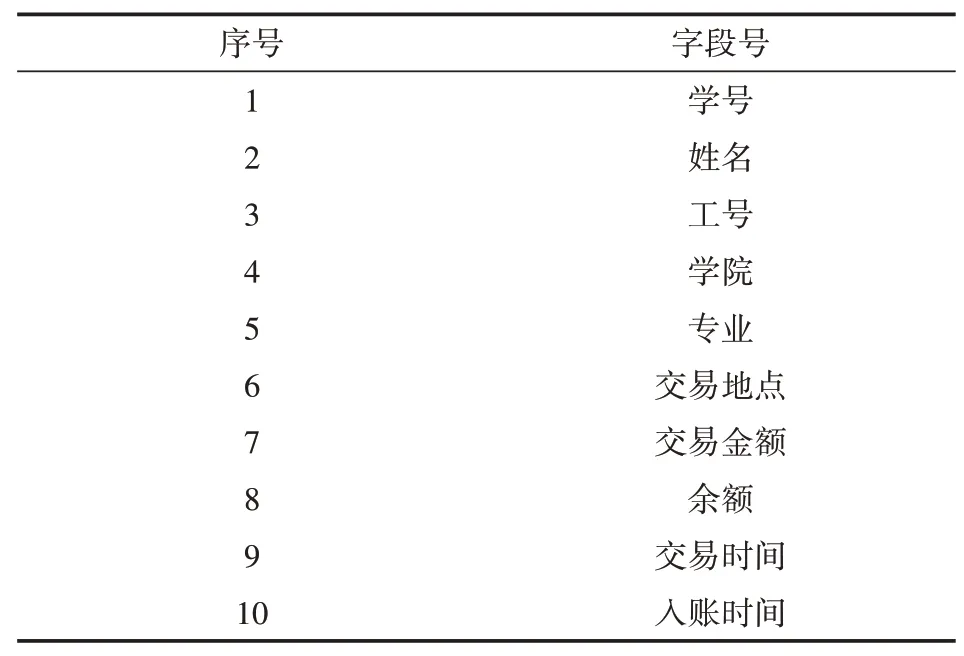
表1 原始学生校园卡消费数据

表2 数据规约后学生校园卡消费数据

3 算法介绍

3.1 K-means聚类算法介绍

K-means算法是无监督学习中一个非常典型的例子。可以用一个比较好理解的例子来解释：大学开学迎来了一大批新生，喜欢音乐的同学加入到了音乐社，喜欢动漫的同学加入到了动漫社，喜欢计算机的同学加入到了计算机社，虽然天南地北不认识的人借着这个机会相互认识形成一个个小团体，小团体在更多同学的加入下逐渐壮大，最终形成规模，也就是社团。归属感使得相似的人走到一起，不相关的人渐行渐远，就形成了物以类聚，人以群分。

机器学习中的数据样本也是如此。相似的样本归为一类，用这几个样本的中心位置表示这个类别，方便其他相似样本的加入，每当类别中有新的相似样本的加入，就更新类别的中心位置，方便新样本适应类别，这就是K-means算法的主要逻辑。

在数学上我们使用两点在欧式空间中的距离定义相似度，即两个点在欧式空间的距离。距离越近表示两个点越相似，反之两个点越不相似。为了表示相似的点属于一类，我们引入了“clus⁃ter”概念，即属于一个cluster的样本都是相似的，也就是一类。为了表述cluster准确信息，还需要定义cluster坐标位置也就是centroid评估离哪个cluster更相似，每个centroid的坐标就是所有cluster的中心也就是均值。

K-means算法思想：假设存在X1=（0，2），X2=（0，0），X3=（1.5，0），X4=（5，0），X5=（5，2），K=2，即将X1～X5这5个点集分为2类，由于X4与X5距离较近X1，X2，X3距离较近，所以将C1=（X1，X2，X3）分为一类，将C2=（X4，X5）分为另一类，算出两个分类的重心M1={（0+0+1.5）/3，（2+0+0）/3}={0.5，2/3}，M2={（5+5）/2，（2+0）/2}={5，1}。求出几个点到M1、M2的距离d（Xn，Mn），发现X1，X2，X3到M1距离近，X4、X5到M2距离近，证明分类合理。

3.2 K-means算法流程

（1）给定N个集合；

（2）将不同簇的中心初始化；

（3）计算样本到各个中心点距离，选择距离最近的为该点属于的簇；

（4）知道更新上限，重新计算中心点；

（5）直到不再变化为止。

4 结果分析

由于目前学生申请国家补助存在一纸评定的问题，各项信息停留在主观评判，材料申请的客观性难以评判，导致一些学生之间存在着虚假信息的上报，使得有限的资源不能给到需要的同学，造成资源的浪费。根据调查，学生在校消费行为主要分为三个部分，一是主要在各个食堂的刷卡消费，这是主要的：其二是利用校园卡在校园商店购买包括日常生活用品、学习工具、零食、饮料等费用，这两点是我们可以记录并保存下来的。其三是学生点外卖，由于疫情期间，学校禁止外卖入内，这部分我们可以忽略不计。在此大环境下，学生的日常活动和消费都集中在校内，也就是说，校园一卡通承载了学生在学校几乎所有的消费，可以保证我们的研究相对准确，从学生的校园卡消费可以间接反应学生的消费水平，从而看出学生的家庭经济情况。为了公平，防止有学生存在侥幸心理，我们可以将校园消费作为评判学生是否具有评选资格的重要条件，目前已知有部分高校会每个月在校园卡消费较低的同学卡中给予一定的资金援助，这种行为值得推广，并且可以优先给予这部分学生校内兼职的机会。所以，我们针对学生在校校园卡的研究，对解决实际问题具有一定的实际意义。

图3 利用K-means算法对学生在校月消费金额进行聚类分析。根据实际情况，利用K-means算法将学生的月平均消费情况分为三个层次，即高额水平消费、中等水平消费，以及低水平消费。将聚类中心个数K的值设计为3，此时得到的聚类中心为425.6，637.5，821.2，结果如图3所示。

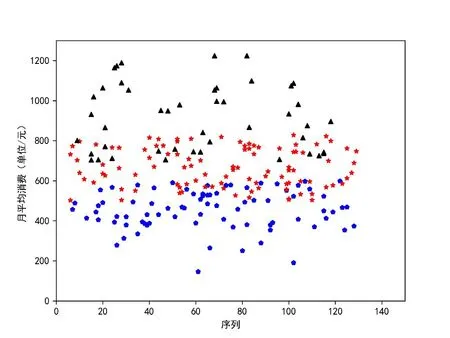
图3 月均消费聚类结果

根据K-means聚类得到的结果如图4所示。

图4 月均消费人数比例分布

根据分析可得所有的样本分为3个簇，样本分别为55%、26%和19%，分别表示有55%的学生月平均消费在637.5元左右，有26%的学生月平均消费在425.6元左右，有19%的学生月平均消费在821.2元左右。如表3所示。

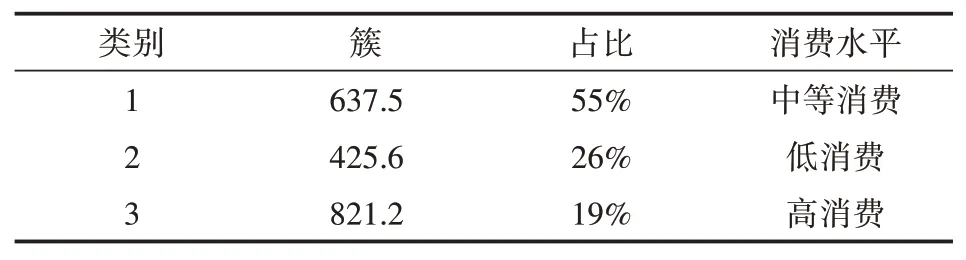
表3 聚簇结果

通过对学生校园卡消费情况进行分析，有26%左右数量的学生在校消费水平处于较低位置。针对这些学生的消费情况，学校负责相关事宜的老师可以主动去进一步了解这些学生目前的生活和学习情况，针对提交家庭困难学生申请报告且处于低水平消费一栏的学生给予勤工助学的帮助，对于申请贫困生报告但是月平均消费水平为高的学生应该再进行走访调查。在大数据的支持下，奖学金、助学金的发放将更加透明。