基于一维堆叠池化融合卷积自编码器的HRRP目标识别方法
2021-11-29张国令吴崇明
张国令, 吴崇明, 李 睿, 来 杰, 向 前
(1. 空军工程大学防空反导学院, 陕西 西安 710051; 2. 西京学院, 陕西 西安 710123)
0 引 言
雷达高分辨率距离像(high resolution range profile,HRRP)不仅能够反映目标散射点沿雷达视线方向的分布情况,而且包含目标的结构特征,为目标识别提供了重要的目标结构特征信息。且相较于二维距离像,一维HRRP更易获取、处理以及存储,因此HRRP目标识别成为雷达自动目标识别研究领域的热点[1-3]。如何提取有效特征是HRRP目标识别的关键,现已有不少相关研究[4-6]。如基于核主分量相关判别分析的特征提取法[4]、基于字典学习的鲁棒性特征提取法[5]、基于特权信息的特征提取法[6]等。由于这些方法基于浅层线性结构,所以提取的特征表达能力受限,而且特征需要人为设计,限制了识别性能的提升。因此,如何自动提取目标的深层特征成为雷达目标识别的研究热点。
深度学习本质上是利用深度神经网络自动提取目标的深层特征,目前已经在HRRP识别领域取得一些研究成果[7-10]。Pan等[7]提出了一种基于t分布随机邻域嵌入(t-distributed stochastic neighbor embedding, t-SNE)和判别深度置信网络(discriminant deep belief network,DDBN)的HRRP识别模型,该模型利用了HRRP的深层特征进行识别。杨予昊等[8]提出一种基于卷积神经网络(convolutional neural network, CNN)的HRRP识别方法,充分发掘HRRP所包含的深层属性特征,并实现了自动特征提取。Feng等[9]提出一种用于HRRP识别的堆叠校正自编码器(stacked corrective auto encoder,SCAE),实验表明该方法具有较强的特征提取能力。Zhao等[10]利用堆叠自编码器(stacked autoencoder,SAE)提取HRRP高层次特征,利用极限学习机(extreme learning machine,ELM)代替反向传播(back propagation, BP)网络,实现了对小样本HRRP数据集的快速准确识别。
作为一种深度神经网络,卷积自编码器(convolutional autoencoder,CAE)因其提取数据深层特征的能力受到了广泛关注[11-14]。Chen等[11]利用CAE通过无监督学习提取CT图像特征,成功地应用于医疗领域。Huang等[12]采用卷积核为自编码器的基本单元,提出深度CAE(deep CAE, DCAE),利用CNN的层次特征提取的优势来提取脑功能核磁共振数据中的特征,取得了较好的效果。Luo等[13]提出一种卷积稀疏自编码器(convolutional sparse autoencoder, CSAE),利用CSAE提取到的图像局部特征初始化CNN进行分类。Du等[14]提出一种堆叠卷积去噪自编码器(stacked convolutional denoising autoencoder, SCDAE),该网络以卷积方式叠加多层去噪自编码器来实现分层训练优化,每层利用去噪自编码器学习的核函数对下层的特征进行卷积,生成高维特征映射。CAE采用了自编码器的思想进行无监督特征学习,通过卷积和池化操作来提取数据的深层结构特征。
从HRRP目标识别的研究现状来看,利用CAE进行HRRP识别的研究很少,本研究旨在设计出性能良好的CAE网络,提取HRRP有效深层特征,实现目标识别。为了充分利用HRRP数据的内部结构信息,进一步提高雷达HRRP目标的识别准确率,本文提出了一种一维池化融合CAE(one-dimensional pooling fusion CAE, 1D PF-CAE)。在编码阶段,利用最大池化和平均池化提取特征并融合,两者提取到的特征互相补充丰富,然后将1D PF-CAE堆叠形成一维堆叠池化融合CAE(one-dimension stacked pooling fusion CAE, 1D SPF-CAE),从而增强其深层特征提取能力,进一步提出了基于1D SPF-CAE的HRRP目标识别方法。同时,考虑到深层网络固有的训练困难问题,使用Ada-Bound[15]优化算法优化网络训练,以提高网络的整体性能。实验结果表明,本文提出的基于1D SPF-CAE的HRRP目标识别方法取得了良好的效果。
1 CAE原理
1.1 CAE
自动编码器由两部分组成:编码器和解码器,如图1所示。
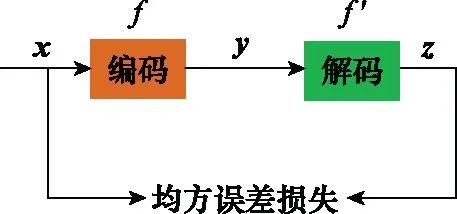
图1 自编码器架构Fig.1 Architecture of autoencoder
编码器使用确定性的映射函数将输入x映射到隐层表示y,通常映射函数f是非线性的,y可表示为
y=f(Wx+b)
(1)
式中:W表示输入和隐层表示之间的权重;b表示偏置。
解码器通过隐层表示y重构输出z,公式为
z=f′(W′y+b′)
(2)
式中:W′是隐层表示与输出之间的权重;b′是偏置。
(3)
CAE将卷积连接和自编码器结合在一起,由卷积编码器和卷积解码器组成[16]。卷积编码器实现输入到特征的卷积转换,卷积解码器实现特征到输出的卷积转换。在CAE中,通过CNN计算提取的特征和重构输出。因此,式(1)和式(2)可改写为
y=ReLU(wx+b)
(4)
z=ReLU(w′y+b′)
(5)
式中:w为x和y之间的卷积核;w′为y和z之间的卷积核。
一维堆叠卷积自编码器(one-dimensional stacked CAE,1D -SCAE)是一种特殊的卷积自编码器,其原理如下节所述。
1.2 1D -SCAE
1D -SCAE由多个一维CAE(one-dimension CAE, 1D -CAE)分层堆叠而成,前一个1D -CAE编码器的输出为后一个1D -CAE的输入[17]。1D -SCAE能够学习到鲁棒性强、抽象度高的特征,主要有两大原因:一是与单层自动编码器相比,1D -SCAE堆叠起来的深层网络结构具有更强的特征表征能力[17];二是与全连接网络相比,1D -SCAE网络采用卷积和池化操作,能够在提取局部特征的同时,从全局上把握整体的变化特征,使得提取到的特征更具鲁棒性[18]。图2是由两个1D -CAE堆叠而成的1D -SCAE。
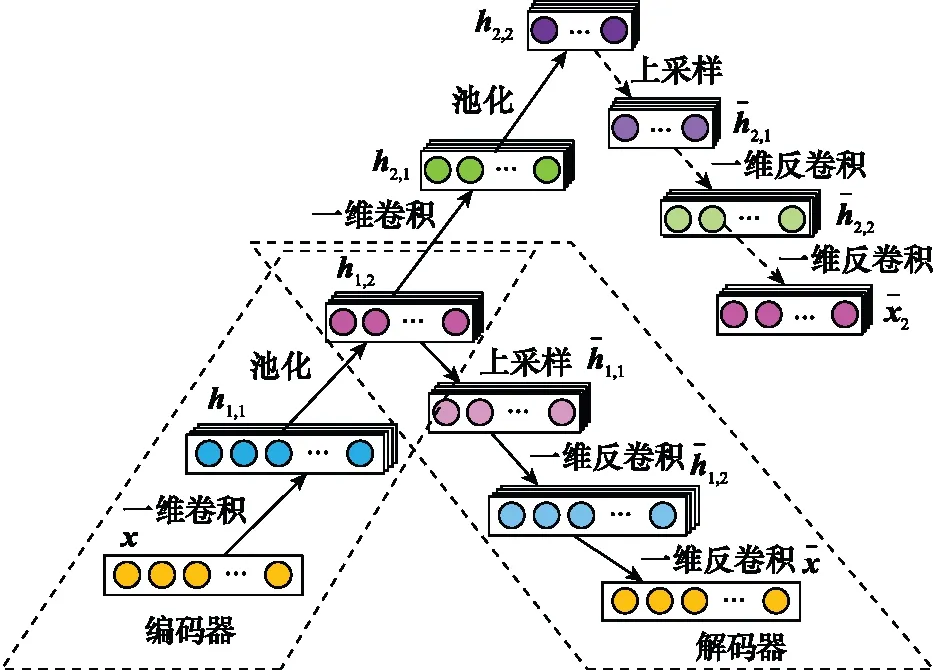
图2 1D -SCAEFig.2 1D -SCAE
每层1D -CAE在编码阶段通过一维卷积和池化提取数据的特征,在解码阶段通过上采样和一维反卷积运算重建输入。
(1) 编码过程由一维卷积和池化组成。其公式为
hi,1=ReLU(ωi*xi+bi)
(6)
hi,2=pool(hi,1)
(7)
式中:xi=hi-1(i=1,2,…,n),i=1时,xi=x;hi,1为第i个编码器的一维卷积输出;hi,2为第i个编码器输出的特征;ωi和bi分别为第i个编码器的卷积核和偏置;*表示卷积操作;pool表示池化操作。
(2) 解码过程由上采样和一维反卷积组成。其公式为
(8)
(9)
(10)
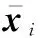
各层1D -CAE通过最小化重构误差进行训练,第i个1D -CAE的损失函数为
(11)
为进一步提高1D -CAE的特征提取能力,在上述经典1D -CAE的基础上,本文在1D -CAE编码阶段采用最大池化和平均池化同时提取特征,并将提取到的特征进行融合,设计了一种1D PF-CAE,进一步将堆叠的1D PF-CAE用于HRRP特征的自动提取,从而提出一种基于1D SPF-CAE的HRRP识别方法。
2 基于1D SPF-CAE的HRRP识别方法
2.1 1D SPF-CAE
传统的1D -CAE因其网络模型采用了CNN,具有局部连接、参数共享、池化、多卷积核等优势;而且经过池化操作得到的特征对于小范围内的旋转和平移具有较好的鲁棒性,因此具有较强的特征表达能力[19]。为进一步提高网络的表达能力,本文设计了一种1D PF-CAE,在编码阶段,同时采用最大池化和平均池化提取不同的编码特征,并将两者提取到的特征进行串联连接为最终的池化输出。在此基础上,将1D PF-CAE形成1D SPF-CAE,其网络结构如图3所示。
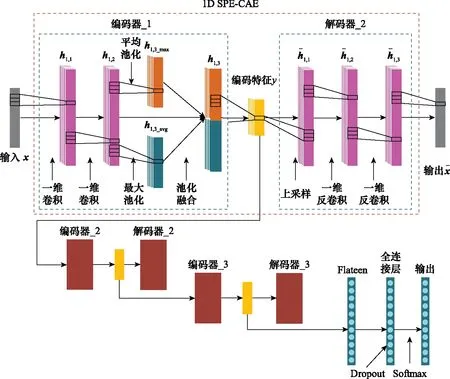
图3 1D SPF-CAE的网络结构Fig.3 Network structure of 1D SPF-CAE
其中,堆叠的三层1D PF-CAE主要用于特征提取,后面的网络主要用于分类。
1D SPF-CAE的每层1D PF-CAE都通过无监督学习来提取特征,其无监督学习分为卷积编码和卷积解码两个阶段。编码阶段,首先进行两次一维卷积操作,目的在于充分提取数据的局部结构特征;然后同时进行最大池化和平均池化操作,并将两部分不同特征进行融合作为池化输出。编码的具体过程如下所示:
hi,1=ReLU(ωi,1*xi+bi,1)
(12)
hi,2=ReLU(ωi,2*hi,1+bi,2)
(13)
hi,3_max=maxpool(hi,2)
(14)
hi,3_avg=avgpool(hi,2)
(15)
hi,3=hi,3_max⊕hi,3_avg
(16)
式中:xi=hi-1(i=1,2,3),i=1时,xi=x;hi,1为第i个编码器的第1个一维卷积输出;hi,2为第i个编码器的第2个一维卷积输出;hi,3_max为第i个编码器的最大池化输出;hi,3_avg为第i个编码器的平均池化输出;hi,3为第i个编码器输出的特征;maxpool表示最大池化操作,avgpool表示平均池化操作;⊕代表串联连接。
解码的过程与第1.2节中的解码过程等同,即式(8)~式(10)。
网络含有大量可训练的参数θ,容易导致过拟合,因此在全连接层加入Dropout技术[20],以概率随机舍弃部分节点,减少了冗余特征,缓解了过拟合现象。
2.2 训练优化
1D PF-CAE网络的训练采用小批量训练模式。随机梯度下降(stochastic gradient descent, SGD)法分批次随机抽取m个训练样本作为输入,第t次迭代时,参数更新为
θt+1=θt-αgt
(17)
式中:gt为损失函数的梯度;α为学习率。
SGD使用固定的学习率进行参数更新,存在学习率选择困难的问题,因此1D PF-CAE采用AdaBound算法对参数更新过程进行优化。每次参数更新时,AdaBound利用梯度一阶矩和二阶矩估计分别更新gt和α,同时施加动态边界限制了α的变化范围,使得参数更新过程更平稳。基于AdaBound的1D PF-CAE训练优化算法见算法1。

算法 1 基于AdaBound的1D PF-CAE训练优化算法输入: 训练集、测试集输出: 最优模型1参数配置:设置epochs为100,batchsize为200,学习率α0=0.001,αf=0.1,β1=0.9,β2=0.999,以及小常数γ=10-3,ε=10-7。2模型初始化:设置模型参数θ为近似0的随机值。3参数更新。4初始化梯度一阶矩估计:m0←05初始化梯度二阶矩估计:v0←06for t=1 to T do7根据式(11)计算前向传播误差:L(θt-1)8计算损失函数的梯度:gt←Δθt-1L(θt-1)9更新α:αt←α01-βt21-βt110计算α的下界:αl←αf(1-1γt+1)11计算α的上界:αμ←αf(1+1γt)12更新梯度一阶矩估计:mt←βtmt-1+(1-β1)gt13更新梯度二阶矩估计:vt←β2vt-1+(1-β2)g2t14更新θ:θt←θt-1-mt·min{max{αtvt+ε,αl},αμ}15end for
训练好每个1D PF-CAE之后将其堆叠构造1D SPF-CAE,然后再使用AdaBound算法对整个网络进行微调,最终采用Softmax分类器实现分类。
2.3 基于1D SPF-CAE的HRRP目标识别方法
本节利用提出的1D SPF-CAE对雷达HRRP目标进行识别,凭借1D PF-CAE提取特征能力强的优势,提取HRRP的深层结构特征;然后堆叠多个1D PF-CAE形成1D SPF-CAE;最后使用标签数据对网络进行微调,实现HRRP目标识别。
基于1D SPF-CAE的HRRP目标识别方法主要包括3个阶段:预处理阶段、训练阶段和测试阶段。
(1) 预处理阶段:对原始的HRRP数据进行去噪处理和归一化处理。
(2) 训练阶段:训练阶段分为预训练和微调。首先对3个1D PF-CAE单独训练,然后将训练好的3个1D PF-CAE按照图3进行堆叠,再对Softmax预训练。在微调阶段,对整个网络进行微调,优化1D SPF-CAE中的每个1D PF-CAE和Softmax分类器的参数,得到最终的训练模型。
(3) 测试阶段:利用训练好的网络对测试集HRRP数据进行分类得到目标类型。
3 实验与结果分析
3.1 实验设置
为了测试本文提出方法的性能,在此设计了以下实验。
实验 1模型的训练实验。
实验 2不同池化方式对方法性能的影响分析。
实验 3特征可视化分析实验。
实验 4参数影响分析实验,分析了不同堆叠层数、不同优化算法以及不同Dropout取值对方法性能的影响。
实验 5与其他算法在加噪和未加噪数据集上的性能对比分析。
3.1.1 实验环境及实验数据
本文试验环境为Tensorflow,计算机配置为Intel(R) Core(TM) i7-4790 CPU 3.60 GHz,16 GB RAM。
本文使用FEKO和Matlab联合仿真得到5类弹道中段目标的HRRP仿真数据。其中,雷达参数设置如下:中心频率10 GHz、带宽1 GHz、方位角范围0°~180°、方位角间隔0.05°。5类仿真目标及其物理参数如图4所示。

图4 5类弹道中段目标Fig.4 Five types of the target in the middle part of the trajectory
仿真得到18 005个256维的一维HRRP样本数据,每类目标HRRP数量为3 601。按照66%、33%的比例随机划分训练集和测试集,构造数据集A;按照50%、50%的比例随机划分训练集和测试集,构造数据集B;按照33%、66%的比例随机划分训练集和测试集,得到数据集C。在不加说明的情况下,以下均将数据集A作为实验数据集。
3.1.2 模型参数设置
1D SPF-CAE训练参数设置如下:学习率为0.001,批量大小为200,Dropout率为0.2。网络结构设置如表1所示。
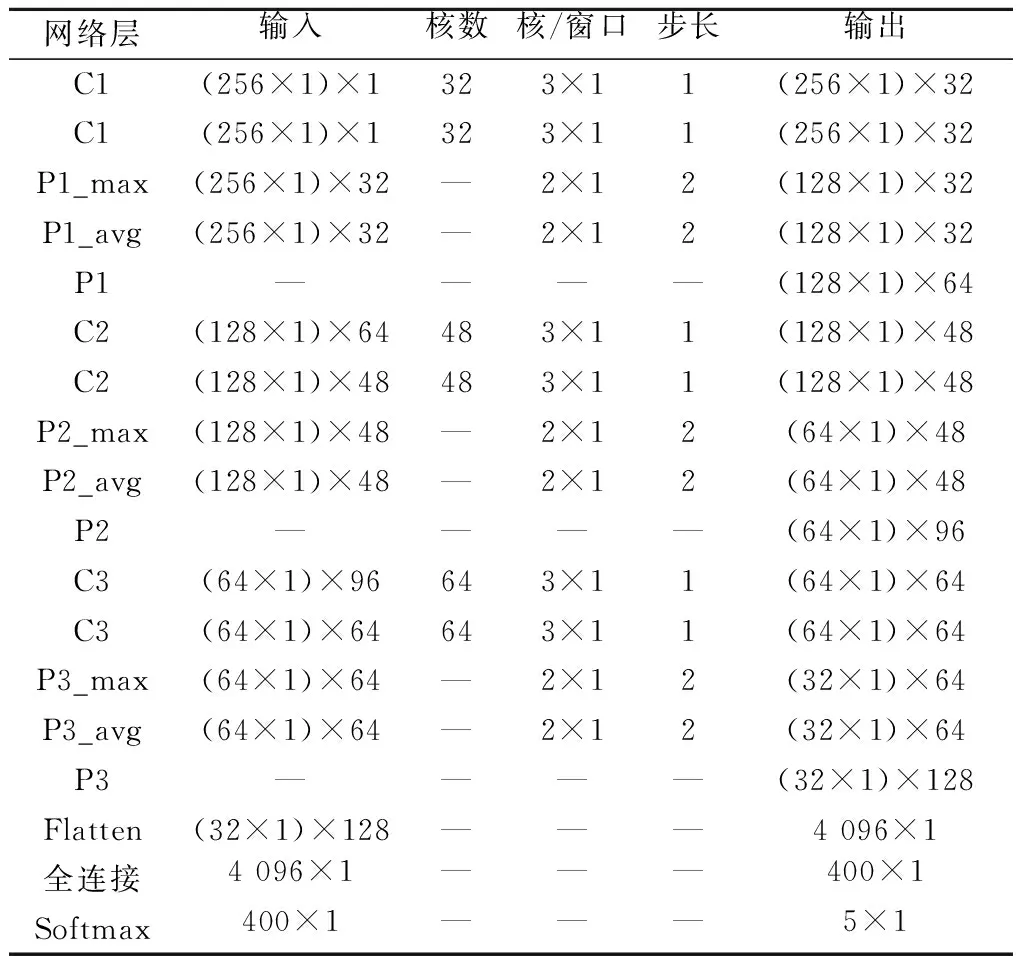
表1 网络参数设置
3.2 模型训练
在预训练阶段,1D SPF-CAE中的每一层1D PF-CAE进行无监督式学习,通过对输入数据重构提取数据的特征。在微调阶段,将各层1D PF-CAE和Softmax分类器看作一个整体去调整自由参数,参数调优的过程直观表现为损失不断降低,当损失收敛时得到的参数是最优的。实验进行100次迭代,训练集和测试集的损失变化如图5所示。

图5 损失变化Fig.5 Loss variation
由图5看出,在训练初期,损失随着迭代次数的增加而快速下降,训练后期趋于稳定且训练误差较低。说明1D SPF-CAE网络具有良好的训练效果,收敛速度快,并且收敛后训练误差小。
基于1D SPF-CAE的HRRP目标识别的混淆矩阵如图6所示。由图6可以看出,1D SPF-CAE对5类HRRP目标均具有较好的识别效果,能够很好地识别弹头和假目标。

图6 1D -SCAE的识别混淆矩阵Fig.6 Recognition confusion matrix of 1D -SCAE
3.3 不同池化方式的影响分析
为了验证本文提出的池化融合方法的有效性,本节设置对比试验:1D SPF-CAE分别采用平均池化、最大池化、平均池化+最大池化3种不同的方案,3种方案情况下的HRRP识别准确率如表2所示。通过表2看出,与其他两种池化方案相比,同时采用平均池化和最大池化的方案取得了较高的识别准确率。原因在于,最大池化能够提取到带有局部结构意义的特征,而平均池化提取到的特征包含一定的全局意义,两者提取到的特征是有区别的,通过池化融合将两者提取的特征相结合,互为补充,能够更好地反映HRRP数据的本质,因此取得了更高的识别准确率。本实验证明了本文对一维堆叠卷积自编码器的改进是有效的。
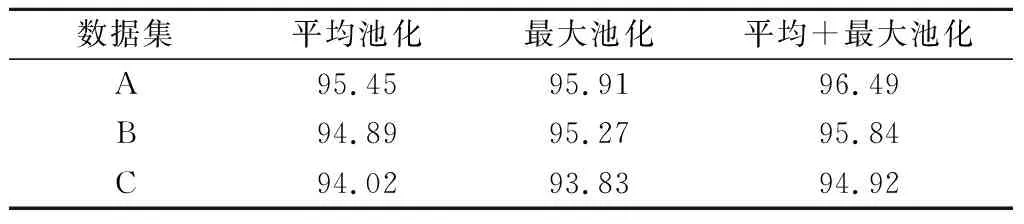
表2 不同池化方式下的识别准确率
3.4 特征可视化分析
为了验证1D SPF-CAE的逐层特征能力,用t-SNE[7]算法将输入数据、第1层1D PF-CAE输出特征、第2层1D PF-CAE输出特征、全连接层输出特征可视化到二维空间,结果如图7所示。图7(a)是对输入数据可视化,可以看出5类样本混合在一块(球形诱饵除外),图7(d)是对全连接层输出特征可视化,5类弹道中段目标呈现出很好的分类效果。而且随着网络层数加深,同类别的特征数据越来越具有相似性,不同类别的特征数据呈现出的可辨识分离性更加明显。说明1D SPF-CAE具有较强的逐层特征提取能力,而且随着网络层数增加,提取到的特征更抽象、更具有代表性。
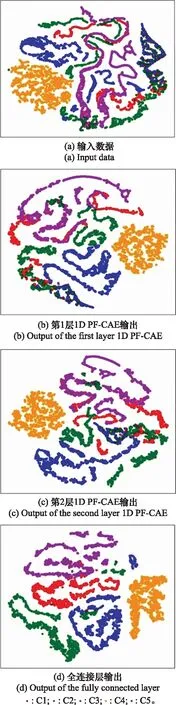
图7 t-SNE降维可视化Fig.7 t-SNE reduced-dimension visualization
3.5 参数影响分析
3.5.1 堆叠层数影响分析
为了分析不同堆叠层数对网络性能的影响,本节分别将堆叠层数设为1~6层,不同堆叠层数对应的识别准确率如表3所示。

表3 不同堆叠层数下的识别准确率
从表3中可以看出,堆叠层数从1层增加到4层时,HRRP识别准确率不断增长,说明随着堆叠层数增加,网络对HRRP数据进行多级抽象表达和有效特征提取,使得深层学到的特征更具有本质代表性,提高了识别性能。4层的网络识别准确率达到最高。堆叠层数再增加时,识别率不再增长反而下降。原因在于随着堆叠层数增加,产生了过拟合。可以得出结论:适当的增加网络深度可以增强特征提取性能,提高HRRP识别准确率。综合识别准确率和网络训练难度考虑,本文1D SPF-CAE由3层1D PF-CAE堆叠而成。
3.5.2 优化算法影响分析
为了验证本文选用的AdaBound算法对网络训练具有较好的优化作用,将其与SGD、Adadelta、Adam优化算法进行对比实验,选用不同优化算法时,测试集上识别准确率变化如图8所示。
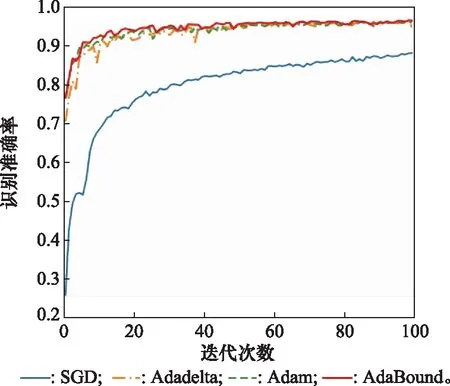
图8 不同优化算法下1D -SCAE的训练效果Fig.8 Training effect of 1D -SCAE under different optimization algorithms
由图8可得,相比于Adadelta算法、Adam算法,选用AdaBound算法对1D SPF-CAE进行训练具有更快的收敛速度;与SGD算法相比,选用AdaBound算法对1D SPF-CAE进行训练具有更高的识别准确率。实验结果表明,选用AdaBound算法对网络训练进行优化具有一定的促进作用。
3.5.3 Dropout影响分析
Dropout是解决过拟合问题的常用方法,本实验比较了1D SPF-CAE在不同Dropout率下的识别准确率,如图9所示。
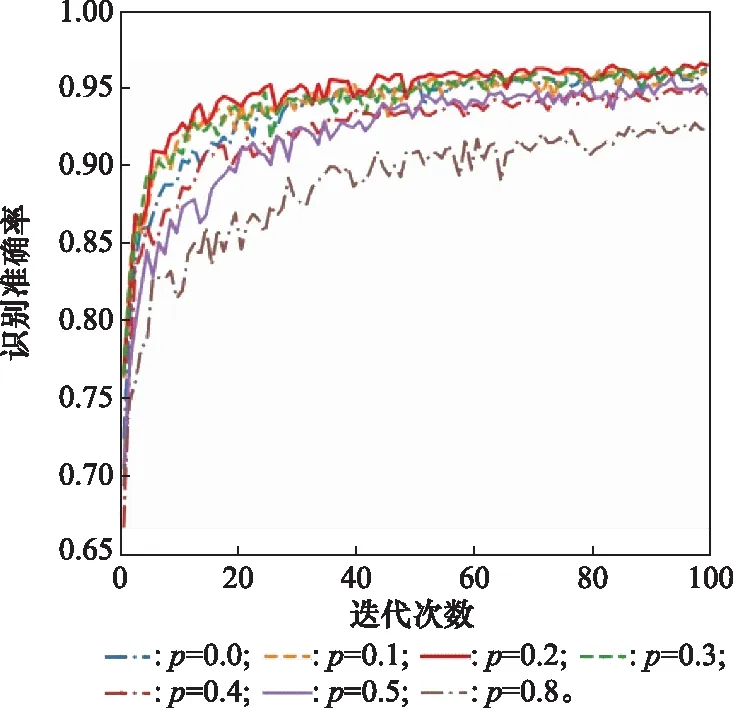
图9 Dropout率对模型的影响Fig.9 Impact of Dropout rate on the model
从图9看出,随着Dropout率的增加,1D SPF-CAE的识别性能先上升后下降,并且在p=0.2时性能达到最优,表明适当的剔除网络参数能够缓解过拟合问题,提升网络性能;而过多的剔除网络参数反而会降低算法性能。
3.6 不同算法性能对比
为了验证基于1D SPF-CAE算法的HRRP目标识别方法的综合性能,将1D SPF-CAE与多种算法进行性能对比实验。在A、B、C这3个数据集上分别添加5 dB、10 dB、15 dB、20 dB噪声,共得到15个数据集。
对比算法网络设置如下:SAE[21]、堆叠去噪自编码器(stacked denoising autoencoders,SDAE)[22]、堆叠稀疏自编码器(stacked sparse autoencoders, SPAE)[23]、基于栈式降噪稀疏自编码器的极限学习机(stacked denoising SAE based ELM,SDSAE-ELM)[24]均设置3层隐含层,网络结构均设置为256-512-356-128-5;1D -CNN包含3层卷积层、3层池化层交叉连接,最后连一个全连接层,所有池化层的窗口大小和步长均设置为2;卷积核大小为3×1,卷积核数分别为32、48、64,全连接层含有400个节点。ELM隐含层节点数设为2 000;RF的最大深度设置为50,包含600棵树。不同算法的识别准确率结果如图10所示。实验结果为10次重复试验取平均值。
观察图10,基于1D SPF-CAE的HRRP识别准确率明普遍高于SAE、SDAE、SPAE、SDSAE-ELM,原因在于1D SPF-CAE采用了卷积神经网络提取特征,相比全连接网络,CNN提取到的特征更抽象、更能反映数据本质,对于一维HRRP数据表达能力更强,提高了HRRP目标识别准确率。且1D SPF-CAE的识别准确率明显高于RF、ELM浅层机器学习算法,表明1D SPF-CAE作为深度学习算法,能够提取HRRP数据的内部结构特征,故而能够较大地提高HRRP目标识别准确率。相比于1D -CNN,1D SPF-CAE其采用自编码器的思想,首先对网络进行预训练,取得了更好的识别准确率。对比添加噪声和未添加噪声的情况,在添加噪声的数据集上,1D SPF-CAE的识别准确率提升更为明显,说明1D SPF-CAE算法具有较好的鲁棒性。
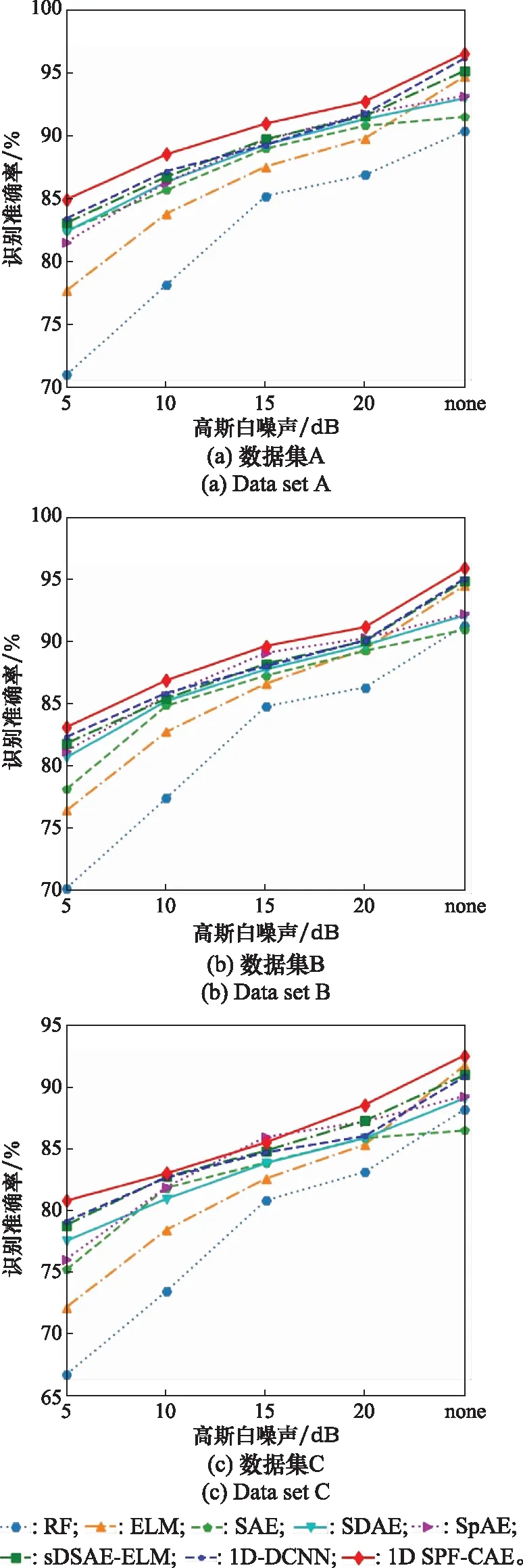
图10 不同算法在测试集上的识别准确率Fig.10 Recognition accuracy rate of different algorithms on test set
4 结 论
为了能够自动提取到HRRP自身的结构特征,本文提出了一种基于1D SPE-CAE的HRRP目标识别方法。该方法采用1D SPF-CAE自动提取目标HRRP的结构特征,使用Softmax分类器对学习到的特征进行分类。1D SPF-CAE由1D PF-CAE堆叠构成,在1D PF-CAE的编码阶段采用最大池化和平均池化同时提取不同性质的特征,并通过池化融合增强了池化层输出特征的丰富性,实验表明本文提出的方法是有效的。1D SPF-CAE通过堆叠进行多层次特征提取,有效地提高了网络提取特征的能力;同时,采用AdaBound算法优化网络增强了网络的整体性能。最终实验表明,本文提出的识别方法具有较高的识别准确率和较强的鲁棒性。
