贫信息背景下基于矩域灰点排序的灰FMECA模型

李志远, 刘思峰, 方志耕, 夏悦馨

(南京航空航天大学经济与管理学院, 江苏 南京 210016)

0 引 言

故障模式、影响和危害性分析(failure mode, effects and criticality analysis,FMECA)是一种预防性的可靠性分析技术,被广泛应用于航空航天[1-2]、汽车[3-4]、船舶[5]等领域。其以系统中所有的潜在故障模式为基础,分析每个故障模式所对应的影响、发生可能性,并确定其危害性。依据危害性大小排序,可以找出系统中的薄弱环节,进而有针对性地实施补救。FMECA包括故障模式及影响分析(failure mode and effects analysis, FMEA)和危害性分析(criticality analysis, CA)两个部分[6]。常用的CA方法有风险优先数法(risk priority number, RPN)和危害性矩阵法两种。RPN法主要应用于汽车工业领域,其危害度计算方法即发生度(O)、严重度(S)及不可探测度(D)3项指标相乘[7]。危害性矩阵法常用于航天工业中,是通过绘制危害性矩阵图来进行定量CA或定性CA。

总结上述文献,目前关于改进FMECA方面的研究,主要是以解决语义模糊性和寻求多属性科学决策的角度为出发点,而对于贫信息背景下相关的FMECA研究尚未出现。事实上,由于试验样本费用高、研制方案筛选难度大等因素,贫信息问题在复杂装备可靠性领域是常见的[23]。贫信息背景具备两大特点:数据量少、信息不准确[24-25],在工程中具体代表产品有运载火箭、航母和飞机等。FMECA作为主要应用于设计阶段的可靠性分析方法,特别是当一个全新的复杂产品在初次设计时,很难有类似的历史信息作为参考。专家在此类情景下,往往难以对故障信息做出客观判断。而目前学者利用模糊语言进行的语义处理,是建立在专家已有客观判断的基础上进行的,并不能解决数据源信息缺失的难题。因此,针对贫信息背景下的FMECA研究具有重要的理论意义和现实意义。

考虑到贫信息背景对定量危害性矩阵法影响较大,本文重点关注定量危害性矩阵图法的FMECA改进研究。为改进传统危害性矩阵图的缺陷,设计新的规范化危害性矩阵图进行CA分析;针对贫信息背景特点,在危害度计算中引入区间灰数,并提出矩域灰点概念,分析矩域灰点的一般排序规则,以此建立适用于贫信息背景下的灰FMECA模型。

1 危害性矩阵图规范化改进设计

应用FMECA的流程一般包括系统定义、故障模式分析、故障原因分析、故障影响及严酷度分析、故障检测方法分析、改进措施设计分析、CA和生成FMECA报告等8大步骤,前6步也属于FMEA内容。由于不涉及计算,贫信息对FMEA影响不大,因此前6步基本不变。本节首先探讨CA中危害性矩阵图存在的问题及改进策略,后续探讨基于改进的危害性矩阵图故障模式危害性的灰色表征及排序方法。

在传统定量危害性矩阵图中,对故障模式所处点往危害性矩阵图45°斜对角线引垂线,通过比较垂足至原点的距离来确定故障模式或产品的改进优先次序。有文献指出其存在下列问题[19]:① 横坐标严酷度级别没有量化,不能精确标识。② 横纵两轴指标数值意义不同,手工作图对危害度排序存在误差影响。

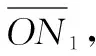
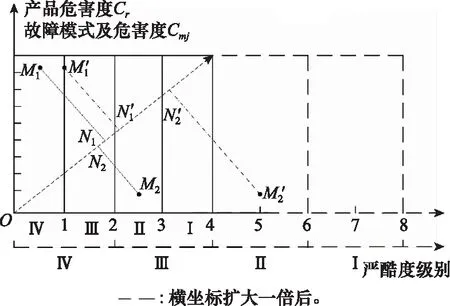
图1 定量危害性矩阵作图误差示意图Fig.1 Schematic diagram of mapping error of quantitative criticality matrix

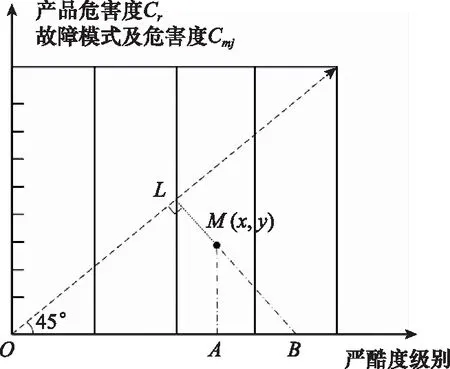
图2 定量危害性矩阵解析图Fig.2 Graphical analysis of quantitative criticality matrix

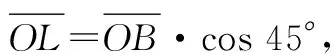
(1)

由此可见,定量危害性矩阵法得到的危害度实际上正比于故障模式点M(x,y)横纵坐标的简单加和。此处加和是图纸上长度的加和,在实际绘制中受绘图比例影响较大,极易造成偏差。其次,定量危害性矩阵法的实质是按绘图比例将严酷度级别和危害度求和,两者单位并不相同,这样求和严格而言不符合量纲法则。

本文提出一种规范化的定量危害性矩阵图。首先处理量纲不一致问题,通过将序列中每个危害度数值与序列最大危害度数值相除,消去量纲。对量化后的横坐标严酷度级别进行同样的处理,控制最严重的严酷度级别的量化值始终是1。此时定量危害性矩阵图的横纵轴上均是介于0和1之间的无量纲数据。

定理 1在定量危害性矩阵图中,将序列中每个危害度数值与序列最大危害度数值相除,不会改变故障模式危害度之间的大小排序顺序。

证明设有故障模式危害度序列{Cm1,Cm2,…,Cmn},将其从小到大进行排序得{Cmin,Cmi,Cmj，…,Cmax}。将序列中每个危害度数值与序列最大危害度数值相除后得新序列{Cmin/Cmax,Cmi/Cmax,Cmj/Cmax，…,1},仍满足Cmin/Cmax≤Cmi/Cmax≤Cmj/Cmax≤…≤1,顺序不变。

证毕

其次解决受绘图比例影响问题,考虑到定量危害性矩阵法的实质是按绘图比例将严酷度级别和危害度求和,因此可设置求和的权重系数,依据权重系数确定绘图比例。

定义 1在某一产品的FMECA分析中,称消除量纲后的危害度相对于严酷度的重要性比为危害度权重比kw。

危害度权重比kw体现了该产品FMECA分析人员对危害度指标的重视程度,kw越大,表示越重视危害度指标,即越重视故障频数比α、故障影响概率β等危害发生概率性的指标;反之kw越小,表示越重视严酷度指标,即更加看重故障发生所造成的后果有多严重。对于不同类型产品、不同结构的系统,应选用适合的危害度权重比kw。因此规范化后的定量危害性矩阵图如图3所示,选取基础作图比例为横轴∶纵轴=1∶1,即两者均取一个绘图长度单位1U,再依据实际情况将纵轴扩张kw倍,即纵轴取kw个绘图长度单位kwU。每个故障模式的坐标均可依据所处位置得到,表示为M(x,y)=(xU,ykwU),其中0≤x,y≤1。

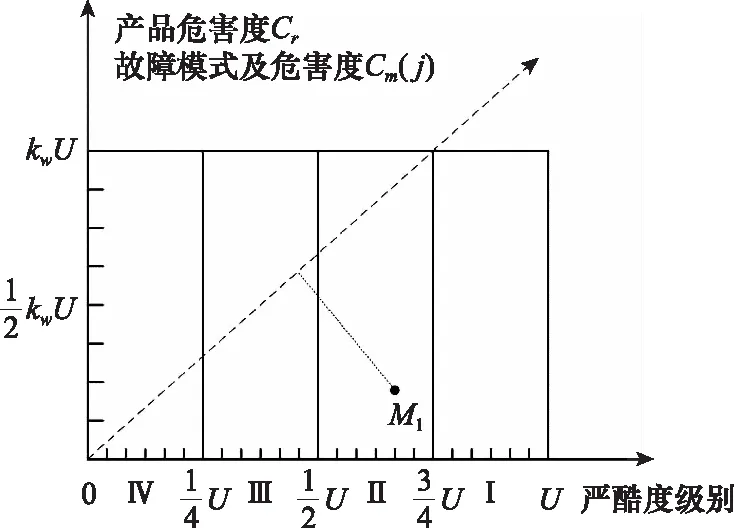
图3 规范化的定量危害性矩阵Fig.3 Standardized quantitative criticality matrix

2 贫信息背景下灰FMECA模型

2.1 基于区间灰数的危害度计算

CA需计算每个故障模式的危害度和产品的危害度,并对故障模式和产品分别进行危害度排序,以找出系统薄弱点。贫信息背景下故障信息少,应充分利用历史故障信息来帮助完成FMECA工作。参照文献[26]方法按系统层次提取相同或相似历史故障模式信息,包括故障模式影响概率、故障模式频数比和失效率。由于贫信息系统内外扰动因素的存在和小样本本身的偶然性局限,这些历史故障信息不能完全代表当前的故障模式,因此由专家参考历史故障信息,估算出故障参数的大致取值范围。对危害度计算引入区间灰数,以表达故障参数只知大致范围而不知确切取值的情形。

如在第j个故障模式的分析中缺乏故障模式影响概率数据βj,经参考同类历史故障模式后,由专家确定βj的大致范围在a～b之间,则记作:灰数βj(⊗)∈[a,b]。其余同理,故第j个故障模式的危害度计算如下:

Cmj(⊗)=αj(⊗)βj(⊗)λp(⊗)t

(2)

式中:j=1,2,…,n,n为产品所有的故障模式总数;αj(⊗)为产品第j种故障模式的频数比;βj(⊗)为第j种故障模式发生导致既定严酷度级别的条件概率,一般由工程经验获得[27];λp(⊗)为产品在任务时间内的失效率;t为产品的任务时间。

产品危害计算如下:

(3)

使用区间灰数表征故障参数时,求得的危害度是由故障模式频数比、失效率等一系列区间灰数组成的映射关系集合,为了求得危害度的最终范围,可根据文献[28]提出的灰数全局优化算法求解危害度的最值,求解规划模型为

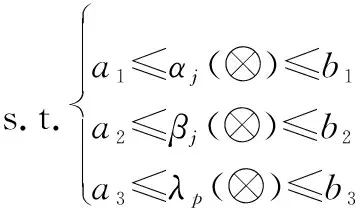
(4)

定理 2式(4)中规划模型的解在各区间灰数端点处取得,对应的解为

minCmj=Cmj(a1,a2,a3)
maxCmj=Cmj(b1,b2,b3)

证明依次将αj,βj,λp看作有取值范围的变量求偏导,由于三者不相关,所以

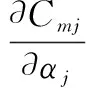
即目标函数关于三者均递增,于是当区间灰数为端点值时,式(4)中规划模型获得最优解。

证毕

2.2 基于矩域灰点排序规则的故障改进次序

前面给出了贫信息背景下的危害度计算方法,绘制规范化的定量危害性矩阵图可进一步得到每个故障模式或产品所处的位置,本节需要按位置对故障模式或产品进行排序,以确定相应的改进优先次序。

贫信息情形的危害度数值不是确切的数,同样严酷度级别也可能难以知其确切值,两者均用区间灰数表示。于是在绘制的危害性矩阵图中,故障模式不再是以一个点呈现,而是矩形区域内的一个未知点,该矩形代表了故障模式点所有可能处在的位置。为了探究此类情况的CA,提出“矩域灰点”的定义。

定义 2设平面直角坐标系内存在一个具体位置不确定的点,其横坐标和纵坐标分别介于区间[a,b]和区间[c,d]之间,且两者取值独立,则称其为矩域{(x,y)|a≤x≤b,c≤y≤d}内的矩域灰点,记作Θ∈([a,b],[c,d])。进一步,对应的横坐标用区间灰数⊗1∈[a,b]表示,纵坐标用区间灰数⊗2∈[c,d]表示,则矩域灰点Θ简记为Θ∈(⊗1,⊗2)。

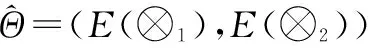
矩域灰点的本质仍是一个点,其横纵坐标可能的上下界限确定,且横纵坐标取值相互独立,是用以表达只知可能所处的矩形区域而不知其确切位置的点。

2.2.1 有相同历史故障信息情形的排序

当存在相同历史故障信息,取相同历史故障参数的平均值作为矩域灰点的实核点。此类情况故障模式在危害性矩阵图中以已知实核点的矩域灰点呈现。在该矩域内,故障模式最可能处在实核点的附近,但也可能处在矩域内其他任意位置,这是典型的不确定条件下的排序问题。而FMECA分析进行危害性排序的最终目的是选择危害性靠前的故障模式或产品进行优先改进,实际上也是一个决策问题。张元[29]指出不确定条件下的决策不存在一个通用的普适性标准,目前最理想的做法是根据不同环境选取不同准则。因此排序规则需考虑不同产品分析人员的心理标准和产品特性。

基于已知实核点的情形,在对矩域灰点排序时,可遵照下列规则。

规则 1若矩域灰点Θi的实核点相较于矩域灰点Θj的实核点在效用方向上的投影点更靠近效用方向的终端,则矩域灰点Θi优于矩域灰点Θj,记ΘifΘj;

规则 2若两者投影点重合时,则采用不确定型决策方法讨论。

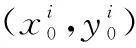
(5)

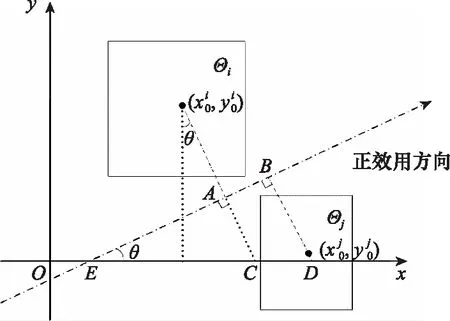
图4 实核点投影不同的矩域灰点排序Fig.4 Sorting of grey points in rectangular region with different solid kernel point projections

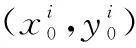
定义 6超额可能效用区域内所有点对期望效用点的效用差之和称为超额可能效用。

超额可能效用的含义是决策者可能获得超过期望效用值的那部分效用,是超出心理预期的额外可能所得。依据定义6,可求得超额可能效用区域Mi的超额可能效用为

(6)

相反地,考虑决策者可能获得少于期望效用值的那部分效用,类似引出差额可能效用相关定义。

定义 8期望效用点对差额可能效用区域内所有点的效用差之和称为差额可能效用。计算式为

(7)

对规则2情形进行分析,如图5所示,持乐观准则的决策者更倾向于超额可能效用更高的选择,所以当

∬ΜiΔUdxdy>∬ΜjΔUdxdy

(8)

有ΘifΘj。当

∬NiΔUdxdy>∬NjΔUdxdy

(9)

成立时，持悲观准则的决策者认为ΘifΘj。

取乐观系数α,当

α∬ΜiΔUdxdy+(1-α)∬NiΔUdxdy>

α∬ΜjΔUdxdy+(1-α)∬NjΔUdxdy

(10)

持折中准则的决策者认为ΘifΘj。

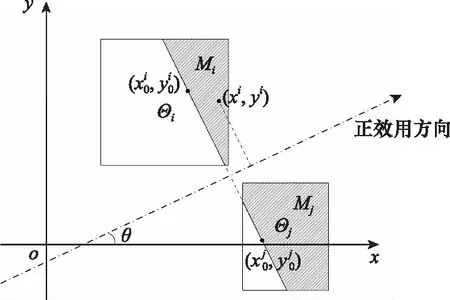
图5 实核点投影相同时的矩域灰点排序Fig.5 Sorting of grey points in rectangular region with same solid kernel point projections

回到CA中,由于危害性矩阵图的危害性是负面效用,因此正向效用方向应取45°斜对角的反方向,即θ=5π/4,再根据式(5)～式(10)可得到故障模式或产品的危害性大小排序。

2.2.2 无相同历史故障信息情形的排序

当无相同故障信息作为参考时,需充分利用相似故障信息。由专家选定相似历史故障信息并提取相应故障参数。由于相似历史故障信息不能等同于被分析故障对象,因此此时故障信息无客观信息支撑,故障模式在危害性矩阵图上以虚核矩域灰点的形态呈现。类似地,同第2.2.1节中规则,由于核点是矩域灰点的位置代表,所以优先比较核点的效用值,若核点效用值相同则继续按不确定型决策方法讨论。当无相同故障信息时所谓的核点,是人们假想的平均化的位置点,并非客观事实所得,故而称之为虚核点。在没有足够可信的信息依靠时,决策者不存在心理上的期望效用值,因此也不存在超额效用。秉持“以防万一”的思想,对矩域灰点排序考虑下列极端情况。

虚核点在正效用方向上投影相同时,无分布信息的矩域灰点在二维空间中沿某一效用递增方向的排序规则推导如图6所示。

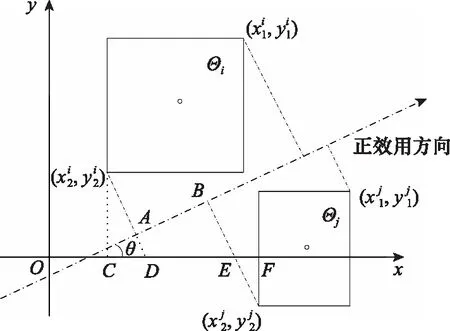
图6 虚核点投影相同的矩域灰点排序Fig.6 Sorting of grey points in rectangular region with samevirtual kernel point projections

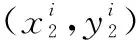
(11)

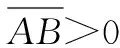
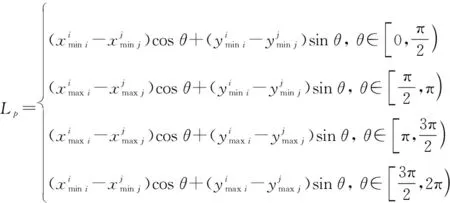
(12)

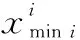
同理,若决策者持乐观准则,往往会考虑最好的情况,即最大的效用可能点。于是类似地可以得出乐观决策者对矩域灰点Θi和Θj的排序规则:

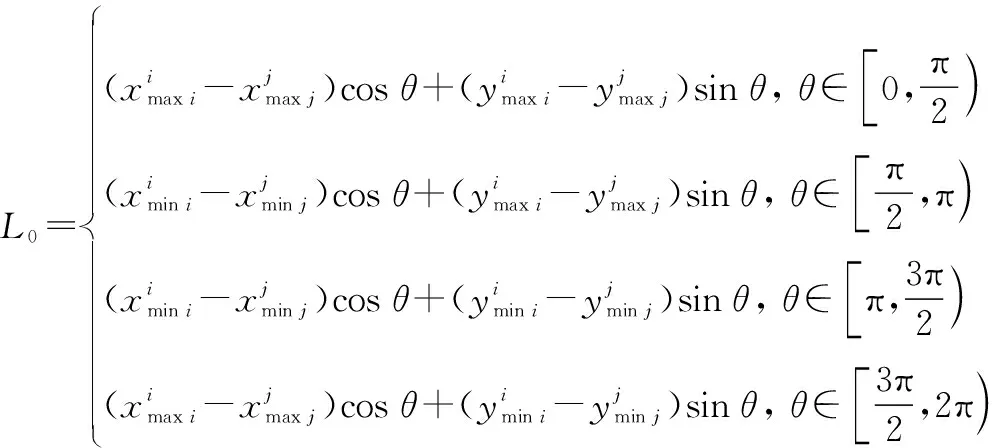
(13)

当L0>0时，称矩域灰点Θi优于矩域灰点Θj。

若决策者持折中准则,则取乐观系数α,可得折中决策者对矩域灰点Θi和Θj的排序规则:

Lh=αLo+(1-α)Lp

(14)

当Lh>0时，称矩域灰点Θi优于矩域灰点Θj。

在本文CA中,由于危害性矩阵图的危害性是负面效用,因此正向效用方向应取45°斜对角的反方向,即θ=5π/4,再根据式(12)～式(14)可得到故障模式或产品的危害性大小排序。

2.2.3 混合故障信息类型情形的排序

混合故障信息类型的危害性排序包括3种情况:有相同信息-无相同信息、有相同信息-确定信息、无相同信息-确定信息。其在危害性矩阵图中对应的形式是:含实核点的矩域灰点-含虚核点的矩域灰点、含实核点的矩域灰点-确定点、含虚核点的矩域灰点-确定点。同样地,优先对核点进行排序比较,因为核点是矩域灰点的位置代表。确定点则可以看作核点是该点的一类白点。若核点在效用方向上的投影重合,则仍采用不确定型决策方法讨论。

对于有相同信息-无相同信息情形,如图7所示,矩域灰点Θi含实核点,而矩域灰点Θj含虚核点。考虑到实核点是以客观信息为依据的期望位置点,而虚核点是假想点,矩域灰点Θj的期望位置点并不一定处于虚核点处,而是可能位于矩域内的任何位置。因此分3种情况讨论:若决策者持乐观准则,认为矩域灰点Θj的期望位置点的效用值大于矩域灰点Θi的实核点效用值,则ΘjfΘi;若决策者持悲观准则,认为矩域灰点Θj的期望位置点的效用值小于矩域灰点Θi的实核点效用值,则ΘifΘj;若决策者持折中准则,认为矩域灰点Θj的最可能位置点的效用值与矩域灰点Θi的实核点效用值差不多,则需进一步考虑实核矩域灰点的超额可能效用和差额可能效用。显然,图7中Θi的差额可能效用比超额可能效用大,所以ΘipΘj。

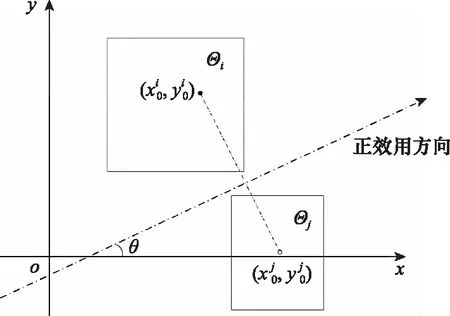
图7 实核点-虚核点投影相同时的矩域灰点排序Fig.7 Sorting of grey points in rectangular region with same solid kernel point and virtual kernel point projections respectively

对于有(无)相同信息-确定信息情形,其在危害性矩阵图中对应的形式是含实(虚)核点的矩域灰点-确定点,这两类情形容易比较。若矩域灰点Θi的实(虚)核点效用值大于确定点(x,y)的效用值,则Θif(x,y);若矩域灰点Θi的实(虚)核点效用值小于确定点(x,y)的效用值,则矩域灰点Θip(x,y);若矩域灰点Θi的实(虚)核点效用值等于确定点(x,y)的效用值,则对乐观决策者而言Θif(x,y),对悲观决策者而言Θip(x,y),对折中决策者而言就进一步考虑实(虚)核矩域灰点的超额可能效用和差额可能效用。

2.3 建模步骤

根据前述分析,适用于贫信息背景的灰FMECA模型建模步骤如下。

步骤 1收集故障信息进行FMEA分析,划定严酷度级别细分标准。

步骤 2收集历史故障信息,由专家给出故障参数的大致范围,以区间灰数表示。依据式(2)～式(4)计算故障模式危害度和产品危害度。

步骤 3选定危害度权重比,依据有无相同历史故障信息判断矩域灰点类别,绘制规范化的危害性矩阵图。

步骤 4依据产品特征选定决策准则,基于第2.2节的矩域灰点排序规则计算改进优先次序,找出改进优先级高的故障模式或产品,填写FMECA报告。

3 案例研究

航天飞机主发动机的高压燃料涡轮泵是航天飞机推进系统中可重复使用次数最少的组件,其昂贵的价格和低复用性属于小样本、贫信息特征,在生产初期运用FMECA找出系统薄弱环节可以大幅减少后续损失。高压燃料涡轮泵主要由涡轮叶片、泵叶轮、密封件、轴承以及壳体等部件组成,确定任务剖面为发动机全寿命期,选取初始约定层次为高压燃料涡轮泵,最低约定层次为主要组成部件。

步骤 1收集高压燃料涡轮泵的故障信息,包括故障模式、任务阶段、故障原因、故障影响以及预防措施,制定细分的严酷度级别标准。由专家给出每个故障模式的严酷度大致位置范围,用含最小制图单位U的区间灰数表示,制作FMEA表如表1所示。

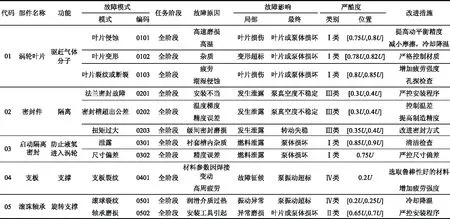
表1 高压燃料涡轮泵FMEA表

步骤 2基于区间灰数计算高压燃料涡轮泵的故障模式危害度和产品危害度。以故障模式0101为例,专家给出故障参数分别为α1=0.42,β1=[0.3,0.4],λp=[16.4,18.61]×10-6/h,t=0.5 h,由式(4)建立规划模型：

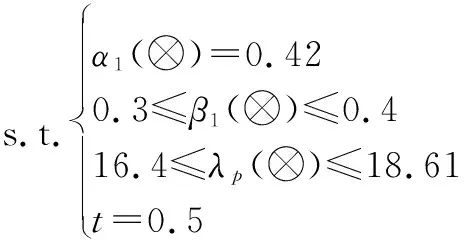
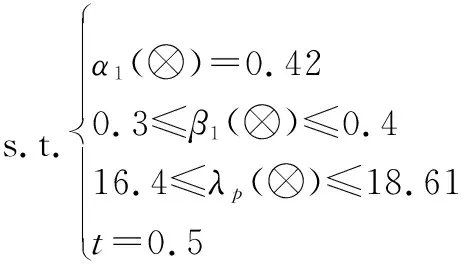
解得故障模式0101的危害度取值范围为Cm1∈[1.033 2,1.563 2]。同理可求得其余故障模式和产品的危害度,制成CA表,如表2所示。

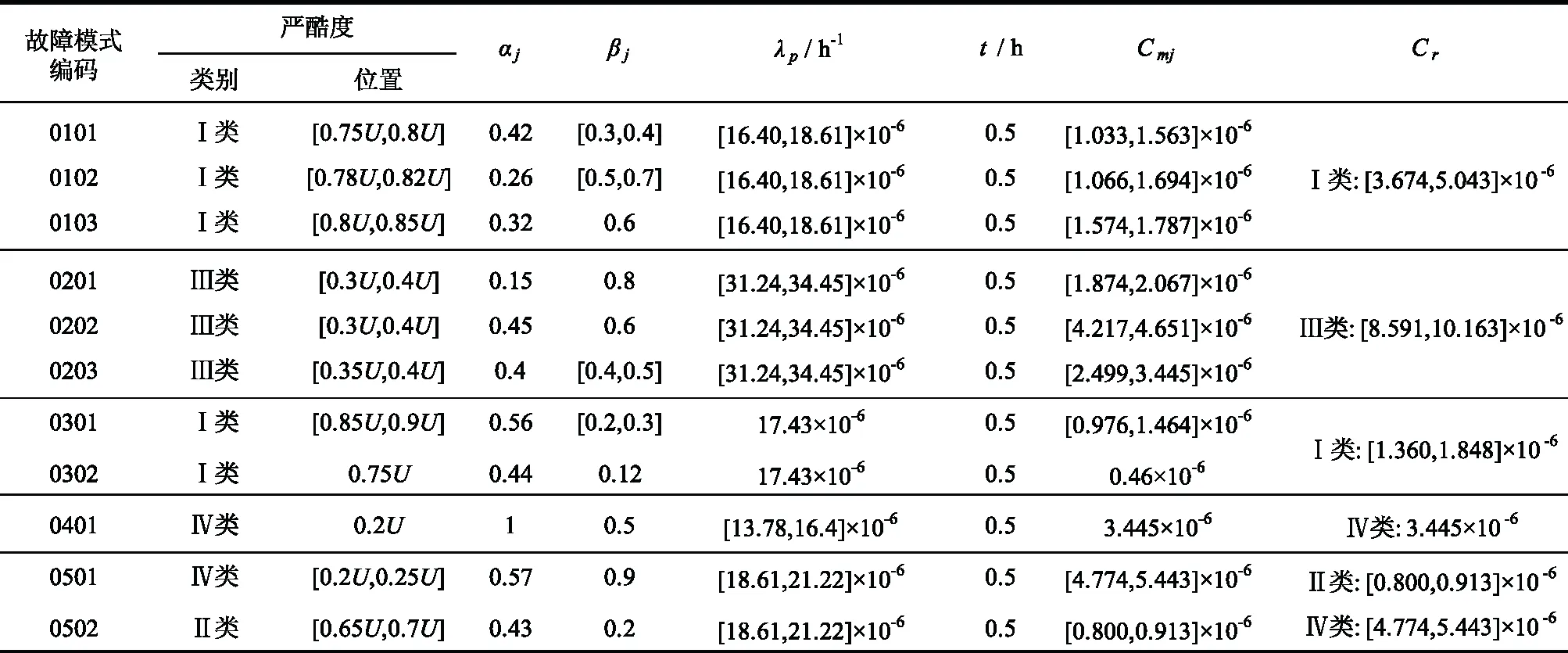
表2 高压燃料涡轮泵CA表

步骤 3考虑到分析对象是用于航天飞机的高压燃料涡轮泵,对故障后果、严酷度更加看重,因此选定危害度权重比kw=0.6,以悲观准则进行决策。依据有无同类故障信息判断矩域灰点类别,得到绘制的规范化危害性矩阵图如图8所示。

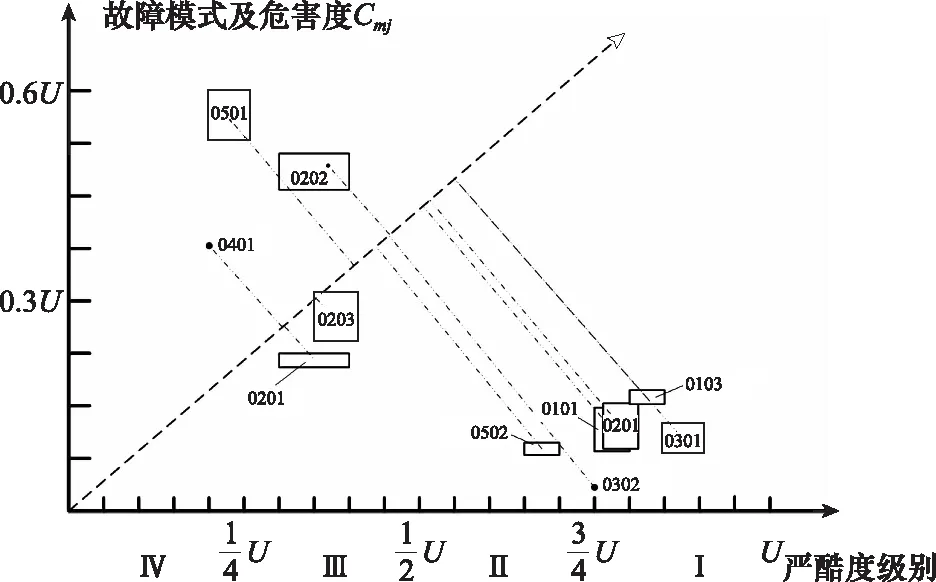
图8 高压燃料涡轮泵规范化危害性矩阵图Fig.8 Standardized criticality matrix diagram of high-pressure fuel turbopump

步骤 4依据产品特征选定决策准则,基于第2.2节矩域灰点排序规则计算改进优先次序。图8中故障模式0103和故障模式0301、故障模式0302和故障模式0202的核效用分别相等,分别依据式(12)和第2.2.3节内容可判断出改进次序:故障模式0301先于故障模式0103,故障模式0202先于故障模式0302。由图8可知,高压燃料涡轮泵中危害性较大的故障主要集中在涡轮叶片当中,其次是密封件和启动隔离密封。其中启动隔离密封的泄露故障模式(0301)危害性最大,是系统的薄弱点,须着重防范。

4 结 论

针对贫信息背景故障信息少、故障数据不确定的情形,提出灰FMECA模型,以解决贫信息背景下FMECA工作的推进困难问题。本文引入区间灰数进行危害度计算,为改进传统危害性矩阵图的缺陷设计新的规范化危害性矩阵图。进而,在规范化危害性矩阵图中提出矩域灰点概念,以分析故障模式和产品在规范化危害性矩阵图中的改进次序。最后,选取火箭高压燃料涡轮泵作为复杂装备领域的贫信息背景代表,结合数值算例运用本文所提的灰FMECA模型。结果表明:贫信息背景对FMECA工作的推进造成了阻碍,结合不确定型决策方法使用灰FMECA模型能解决此类问题。同时注意到,不同的决策准则和危害度权重比参数会对最终的危害度排序结果造成一定影响,所以在运用本文所提模型时应充分考虑被分析对象的特点,对不同用途的产品运用灰FMECA模型时应合理采取决策准则,谨慎选取危害度权重比。由于实际工程产品类型多样、用途迥异,因此如何针对不同类型产品确定决策准则和危害度权重比将是下一步要研究的问题。