基于EAS+MADRL的多无人车体系效能评估方法研究
2021-11-29郭齐胜董志明杨绍卿
高 昂, 郭齐胜,*, 董志明, 杨绍卿
(1. 陆军装甲兵学院演训中心, 北京 100072; 2. 国防科技创新研究院, 北京 100071)
0 引 言
无人作战系统通过优异的战场表现获得了巨大的发展动力,无人作战开始步入战争舞台[1]。美陆军首套下一代战车由6台试验原型机组成,于2019年底交付,2020年初开始试验,2028~2035年之间实现下一代战车的正式应用[2]。美国陆军认为,下一代战车在与实力相当的对手开展的近战中必须具有优势和决定性杀伤力。为达到这一目的,美军开始运用人工智能技术发展战车自主能力,不仅要求作战人员遥控驾驶战车向目标实施火力打击,同时要求战车具备优秀的自主作战能力。多无人车(multi unmanned ground vehicle,MUGV) 协同作战具有增加信息感知量、提高任务完成率、缩短任务完成时间等优势,将成为未来作战的主要样式[3]。效能是武器装备体系在特定作战约束条件(包括作战环境、作战条件、作战威胁等)下,完成规定作战使命任务效果的度量,对应的是其能力的匹配程度。能力描述的是体系固有的本领,是静态的概念,效能是能力发挥出来的效果。体系效能与作战过程有关,具有整体性、动态性、对抗性,是体系在对抗条件下完成具体任务的效能[4-5]。武器装备需求论证是为装备发展提供决策依据的研究工作,研究对象是未来要发展的装备要求,输入是作战单元的使命任务,输出是满足使命任务需求的装备需求方案。武器装备体系效能评估是基于对抗进行武器装备体系论证研究的核心问题。本文基于未来作战场景设想,开展近战场景下的MUGV要点夺控、定点清剿等进攻战斗任务体系效能评估问题研究。
1 相关工作
体系效能评估方法包括分为数学解析、不确定性推理、复杂网络、作战环、探索性分析、建模仿真等方法[6],表1为6类典型评估方法对比。近战场景下的MUGV要点夺控、定点清剿等进攻战斗任务属于高动态、交互复杂、状态空间与动作空间维度高的体系对抗问题,以上方法难以适用。
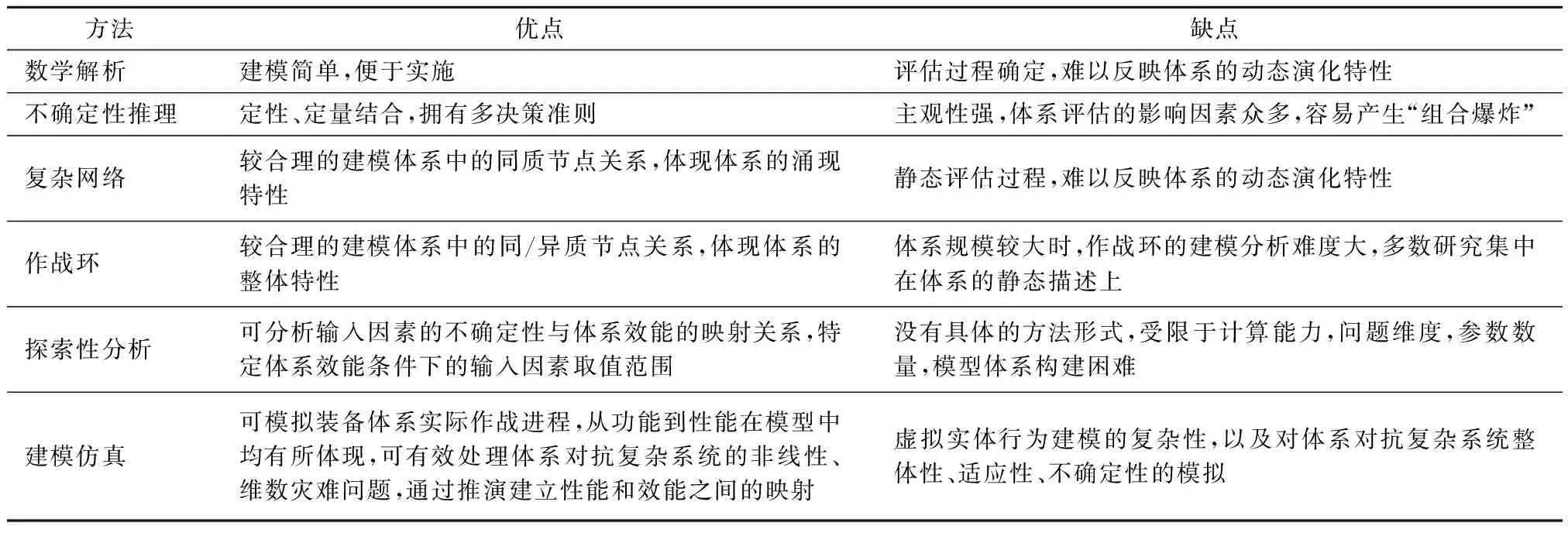
表1 体系效能评估方法对比
探索性分析仿真(exploratory analysis simulation,EAS)是将探索性分析与建模仿真相结合的方法,是基于计算机仿真实验最大限度的模拟体系作战对抗状态,利用大样本空间和定性/定量分析方法探索装备体系作战效能的方法[7],为MUGV体系效能评估提供了可行途径。虚拟实体行为建模方法可分为两大类,一是将战术对抗复杂系统运行规律的理解模型化,并使用公式将各种因素综合权衡的传统方法[8-9],二是直接对战术对抗复杂系统运行规律的认知进行建模的自主学习方法,该方法以多智能体深度强化学习类(multi agent deep reinforcement learning,MADRL)方法为代表,构建认知智能体,让智能体自动学习和获取复杂系统深层次的规律,相较于传统方法更能体现体系的整体性、动态性、对抗性等特点[10]。
体系效能的发挥不仅与装备性能和装备在作战环境中的可用性、可靠性相关,而且与装备作战过程中使用的策略、完成使命任务所涉及的作战环境、作战对手密切相关,作战对手又包括敌方兵力部署、装备性能、作战使用的策略等。MADRL方法是将MUGV作战过程看作为多个智能体在多种状态下进行的动态博弈,将MUGV体系置于作战仿真环境中,使用随机博弈(stochastic game,SG)框架来形式化多智能体与环境的交互。由于战争的不可重复性,不同的作战过程、体系效能会有所变化,智能体通过与环境交互探索,演化出大量不同的作战过程,从中学习MUGV最优联合策略,最大化多智能体累积联合奖励,探索体系能够发挥出的最大效能。
如图1所示,本文基于探索性仿真分析框架,以自主学习方法为基础,提出EAS+MADRL的MUGV体系效能评估方法。该方法以MUGV最大体系效能为学习对象,以体系效能度量因素确定条件下,MUGV最优联合策略为学习目标,最大化累积联合奖励。通过设计奖励函数,使最大化累积联合奖励与体系效能成正相关关系,考察在输入因素不确定条件下体系效能的变化情况,发现体系效能与输入因素之间的重要关系,探索满足约束条件时各因素的变化情况,探索MUGV最大体系效能。

图1 ESA+MADRL方法思路图Fig.1 Thought diagram of ESA+MADRL method
EAS+MADRL方法步骤如图2所示,从待评估的武器装备体系入手,明确问题背景,武器装备具体应用,建立体系效能指标,构建探索性分析模型,进行仿真实验与探索计算,最后对仿真数据分析,得出高价值评估结论,建立更可信、可用的体系效能评估方法。
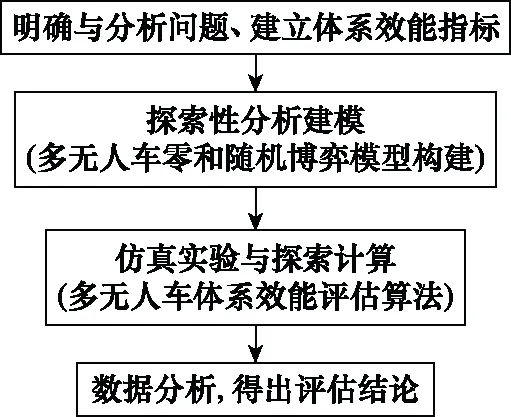
图2 ESA+MADRL方法框架Fig.2 ESA+MADRL method framework
2 基于零和随机博弈的MUGV探索性分析建模
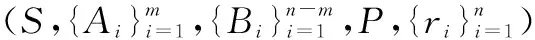

图3 随机博弈过程示意图Fig.3 Schematic diagram of stochastic game process
S为当前博弈的状态空间;Ai为蓝方UGVi的动作空间,A=A1×A2×…×Am表示蓝方m个UGV联合动作空间,i∈[1,m];Bi为红方UGVi的动作空间,B=Bm+1×Bm+2×…×Bn表示红方n-m个UGV联合动作空间,i∈[m+1,n];动作是指UGV在战斗行动中,为完成任务而在一段时间内持续进行的最小操作,是UGV状态转换中分辨率最高、最基本的行为要素。这里动作均指战术动作。空间是由向量组成的一个非空集合。动作空间是一个用来表示UGV战术动作的向量的集合,通过向量间的组合,可以表示出UGV的任何战术动作。联合动作空间是一个用来表示MUGV联合战术动作的向量的集合,通过向量间的组合,可以表示出MUGV的任何联合战术动作。
P∶S×A×B→Δ(S),为状态转移函数,决定了给定任意联合动作a∈A,b∈B,从任意状态s∈S到任意状态s′∈S的状态转移概率。在对抗过程中,P是未知的;ri∶S×A×B→R,为UGVi的奖励函数,定义了当UGV在状态s下,蓝方UGV执行动作a,红方UGV执行动作b,状态s被转换为s′时,获得的瞬时奖励。在t时刻,UGVi根据状态st执行动作ai,t(i∈[1,m])或bi,t(i∈[m+1,n]),系统状态转移至st+1,UGVi获得奖励值ri(st,a(t),b(t)),a(t)=(a1t,a2t,…,ant),b(t)=(bm+1,t,bm+2,t,…,bn,t)。UGVi的目标都是通过找到一个策略πi∶S→Δ(Ai),即ai,t~πi(·|st),来最优化自己的长期奖励。随机博弈中的多个UGV需要选择动作,形成联合动作,并且下一个状态和奖励取决于该联合动作,每辆UGV有自己独立的奖励函数。
2.1 状态空间设计
MUGV的联合状态空间S应包括战场环境、红蓝双方兵力数量、状态等信息,需要从中选择有限维数的关键状态作为S的元素。MUGV保持较好的位置关系并根据对方情况适时进行队形变换、进攻、防御,随时保持在相对于对方最佳的位置进行战斗,方能发挥体系的最大作战效能。因此,将S分为共享状态空间Sshared和局部状态空间Slocal两部分,即S={Sshared,Slocal}。Sshared在UGVS间共享,使得每辆UGV具有全局视野,具体包含表2所示信息。

表2 MUGV共享状态空间设计
Slocal通过UGV探测感知得到,辅助UGV具体动作实施、调整,以UGVi为例,包含表3所示信息。其中,i=1,2,…,m,j=1,2,…,n。

表3 MUGV局部状态空间设计
以上元素值需要进一步规范化,使得联合状态值在合理范围内变动。
2.2 动作空间设计
UGV的动作主要是机动和射击两类,细化为单位时间步长内机动的方向和距离,射击瞄准点的方向和距离。因此,UGV动作空间采用[-1,1]的连续实数变量描述,Ai={p,θ,ρ},p表示执行攻击或移动动作的概率,θ,ρ分别表示执行动作的角度和距离,θ,ρ用极坐标形式表示,用来描述UGV从当前位置执行射击或机动动作的目标点,如图4所示。
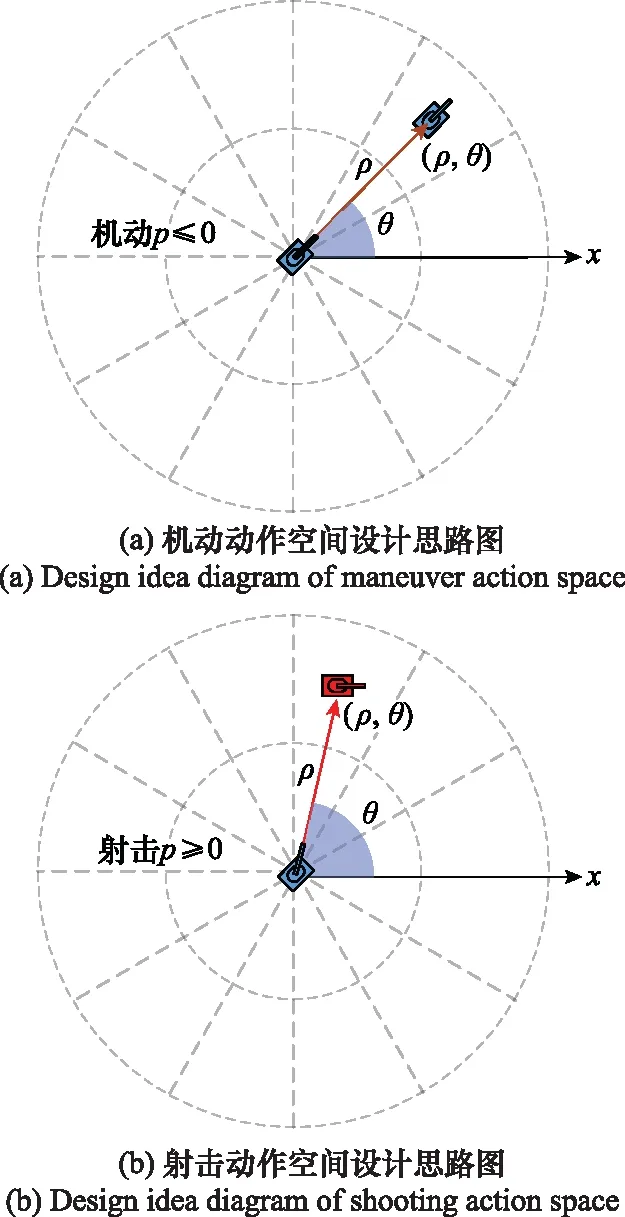
图4 动作空间设计思路图Fig.4 Action space design idea diagram
以UGVi为例,具体表述如表4所示。

表4 UGV动作空间设计
在执行攻击动作时,选择离目标点最近的红方UGV作为蓝方UGV的攻击目标进行攻击。MUGV联合战术动作包括队形展开、发起冲击、集火射击等,为了避免动作空间过大,动作空间设计的原则是用尽可能少的向量参数,表示出尽可能多的战术动作。图5(a)所示为MUGV队形展开战术动作,ρ1,ρ2,ρ3均小于1,说明MUGV此时处于一个较小的范围内;p1,p2,p3均小于0,说明UGV处于机动状态;θ1=30°,θ2=90°,θ3=150°表示车体角度为3个不同的方向。因此,联合动作(a1,a2,a3)表示MUGV正在队形展开。同理可知图5(b)所示为MUGV集火射击动作。
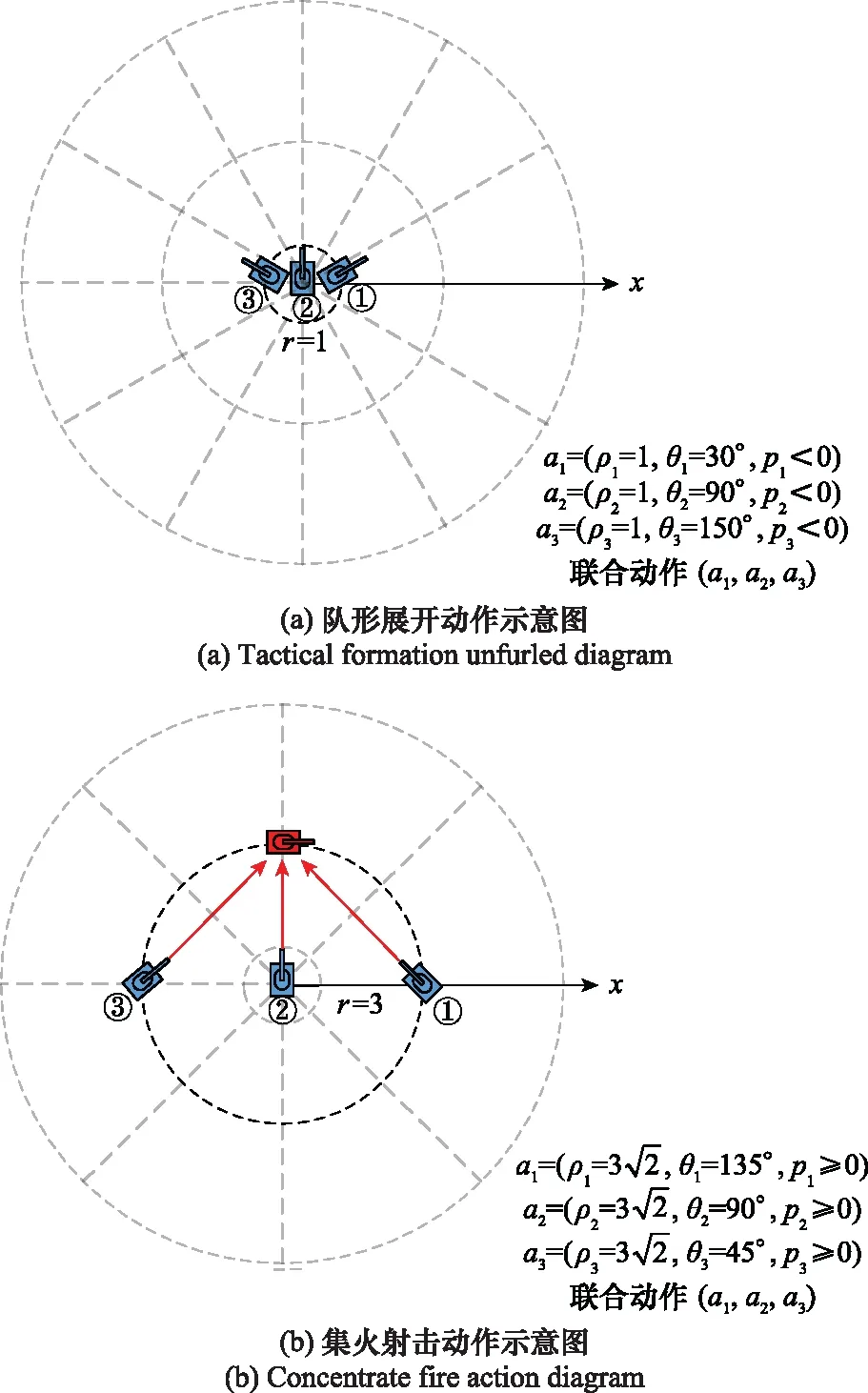
图5 联合战术动作空间设计思路图Fig.5 Diagram of joint tactical action space design
2.3 奖励函数设计
定义蓝方时变全局奖励函数如下所示:
(1)

3 面向MUGV体系效能评估的探索性算法
本节分别对MUGV作战效能评估探索性算法原理进行分析和设计。
3.1 算法原理

(2)
式中:π-i=[π1,…,πi-1,πi+1,…,πn]表示除去i之外的UGV的联合策略。在NE,每个UGV的策略是其他UGV联合策略下的最优策略。MUGV控制本质上可以看作是寻找对整个体系的最优控制策略。通过探索不同红方MUGV规模条件下,蓝方MUGV ZSG模型的NE解,以及分析NE条件下参战双方战损比、作战时长等约束,完成MUGV体系效能评估,图6所示为体系效能评估探索性算法步骤图。

图6 体系效能评估探索性算法步骤图Fig.6 Exploratory algorithm step diagram for system effectiveness evaluation
零和随机博弈属于随机博弈,同时,零和随机博弈的所有状态必须定义为一个零和矩阵博弈。随机博弈的解,可以描述为一组关联特定状态矩阵博弈中的NE策略,零和博弈的NE是一种最大化值函数策略。因此,在每个特定状态矩阵博弈的NE策略的集合为零和随机博弈最优策略[14-15]。图7所示为零和随机博弈最优策略求解思路图,通过强化学习方法架起多智能体系统与寻找NE的桥梁。
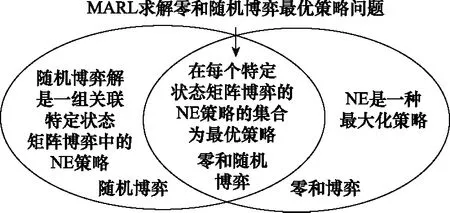
图7 零和随机博弈最优策略求解思路图Fig.7 Optimal strategy solution diagram of zero sum stochastic game

(3)
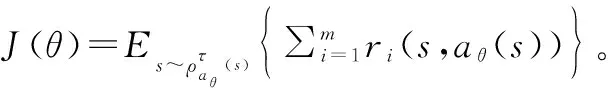
(4)
3.2 算法设计
步骤 1初始化红方UGVS规模,蓝方UGVS Actor网络θ和Critic网络ξ,目标Actor网络θ′←θ和Critic网络ξ′←ξ,经验缓存池D。设置最大探索批次(maxepoch),每批次(epoch)包括N次作战过程演化,每次作战过程最大仿真步长T。
步骤 2针对每次作战过程演化,执行以下操作:
步骤 2.2初始化随机过程μ用于动作探索;
步骤 2.3接收初始观察空间s1;
步骤 2.4针对每个仿真步长t,执行以下操作:
步骤 2.4.1针对每辆UGV,选择和执行动作ai,t=ai,θ(st)+μt;
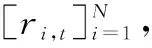
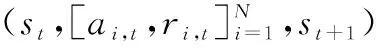
步骤 2.4.4从D中随机采样M个状态转换过程;
步骤 2.4.5使用双向循环神经网络计算每个转换过程中每个智能体的目标值,对M个状态转换过程,执行下式操作:
(5)
步骤 2.5计算UGVCritic网络梯度估计,如下所示:
(6)
步骤 2.6计算UGV Actor网络梯度估计,并采用Critic网络梯度估计代替Q值,如下所示:
(7)
步骤 2.7采用Δξ,Δθ梯度估计和Adam方法更新UGV Actor、Critic网络。
步骤 2.8更新UGV目标网络,如下所示:
ξ′=γξ+(1-γ)ξ′,θ′=γθ+(1-γ)θ′
(8)
步骤 3红方UGVS是否被完全击毁,如果是,转入步骤4,否则,调整UGVS规模,转入步骤1。
步骤 4输出作战效能指标。
4 应用示例
如图8所示,场景设想在2030年,美俄争霸在叙利亚地区冲突再起,双方将大量新型武器投入战场。在美国的支援下,反政府武装(蓝军)占领了叙利亚政府广场,宣告胜利,并操控无人战车(6台)组成了严密的火力网。政府军(红方)在俄罗斯的支援下,决定整建制使用自主作战无人战车连进行攻坚战,目的是消灭蓝军战车,夺回蓝军占领要点。现要求论证红方无人战车连在未来场景设想下的UGV规模。
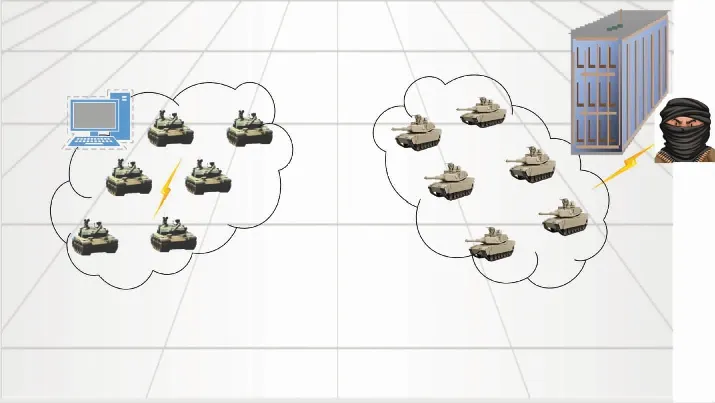
图8 MUGV对抗场景示意图Fig.8 Schematic diagram of MUGV confrontation scene
4.1 实验设置

(9)
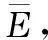

表 5 UAV属性值设置

图9 距离要素量化示意图Fig.9 Distance element quantification schematic diagram
体系效能是针对对手装备体系及其采用的策略μ来说的,是一个相对量。设置蓝方的策略μ为“就近攻击”,即在每次行动决策时,总是操控UGV选择离其最近的目标先敌开火,单位时间步长内最多可同时控制6台UGV。
4.2 实验结果与分析
由epoch=150,N=20可知,总共进行了3 000次作战过程的演化探索,其中图10~图12所示分别为红方体系效能区间分布、红方胜率区间分布、红方最大体系效能值随其UGV规模变化情况。通过对实验结果分析,可得出以下结论。
(1) 体系效能更可能服从一个分布,而不是一个固定值。复杂系统结构动态可变,过程涌现不可预测,结果不重复,但又表现出总体的规律性,不以人的意志为转移。给体系效能指标一个最终量化值可能无法完全概括体系的性能,或者无法完全说明问题,体系效能的指标量化更有可能是从推演产生的数据中得出的一个概率分布。由于基于自主学习的虚拟实体具有作战能力等级,并且产生的行动序列具有多样性,因此可以模拟出复杂系统的适应性、涌现性、不确定性,进而产生的数据更贴近复杂系统运行规律。基于规则的虚拟实体生成方法,作战行动序列较为固定,能力等级不明确,因此,产生的数据无法很好反应复杂系统规律。
(2) 体系中并是不装备的数量越多越好,随着装备数量的增加,体系能力增强,同时也意味着更多战损,指控难度增加。由图10可以看出,当UGV数量为6时,释放的体系效能值大部分在[20,30)区间,当UGV数量为7时,释放的体系效能值大部分在[0,10)区间。同时,由图11可知,当UGV数量为6时,落在[0.8,1]胜率区间有80个批次,UGV数量为7时有50个批次,图10与图11相互印证。
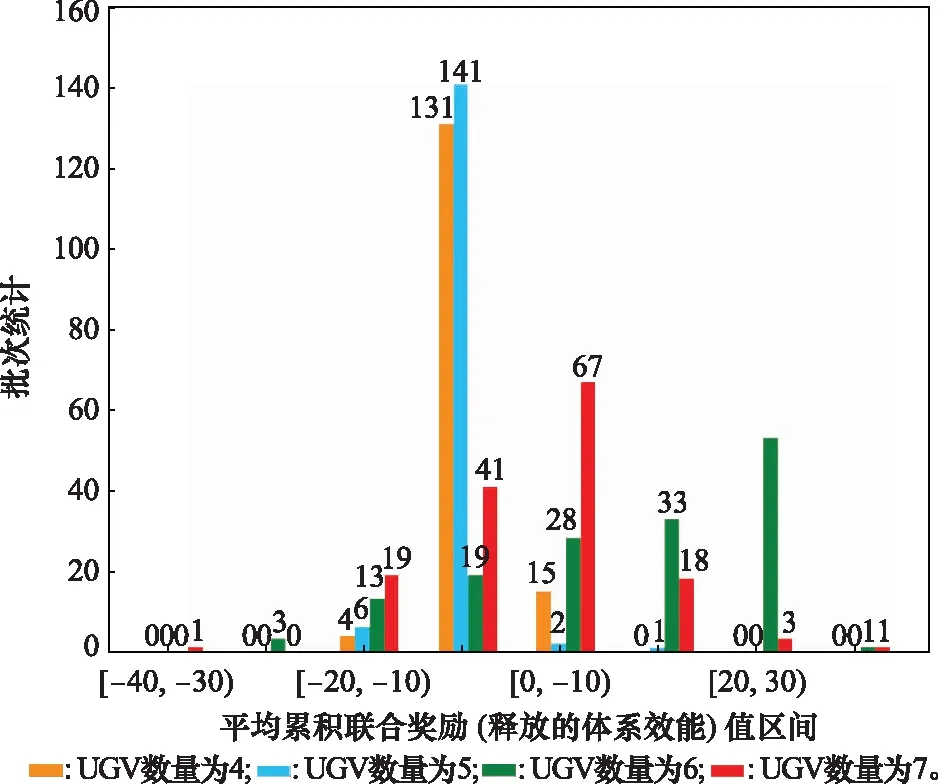
图10 红方体系效能区间分布图Fig.10 Distribution diagram of efficiency interval of the red side
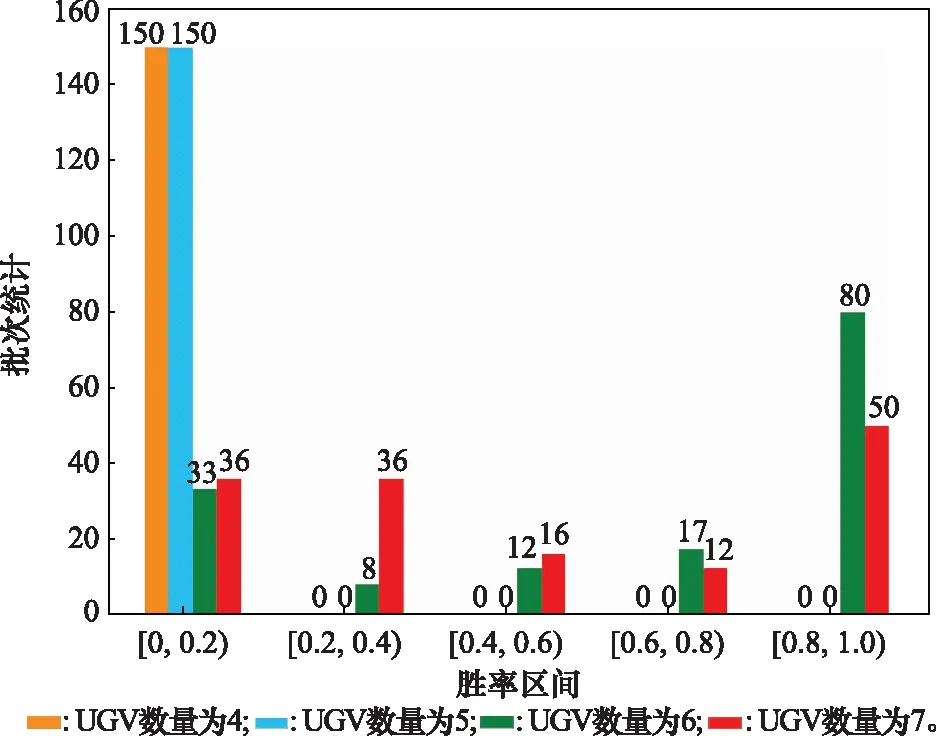
图11 红方胜率区间分布图Fig.11 Distribution diagram of winning rate interval of the red side
(3) 最大体系效能值随UGV数量呈非线性变化,当UGV达到一定数量时,释放的最大体系效能会发生由量变到质变的变化。由图12可知,当UGV数量由4辆增加至5辆时,释放的最大体系效能增加4.27,当UGV数量由5辆增加至6辆时,释放的最大体系效能增加25.57,此时,最大体系效能发生了骤增,1辆UGV之差,最大体系效能增加至约是原来的3.12倍。当UGV数量由6辆增加至7辆时,释放的最大体系效能增加1.87,最大体系效能达到了“瓶颈期”,没有发生太大变化。
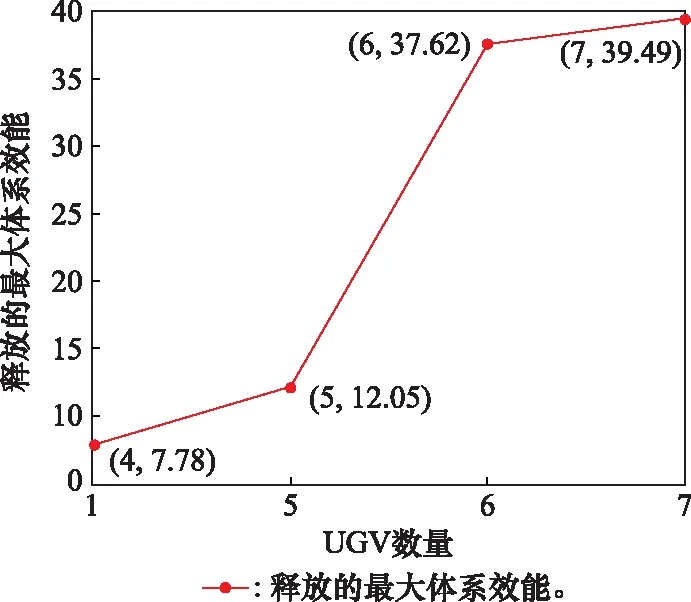
图12 红方最大体系效能变化图Fig.12 Changes of maximum system efficacy of the red side
图13为UGV数量为5时的一些典型战斗场景,图13(a)为MUGV集火攻击战术场景,图13(b)为MUGV边打边撤的游击战术场景,无论哪种战术,释放的体系效能都无法战胜对手MUGV体系。这与图10红方胜率区间分布图中,UGV数量为5时,胜率分布全部在[0,0.2)区间相互印证。图14为UGV数量为6时的集火攻击战术典型战斗场景,图15为UGV数量为7时的包围战术典型战斗场景,可以看出,此时释放的体系效能完全可以战胜对手MUGV体系。

图13 UGV数量为5时的战斗场景Fig.13 Combat scene when UGV number is 5

图14 UGV数量为6时的集火攻击战术战斗场景Fig.14 Concentrated fire attack tactical combat scene when UGV number is 6

图15 UGV数量为7时的包围战术Fig.15 Surrounding tactical combat scene when UGV number is 7
综上分析可知,红方UGV连在未来场景设想中,蓝军遥控远程6辆M型UGV,采用矩阵队形进攻,以及就近攻击策略条件下,规模为6辆M型UGV。
5 结 论
本文针对MUGV体系效能评估问题,建立了一套以自主学习方法为基础的探索性仿真分析方法。由于方法以零和随机博弈模型为基础,双方UGV为完全竞争对抗关系,因此,方法适用于未来UGV要点夺控、定点清剿等进攻战斗近战场景下的体系效能评估问题。通过探索不同UGV规模条件下,模型一方的NE解,以及分析纳什均衡条件下参战双方战损比,作战时长等约束,完成MUGV体系效能分析。由于是探索模型一方的NE解,因此,假想敌一方的策略需要服从固定分布。这要求在装备体系论证过程中,对假想敌UGV的技术路线、作战条令等有所了解,从而对策略做出合理假设,例如假想敌的UGV采用就近攻击、先敌开火的作战条令原则,或UGV是采用了某种算法。由于实际作战过程是非完全信息博弈,本文采用的模型假设作战过程是完全信息博弈,双方装备对抗体系已知,因此,方法主要面向装备论证领域,不适用于实际作战领域。
