基于频域互相关序列与峰值检测的空频分组码盲识别算法

闫文君, 张聿远,*, 凌 青, 于柯远, 谭凯文, 刘恒燕

(1. 海军航空大学航空作战勤务学院, 山东 烟台 264001;2. 中国人民解放军92853部队, 辽宁 兴城 125100)

0 引 言

信号识别技术一直是近几年研究的热点和难点,特别是在频谱资源日益紧张的信息时代。随着频谱资源的紧缺,多载波技术以其频带利用率高和抗多径干扰能力强等优点而得到了越来越广泛的应用,因此多载波多天线识别技术也成为研究的热点。近些年多载波技术与空间编码(space block coding, SBC)相结合,已经成为IEEE 806.12n和IEEE 806.12e核心技术[1],广泛应用在第4代移动通信中。现阶段对于SBC识别方法的研究通常是在单载波的条件下,多载波条件下识别算法较少。在考虑多载波的情况下,SBC与正交频分复用(orthogonal frequency division multiplexing, OFDM)结合有两种方式,一种是把数据符号先OFDM编码然后再空时编码(space time block code, STBC)[2-6],一般称之为STBC-OFDM[7-8]。还有一种即为本文所研究的空频分组码(space-frequency block code, SFBC)信号,先进行SBC编码,然后再进行OFDM编码[9-13],一般称之为SFBC-OFDM。

目前,研究STBC-OFDM信号发射端编码方式识别的文献相对较多,主要的方法包括统计特性[14-17]、K-S检测[18]和四阶滞后积(fourth order lag product, FOLP)[19-21]等,从识别效果来看,以上算法[14-21]的识别效果较理想,算法的鲁棒性也较强。但由于SFBC的编码方式较为复杂,因此针对SFBC-OFDM信号识别问题文献相对较少[9-13]。其中,文献[9]是在时域上对信号进行识别,首先对接收信号按照OFDM块的大小进行分组,对每组信号分别求取自相关函数,再求取各组之间自相关函数的均值。由于STBC的相关性,在时域上,空间复用(spatial multiplexing, SM)信号和AL(Alamouti)信号呈现不同的均值特性,从而达到识别的目的。文献[10]基于随机矩阵理论(random matrix theory, RMT),在频域内通过滑动窗口检测主成分序列,并将其欧式距离作为决策特征。文献[11]通过对接收信号在不同OFDM子载波处的信号子空间和噪声子空间进行分离得到辨识特征,并根据噪声子空间的最大特征值确定决策边界,实现SFBC识别。文献[12]基于中心极限定理(central limit theorem, CLT),利用空间域冗余计算估计量的互相关函数,构造卡方统计量作为识别决策量。文献[13]提出了一种基于二维空频冗余(two-dimensional space-frequency domain redundancy, TDSFDR)的SFBC识别方法,利用空频冗余构造估计器的互相关函数,在假设检验统计量中加入频域冗余以实现识别。以上算法[9-13]的识别效果较好,但由于需要对接收信号按照OFDM块长度进行分组,因此需要知道两点先验信息:一是OFDM块长度;二是接收信号和发射信号的同步信息,即接收信号和发射信号对应关系。这两点在通信侦察领域显然不容易满足。此外,上述算法[9-13]的特征提取流程繁琐,耗时较长,不利于满足实际通信环境中精准快速识别的现实需求。

为解决非协作通信和复杂电磁环境中SFBC的识别问题,本文提出了一种基于频域互相关序列和峰值检测的SFBC盲识别算法。首先通过分析SFBC信号的编码特点,计算得到发送端的互相关函数;然后考虑频率选择信道、多径传播和噪声的影响,推导了接收信号的互相关函数,并且对其进行傅里叶变换得到频谱图;最后根据频谱图检测其峰值位置识别信号类型。该算法不需要知道信道信息和OFDM块长度,不要求接收端与发射端时钟同步,更加适用于非协作通信。仿真实验表明,该算法对时间偏差和频率偏差等情况的适应性较强,在复杂电磁环境下具有较好的识别性能,能够应用在认知无线电和频谱检测等场合。

1 信号模型和假设条件

1.1 信号模型

对SM通信系统,将长度为2N的数据集d进行分块,以块为单位在两个天线上发射,第b块数据集通过SM[22-27]生成两个新的数据向量q为

q(b,0)=[d(b)(0),d(b)(2),…d(b)(2N-2)]

(1)

q(b,1)=[d(b)(1),d(b)(3),…d(b)(2N-1)]

(2)

对于AL通信系统,将长度为N的数据集d进行分块,以块为单位在两个天线上发射,第b块数据向量通过SBC[28-32]生成两个新的数据向量u为

u(b,0)=[d(b)(0),-d(b)*(1),d(b)(2),…,
d(b)(N-2),-d(b)*(N-1)]

(3)

u(b,1)=[d(b)(1),d(b)*(0),d(b)(3),d(b)*(2),…,
d(b)(N-1),d(b)*(N-2)]

(4)

在SBC后,进行OFDM变换,具体方法是:对得到的新数据集u和q做快速傅里叶逆变换,并且加上前缀,可得到OFDM块,当信号为AL编码时x(b,f)为

(5)

当信号为SM时x(b,f)为

(6)

式中:n=-v，…,N-1;f=0,1代表发射天线的编号;u(b,f)(k) 和q(b,f)(k)分别表示u(b,f)和q(b,f)第k个数据符号。

发射信号s由不同块发射信号x(b)组合而成,两个发射天线上信号s(0)和s(1)分别为

s(0)=[x(0,0),x(1,0),x(2,0),…]

(7)

s(1)=[x(0,1),x(1,1),x(2,1),…]

(8)

因此,发射信号经过信道后第i根天线接收信号可以表示为

(9)

式中:i=0,1,…,nr-1;hdi(l)是第d个发射天线和第i个接收天线的信道脉冲响应;n(i)(m)是第m个高斯白噪声信号;s(d)(m)是发射信号s(d)的第m项。

1.2 假设条件和适用性

本文在以下条件下进行仿真实验[33]:

(2) 信号与噪声是不相关的;

(3) 本文算法适用的调制方式为多相移键控(multiple-phase shift keying, M-PSK)和多正交幅度调制(multiple quadrature amplitude modulation, M-QAM)。

2 基于频域互相关序列与峰值检测的SFBC识别

2.1 理论推导

考虑序列y=[y(0),y(1),…,y(K-1)],其中y(k)=r(k)r(k+N/2),k=0,1,…,K-1,K=M-N/2。由于随机变量可以表示为其均值和另一个代表偏差的零均值的变量的和,因此SM和AL信号的y(k)可以表示为

(10)

(11)

依据式(1)、式(2)和式(9)～式(11),由于发射信号是独立同分布的,很容易推导出:

E{ySM(k)}=0

(12)

ySM=[0,0,0,…]

(13)

对于AL信号,详细推导yAL(k)序列的峰值特性。由于SFBC编码与STBC编码的不同,其在不同子载波间进行SBC,因此首先计算发射端的相关函数,结合式(5)可得

E[x(b,0)(n)x(b,1)(n+N/2)]=

(14)

式中:u(b,0)(k0)和u(b,1)(k1)是分别为u(b,0)和u(b,1)向量中第k0和k1个数据;k0,k1变化范围为向量u长度范围[0,N-1]。

由式(14)和文献[33]可知,发射端相关函数的幅值由u(b,1)(k0)和u(b,1)(k1)决定,与之相乘的指数部分主要对该项的符号产生影响。考虑到只有互为共轭的信号才相关,使得其均值不为0,因而可通过分析编码序列的相关性排列进一步对该式进行化简。但与文献[33]所不同的是,本文算法是在频域上实现了SFBC的识别,与在时域上进行SFBC识别的文献[33]相比,不需要接收端与发射端的同步,适用于非协作通信和非时钟同步场景。

以子载波数量N=64为例,不加前缀,u(b,1)(k0)和u(b,1)(k1)互为共轭项的序号k0和k1如表1所示。

表1 序号k0和k1的对应关系

根据表1,由式(14)可得

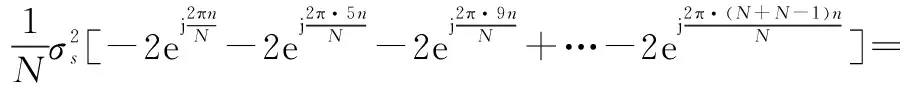
(15)

因式(15)还与指数项有关,因此对该式进一步简化为

(16)

经过信道和噪声后,E{yAL(k)}的表达式为

E{yAL(k)}=E[r(i)(k)r(i′)(k+N/2)]=

E[s(b,d)(k-l)·s(b,d′)(k+N/2-l′)]

(17)

将式(16)代入式(17)进一步化简得

∏(k,k+N/2-l-l′)=

(18)

式中:∏(k,k+N/2-l-l′)代表指示函数,其含义是s(b,d)(k-1)和s(b,d′)(k+N/2-l′)在同一个OFDM块中。

由式(18)可知,E{yAL(k)}在单个子载波周期内有4个峰值,分别在位置为(N+v)n+(l-l′)/2、(N+v)n+N/4+(l-l′)/2、(N+v)n+N/2+(l-l′)/2和(N+v)n+3N/4+(l-l′)/2处。

yAL=[C1,0,0,…,C2,0,0,…,C3,0,0,…,C4,0,0,…]

(19)

式中:C1=-1、C2=-j、C3=1和C4=j,中间是15个连0,因此序列yAL是一个周期函数,其周期为16。

假设Y(n)=[Y(0),Y(1),…，Y(K-1)]是向量y的DFT变换:

(20)

将式(10)和式(11)代入式(20),可得

(21)

(22)

因此可以说明YSM没有峰值,而YAL存在峰值,且每隔K/16有峰值,周期是K/16。

2.2 仿真验证

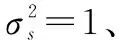
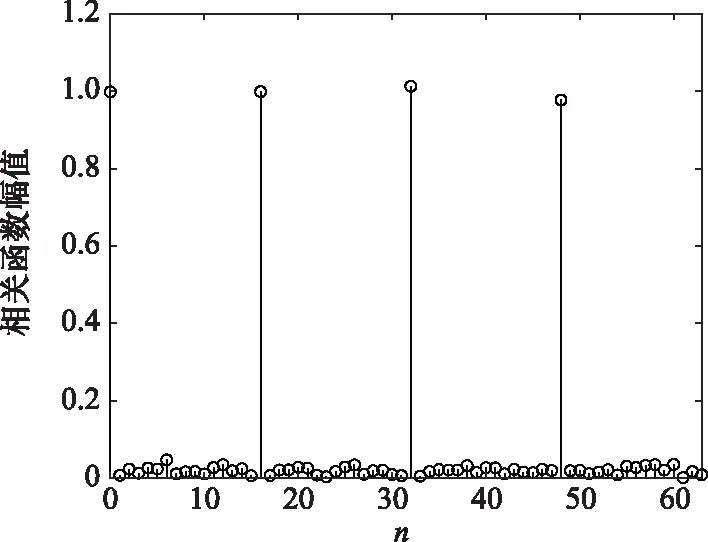
图1 发射端相关函数幅度值Fig.1 Amplitude value of transmitter’s correlation function

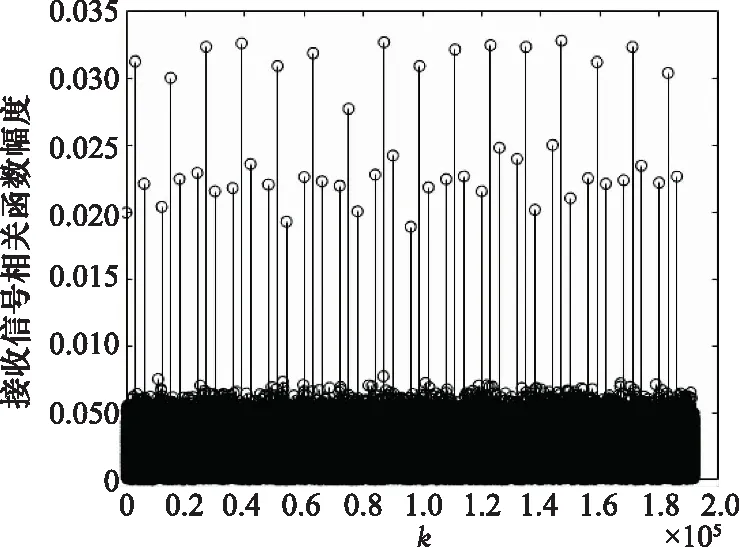
图2 接收端相关函数幅度值Fig.2 Amplitude value of receiver’s correlation function

3 算法流程

通过检测YAL(n)峰值,可以识别SFBC-OFDM信号,具体流程如图3所示。

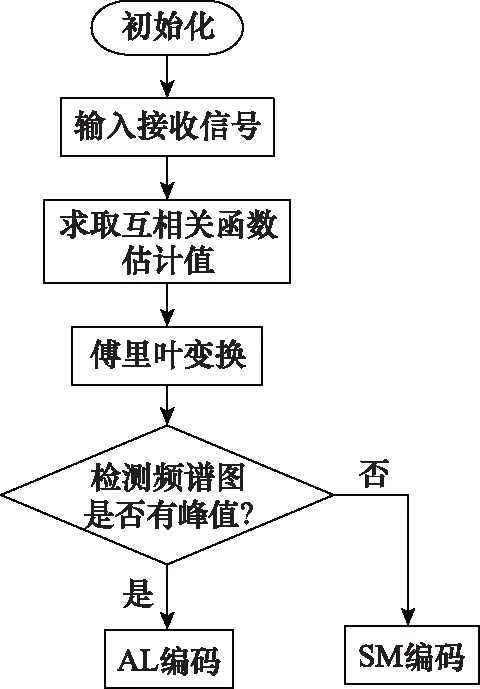
图3 频域互相关序列的峰值检测流程Fig.3 Peak detection process of frequency domain cross correlation sequence

(1) 输入信号:接收信号r(k),k=0,1,…,K。

(2) 由式(17)计算接收信号的互相关函数估计值E{y(k)};

(3) 对E{y(k)}进行傅里叶变换,并绘制得到频域图;

(4) 如果频域图存在峰值,且峰值间距离为K/16,则接收信号为AL编码,若没有明显峰值,则接收信号为SM编码。

4 仿真验证

4.1 实验参数设置

本文对SM和AL编码的SFBC-OFDM信号进行识别,采用QPSK调制和频率选择性信道进行仿真,仿真信道包含Lh=3条独立路径。OFDM块长度为N=64,对应的循环前缀长度设置为v=5,接收端OFDM块数量为Nb=1 000。接收天线数设置为nr=2,仿真数据在-10～15 dB下产生,采用1 000次蒙特卡罗实验得到的平均正确识别概率p(λ|λ)对方法的优劣进行衡量。

4.2 接收天线数对识别性能的影响

如图4所示,算法性能随信噪比的增加而稳步提升,通过增加接收天线可获得明显的性能增益,并且这种增益随着天线数量的增加而趋于饱和。因此,在天线资源较为充裕的情况下,可考虑将接收端天线扩展至2～3个,以较少接收天线数尽可能获得更明显的性能改善。

图4 接收天线数量对识别性能的影响Fig.4 Influence of receiving antennas number on recognition performance

4.3 调制方式对识别性能的影响

为对比不同调制方式对算法性能的影响,本节对算法在不同调制方式(QPSK、8相移键控(phase shift keying, PSK)、16正交幅度调制(quadrature amplitude modulation, QAM)和32QAM)下的性能进行仿真。由图5可知,调制方式对本文算法的准确率影响不大,这是由于SM和AL的互相关序列峰值大小与调制方式无关,SFBC-OFDM的识别特征不受该因素影响,从而使得算法对多种调制方式均适用。

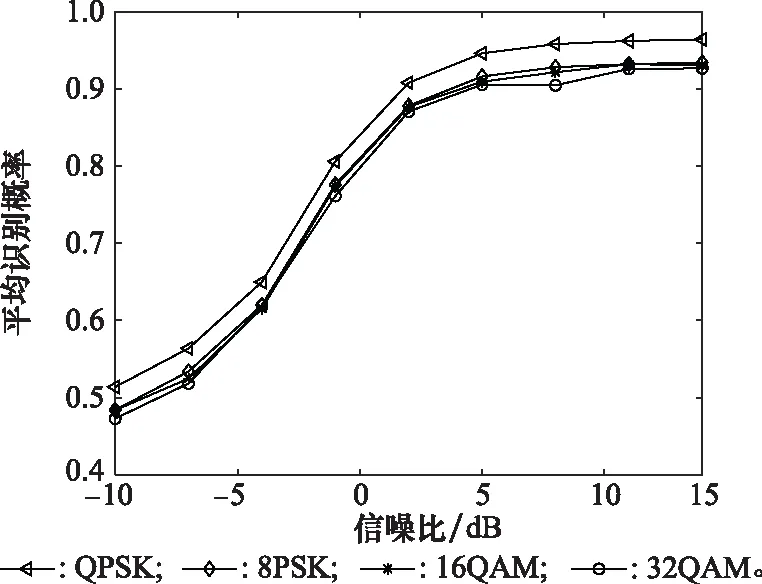
图5 调制方式对识别准确率的影响Fig.5 Influence of modulation mode on recognition accuracy

4.4 时间偏差对识别性能的影响

为分析时间偏差对算法识别性能的影响,本节对不同时偏下的识别准确率图像进行了仿真,实验结果如图6所示。由图6可知,本文算法对时间偏差ξ具有良好的适应性,各时偏下的识别性能稳定,算法的鲁棒性较强,该因素对算法性能的影响不大。

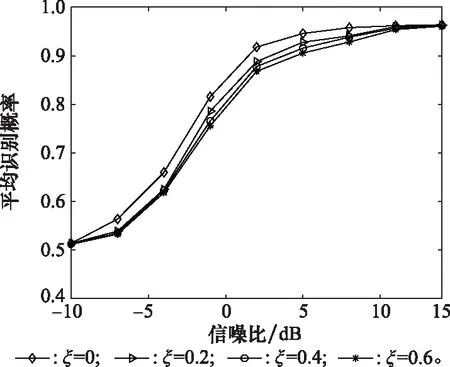
图6 时间偏差对识别准确率的影响Fig.6 Influence of time bias on recognition accuracy

4.5 频率偏差对识别性能的影响

为分析频率偏差对算法识别性能的影响,本节对不同频偏下的识别准确率图像进行了仿真,实验结果如图7所示。其中,频率偏差fc归一化为载波频率。由图7可知,本文算法在频率偏差为fc<10-3时识别效果较好,对频偏具有一定的适应性。

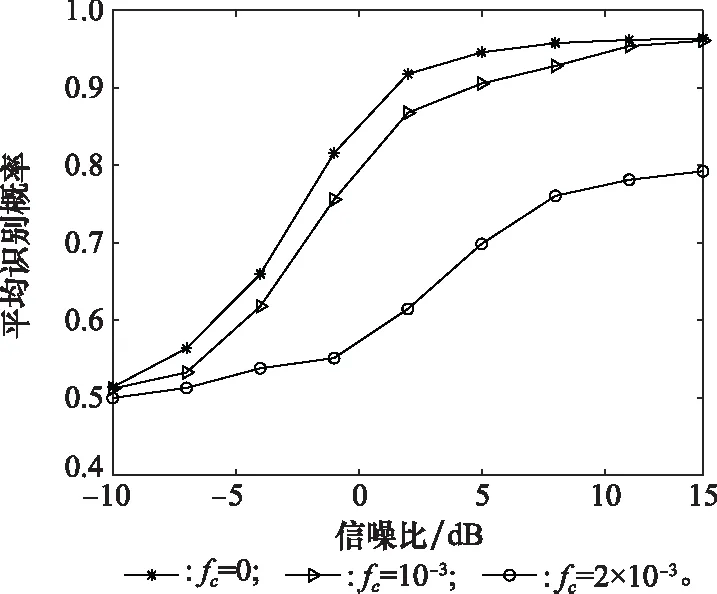
图7 频率偏差对识别准确率的影响Fig.7 Influence of frequency deviation on recognition accuracy

4.6 本文算法与现有算法的性能对比

为衡量本文算法性能,将本文算法与文献[9]在不同OFDM块数量下进行对比,取OFDM块数量Nb={200,500,1 000,2 000}。

如图8所示,本文算法在OFDM块为200和500时性能较差,当OFDM块数量为1 000时,本文算法性能有了明显提升,在识别概率为5 dB时识别准确率达到0.96左右,当OFDM块数量为2 000时,本文算法性能与文献[9]性能差别不大,高信噪比下识别率达到98%左右,低信噪比下性能也较好。

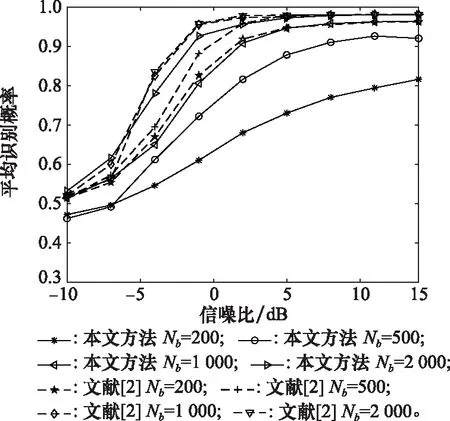
图8 不同算法在各OFDM块数下的识别性能Fig.8 Recognition performance of different algorithms in each OFDM block number

总体来看,本文算法缺点在于所需要的接收信号数更多,优势在于不需要接收信号OFDM块大小和接收端与发射端的同步信息。显然,在非协作通信条件下,扩展信号数量较后者的条件更容易满足,本文算法更适用于电子侦察、频谱检测等应用场景。

5 结 论

本文依据SFBC的相关性,提出了一种基于频域互相关序列和峰值检验的识别方法,较好地解决了非协作通信下的SFBC-OFDM信号识别问题。实验结果表明,本文算法在发射端OFDM块大小、噪声与信道信息和接收端的同步信息均未知的情况下,能够实现SFBC-OFDM的有效识别,更适用于电子侦察等非协作通信场合。本文算法对时延和频偏有较强的适应性和鲁棒性,并且适用于不同的调制方式,在接收信号数充足的情况下能够获得较好的识别性能,具有优良的工程应用前景。由于本文是在仿真环境下进行的,结合算法对非协作通信场景良好的适应性,未来可进一步在4G和5G的实际环境中展开对多载波信号的实验和研究。