Mecanum 轮底盘坡道行驶的运动学研究

崔孟楠，窦志红，刘星栋，吴平

北京航天自动控制研究所，北京 100854

随着人工智能的发展，以自动导引运输车(automated guided vehicle,AGV)为代表的移动机器人产品在生产和生活领域应用获得了前所未有的发展[1−3]。Mecanum 轮由于其多自由度的特点，被广泛应用于有全向移动需求的各类型移动机器人底盘上。

Mecanum 轮 是1973 年由瑞士人Bengt Ilon 设计的，由一个轮毂支撑架和若干沿一定角度排布安装在轮毂周围自由运动的辊子组成，辊子的外表面形状是曲面，轮毂周围的辊子的轮体的包络线形成一个完整的圆。

特殊的结构使Mecanum 轮具有3 个自由度，分别为绕轮子轴线转动、绕辊子与地面接触点的转动和沿辊子轴线垂直方向的平动。由于特殊的结构及其动力特性，使得采用Mecanum 轮的底盘大多应用于较为平整的路面上，这也在一定程度上限制了该种车轮底盘的应用和推广。通过研究Mecanum 轮底盘在复杂路况下的运动特性，可以在一定程度上扩展底盘及整机的应用范围[4−5]。

1 Mecanum 轮底盘运动学及动力学分析

1.1 Mecanum 轮受力情况分析

Mecanum 轮结构如图1 所示，在平面运动时，轮毂外沿辊子的圆柱包络面与地面接触，且在任意时刻至少有一个辊子与地面接触[6−7]。

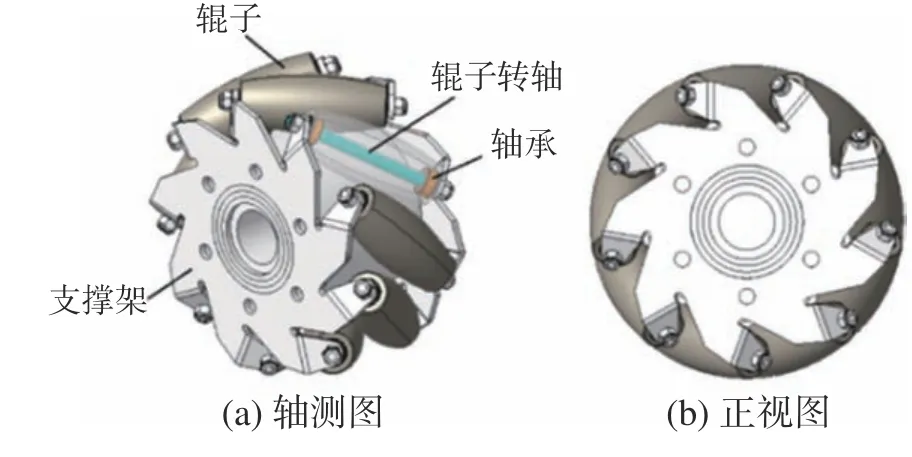
图1 Mecanum 轮结构示意

底盘行驶过程中，电机的输出扭矩Td经过离合器、减速机、传动轴、驱动桥传到车轮上，则驱动轮的扭矩T可表示为[8]

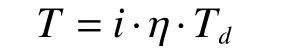
式中：i为 减速机的减速比，η为传动效率。

图2 为驱动轮滚动过程受力示意图。

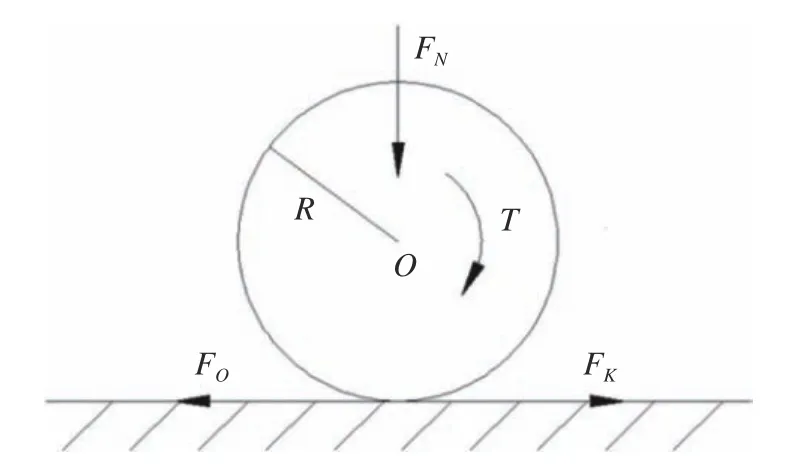
图2 驱动轮滚动过程受力示意

如图2 所示，驱动轮部位正压力为FN，轮缘与地面接触部位为静摩擦，车轮对地面产生作用力Fo，路面给车轮的反作用摩擦力即为车轮前进的驱动力Fk。工程上通过试验可以测得车轮与地面的附着系数 φ，当驱动力大于车轮对地面的附着力Fφ时会产生打滑，则车轮进行纯滚动的条件为[7−8]

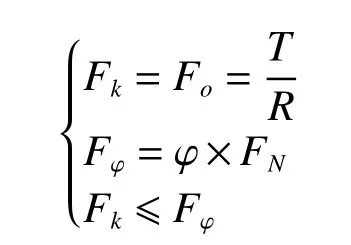
图3 为Mecanum 轮辊子受力示意图。

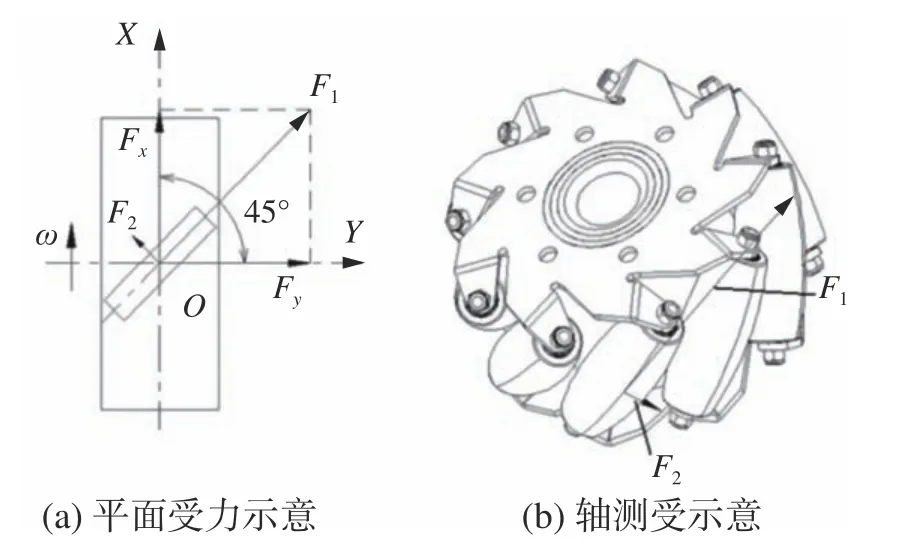
图3 Mecanum 轮辊子受力示意

如图3 所示，斜线方向为底部辊子与地面接触时的方向，辊子的倾斜角度一般为45°。牵引力Fk是 由沿辊子轴线方向上的静摩擦力F1和垂直于辊子轴线方向的滚动摩擦力F2两个力合成所得。

式中：µ1为 摩擦系数，由试验测得；µ2为滚动摩擦系数，由试验测得。

由于辊子外侧采用具有弹性且摩擦系数较大的聚氨酯、橡胶等材料制成，而辊子转轴两侧安装有滚动顺畅的轴承，因此Mecanum 轮辊子的静摩擦力F1远 大于滚动摩擦力F2，一般在分析时取牵引力Fk≈F1。在图3 所示的车轮坐标系下，牵引力Fk可 分解为Fx及Fy共2 个方向的分力，其中Fx作为车轮整体向前滚动的驱动力，根据与驱动扭矩的关系可以得到[9]：

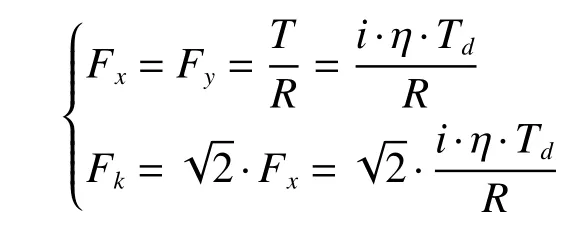
1.2 Mecanum 轮底盘运动学分析

四轮Mecanum 轮底盘是目前工业应用中最为常见的结构形式，四轮布置位置及方向在很大程度上会影响底盘整体的运动特性，综合多种运动特性分析，较为常用的一种结构布局如图4所示[10]。

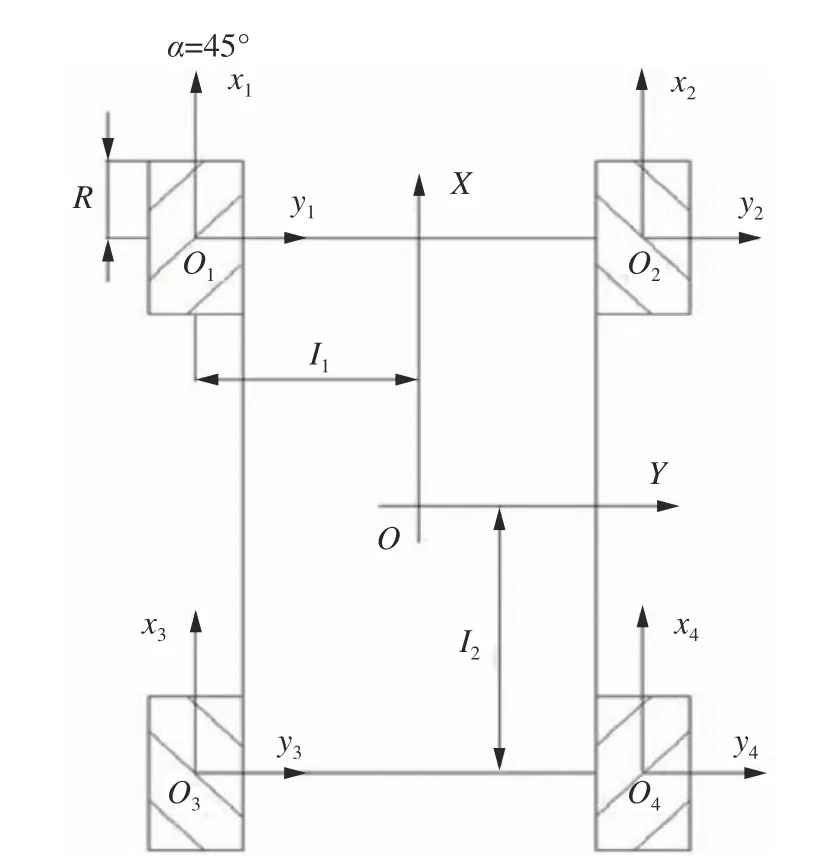
图4 四轮Mecanum 底盘广义坐标系示意

建立底盘广义坐标系XOY(图4)和单轮局部坐标系xioiyi(i=1,2,3,4)如 图5，其中R为Mecanum轮半径，I1、I2分 别为底盘轮距、轴距的一半，α为Mecanum 轮辊子轴线与轮毂轴线的夹角，4 个车轮均为45°。设4 个轮的角速度分别为 ω1～ ω4，每个轮辊子滚动速度为vg1～vg4，底盘的纵向速度为vx，横向速度为vy，旋转速度为 ωo。

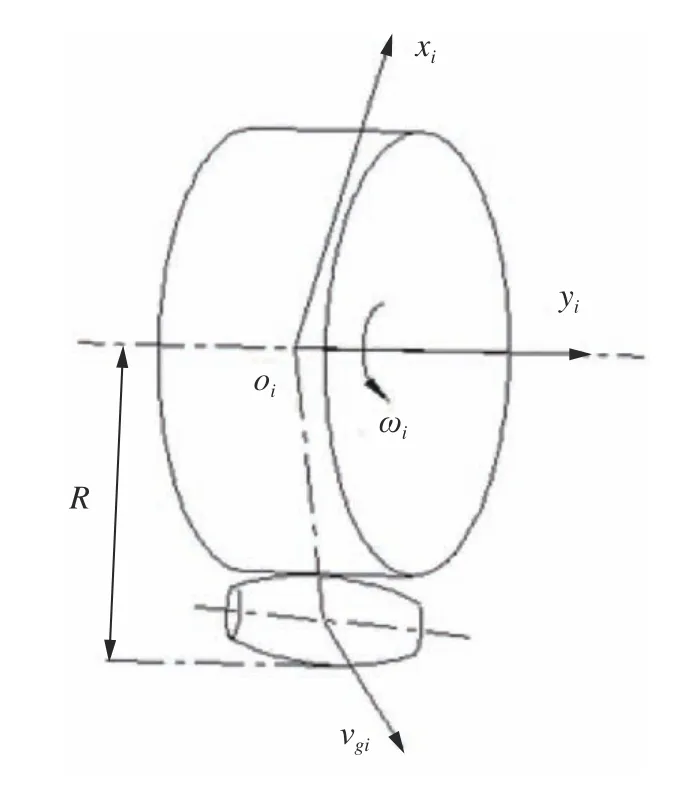
图5 单轮局部坐标系示意

将第1 个Mecanum轮在局部坐标系和整车广义坐标系中分别进行运动参数分析，其运动学方程分别如下：

在局部坐标系x1o1y1中有：

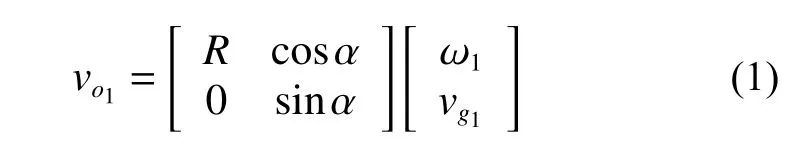
在广义坐标系XOY中有：

式(1)和式(2)联立求得：

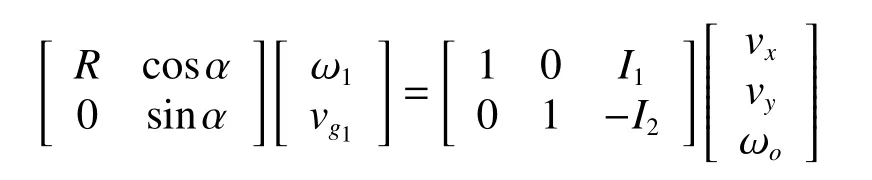
对4 个车轮进行相同的分析，则得到整车的逆运动学方程：

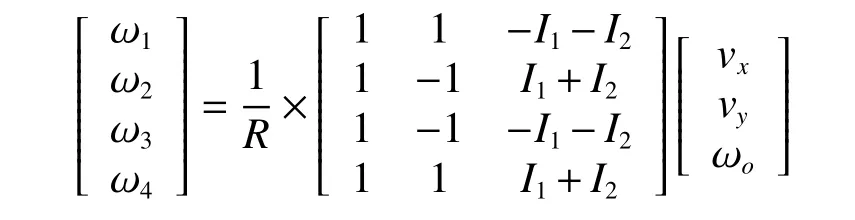
对于运动协调平稳的底盘，4 个车轮转速的线性关系为

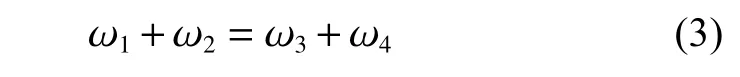
如式(3)不成立，则表明出现了底盘运动打滑现象，影响平台的正常运行。

根据底盘运动学方程可看出，通过分别控制4 个车轮的转速，车轮旋转过程中辊子与地面接触，由此产生沿辊子自身轴线方向的摩擦力，4 个车轮的摩擦力作为驱动力，通过不同组合实现底盘的各种运动模式。典型运动模式下车轮受力情况如图6。分别将4 个车轮的驱动力在底盘质心上进行合成，即可得到底盘整体的驱动合力Fk及转矩T[9−10]。

图6 底盘运动控制模式

1.3 Mecanum 轮底盘坡道静力学分析

车辆在坡道上行驶过程中，驱动轮产生驱动合力Fk,需要克服的各种阻力包括：摩擦阻力Fg、空气阻力Fw、坡道阻力Ft及 加速阻力Fa。Mecanum轮底盘在坡道上稳定低速行驶时，加速阻力Fa为0，空气阻力Fw微小可忽略，运行中的滚动摩擦阻力Fg与 由重力分量产生的坡道阻力Ft相比也较小可忽略，因此坡道行驶过程中底盘主要受坡道阻力Ft影响。

坡道阻力Ft为底盘在坡道行驶时重力沿坡道方向的分力，底盘在坡道行驶可分为直线行驶和斜向行驶2种状态。直线行驶时坡道阻力Ft=G·sinθ。斜向行驶时，如图7 所示，底盘纵向轴线与坡道纵向存在一定的偏向角δ。

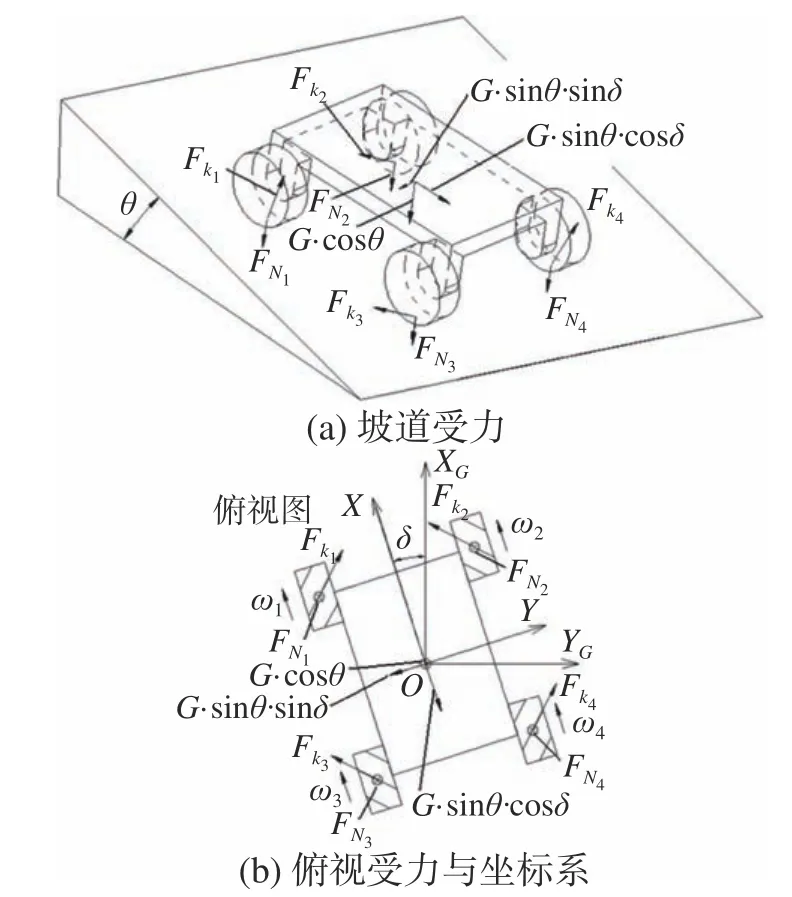
图7 斜向坡道底盘受力分解示意

由于底盘运动过程的牵引力是以摩擦力表现出来的，如果摩擦力(牵引力)小于下滑分量就会出现打滑现象。综合以上分析，底盘满足坡道上稳定行驶的工作条件为[12]

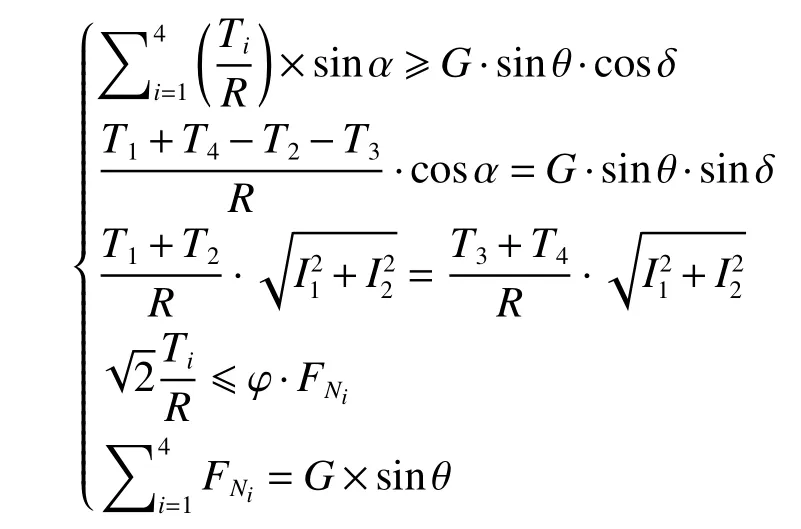
式中Ti为第i个驱动轮扭矩，i=1,2,3,4。

1.4 Mecanum 轮底盘动力学分析

图8 为底盘坡道行驶过程中坐标转换示意图，采用运动学转化方法，在广义坐标系下，定义底盘沿XG方 向的位移分量SX，沿YG方向的位移分量SY，回转角度 θO。

图8 底盘坐标转换运动简图

式中：J为底盘的转动惯量，Jω为底盘驱动轮的转动惯量，Jm为电机的转动惯量。根据静力学分析可知摩擦力在动态变化，因此需要动态控制各电机的驱动力矩，动力学分析可为底盘在斜路面上的运动平稳性控制研究提供理论依据。

1.5 坡道行驶特性分析

图9(a)为直线坡道行驶示意图，图9(b)为斜向坡道行驶示意图。在底盘上坡过程中，可分为3 个阶段：阶段1 为驶入阶段，该阶段4 个车轮先后从平面驶上坡道；阶段2 为全坡道阶段，该阶段4 个车轮与坡道完全接触；阶段3 为驶离阶段，该阶段4 个车轮先后从驶离坡道。

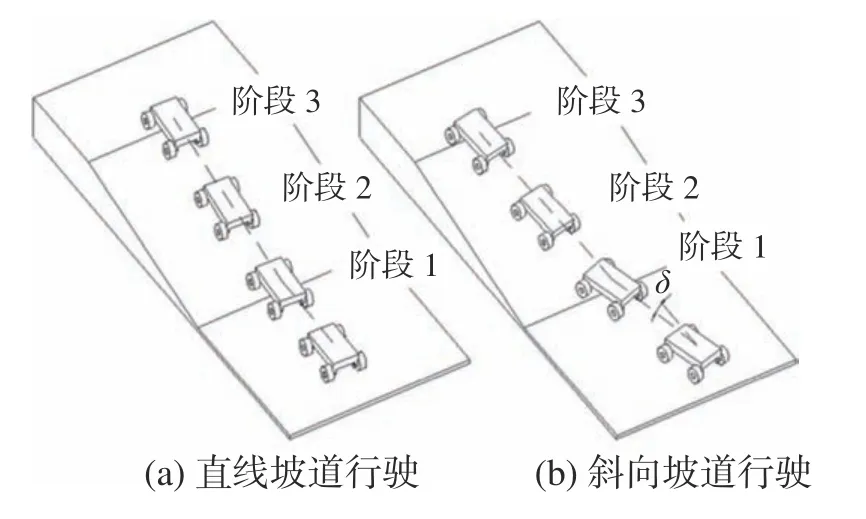
图9 底盘上坡行驶3 个阶段示意

直线坡道行驶较为简单，与水平路面直线行驶相似，只要驱动合力Fk≥Ft即可保证底盘顺利驶上坡道。

斜向坡道行驶较为复杂，在驶入阶段，由于偏向角 α的存在，4 个车轮先后与坡道接触，造成两侧车轮的对地正压力不同，受力无对称性，由此产生的驱动合力Fk及 转矩T会致使底盘出现横向滑移、方向转向等现象。驶离阶段和驶入阶段相似，而在全坡道阶段4 个车轮与地面接触良好，受力情况相对简单，运动状态较为平稳。

Mecanum 轮底盘的运动状态会受到整体结构、悬挂刚度、坡道坡度、偏移角度等诸多因素的影响，会随过程实时变化，因此无法通过简单的理论计算和分析获取准确的运行状态。本文通过对Mecanum 轮底盘斜向坡道的理论分析和运动仿真分析，提出底盘设计的优化方案，从而减小爬坡过程中底盘的横向偏移量，提高运动稳定性和对窄坡道的通过性。

2 运动仿真分析

2.1 仿真模型及系统搭建

某型机器人及底盘结构示意图如图10 所示，机器人采用四轮式Mecanum 轮底盘，前后轮采用图示的单摆臂式悬挂减震系统。在Adams 中对机器人整机进行运动学分析，仿真模型如图11 所示，由车架、Mecanum 轮、摆臂、减震器及配重等组成，定义机器人的总重为100 kg，轮距530 mm；轴距600 mm；轮半径100 mm。仿真模型对车架及悬挂部分进行了一定的简化，将配重分为前、后两块，用于模拟质心位置不同时对运动的影响；添加辊子绕自身轴的旋转副和Mecanum 轮绕轮毂的旋转副；用Impact函数模拟辊子与地面的碰撞，采用Coulomb 准则模拟辊子与地面的摩擦；在摆臂式悬挂端设置4 组弹簧阻尼器，通过设置刚度系数模拟不同的弹簧减震器。

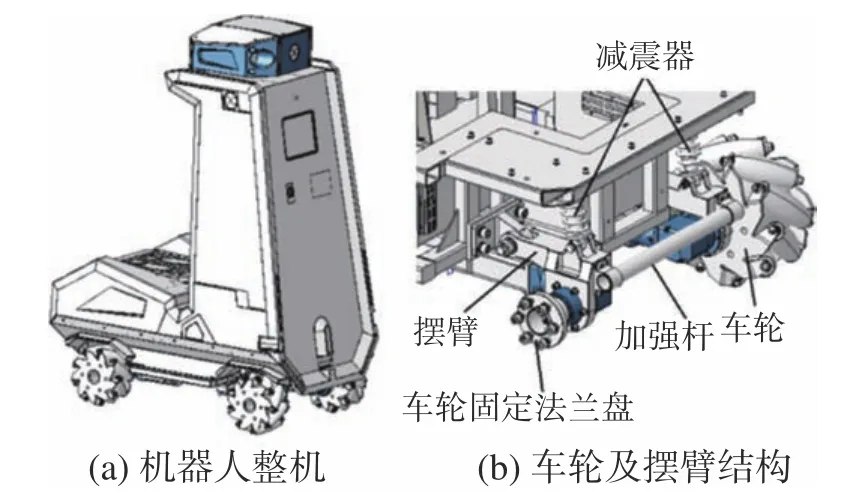
图10 某型机器人及底盘结构示意

图11 运动学仿真模型

建立4 种坡道仿真路面，分别为直线行驶上坡、斜向行驶上坡、直线行驶下坡和斜向行驶下坡。由于篇幅所限，本文仅结合相对复杂的斜向行驶上坡工况的仿真结果及其影响因素进行分析和论证。

2.2 减震弹簧刚度的影响分析

根据前文分析，斜向坡道行驶过程中车轮发生瞬时离地时会产生横向滑移，结合车体结构特点，悬挂减震的刚度系数会对离地幅度及离地时间产生影响，会直接影响运动过程的偏移量。

仿真工况为未加载配重质心居中的状态，坡道倾角为5°、10°和15°，底盘采用直线运动控制模式，4 个车轮的转速均为460 °/s，驶入坡道时的偏向角为10°，仿真时间6 s。

图12 为弹簧刚度系数k=800 N/mm 时底盘在10°倾角坡道上的运动情况，从图中可以看出与1.5 节中的分析一致，底盘在驶入及驶离坡道过程中个别车轮会出现瞬时离地现象，产生沿Y方向的横向驱动力及由于驱动力不平衡产生的车体扭转，由此造成在这2 个阶段发生明显的横向滑移。在全坡道行驶阶段，由于4 车车轮与地面接触良好，运行状态较为稳定，未发现明显的偏移。

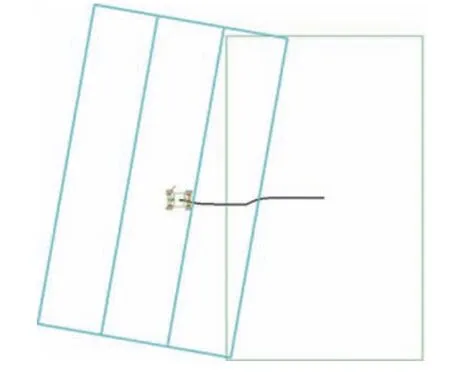
图12 斜向坡道行驶轨迹示意(k=800 N/mm)

图13 为设置不同减震刚度后，底盘在3 种倾角坡道上的偏移量曲线。

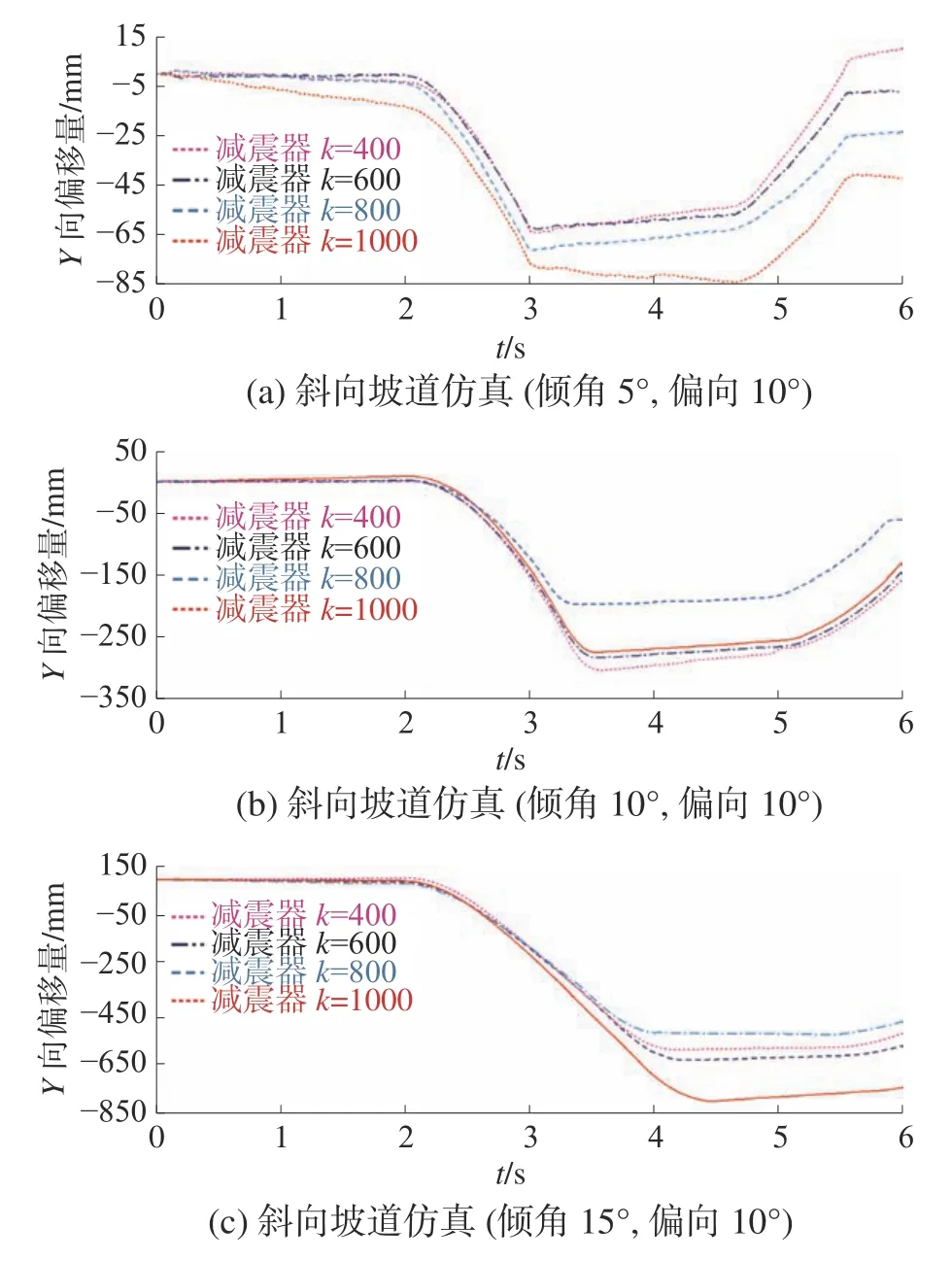
图13 不同刚度系数横向偏移量曲线

通过表1 可以看出，当刚度参数相同时，随着坡道倾角的加大偏移量会随之增大。在倾角5°的坡道上，偏移量呈现随刚度线性变化的趋势，但在10°和15°坡道上却不存在该规律，偏移量较小的反而是刚度较大的两种状体。因此在较大倾角坡道上需要注意选择1 个合适的刚度系数才有利于减小最大偏移量。

表1 不同刚度系数横向偏移量数据表 mm

2.3 质心位置的影响

根据前文的分析，增加驱动轮部位的正压力可以有效提高车轮的附着力Fφ，减少车轮空转，提升底盘对牵引力的利用，从而提高运动的稳定性。因此通过调整质心位置，理论上可以减小坡道运行时的偏移量。

以2.2 中3 种坡道最大偏移状态为基线，保证整体重量不变，通过调整前、后配重的方式将质心位置前移、后移80 mm。图14 为弹簧刚度系数为k=1 000 N/mm，质心向后调整80 mm 的底盘在10 °倾角坡道上的运动情况。

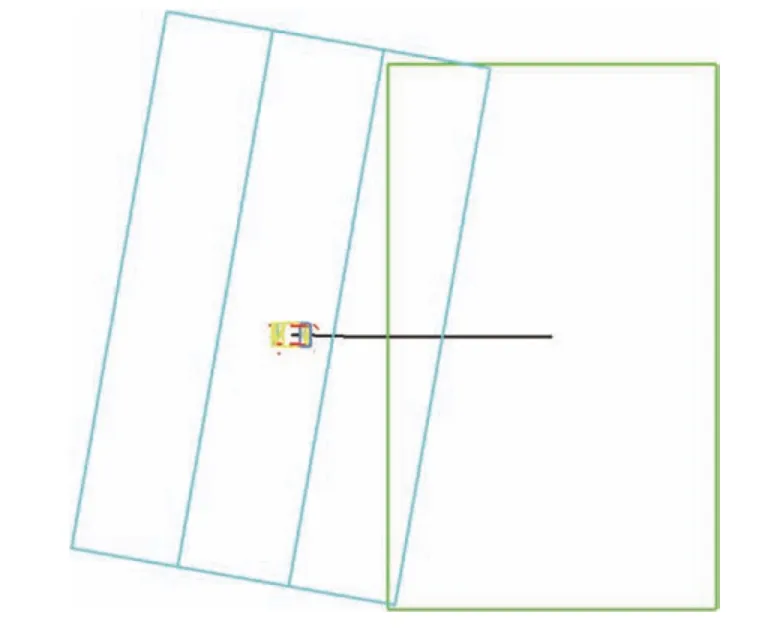
图14 斜向坡道行驶轨迹示意(质心靠后状态)

图15 为底盘在3 种倾角坡道上的偏移量曲线。

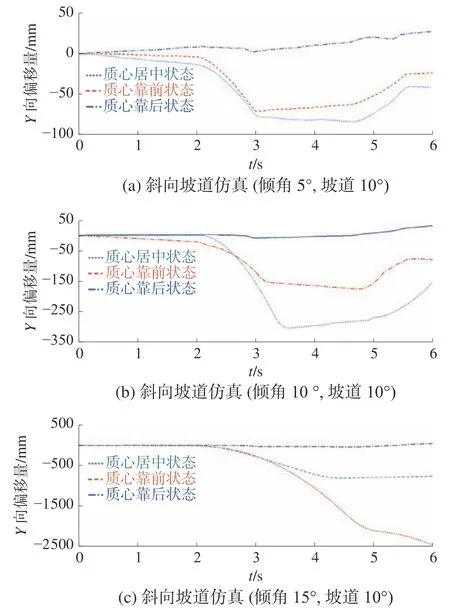
图15 不同质心位置横向偏移量曲线

从表2 中数据可以看出：质心前移后，在5°及10°倾角坡道上，均能减小一定的横向偏移，但在15°坡道时却出现较为严重的侧滑而无法完成爬坡动作。与之不同的是质心后移状态的底盘，侧向偏移量明显减低。因此对于本文分析中所采用的“O 型布局”麦克纳姆轮底盘，质心后移更有利于提高坡道行驶过程中的运动稳定性，提升底盘的爬坡能力。

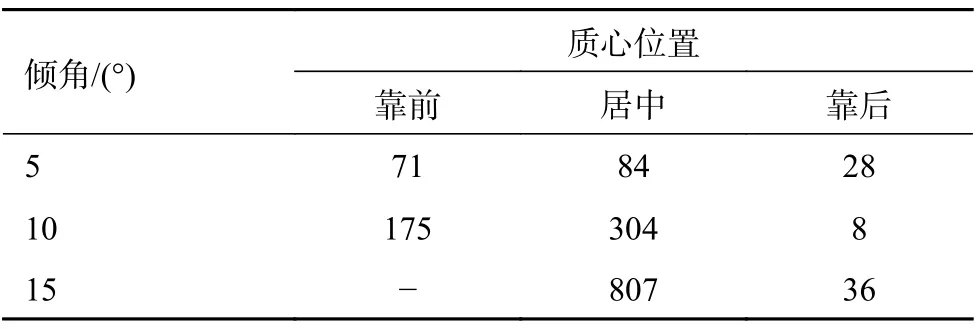
表2 不同质心位置横向偏移量数据表 mm

2.4 偏向角的影响分析

根据前文的分析，当偏向角增大时横向坡道阻力Fty也相应增大，也会对运动过程中的横向偏移产生影响。以2.2 节中3 种坡道最大偏移状态为基线，将偏向角从10°增大至15°。横向偏移曲线如图16 所示。

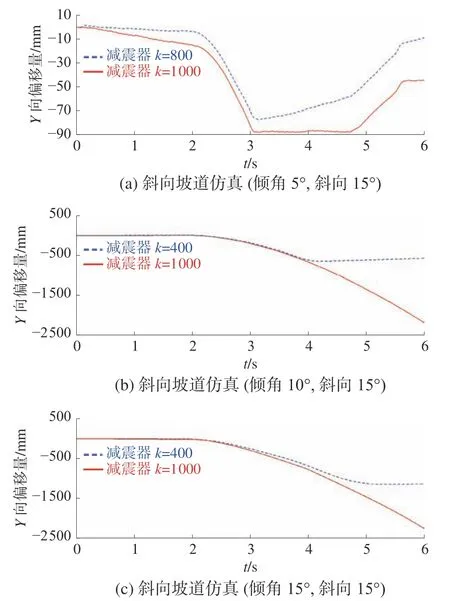
图16 15°偏向角横向偏移量曲线

从表3 中数据可以看出：偏向角增大后，横向偏移量也会随之增大，其中在2 种工况下出现较为严重的侧滑，如图17 所示，底盘无法爬坡。因此增大偏向角及选择不合适的减震器会影响底盘的爬坡能力。

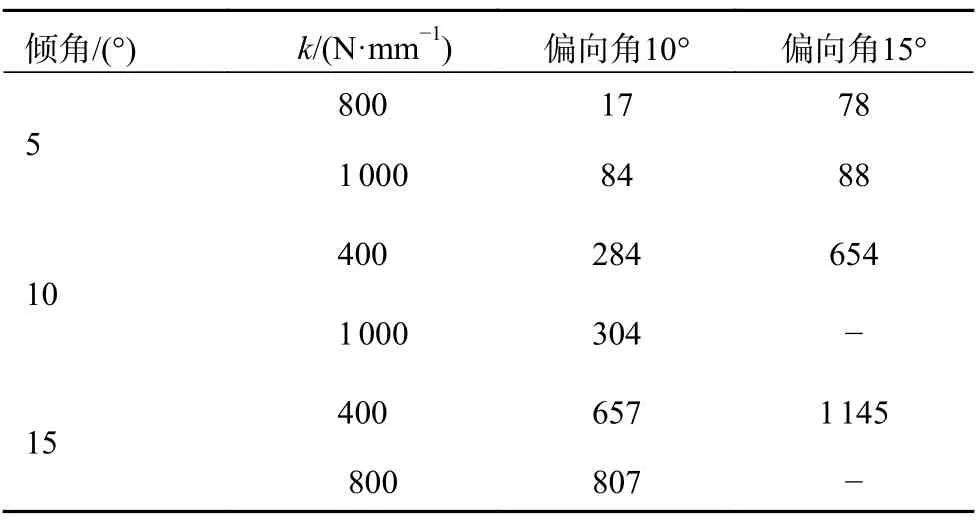
表3 不同偏向角横向偏移量数据表 mm

图17 斜向坡道行驶轨迹示意(严重横向侧滑状态)

3 实物验证试验

采用某型机器人实物进行了实际路况下的斜向坡道行驶测试，坡道角度约10°，分别进行偏向角为10°和45°两种情况进行试验，提取机器人差分GPS 轨迹数据，并与前文仿真数据进行比对。图18、19 为10°偏向角机器人样机试验图和采集的位置曲线图，样机爬坡过程中运行较为平稳，未出现明显的滑移，实物试验位置曲线与仿真分析的曲线基本吻合；图20、21 为45°偏向角机器人样机试验图和采集的位置曲线图，样机在驶入坡道阶段发生了较为明显的侧向滑移，未能完成爬坡动作，与仿真分析的结果基本一致。由于条件所限现场坡道并非标准角度坡道，在坡度、偏向角、地面平整度等方面与仿真的标准坡道存在一定差异，但通过试验中实物的运行轨迹及变化规律可以看出，实物试验和仿真分析的情况相吻合，验证了前文理论分析的正确性。

图18 10°偏向角坡道行驶试验

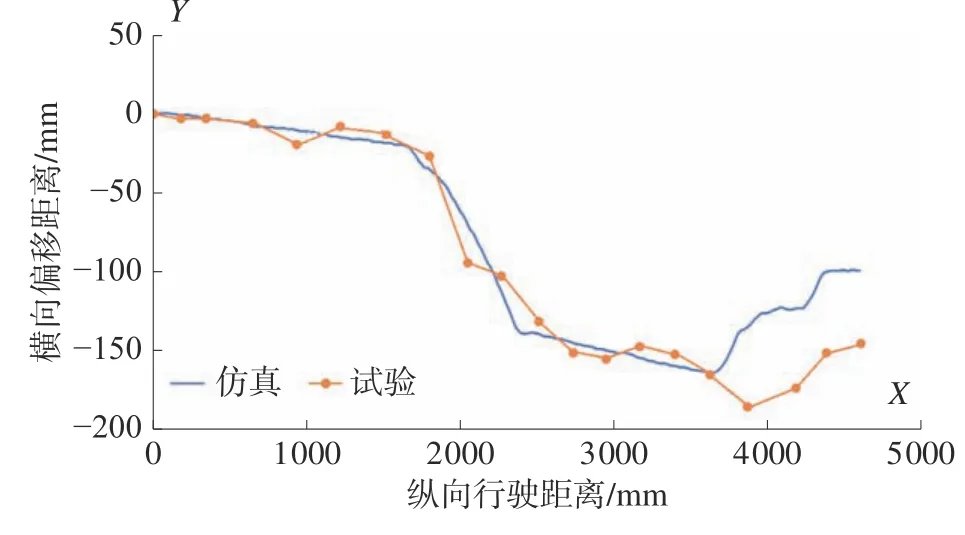
图19 10°偏向角坡道行驶位置曲线对比

图20 45°偏向角坡道行驶试验

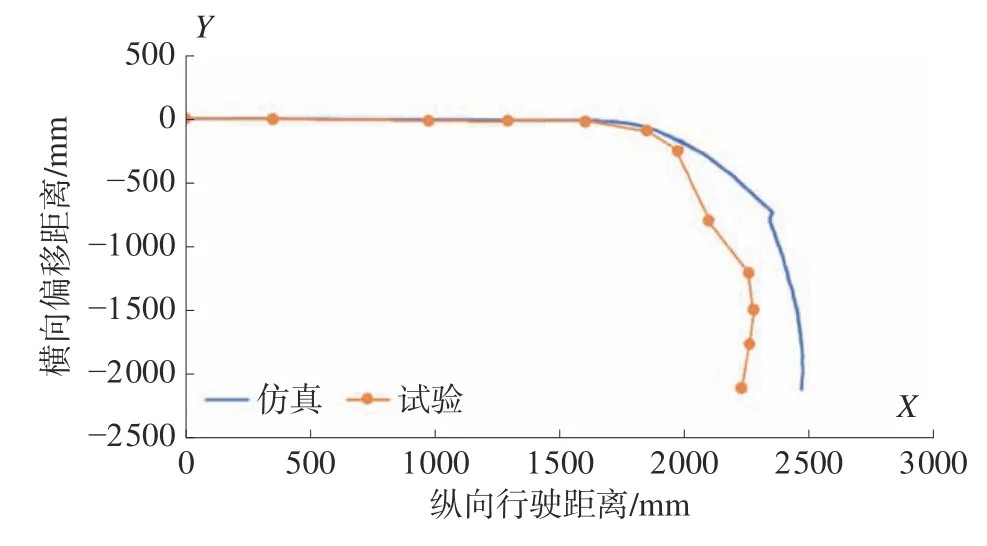
图21 45 °偏向角坡道行驶位置曲线对比

4 结论

通过仿真分析和实物试验测试可以看出，Mecanum 轮底盘在斜向坡道行驶中，尤其是大偏向角状态下确实存在滑移现象。在一定偏向角范围内，通过优化减震悬挂、调整质心位置等方式，能够使其较为平稳地进行斜向坡道行驶。后续进一步结合运动控制算法优化，例如通过加装IMU检测底盘方位状态并实时调整运动控制模式对运动偏移的趋势进行修正，相信将进一步提升Mecanum 轮底盘对复杂路况下的适应能力。