基于CAESES 的船用螺旋桨三维建模研究
2021-11-29王超吴浩韩康赵雷明
王超,吴浩,韩康,赵雷明
哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
螺旋桨作为船舶领域中应用最广泛的推进器,其设计效率及建模精度直接影响着船舶的快速性、经济性与安全性。随着对螺旋桨高效、快速建模要求的提高,传统几何建模方法被先进的三维建模技术所取代,目前,应用较为广泛的软件包括Solidworks[1−2]、AutoCAD、CATIA[3]、ProE[4]和UG[5−8]等。
螺旋桨型表面十分复杂,具有变化的叶切面、螺距角、弦长等几何特性,螺旋桨三维建模的关键在通过空间坐标将复杂的桨叶型值进行表达,再选用合适的样条曲线、曲面进行拟合。而CAESES 作为一款主要应用于产品设计前期的参数化建模及优化设计软件,具有强大的三维参数化建模、耦合仿真、优化设计等功能,内部提供了丰富的点、线、面操作命令,可通过调整相应的控制参数实现曲线、曲面的平滑过渡,保证模型的光顺。目前被广泛应用于船舶[9−10]、航天、汽车[11]等领域产品的设计及性能优化工作中。
本文基于Fortran 编程语言,实现了输入桨叶参数得到桨叶表面网格点空间坐标;再通过Excel 进行数据的二次处理得到了CAESES 输入文件;最后导入feature,执行相应的操作快速生成了螺旋桨三维实体。针对不同种类螺旋桨,只需更改程序的输入文件即可,该方法简化了螺旋桨三维建模设计过程,规避了通用软件操作复杂的弊端,有效提高了螺旋桨的设计精度。
1 螺旋桨模型
螺旋桨主要由叶片和桨毂两部分组成。通常情况下,水面船舶螺旋桨桨叶有3~6 片,由于其特殊的几何外形无法用特定函数来表达曲面结构,因此常选用叶剖面的位置参数和其他类型的特征数据进行表示,螺旋桨的参数化变量包括螺距、纵倾、侧斜、弦长、厚度和拱度,这6 种类型的数据构成了螺旋桨建模的参变量体系[12]。
程序中,将螺旋桨固定于如图1 中的坐标系o−xyz中,原点o位于桨盘面的中心点,x轴沿桨毂轴线方向指向下游,y轴沿螺旋桨某一叶片的母线方向,z轴与x轴和y轴组成右手坐标系。

图1 螺旋桨坐标系
同时采用一柱坐标系o−xrθ作为参考坐标系,θ 的方向由y轴起始按逆时针方向旋转。在柱坐标系下,如图2 所示,用s表示叶剖面上的点到导边的弦向距离,c1表示叶剖面上导边至母线的距 离,xr表示叶剖面处的纵倾,θs表示剖面的侧斜角,yb、yf分别表示叶背、叶面上的点到弦线的距离。

图2 螺旋桨柱坐标系
则螺旋桨半径为r处的叶剖面上的点的坐标可表示为
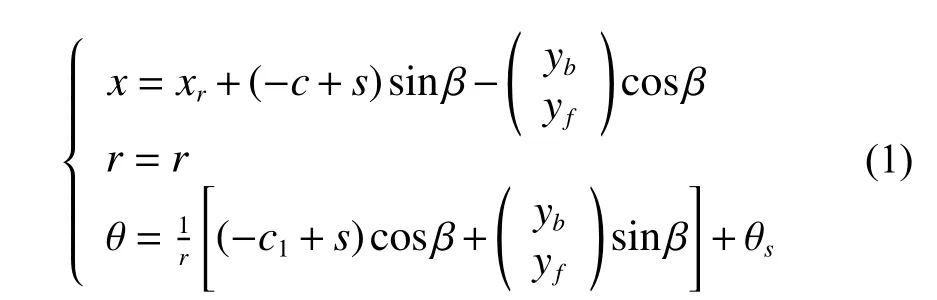
柱坐标系与直角坐标系之间的转换关系符合式(2):
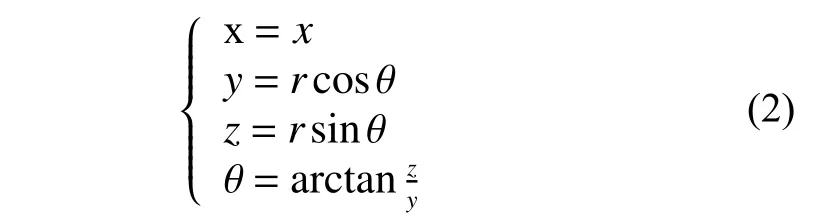
因此,式(1)在坐标系o−xyz下的相应坐标为

2 螺旋桨空间坐标
本文螺旋桨空间坐标利用Fortran 语言进行编程,程序流程如图3 所示。

图3 空间坐标程序流程
以KP505 桨为研究对象,进行螺旋桨实体三维建模,主要螺旋桨参数如表1 所示。

表1 KP505 主要参数
具体建模步骤如下:
1)以txt 文本格式输入螺旋桨的几何参数,部分数据如图4 所示。

图4 螺旋桨几何参数
2)计算螺旋桨剖面面积、体积矩、惯性矩等宏观参数,部分程序如下:

3)计算螺旋桨几何参数,规范参数单位。部分程序如下:

4)网格划分,生成网格节点空间坐标,将数据输出,部分程序如下:

5)输出螺旋桨AutoCAD 图形,如图5 所示,观察桨叶网格的连续性,导边、随边坐标数据的封闭性以及螺旋桨的几何特征,以检验生成模型的正确性。

图5 AutoCAD 中KP505 桨模型
3 CAESES 中螺旋桨三维实体建模
由于生成的螺旋桨空间坐标txt 文件不符合CAESES 的输入文件格式,因此需将输出数据进行后处理,在此选用Excel 将空间坐标转换成如下形式:

本例中所设置的螺旋桨弦向、径向网格划分数目均为16,网格划分形式均采用半余弦分割,因此,共产生网格节点2 890 个,单个桨叶不同半径处叶背叶面均由17 个点通过插值曲线得到,处理后的数据可直接应用于CAESES 软件。
具体CAESES 中建立螺旋桨三维模型的过程如下:
1)导入Feature。Feature>New Definnition>General,Type Name 中输入KP505>Greate Function,输入二次处理后的数据>Apply>Close。
2)执 行Feature。Feature Definnition>KP505>Execute Definnition,命名为point_line>Execute。
3)建立单桨叶曲面。CAD>Scope,命名为blade>子空间内根据已生成的空间曲线执行LoftedSurface(介于两条或者多条任意曲线之间的曲面)和RuledSurface(介于两条任意曲线之间的直线曲面)命令生成s1、s2、s3,分别为螺旋桨压力面、吸力面、叶梢面。
4)运用Brep(主要用于曲面模型之间的布尔运算)命令建立单桨叶实体。CAD>Breps>Brep,将s1、s2、s3添加到Sources 中,重命名为single_propeller。
5) 运用Brep 命令建立完整桨叶实体。CAD>Breps>More>Periodic Brep,其中Geometry 中选择single_propeller,N=5,Rotation Axis 选择X轴,重命名为propeller_all,注意在运用Brep 命令过程中螺旋桨局部可能会产生变形,此时只需要稍微调小全局公差即可。
6)桨毂实体。与螺旋桨建模方法类似,这里不再赘述。
7)生成螺旋桨三维实体模型。CAD>Breps>Brep,命 名为Propeller 将propeller_all 和hub 添加到Source 中生成完整螺旋桨模型,如图6 所示。

图6 KP505 桨实体三维模型
4 螺旋桨水动力性能验证
为进一步验证建模方法的准确性,采用CFD方法对模型进行敞水性能计算,计算结果与试验数据做对比[13−14]。
本次计算参照的是2015 年东京船舶流体力学CFD 研讨会所提供的数据[15],螺旋桨转速n=9.5 r/s,水的密度、运动黏度分为 ρ=999.1 kg/m3、υ=1.139×10−6m2/s。
计算域具体尺寸如图7 所示。在网格划分上,静止域选用切割体网格,旋转域选用切割体网格,边界层处采用棱柱层网格,棱柱层层数为8,棱柱层延伸取1.3,桨叶近壁面第一层网格无因次化厚度y+≤1。基础尺寸均取0.125 m,为提高计算精度,对桨毂、叶梢和桨后处进行局部加密,根据建立的计算域方向,设置速度进口、压力出口和对称平面,静止域与旋转域之间设置交界面,并禁用棱柱层网格,最终旋转域网格数约为365.8×104,静止域网格约为236.6×104,总网格数约为602.4×104,整个计算域的网格如图8 所示。

图7 计算域尺寸

图8 体网格
设置物理模型,其中湍流模型选用K-Omega湍流,采用旋转参考坐标系法,旋转速率为9.5 r/s,保持螺旋桨转速不变,通过改变进速VA求解不同进速系数下的推力系数、扭矩系数、效率,分别计算进速系数为0.2、0.4、0.5、0.7 和0.8 时的KT、10KQ、η0,敞水特性曲线如图9 所示。

图9 敞水特性曲线
仿真值与实验值对比如表2 所示。

表2 敞水特性对比
由表2 可知,推力系数、扭矩系数和效率的误差均小于5%,在误差允许范围内,因此,本文提出的基于CAESES 的建模方法是有效可行的。
5 结论
本文以Fortran 编程语言为主体,基于CAESES软件提出了一种螺旋桨建模方法。通过编程实现了螺旋桨桨叶参数到三维空间坐标的转换,后处理网格点坐标得到了符合CAESES 建模的输入文件,在CAESES 界面执行相应命令得到了螺旋桨实体模型,最后结合数值仿真,与试验结果作对比验证了建模方法的准确性。在建立不同的螺旋桨模型时,只需更改程序的输入文件即可,大大缩短了建模时间,提高了螺旋桨的生成效率。
