装配式浆锚连接有限元计算弹簧-杆模型研究
2021-11-29周文君李姗珊
周文君,吴 敏,李姗珊,张 帅
(1.吉林建筑科技学院 土木工程系,长春 130114;2.中国市政工程东北设计研究总院有限公司,长春 130021)
装配式混凝土建筑是部分构件或全部构件工厂内生产、施工现场进行拼装的建筑形式,因此该技术具有高效推动建筑产业化、工业化发展,减少物料损耗、节约施工成本、减少对环境影响等优点。
钢筋浆锚搭接是实现预制构件连接的主要形式之一,在装配式混凝土结构新技术研发中备受关注。陈云刚等[1]进行足尺的现浇式与装配式剪力墙试件低周反复荷载试验,得到装配式混凝土剪力墙试件初期刚度有所下降;外墙试件水平拼缝上移后,承载力会有所提升的结论。武守晗[2]结合插入式预留孔灌浆钢筋搭接连接技术和全预制装配整体式剪力墙结构预埋金属波纹管搭接连接技术,对现有的约束浆锚钢筋搭接连接技术予以改进,提出插入式螺旋箍筋波纹管浆锚连接技术。吴东岳等[3]对一浆锚连接装配式剪力墙空间结构模型进行低周反复加载试验,试验表明浆锚连接在搭接区边缘存在新薄弱面。
有限元计算是推动装配式混凝土结构技术进步的主要手段。张壮南等[4]在进行装配式剪力墙浆锚连接的受力性能试验研究中,应用ABAQUS分析,得出在满足锚固需求条件下,增加后浇宽度可提高墙体的受剪承载力、减少凹槽对墙体受剪承载力影响较小的结论。石棚等[5]基于ANSYS完成了钢筋插入式波纹管浆锚连接受力性能研究,分析得出了不同钢筋锚固长度下,接头破坏对应的不同形态。但通过查阅大量文献发现,在应用有限元计算研究浆锚连接装配式混凝土结构技术的文章里,处理浆锚连接问题时,几乎没有涉及引用可靠理论指导浆锚连接有限元建模的论述[6-10]。标准化浆锚连接节点建模工艺是确保利用有限元理论计算浆锚连接装配式结构时得到可信结果的必经之路,因此,本文通过理论推导的方法提出“弹簧-杆”模型模拟浆锚连接,并通过仿真计算验证模型。
1 模型描述
1.1 浆锚连接
浆锚连接是在预制混凝土构件内预留孔,将外伸一定长度的钢筋插入对应位置的预留孔道里,钢筋与孔道内壁之间注入无收缩、高强度水泥基料实现连接,如图1所示。预制钢筋混凝土构件采用预留孔道后灌注砂浆的浆锚连接,砂浆是在钢筋搭接完成后再灌注并养护硬化。
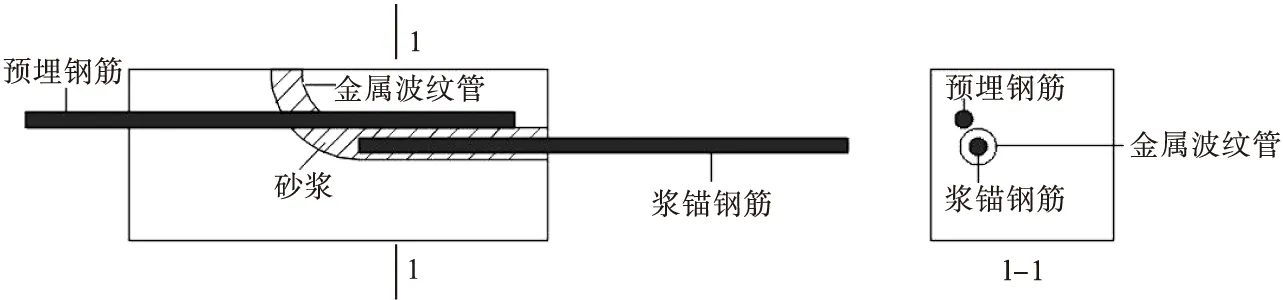
图1 浆锚连接构造
1.2 后注砂浆内力状态分析
预制构件浆锚连接节点通常处在如图2的弯矩M、轴力N及剪力V(横向水平力)作用下。

图2 浆锚连接垂直钢筋搭接方向的受力情况
用垂直于纸面且平行于OY方向的面1截开浆锚连接节点,在轴力N与弯矩M作用下,砂浆在该截面出现正应力σm,经推导正应力为
(1)
式中:σm为截面正应力;αE1为预制构件外伸钢筋弹性模量与砂浆弹性模量比值;As1为预制构件外伸钢筋截面面积;αE2为所接构件纵筋弹性模量与砂浆弹性模量比值;As2为所接构件纵筋截面面积;αE3为混凝土弹性模量与砂浆弹性模量比值;As3为混凝土截面面积;Am为砂浆截面面积;Im0为参照砂浆弹性模量计算的换算截面惯性矩;y0为参照砂浆弹性模量计算的换算截面重心至砂浆位置距离。σm足够大时砂浆单元会被拉断。
在横向剪力V作用下,后注砂浆承受剪压(拉)应力,砂浆在该截面出现OY向的剪压(拉)应力为
(2)
式中:τm1为砂浆剪(拉)应力;S0为剪力计算点以上或以下部分对参照砂浆弹性模量计算的换算截面型心轴净距;b为剪应力计算点的截面宽度。τm1足够大时砂浆单元会被剪碎。
在轴力N作用下,预制构件外伸纵筋与后注砂浆产生相反运动趋势,接触界面出现剪切应力τm2,钢筋受力情况如图3所示。
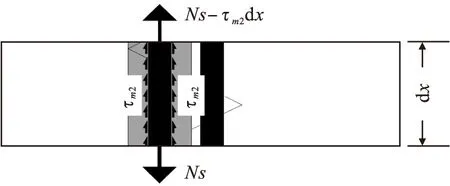
图3 浆锚连接平行钢筋搭接方向的钢筋受力情况
后注砂浆与混凝土接触面也产生相反运动趋势,接触界面出现剪切应力τm3,砂浆受力情况如图4所示。
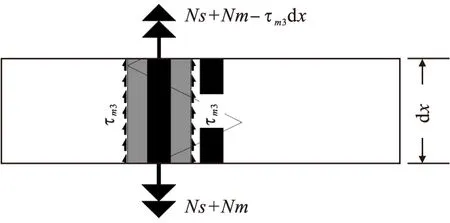
图4 浆锚连接平行钢筋搭接方向的砂浆受力情况
当τm2、τm3足够大,后注砂浆边界将会在垂直于纸面且平行于OX轴向形成剪切面,导致砂浆粘结作用破坏,砂浆与钢筋、混凝土表面脱离,严重时,外伸钢筋发生拔出破坏。
1.3 弹簧-杆-块单元模型
从上述分析看出,后注砂浆单元需要承受平行于OX轴向的正应力,此应力通过砂浆与混凝土及钢筋间的粘结作用传递应力;承受平行于OY轴向的剪压应力,此应力通过砂浆与混凝土及钢筋间的挤压作用传递应力;后注砂浆与混凝土及外伸钢筋接触面由于反向运动趋势存在,会导致粘结力破坏。因此,假定浆锚连接节点有限元模型由块体单元、杆单元及弹簧单元构成,其中混凝土块体单元、钢筋杆单元与砂浆块体单元间通过杆单元传递OY轴向的剪压(拉)应力;通过弹簧单元传递平行于OX轴向的剪切应力;杆单元和弹簧单元组成的“类桁架体系”与砂浆单元共同承受截面正应力。随着杆单元的失效,弹簧单元能较合理地反馈砂浆块体单元、混凝土块体单元及外伸钢筋块体单元间的反向运动。弹簧-杆-块单元模型如图5所示。

图5 弹簧-杆-块单元模型
1.4 弹簧-杆模型
浆锚连接多用在剪力墙-剪力墙、剪力墙-梁、柱-柱、柱-梁间连接中。在研究装配式剪力墙抗震方面,剪力墙往往分为上下片,如装配式剪力墙-连梁结构等;这样的剪力墙体系进行有限元分析时,浆锚连接采用“弹簧-杆-块体单元”模型建立相当复杂,因此简化“弹簧-杆-块体单元”模型为“弹簧-杆”模型,如图6所示。
“弹簧-杆”模型忽略掉代表砂浆的块体单元,砂浆力学影响由弹簧-杆形成“类桁架体系”取代。“类桁架体系”与桁架不同,桁架中一部分杆单元由刚度较大弹簧单元代替,形成一个有一定变形能力的传力模型,能较为合理地替代块体砂浆单元。组成桁架的弹簧使传力模型表现出允许钢筋与混凝土产生一定相对运动功能,模拟浆锚连接发生强度破坏时钢筋与混凝土的滑移脱离现象;变形至杆单元平面外失稳后,桁架体系破坏,即砂浆与波纹管节点粘结破坏,代表砂浆的桁架体系会绕孔道内钢筋一定程度转动。
1.5 弹簧-杆-块单元模型简化弹簧-杆模型可行性验证
取一浆锚连接节点,采用弹簧-杆模型与弹簧-杆-块单元模型分别建模计算(两种模型选取的弹簧单元与杆单元力学参数与几何参数不同),其加载速率与边界条件相同,通过调整弹簧单元与杆单元相关参数,可控制两模型均在t=31.78s时刻发生极限破坏。节点破坏时应力云图见图7所示。观察图7发现该浆锚节点在两种模型建模下计算,其破坏时状态几乎相同,其埋藏在混凝土内钢筋未屈服,剪切面处混凝土变形明显,其埋藏在砂浆内钢筋在端部少量拔出,最终该钢筋达到极限强度,浆锚节点破坏。
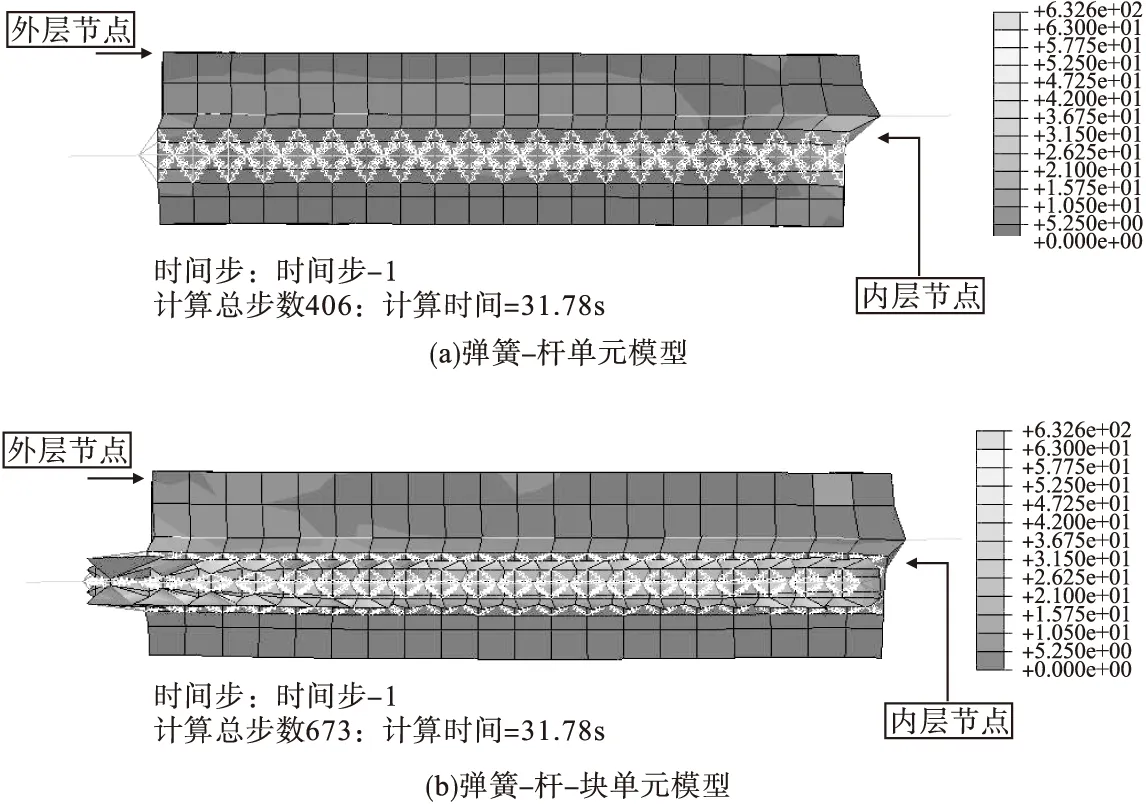
图7 节点破坏时刻(t=31.78s)应力云图
获取外层节点与内层节点的平均位移随时间变化数据,绘制节点平均位移-时间曲线,见图8所示。
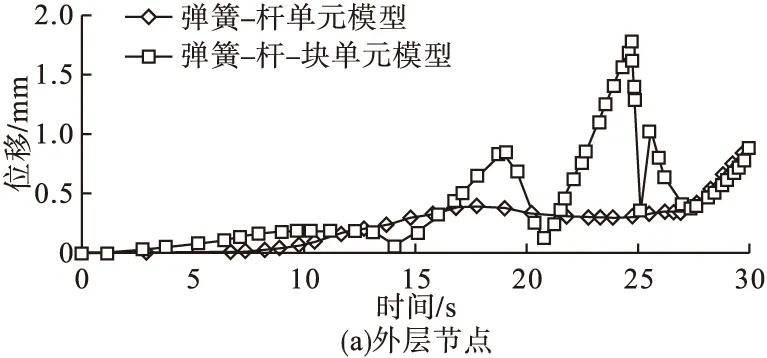
图8 节点平均位移-时间曲线
加载过程中弹簧-杆-块单元模型建立的浆锚节点在部分砂浆单元粘结力破坏后,砂浆与波纹管内壁脱离,在两根钢筋间剪切力作用下,砂浆围绕孔道内钢筋转动,与波纹管内壁产生摩擦,使浆锚节点剧烈振动,因此其位移曲线围绕弹簧-杆单元模型建立的浆锚节点位移曲线波动(弹簧-杆单元模型浆锚节点不存在振动),加载终止时振动也随之停止,在接近破坏时两曲线位移值逐渐收敛到同一数值。
结合两种建模形式下浆锚节点应力云图分布与节点平均位移曲线比较,说明将弹簧-杆-块单元模型简化成弹簧-杆单元模型可行。
2 弹簧-杆模型验证
2.1 计算模型
2.1.1 构造及材料

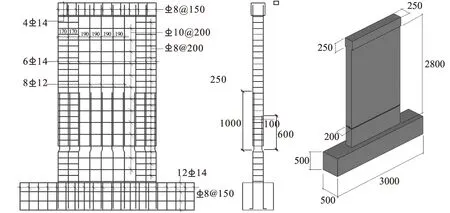
图9 剪力墙构造及尺寸(单位:mm)
构件采用HRB335级钢筋直径8mm、10mm、12mm、14mm,参数见表1所示。

表1 钢筋材料参数
文献[1]并未介绍试验使用的混凝土类别,但对比不同组别的混凝土试件试算得到的滞回曲线不难发现,试验应采用C45级混凝土,参数见表2所示[11-15]。

表2 混凝土材料参数
拼接缝处采用外高内低的Z形拼缝,拼缝处填充弹性密封胶。密封胶材料模型参数选自文献[16]中的Reduced Polynomial材料模型参数替代,见表3所示。

表3 弹性胶粘材料参数
2.1.2 有限元模型处理
有限元模型应用ABAQUS隐式计算:混凝土网格C3D8R单元,单元数量26182个;模型钢筋网格C3D8R单元,单元数量9072个;模型浆锚连接杆T3D2单元,单元数量1361个;模型浆锚连接弹簧DASHPOTA单元,单元数量2859个。网格为六面体,边长为40mm,浆锚连接有限元处理如图10所示。
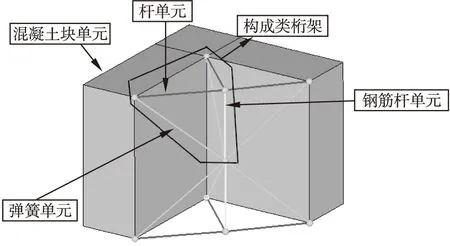
图10 浆锚连接有限元处理
2.1.3 模型加载
在初始分析步,约束地梁两端部,防止模型出现水平位移。在一阶段分析步,在剪力墙顶梁几何中心位置,沿竖直施加轴压力,轴压比控制为0.10,同时约束剪力墙平面外转动及平面外移动。
在二阶段分析步,水平荷载采用力和位移混合控制加载模型,其中力加载阶段参照文献[1]将力值折算成位移,加载曲线见图11所示。

图11 时间-位移加载曲线
加载初期试件处于弹性受力状态;荷载加载到181kN时,拼缝处部分混凝土出现损伤,逐渐形成水平贯通;当荷载达到321kN时,边缘构件拼缝处竖直分布钢筋屈服,试件进入屈服阶段。钢筋应力云图如图12所示。
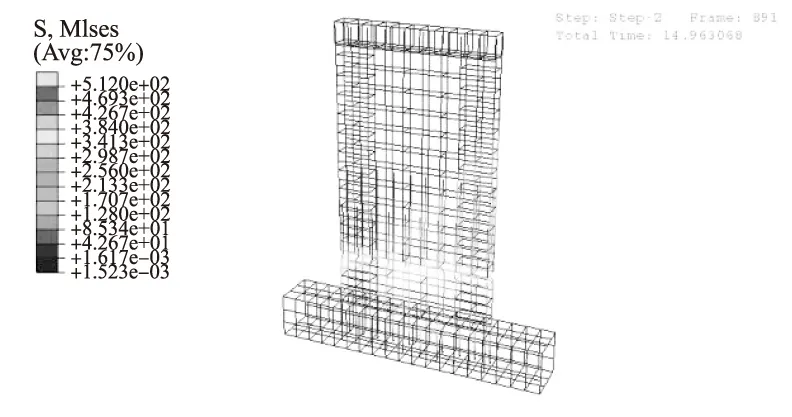
图12 钢筋应力云图
加载进入水平位移控制阶段,水平位移增至四倍屈服位移52mm时,水平力达596kN,对52mm级水平位移施加第二次循环荷载,水平裂缝两端混凝土压溃,计算终止。
以上是对有限元模拟结果的描述,对比文献[1]试验研究,试验初期试件未开裂,处于弹性阶段;荷载加至170kN剪力墙水平拼接处出现裂缝,荷载350kN时,边缘构件拼接缝处竖直分布钢筋屈服,试件进入屈服阶段,屈服位移13mm,试验转为位移控制阶段。水平位移至四倍屈服位移,即52mm时,水平力达到最大值613kN,对52mm级水平位移施加第二次循环时,水平缝两端混凝土压溃,出现大面积剥落,钢筋裸漏,试验终止,发现试验与模拟各阶段受力情况基本吻合,计算结果与试验对比见图13所示,试验图片引自文献[1]图7b。

图13 混凝土损伤云图
2.2 计算结果对比分析
2.2.1 滞回曲线对比
模拟得到滞回曲线如图14所示,对比文献[1]图8b滞回曲线发现,加载前22s试验滞回曲线峰值力几乎一致,滞回曲线卸载刚度与试验一致;但在加载22s至模拟结束,滞回曲线的峰值力略低于试验,该点与试验结果不一致,但此问题与“弹簧-杆”模型关系不大,在其他文献的模拟与试验的对比中也会出现,其主要原因是模拟中钢筋与混凝土间的粘结-滑移效应采用加速钢筋材料峰值应力衰减速率的方法等效,这种等效一定程度上造成模拟得到的滞回曲线在后期峰值力低于试验。
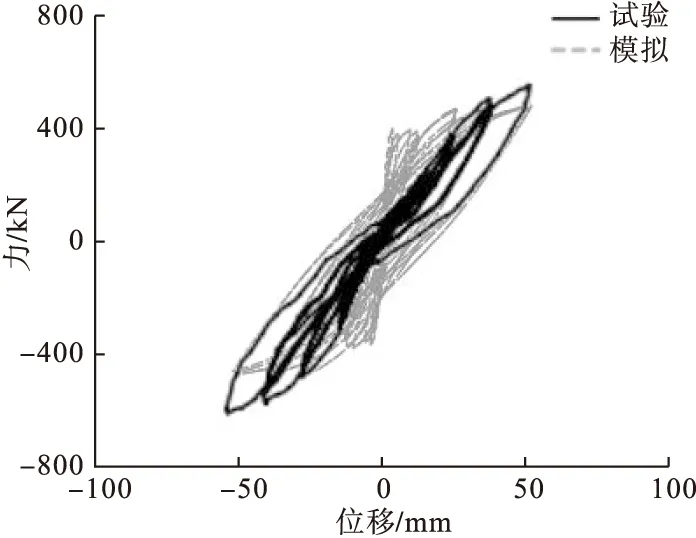
图14 滞回曲线
模拟与试验的骨架曲线如图15所示,对比骨架曲线与文献[1]图8e发现,模拟与试验骨架曲线的走势基本一致,模拟与试验表现出相近的发展规律。
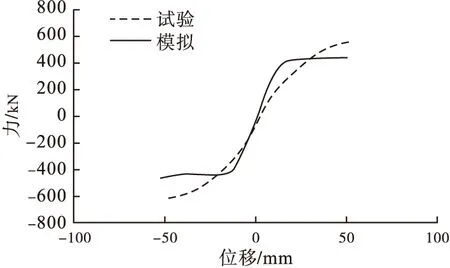
图15 骨架曲线
2.2.2 承载力对比
对比模拟与试验的开裂水平力Fcr、屈服水平力Fy和峰值水平力Fp,见表4所示。

表4 模拟与试验承载力对比
由表4可以看出,开裂水平力与屈服水平力试验结果接近,峰值水平力略低于试验结果;说明“弹簧-杆”模型在装配式浆锚连接结构承载力计算上精度较好,几乎与试验接近。
2.2.3 刚度对比
根据文献[16]的定义,将往复水平力作用下每次循环最大位移的割线刚度定义为等效刚度K,图16为模拟与试验等效刚度退化曲线。由图16可以看出,初始刚度数值几乎一致;随着加载的进行,模拟的刚度逐渐低于试验的刚度;加载结束时二者刚度相差不多,模拟与试验刚度退化趋势大致相同。计算时适当提高“弹簧-杆”模型中弹簧单元刚度,会削弱模拟与试验初始刚度上的差异。
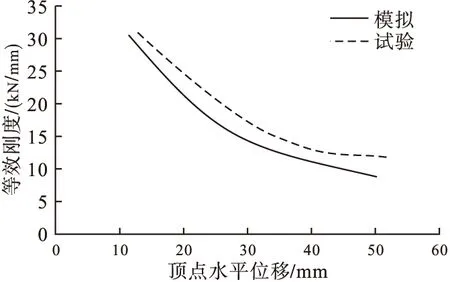
图16 退化刚度曲线
3 结论
应用“弹簧-杆”模型等效浆锚连接的有限元计算得到以下结论。
(1)装配式剪力墙加载的各个阶段,模型的屈服状态与破坏状态基本相同,证明“弹簧-杆”模型高质量完成类似浆锚连接的传力作用;
(2)最大位移与最大应力接近,滞回规律几乎一致,证明“弹簧-杆”模型高质量完成类似浆锚连接的传力作用;
(3)模拟与试验的开裂水平力、屈服水平力和峰值水平力的数值几乎相同,证明“弹簧-杆”模型在装配式浆锚连接结构承载力计算上精度很好;
(4)对比模拟模型与试验试件在加载过程中的等效刚度,本模拟中使用的“弹簧-杆”模型弹簧刚度偏小,在以后的计算中需要适当提高刚度。
