基于K-L散度和TEO的滚动轴承故障频率识别方法

李一平,叶海天,曹 立,赵 琦,徐新胜

(中国计量大学 质量与安全工程学院,浙江 杭州 310018)

滚动轴承是各类旋转机械的关键部件之一,广泛应用于航空航天、交通工具及机械设备等领域。由于复杂的工作环境和高强度的运行,滚动轴承内圈、外圈及滚动体等部件容易损坏失效,影响机械系统的正常运行[1]。滚动轴承发生故障时通常会产生冲击、噪声等表象,由此产生的振动信号是一种有效的故障分析依据,被广泛应用于机械故障诊断中。通常,滚动轴承产生的振动信号中包含了大量的运行状态信息,但振动信号在传递过程中易受到环境噪声和其他部件的干扰,因此,也会造成一些微弱的故障信号被淹没,结果往往收集到的振动信号具有非平稳、非线性、非高斯性和低信噪比的特点[2]。于是,消除振动信号的噪声并有效提取故障特征,对后续滚动轴承的故障诊断及预测性维修工作具有重要的意义。

近年来,专家学者对信号降噪问题,提出了如小波降噪[3]、自适应滤波[3]、经验模态分解[4]、频域特征提取[5]等方法,并在信号特征提取、故障诊断、寿命预测等领域得到了广泛应用。但自适应滤波和小波降噪技术的降噪效果过分依赖滤波器性能的优劣[3],经验模态分解虽然能将信号分解为一系列固有模态函数(IMF),但存在边际效应和模态混叠现象[4];同样,频域特征提取技术也存在计算复杂且降噪效果取决于信号的幅频信息等问题[5]。因此,这些方法在工程实际应用中存在一定的局限性。奇异值分解(Singular Value Decomposition,SVD)作为一种信号消噪方法近年来被广泛的应用于信号处理和统计学等领域[6]。该方法通过重构矩阵及奇异值分解的形式,有效克服了原始信号信息丢失、计算复杂的问题,并通过选取有效的矩阵阶次,可以达到较好的信号降噪效果。对奇异值分解(SVD)方法而言,确定有效的矩阵阶次是保证信号降噪效果的关键。对此,钱征文[6]等根据信号快速傅里叶变换结果中主频率个数来确定有效阶次,采用不同频率成分的几组信号对该方法进行了验证,但不适用强噪声、多频率的信号。周福成[7]等针对频率切片小波变换在强背景噪声条件下,故障特征识别能力不足的缺点,提出根据奇异值差分谱最大值原则,确定有效阶次进行降噪处理,继而利用频率切片小波对降噪信号进行了分析与应用,而奇异值差分谱法在噪声较强时无法保留全部有用信息,因此,实际应用效果也存在不足。沈科宇[8]等通过S-T变换将时域信号向时频域转换,对时频信号矩阵进行奇异值分解,根据奇异值大小对信号降噪并重新构造时域信号,但该方法主观性较强,降噪效果及应用场景也不理想。杨文献[9]等通过分析信号信噪比与奇异熵之间的联系,提出根据奇异熵增量渐进特性来确定信号奇异值分解有效阶次的方法,并采用仿真信号进行了验证,但无法还原真实信号的状态和特点。于是,针对信号数据的实际特点及信号降噪的应用场景和目标,确定奇异值分解的有效阶次,对信号有效降噪尤为重要。

此外,Teager能量算子(Teager Energy Operator,TEO)在20世纪90年代提出,由于它能追踪并计算信号的瞬时能量,因此引起国内外学者的关注并得到广泛应用[10]。王天金[11]等针对滚动轴承故障振动信号中的瞬态冲击特点,提出了基于TEO的频谱分析方法,通过瞬时Teager能量的Fourier频谱识别轴承的故障频率。李辉[12]等利用TEO计算经验模态分解后的齿轮箱轴承振动信号分量,识别齿轮箱轴承的故障部位和类型。向玲[13]等提出了基于变分模态分解和1.5维Teager能量谱的滚动轴承故障特征提取方法。

本文提出一种综合K-L散度和TEO的滚动轴承故障信号降噪及其频率提取方法。首先通过SVD分解原始滚动轴承振动信号得到若干信号分量,为了克服传统奇异值分解中确定有效阶次主观性强且降噪效果不显著的缺点,利用K-L散度计算原始信号与各信号分量的相关性来确定奇异值分解的有效阶次,根据计算所得K-L散度值的差异性去除噪声信号,有效抑制噪声干扰,完成信号降噪和重构。由于滚动轴承发生故障时会产生瞬态冲击,TEO能够及时跟踪信号波形的变化且时间分辨率高,对重构信号进行TEO解调,因而能增强重构信号中微弱的故障频率,提高故障频率识别的准确性。

1 奇异值分解

1.1 奇异值分解原理

假设任意实矩阵Am×n,秩为r,则A的奇异值分解为

A=USVT。

(1)

式(1)中,Um×m、Vn×n为标准化正交矩阵,Sm×n为奇异值对角矩阵,其对角线元素为矩阵A的非零奇异值。

矩阵A的秩为r,从式(1)中除去A的零奇异值,于是,得到A奇异值分解的精简形式:

(2)

式(2)中,σi为矩阵的非零奇异值,ui、vi分别为Um×m、Vn×n的第i个列向量。

1.2 奇异值分解降噪原理

奇异值分解(SVD)降噪是依据信号的信息量与奇异值的对应关系,奇异值越大,包含信息量越多,奇异值越小,包含信息量越少,将包含信息量少的信号分量去除,即去除噪声信号。由式(1)可知,将奇异值按降序排列,可认为有效信号主要由数值较大的奇异值表示。通过设定阈值,将小于阈值的奇异值设为0,即可去除噪声分量,保留原始信号的主要信息,从而完成信号降噪。

SVD降噪的步骤如下。

1) 一维信号转化为矩阵

将一维信号进行SVD分解的前提是将信号序列构造为Hankel矩阵。对于一维振动信号序列X(L)={x1,x2,…,xn},构造Hankel矩阵如下:

(3)

式(3)中,A为m×n阶Hankel矩阵A的行数和列数满足L=m+n-1。

2) 对矩阵进行奇异值分解

A=USVT。

(4)

3) 有效阶次确定

奇异值分解以后,第个非零奇异值构成的信号分量Xi=uieivi。通常,较大的奇异值构成的信号分量包含原始信号更多的信息,通过设定阈值确定保留的奇异值个数,将其余奇异值置为零,即确定奇异值分解的有效阶次。

4) 重构信号

在确定有效阶次后,利用式(2)计算降噪后的信号矩阵X′,对X′的负对角线元素求均值,得到重构信号x(i)=(x1,x2,…,xn),如式(5)所示:

(5)

式(5)中,α=max(1,i-m+1),β=min(n,1)。

重构信号在保留原始振动信号有用信息的同时进行信号的降噪,并将振动信号矩阵还原为一维振动信号,便于进行后续的振动信号解调和故障频率提取。

2 基于K-L散度识别SVD噪声信号

2.1 K-L散度基本理论

K-L(Kullback-Leible)散度是由库尔贝克和莱伯勒提出并命名的,在信息论中得到广泛应用的信号相似性度量方法[14-16]。韩中合[14],王志杰[15],徐统[16]等人先后应用K-L散度进行轴承振动信号的处理,并在故障信号处理上实现了应用。为了更加准确的区分有用信号和噪声信号,本文提出基于K-L散度识别SVD分解噪声信号的方法。

K-L散度是量化两个概率分布之间相似度的指标。设两个概率分布分别为p(x)、q(x),则q相对于p的K-L散度定义为:

(6)

D(p,q)=δ(p,q)+δ(q,p)。

(7)

K-L散度用来衡量两个概率分布的差异性,其物理意义是二者夹角的量度,因此,K-L散度值较大时,表明两个概率分布的差异较大;K-L散度值越小表示两个概率分布的差异越小,即相似度越高。当两个概率分布完全相同时,值为0。

2.2 K-L散度计算

K-L散度需要满足的两个条件:

1) 两个概率分布中各自的概率和必须为1;

2) 若其中一个概率分布为0,则另一个概率分布也必须为0。

设两信号分别为X={x1,x2,…,xn}和Y={y1,y2,…,yn},并且其概率分布为p(x)和q(y)。采用非参数估计法求解信号的概率分布,函数定义为

(8)

式(8)中,p(x)表示信号X的核密度估计函数,k表示核函数,h表示给定的正数(平滑参数或窗宽)。常用核密度函数是高斯核函数,即

(9)

同理,可求得Y的概率分布q(y)。

将信号的概率密度函数分别代入式(6)、(7),即可求得信号X和信号Y的K-L散度值。

2.3 基于K-L散度识别SVD噪声信号

利用K-L散度值来衡量经过SVD分解后各个信号分量与原始信号的“关系远近”。K-L散度值越小,代表此分量与原信号的关系越近,是有用信号;反之,K-L散度值越大,代表此分量与原信号关系越远,是噪声信号。具体步骤如图1。

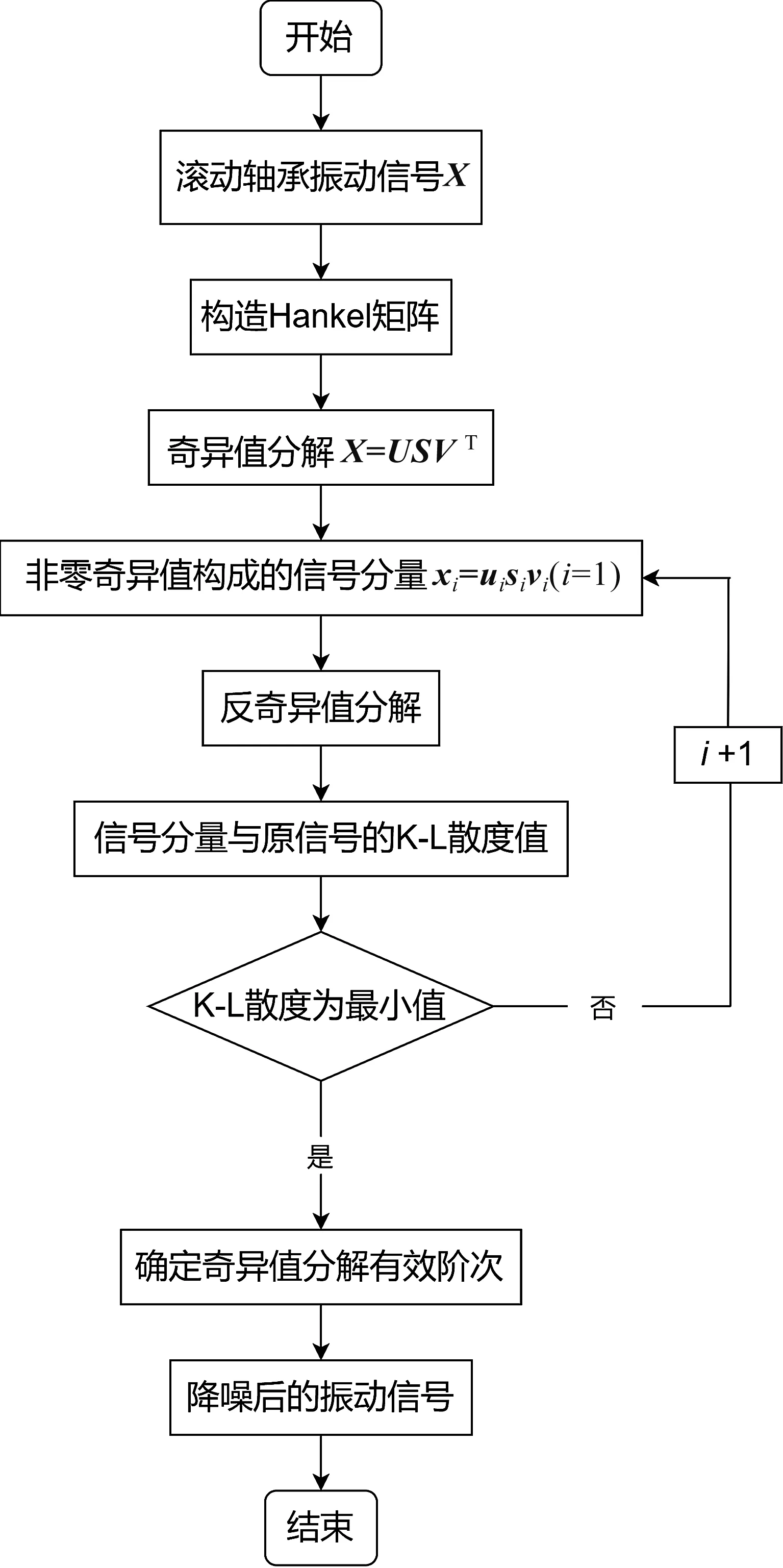
图1 基于K-L散度识别SVD分解噪声信号Figure 1 Recognition of SVD decomposition noise signal based on K-L divergence

3 基于K-L散度和TEO的滚动轴承故障频率提取

TEO是一种非线性差分算子,能够增强信号的瞬时特性,有效提取信号中的瞬态冲击频率。设一组连续时间信号为x(t),TEO定义为φ,则:

(10)

滚动轴承发生故障时会产生瞬态冲击,TEO能够及时跟踪信号波形的变化且时间分辨率高,利用奇异值分解与K-L散度值降噪后的滚动轴承故障信号,经过TEO解调,能有效增强降噪信号的瞬态频率,进而有效提取轴承故障信号中的瞬态冲击频率。

基于K-L散度和TEO的滚动轴承故障频率提取方法步骤如图2。

图2 基于K-L散度和TEO的滚动轴承故障频率提取流程图Figure 2 Flow chart of fault frequency extraction for rolling bearing based on K-L divergence and TEO

4 案例分析

为验证所提方法的有效性,本文采用美国西储大学公开的轴承故障数据集进行试验。该试验驱动电机功率为2.2 kW、电机输出转速为1 730 r/min,采用电火花技术在轴承内圈加工长度为0.178 8 mm,深度为0.279 4 mm的单点故障,轴承信息如表1所示。

表1 轴承信息

依据轴承参数,分别计算型号为SKF62052RS深沟球轴承的转频、内圈故障频率。

轴承旋转频率为

fo=V/60。

(11)

内圈故障频率计算公式为

fi=0.5fo(1+dcosα/D)z。

(12)

其中,V为轴旋转速度,r/min。D为轴承节圆直径,mm。d为滚动体直径,mm。α为接触角,z为滚动体数。

由式(11)、(12)计算可得滚动轴承的旋转频率fo=29.16 Hz,内圈故障频率为f1=158.13 Hz。

本文以内圈振动信号为例,内圈振动信号的幅值图如图4。从图中可以看出由于噪声影响,无法直接识别和提取内圈故障频率。因此,为有效识别和提取被噪声淹没的故障频率,需对内圈振动信号进行降噪预处理。

根据式(3)及Hankel矩阵的构成准则,首先将滚动轴承振动信号构成Hankel矩阵,采用SVD对信号矩阵进行分解,奇异值点的分布如图4所示。

图3 原始信号幅值图Figure 3 Amplitude diagram of original signal

图4 奇异值分布图Figure 4 Singular value distribution

将经过SVD分解后的奇异值代入式(2),逐个计算信号分量与原始信号的K-L散度值,得到K-L散度值最小的信号分量,确定奇异值分解的有效阶次。为了方便观察,取前100个K-L散度值绘图,归一化的K-L散度值如图5所示。可以看出,第8个信号分量的K-L散度值最小,与原信号相似度最高,由式(5)计算得到降噪后的滚动轴承振动信号,如图6。

为验证本文方法的有效性,采用目前被广发使用的有效阶次确定方法——奇异值差分谱法和奇异值中值法作对比,并计算信号降噪指标——信噪比(SNR)和均方根误差(RMSE)。

奇异值差分谱法是将奇异值差分谱的最大突变作为有效阶次,为了方便观察,取前100个奇异差分值绘图,如图7所示。选取差分值最大值对应的奇异值186.5作为阈值,选取有效阶次为2,得到降噪后的滚动轴承振动信号,如图8。

图5 归一化K-L散度值Figure 5 Normalized K-L divergence

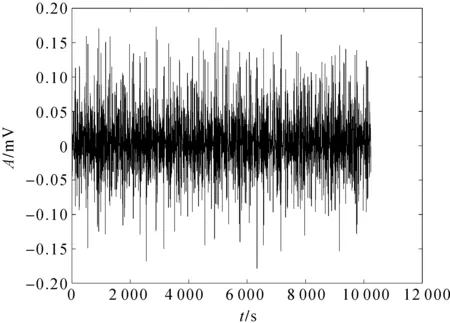
图6 基于K-L-SVD方法降噪幅值图Figure 6 Noise reduction amplitude image based on K-L-SVD method

图7 奇异值差分谱Figure 7 Singular difference spectrum

图8 奇异值差分谱法降噪幅值图Figure 8 Singular value difference spectrum method for noise reduction amplitude diagram

奇异值中值法是将奇异值按从大到小的顺序进行排列,取奇异值的中值作为有效阶次。假设奇异值个数为n,若n为偶数,则中值的为第n/2个奇异值和第(n+2)/2个奇异值之和的平均数,若为奇数,则中值为第(n+1)/2个奇异值。由奇异值中值法降噪得到的信号如图9。

图9 奇异值中值法降噪幅值图Figure 9 Singular value median method for noise reduction amplitude chart

信噪比(SNR)表示信号与噪声的比值,信噪比的值越大则代表噪声越小。均方根误差(RMSE)表示计算真实值与预测值的比值,均方根误差越小则代表降噪效果越好。计算上述三种方法所得降噪信号的SNR和RMSE如表2所示。从表中可以看出本文所提方法在增大SNR值的同时降低RMSE值,降噪效果更优。

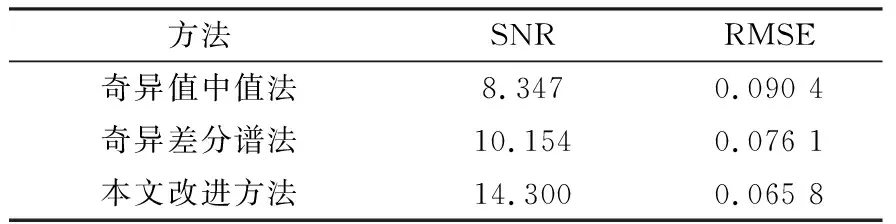
表2 三种方法的降噪指标

由于滚动轴承发生故障时会产生瞬态冲击,且早期微弱的故障信号易被噪声淹没。利用TEO对降噪后的信号进行解调,增强信号中微弱的故障信号,以便对滚动轴承的故障频率进行准确识别。经过TEO解调后的滚动轴承振动信号的时频图如图10。

图10 TEO解调信号时频图Figure 10 Time-frequency diagram of TEO demodulation signal

从图10中可以看出,经过TEO解调后滚动轴承的转频、内圈故障特征频率、内圈故障特征频率倍频、内圈故障特征频率与转频之和的频率得到增强,说明该方法在滚动轴承故障特征提取方面有很好的效果。

为了进一步验证TEO解调对滚动轴承故障频率识别的有效性,选用快速傅里叶变换(Fast Fourier Transform,FFT)和包络谱解调分别对振动信号进行分析,得到结果如图11和图12所示。

从图中可以看出,振动信号经快速傅里叶变换后存在频谱泄露的问题,使早期微弱故障信无法识别;包络谱解调后虽然可以突出故障频率,但存在频谱混叠的问题,增加了故障频率识别的复杂性。综上所述,本文利用TEO对振动信号进行解调可以增强早期微弱故障信号并准确识别故障频率。

图11 快速傅里叶变换信号时频图Figure 11 Time-frequency diagram of FFT

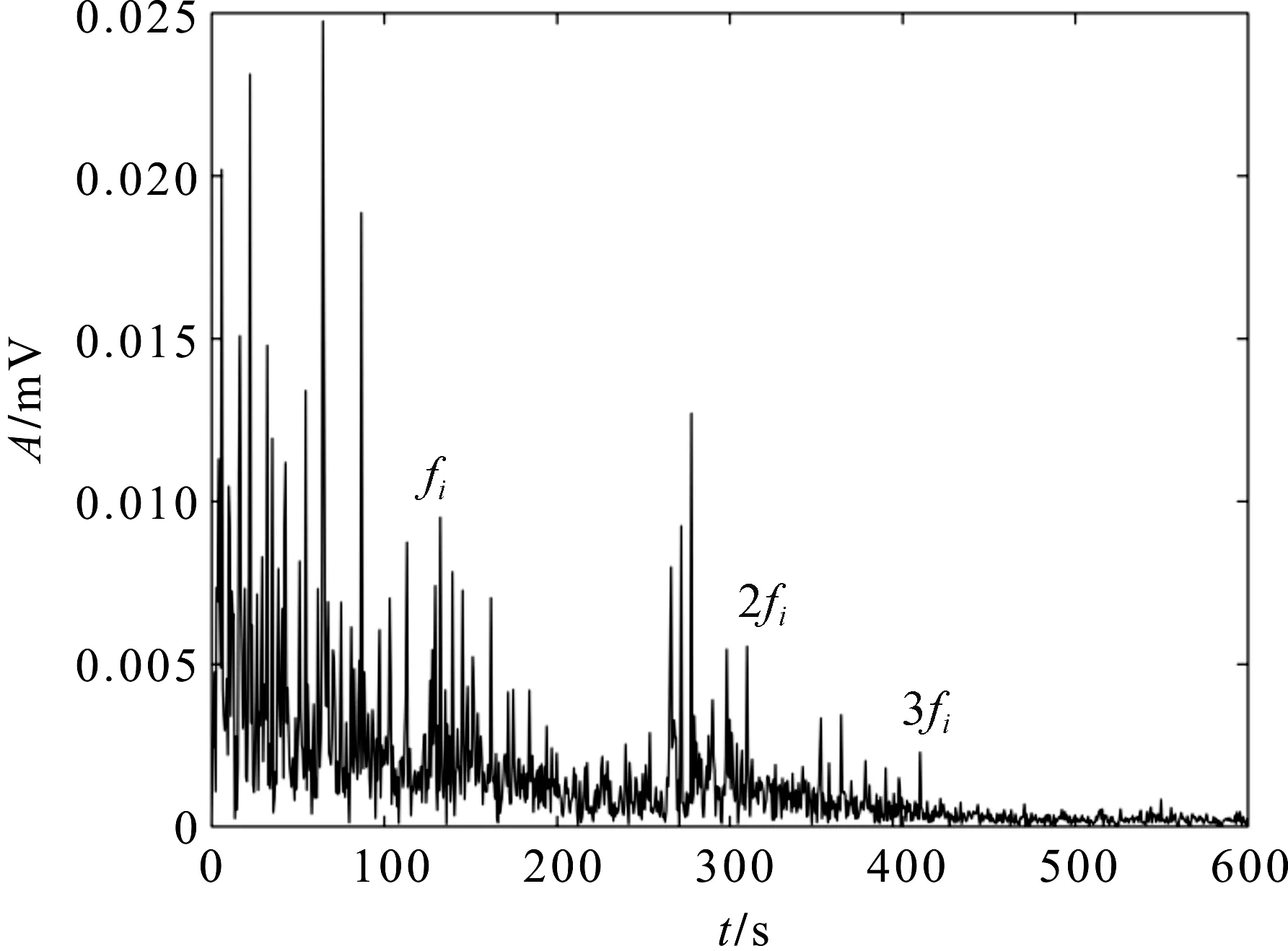
图12 包络谱解调信号时频图Figure 12 Time-frequency diagram of envelope spectrum demodulation signal

5 结 论

滚动轴承振动信号具有非平稳、非线性、非高斯性和低信噪比的特点,同时,传统的奇异值分解中阈值选取方法不能有效分离有效信号和噪声信号;然而利用K-L散度和TEO相结合的方法,能够有效提取滚动轴承故障频率。

本文利用SVD与K-L散度对滚动轴承振动信号进行降噪,克服了传统奇异值分解确定有效阶次方法中不确定性、主观性强的缺点,根据不同信号分量与原始信号K-L散度值的差异性,将噪声信号从中分离出来,从而有效抑制噪声的干扰,提高信号的信噪比。同时,通过TEO对降噪信号解调分析,能够增强信号中微弱的故障频率,与其它信号解调方法相比,提取到的故障频率更加全面、清晰。

本文采用美国西储大学滚动轴承数据集进行了验证,为滚动轴承的故障振动信号分析提供了一种可行的办法。