Lévy噪声驱动下具有非单调发生率的随机SIQR传染病模型

郭英佳, 徐小芮, 李晓岚

(北华大学 数学与统计学院, 吉林 吉林 132013)

0 引 言

传染病严重危害人类的健康, 目前控制传染病传播的主要方法之一是对感染者采取有效隔离, 这种方法在控制麻疹、乙肝、天花等人类传染病中发挥了重要作用[1-2]. 在新冠肺炎爆发期间, 我国通过采取相应的隔离措施, 有效降低了该疾病的传播, 使疫情得到有效控制.

在传染病动力学中, 对带有隔离的传染病模型研究目前已取得了丰富成果[3-9]. 该方法将人群分为易感者(S)、感染者(I)、隔离者(Q)、恢复者(R)四类, 所建立的确定型传染病模型通常称为SIQR传染病模型. 研究表明, 疾病的传染率对研究传染病具有重要作用[10-11], 而非线性传染率能更好地反应疾病传播的特点. 文献[12]给出了一种一般的非线性传染率g(I)S=kIpS/(1+αIq), 其中1/(1+αIq)表示易感者心理影响对疾病的抑制作用,kI表示疾病的传播力度. 考虑到某些严重传染病, 当传染数目增大时, 易感者的心理影响会对疾病产生相应的抑制作用, 文献[13]利用形如g(I)=kI/(1+αI2)的非单调传染率有效刻画了这种现象, 建立了如下具有这类非单调传染率的确定型SIQR传染病模型：

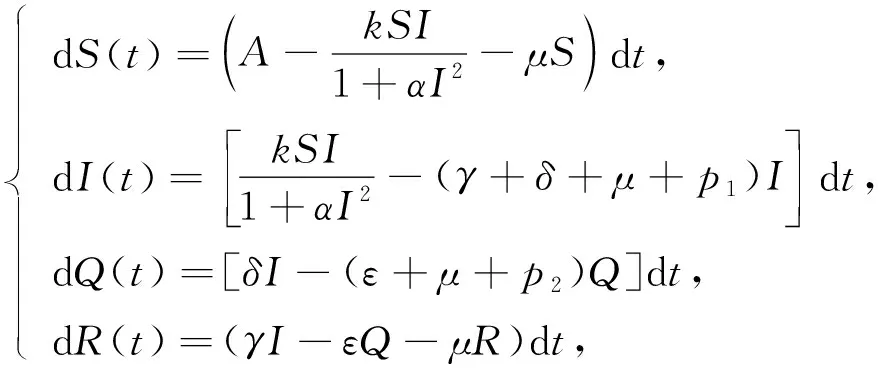
(1)

并研究了系统(1)在平衡点的稳定性, 得到如下结果：

定理1[13]当阈值R0<1时, 系统(1)只存在无病平衡点E0且是全局渐近稳定的, 此时疾病将最终灭绝; 当阈值R0>1时, 系统(1)的无病平衡点E0不稳定, 地方病平衡点E*是全局渐近稳定的, 此时疾病将持续存在.

考虑到实际应用中环境噪声处处存在, 且会对传染病系统产生一定影响, 因此, 在传染病动力学模型中加入随机噪声更具有实际意义. 结合疾病的实际传播情况, 文献[14]在文献[13]的基础上, 建立并研究了如下由白噪声驱动的随机SIQR传染病模型：

(2)

得出结论： 当基本再生数不大于1时, 在一定条件下随机模型(2)在无病平衡点附近具有渐近稳定性； 当基本再生数大于1时, 该随机系统的解在地方病平衡点附近振荡.

考虑到自然界中还存在一些突变现象, 而布朗运动无法很好地描述这些非常态现象, 这些不连续噪声通常可用跳过程或一般的Lévy噪声描述. 因此, 本文建立并研究一类由Lévy噪声驱动的具有非单调发生率的随机SIQR传染病模型：

(3)

由于系统(3)的前3个方程不含有R, 所以下面只需考虑系统(3)前3个方程构成的子系统:

(4)

1 全局正解的存在唯一性

为研究系统(4)的动力学行为, 首先要考虑系统(4)是否存在唯一的全局正解. 为此, 需对跳扩散系数做如下假设： 假设对于每个m>0, 均存在Lm>0, 使得:

(5)

|ln(1+Di(u))|<∞,Di(u)>-1,i=1,2,3,u∈Y,

(6)

其中F1(x,u)=D1(u)S(t),F2(x,u)=D2(u)I(t),F3(x,u)=D3(u)Q(t), |x|∨|y|≤m.

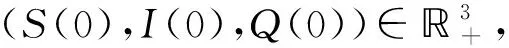
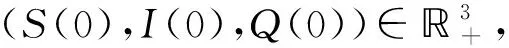
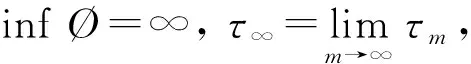
其中a是正常数. 显然当u>0时,u-1-lnu≥0, 因此V函数具有非负性. 根据It公式, 有

其中,

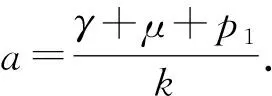
有

(8)

结合式(8), 将式(7)两端从0到τm∧T积分并取期望, 有

E[V(S(τm∧T),I(τm∧T),Q(τm∧T))]≤V(S(0),I(0),Q(0))+KT.

令Ωm={ω|τm≤T,m≥m1}, 则有P(Ωm)≥ε.对于每个ω∈Ωm,S(τm,ω),I(τm,ω),Q(τm,ω)中至少有一个等于m或1/m.若S(τm,ω)=m或1/m, 则有

若I(τm,ω),Q(τm,ω)中存在一个等于m或1/m, 则

于是

从而

这里IΩm表示Ωm的示性函数. 令m→∞, 有∞>V(S(0),I(0),Q(0))+KT=∞, 矛盾, 因此假设不成立, 证得τ∞=∞ a.s. 从而有τe=∞ a.s., 表明系统的解在有限时间内不会爆破, 是全局存在且唯一的. 证毕.

2 无病平衡点附近解的渐近行为

定理3假设条件(5),(6)成立, 且满足：

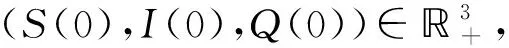
这里

其中,

结合式(10), 将式(9)两端从0到t积分并取期望, 有

将式(11)两端同时除以t, 得

从而有

证毕.

注1定理3表明, 系统(4)的解将在无病平衡点E0附近振动, 其振动强度与σi和Di(i=1,2)有关, 且随机扰动越小, 解的振动越弱, 此时系统的解将越接近确定型SQIR模型的无病平衡点E0, 疾病将会消失.

3 地方病平衡点附近解的渐近行为

当R0>1时, 确定型SIQR模型存在地方病平衡点E*(S*,I*,Q*), 且是全局渐近稳定的. 下面讨论随机系统(4)的解在地方病平衡点E*附近的渐近行为.

其中

证明: 首先分别定义函数

令V=V1+V2+V3, 有

因此, 有

对式(13)两端从0到t积分再取期望, 有

将式(14)两端同时除以t, 并令t→∞, 有

从而有

注2定理4表明, 在某些假设条件下, 系统(4)的解将做随机振动, 且振动强度与随机噪声强度σi和Di(i=1,2,3)有关. 随机噪声强度越小, 模型的解越接近地方病平衡点, 此时疾病将会持续存在.