分数阶微分方程无穷多点边值问题正解的存在性
2021-11-26尚淑彦
尚 淑 彦
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
分数阶微分方程在电磁学、力学、医学、扩散、控制、信息处理等领域应用广泛. 目前, 分数阶微分方程的研究主要集中在非线性分数阶微分方程边值问题正解的存在性、多重性和唯一性[1-11].
文献[1]利用Krein-Rutman定理研究了m-点边值问题:

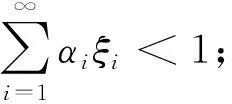

受上述研究工作启发, 本文考虑问题
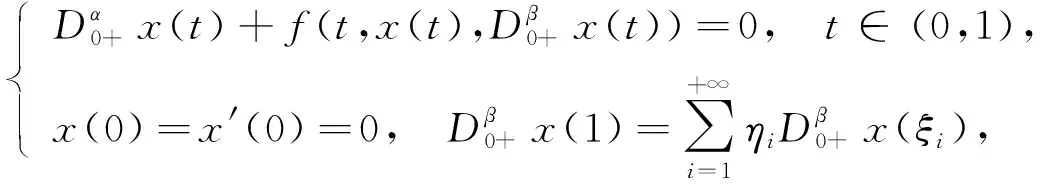
(1)

1 预备知识
定义1[12]函数f: [0,∞)→的α>0阶Riemann-Liouville分数积分定义为
定义2[12]函数f: [0,∞)→的α>0阶Riemann-Liouville分数导数定义为
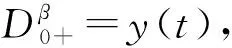

(2)
由文献[5]知, 增函数
有唯一的根τ*>0.
显然, 共振问题(2)等价于非共振问题:

(3)
其中τ∈(0,τ*],τ<1. 记

(4)
引理1设g∈C[0,1], 则分数阶边值问题

(5)
有唯一解
证明:y(t)的证明过程与文献[3]类似, 故略. 下面证明
收敛. 由式(4)得

(6)

由于
故G(1)在[0,1]上收敛.G(1)各项绝对值组成的级数为
用比式判别法可得
因此|G(1)|收敛, 从而G(1)绝对收敛. 记

用比式判别法可得


收敛.
记K(s)=(1-s)α-β-2-s在[0,1]上严格递减, 且K(0)=1,K(1)=-1, 则K(s)在(0,1)上有唯一的根s*, 满足
s*=(1-s*)α-β-2.
引理2H(t,s)有下列性质:
ρ1s(1-s)α-β-1tα-β-1≤H(t,s)≤ρ2s(1-s)α-β-1,t,s∈[0,1],
其中
引理2的证明过程与文献[3]类似, 故略.


1) ‖Ax‖≤‖x‖, ∀x∈P∩∂Ω1; ‖Ax‖≥‖x‖, ∀x∈P∩∂Ω2;
2) ‖Ax‖≤‖x‖, ∀x∈P∩∂Ω2; ‖Ax‖≥‖x‖, ∀x∈P∩∂Ω1.

设P是Banach空间E中的一个锥,Pr={x∈P|‖x‖ 考虑P上一个非负连续凹泛函α(x), 即α:P→[0,∞)连续, 且对∀x,y∈P, 0≤t≤1, 有 α(tx+(1-t)y)≥tα(x)+(1-t)α(y). 下面恒用P(α,a,b)表示集合{x∈P|a≤α(x), ‖x‖≤b}, 这里0 1) {x|x∈P(α,b,d),α(x)>b}≠Ø, 且当x∈P(α,b,d)时, 恒有α(Ax)>b; 3) 当x∈P(α,b,c)且‖Ax‖>d时, 恒有α(Ax)>b. 注1如果d=c, 则由引理4中条件1)可推出条件3). 设 引理5[3]设算子A:Q→E定义为 则A:Q→Q是全连续的. 为方便, 记 定理1令g(t,x,y,τ)=f(t,x,y)+τy, 设存在两个正数r2>r1>0, 使得下列条件成立: 则问题(1)至少存在一个正解, 且r1<‖y‖ 证明: 记Ω1={y∈Q|‖y‖≤r1}, 对y∈∂Ω1, 有0 因此 ‖Ay‖≥‖y‖, ∀y∈Q∩∂Ω1. 记Ω2={y∈Q|‖y‖≤r2}, 对y∈∂Ω2, 有0 因此 ‖Ay‖≤‖y‖, ∀y∈Q∩∂Ω2. 由引理3可知, 问题(1)至少存在一个正解, 且r1≤‖y‖≤r2. 证毕. 对∀R≥r>0, 定义 定理2假设存在0 则问题(1)至少存在3个正解y1,y2,y3. 首先, 设{xn⊂Q},x∈Q且xn→x(n→∞), 即 因为 且 所以 从而 故α是连续泛函. 其次, ∀x,y∈Q,α:Q→[0,∞)连续, 0≤λ≤1, 有 显然α(x)是在Q上的非负连续凹泛函, 且α(x)≤‖x‖. 对t∈[δ,1-δ], 有 则引理4中条件1)成立. 3) 证明引理4中条件3)成立. 对∀y∈Q(α,b,c), 有‖Ay‖≥d,dx*>b.因此 综上, 本文分别用锥拉伸与压缩不动点定理和Leggett-Williams不动点定理, 得到了问题(1)至少存在1个正解和3个正解的结果. 特别地, 在Leggett-Williams不动点定理中, 对问题(1)中的非线性项f的限制更多则条件更强, 得到的结果相比于锥拉伸与压缩不动点定理的结果更好.

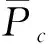
2 主要结果









