超临界CO2脱附作用调控负载纳米颗粒结晶动力学研究

乔国岳，刘居陶，孙剑飞，徐琴琴，银建中

（1 大连理工大学化工学院，辽宁大连116024； 2 青岛科技大学机电工程学院，山东青岛266061）

引 言

结晶在材料制备领域有着广泛的应用，而成核是结晶过程的关键环节，决定着晶体的结构和性能。成核是一个相变过程，经典成核理论（classical nucleation theory, CNT）认为成核是驱动力与阻力（过饱和度与表面自由能增加）之间的一个竞争过程[1]。CNT 假设成核是一步过程，其中团簇自发聚集产生一个临界晶核。根据这个假设，小于临界晶核的晶体会逐渐分解，而大于临界晶核的晶体会不断增大。

自20 世纪90 年代，超临界流体技术用于纳米材料制备逐渐受到重视。发展了诸如超临界溶液快速膨胀法、超临界流体反溶剂法、超临界流体微乳液法以及超临界流体沉积法等技术[2-4]。其中，超临界溶液快速膨胀（rapid expansion of supercritical solutions, RESS）技术在制备超细微粒方面表现突出，相应的结晶理论工作也一度成为研究热点。1990 年，Debenedetti[5]研究了菲-CO2体系沿三种不同膨胀路径（等压预热后等温膨胀、等压预热等熵膨胀、等压预热后等焓膨胀）下，均相成核速率、过饱和度和成核数量的变化，发现成核速率是溶剂膨胀、减压冷却和高过饱和度几个因素共同作用的结果。尽管过饱和度很大（＞106），受冷却和膨胀制约，最后形成相对平坦的成核速率曲线。当表面张力为0.02 N/m 时，计算出的反应器中成核速率极限为104cm-3·s-1。为了考察颗粒大小和粒径分布沿喷嘴的变化趋势，Debenedetti等[6]研究了二元超临界溶液体系（菲-CO2）的结晶过程。溶解菲的超临界CO2溶液经喷嘴膨胀时，溶质过饱和而析出。假设流动是稳定一维无黏性流，绝热膨胀。据此建立了菲-CO2体系在亚音速收敛喷嘴膨胀过程中完整的晶体成核和生长数学模型。研究结果表明，在喷嘴中可达到的成核速率为1027cm-3·s-1左右，提高预膨胀温度可以增大颗粒尺寸。而后，Türk等[7-10]基于纯溶剂一维稳态流动模型，考察了胆固醇-CO2、苯甲酸-CO2和苯甲酸-三氟甲烷三个体系，研究溶解度、表面张力对成核能及膨胀过程中成核速率的影响。将经典成核理论扩展到非理想流体的方程计算成核速率，并与实验结果比较，发现其模型可用于定性分析。2005 年，Hirunsit 等[11]提出一维流动模型，用以描述超临界溶液快速膨胀的成核过程。模型假设RESS 膨胀路径由毛细管内和超音速自由射流两部分组成，考虑喷嘴内壁面摩擦和超音速自由射流区与周围环境的热交换。对布洛芬/超临界CO2体系过饱和度、成核速率、临界晶核尺寸和临界晶核数浓度进行计算，结果表明：当流体离开喷嘴出口进入超音速自由射流区域时，过饱和度会达到约109；临界晶核尺寸减小，晶核浓度增大；预膨胀压力、预膨胀温度以及喷嘴长度对流场性质影响不大。2007 年，Weber 等[12]推导了一套估算RESS 产生的颗粒平均直径的解析方程，用该模型得到的结果与实验结果吻合较好。由于冷凝生长只有几微秒，经小长径比圆柱形喷嘴所产生的颗粒在到达临界截面前其平均直径介于20～50 nm。此外，还比较了三种不同凝固生长驱动机制，发现滑移流差异的影响最有可能显著改善RESS 模型。2015 年，Yamamoto等[13]以超临界CO2为溶剂、萘为溶质研究其RESS 工艺中的结晶过程，发现喷嘴内压力对喷嘴入口压力很敏感。喷嘴入口压力变化决定喷嘴内流体达到临界压力的位置，进而影响萘颗粒成核的起始位置。

经过几十年发展，人们对成核理论的研究与认识不断深入，发展了不同工况下的数学模型。应用超临界流体制备纳米颗粒具有独特优势，过程绿色且泄压过程中可实现溶剂与溶质的快速分离，颗粒形貌和尺寸可控性强。超临界流体沉积法（supercritical fluid deposition，SCFD）是一种可在纳米孔内高效沉积纳米颗粒以制备负载型纳米材料的技术。在作者前期研究过程中发现，此方法无论是采用有机金属前驱物还是以共溶剂辅助溶解无机盐为前驱物，均可在纳米孔道内获得高分散的纳米颗粒（nanoparticles,NPs），然而其载体内所负载的NPs的平均粒径的可调性较差[14-22]，尤其是获得1 nm晶核尺寸的NPs 存在一定的难度。究其原因，在超临界沉积过程中载体对于前驱物的亲和力大于超临界CO2，致使前驱物不断在载体表面分散，然而这一分散过程存在一定的随机性。而这种随机性，在以共溶剂辅助超临界CO2溶解无机盐的沉积实验中，则表现为共溶剂分子在载体表面浓集的随机性。以介孔SiO2材料SBA-15 载体为例，其本身并不能直接吸附无机盐离子，而需要共溶剂率先在其表面浓集，通过无机盐溶解其中而被间接吸附于SiO2材料之上，同时超临界CO2聚集在共溶剂分子周围。

本文通过对经典成核理论和超临界流体中的成核理论模型分析，评价SCFD 过程超临界条件下影响晶体成核速率和控制颗粒粒径尺寸的关键因素。在泄压阶段，如果逐渐提高泄压速率，SBA-15孔道内围绕在共溶剂周围的scCO2则会快速解吸，致使部分共溶剂从载体表面脱附，在载体表面无机盐前驱物存在析出的可能性。而通过群体平衡模型（population balance model，PBM）对于超临界反溶剂（supercritical anti-solvent，SAS）成核路径的分析，在超临界条件下脱附的CO2成为诱导前驱物成核的新因素，且其成核速率可以由CO2的解吸流量来控制，为研究在纳米孔道内SAS 工艺的实现提供了一个条件。纳米孔道内前驱物晶体的形成，使得纳米复合材料的分散相在焙烧过程中不易团聚，有效控制载体所负载的NPs的平均粒径及尺寸分布。

1 成核理论分析与评价

1.1 经典成核理论

经典成核理论认为，结晶成核过程中，随着新表面形成，体相自由能不断减小，而表面自由能不断增大[23]。对于球形核，其成核过程中自由能变化如式(1)所示:

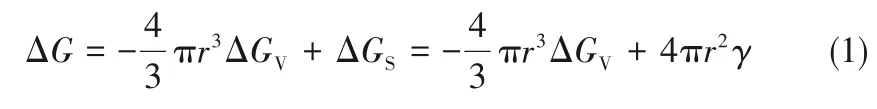
式中，ΔG为单位体积相变自由能变化量；ΔGS为新表面形成时表面自由能差；ΔGV为新相产生时单位体积体相自由能变化量；r为晶核半径；γ为新相表面能。

根据经典成核理论和Arrhenius 方程，稳态成核速率可表示为：

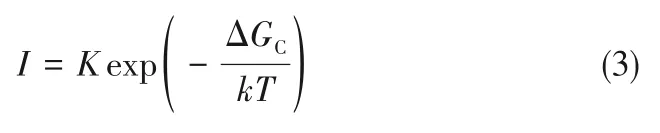
式中，K为指前因子，它与单位体积内潜在成核位点数、原子、分子或离子迁移速度以及黏附率等有关。Becker 等[24]提出准稳态成核过程速率方程式如下：

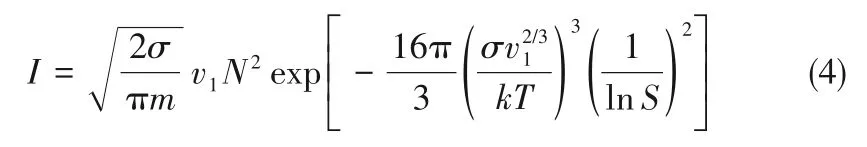
式中，I为成核速率；σ为表面张力；m为溶质分子量；v1为溶质分子体积；N为可凝聚分子数量；k为玻尔兹曼常数；T为温度；S为过饱和度。

1.2 超临界溶液快速膨胀法成核理论模型

1.2.1 Debenedetti模型 Debenedetti课题组[25]在 经典成核理论的基础上，考虑到超临界流体的非理想性，将理想流体的成核动力lnS修正为lnS-Kye1(S-1)，其中K值在临界点附近有非常大的峰值，ye1为在超临界流体中溶质达到溶解平衡时的摩尔分数，其修正后的临界晶核半径r*如式（5）所示，对超临界溶液在喷嘴内快速膨胀形成气溶胶的成核过程，建立数学模型[25]，微孔喷嘴中溶质成核速率I如式（6）所示。

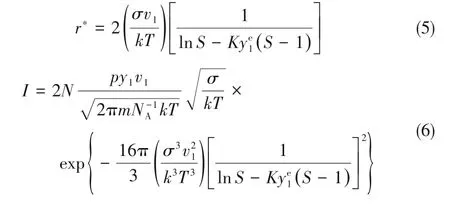
式中，N是单位体积内的溶质分子个数；P是反应压力，Pa；y1是溶质摩尔分数；NA为阿伏伽德罗常量，6.022×1023mol-1。

1.2.2 Türk 模型 Türk[7]基于纯溶剂一维稳态流动,考虑超临界流体非理想性，对经典成核理论进行修正，提出了如下的超临界溶液快速膨胀成核模型(喷嘴内)：

式中，θ为非等温因子，稀溶液等于1；αC为冷凝系数，一般取0.1；M为可凝结分子数；ρM为溶液密度；yE为溶质摩尔分数。

1.3 模型的分析比较

对比成核速率I的计算式[式（4）、式（6）、式（8）]可以看出：CNT 模型和Türk 模型的指数项一致，Debenedetti 模型则在指数项中用(S- 1)修正成核驱动力lnS，考虑超临界流体非理想性对于成核速率的影响；与CNT 模型相比较，Debenedetti 模型和Türk 模型在指前因子项中分别引入了反应压力和相变对于成核速率的影响。对比临界晶核半径r*的计算式[式（5）、式（7）]可以看出，Debenedetti 模型比Türk 模型多了(S- 1)这一项，且在临界点附近K出现峰值，而逐渐远离临界点K则显著降低，考虑到超临界流体非理想性对于临界临界晶核半径r*的影响。另外，对于过饱和度，Debenedetti模型适合于无限稀释溶液才严格有效（比如溶质浓度为10-5mol/cm3），而Türk模型对Debenedetti 模型进行完善，对溶液浓度不加严格限制。可见对于成核速率I而言，Debenedetti 模型和Türk 模型均是在CNT 基础之上分别引入修正系数，说明超临界流体中成核路径的特殊性。而为了研究表面张力σ、温度T以及过饱和度S三个主要参数影响成核速率I的一般规律，选择CNT 模型作三维响应面图形，分别考察三者对成核速率的影响，如图1所示。

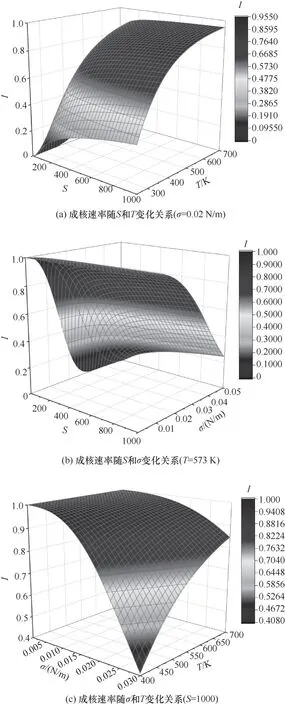
图1 基于CNT的成核速率变化规律的三维响应面图形Fig.1 A three-dimensional response surface of the nucleation rate variation of CNT

如图1（a）所示，当晶体材料表面张力σ为0.02 N/m，成核速率I随过饱和度S和温度T的提高而增大，且过饱和度和温度的交互作用逐渐减弱。温度高于400 K，过饱和度大于150时，成核速率I呈现急剧增加趋势。如图1（b）所示，当反应温度T为573 K，成核速率I随过饱和度和表面张力增大而减小，且过饱和度和表面张力的交互作用逐渐增强。可见与图1（a）的反应温度相比较，晶体材料表面张力σ对于成核速率的影响更为显著，且即使在很高的过饱和度S下，成核速率也会明显降低。将温度T和表面张力σ作为变量分析，如图1（c）所示，当流体的过饱和度S为1000，成核速率I随温度T和表面张力σ提高而减小，且温度和表面张力的交互作用始终显著。可见温度T和表面张力σ虽然都能显著影响成核速率，然而表面张力σ的增加则能显著降低成核速率。从溶质成核路径出发，其材料本身的表面张力σ是一定的，也就是说一定温度条件下溶液的过饱和度将对应一定的成核速率。换言之，材料本身的表面张力越低，则在同样的条件下成核速率越高，对于一定质量的溶质，有利于制备工艺获得粒径分布越窄的晶体颗粒。

2 超临界下CO2脱附过程中纳米孔内的结晶过程

在结晶工艺中更高的成核速率，则同时面对晶核的团聚与长大；粒径分布的调控难度大，对于高表面能的纳米晶体，则调控难度进一步增加。通常在控制溶质浓度的同时，通过调控结晶成核的时间，来调控纳米晶体的形貌与尺寸，并将其分散于多孔载体中，来抑制其在应用的过程中出现的团聚[26-28]。前面介绍了超临界溶液在喷嘴内快速膨胀形成气溶胶的数学模型。依据奥斯瓦尔德熟化（Ostwald ripening）对晶核生长的描述，第二相颗粒析出成核后，由于小尺寸颗粒Gibbs 自由能高于大颗粒，导致小尺寸颗粒周围的母相组元浓度高于大颗粒周围的母相组元浓度，两处的母相组元浓度梯度导致了组元向低浓度区扩散，为大颗粒继续吸收过饱和组元而继续长大提供物质供应，最终致使小颗粒溶解消失[29]。分析RESS的成核路径可知，之所以能够获得小尺寸的NPs（2～15 nm），其原因在于一定温度、压力下的超临界流体在快速膨胀过程中实现了溶剂与溶质的瞬间分离（10-8～10-5s），其晶核生长路径受到控制。同时，这一瞬时的分离也导致体系中出现了极高的过饱和度，进而实现了在喷嘴内瞬间产生大量晶核。

对于粒径尺寸接近晶核尺寸的约2 nm NPs 而言，其晶核形成初期的时间是极短的。2013 年Chakraborty 等[30]利用分子动力学模拟分析NaCl 水溶液结晶的早期阶段，其有序晶核约在150 ns形成，晶核尺寸约为1.6 nm。2017 年Dashtian 等[31]模拟了介孔材料内NaCl水溶液结晶成核的过程，由于纳米孔道壁面对于晶核形成的影响，约在30 ns有序晶核形成。可见，RESS工艺的膨胀时间与晶核的形成时间相接近。换言之，之所以该工艺能够获得约2 nm NPs，是由于所产生的晶核还未来得及在母相中继续生长，即与母相分离。而SCFs以音速推进机械扰动，抑制了晶核的团聚，使得成核粒径分布变窄。

在以共溶剂辅助超临界CO2溶解无机盐前驱物的沉积过程中，由于所采用的共溶剂往往含有—OH，能够和二氧化硅载体表面的—OH 形成氢键，而CO2与载体的相互作用要弱于共溶剂分子与载体的相互作用[32-35]。因此，超临界CO2携带溶解的共溶剂分子和无机盐前驱物进入载体的孔道，共溶剂分子占据吸附位置，并不断浓集；无机盐溶解于共溶剂中而被间接吸附于载体表面，直至吸附平衡。SBA-15 硅基材料具有二维六边形通孔结构，且孔道壁面存在微孔[19,36]。作者[35]在之前的研究中发现，利用乙二醇（1.0 ml）和水（0.5 ml）作为共溶剂，在20 MPa、50℃下超临界CO2沉积法中，可将前驱物硝酸铜（200 mg）高效沉积于SBA-15（200 mg）孔道中。随着沉积时间的延长，在缓慢泄压（0.008 MPa/min）至常压后，样品经干燥并在500℃空气中焙烧，其孔道内获得了高分散的平均粒径为（4.9 ±2.0）nm 的CuO NPs 分布，其样品Cu 的担载量达到17.8%（质量）。然而，在沉积实验中即使降低前驱物浓度所制备复合材料的Cu 担载量减小至4%（质量），也并未能使NPs 平均粒径降至4 nm 以下。换言之，虽然本沉积法可以利用超临界CO2的传质能力，使得共溶剂在SBA-15 孔道内获得了高效分散，但是对于接近晶核尺寸（约1 nm）的NPs 而言，在焙烧阶段介孔载体的孔道内，有足够的空间发生晶核团聚；并且这种团聚具有随机性，导致所获得的CuO NPs 的尺寸很难降至4 nm 以下。而与大于4 nm 的NPs相比较，直径小于4 nm 的NPs具较高化学活性，常常作为催化化学反应的活性中心[37-38]。

为了实现在沉积实验中有效调控NPs 粒径尺寸，在接下来的研究中采用相同的沉积条件，沉积反应结束后由原来的缓慢泄压，提升超临界CO2的泄压速率，引入CO2脱附作为影响NPs 尺寸分布的新因素。利用透射电子显微镜（transmission electron microscopy，TEM）观察所制备的CuO/SBA-15 样品，在恒温50℃下20～14 MPa 的初始压降区间，伴随泄压速率的不断增加（0.05、1.2 及18 MPa/min），SBA-15载体孔道内的CuO NPs的平均粒径逐渐变小，其标准差变小[（6.5 ± 2.9）、（2.2 ± 1.0）及（1.8 ± 0.6）nm]。然而与缓慢泄压的样品金属担载量相比较，伴随泄压速率（0.05 MPa/min）的升高Cu担载量降为7.2%，而其平均粒径却增长为（6.5 ±2.9）nm[39]，说明该方法调控NPs 尺寸的机理与金属担载量之间并不存在直接的对应关系。

究其原因，一方面虽然快速解吸的CO2机械扰动作用能够带走载体表面吸附的共溶剂和部分硝酸铜前驱物，但是scCO2的快速泄压过程在实现调控孔道内NPs 尺寸的同时，也实现了载体表面的清洗，致使复合材料的Cu 担载量大幅度降低；另一方面，伴随泄压速率进一步升高样品的Cu担载量又出现上升趋势（7.2%、8.5%及12.3%），且示孔道内颗粒的数量也随着泄压速率的提高而增多。作者在之前的研究中还提出了CO2脱附的过程中能够引起无机盐前驱物在孔道表面发生非均相成核，即随着泄压速率的提高成核速率增大[39]。值得注意的是，所用SBA-15 的平均孔径为4.9 nm，CO2脱附过程中的机械扰动在纳米孔道内受孔道壁面的限制，可能并不利于NPs 的粒径均一化。因此，虽然在前面的研究中，对已经获得的实验结果给出了相应的解释，然而对于该方案能够在纳米孔道的限域空间内，有效调控NPs粒径及其分布的机理，仍然存在认识盲区。即伴随泄压阶段泄压速率的提升，超临界下CO2脱附作用的增强，与载体孔道内NPs 粒径分布的变化规律，二者之间是否存在对应的数学模型。

在20 MPa、50℃下沉积实验结束后，超临界CO2聚集于吸附在SBA-15 孔道壁面的共溶剂分子周围，在恒温加热的条件下提高泄压速率，由于压力降低将有大量的CO2解吸。随着泄压速率的增大三个样品反应器出口的CO2的流量逐渐增大，其反应器的出口平均流量分别为47、1140及17100 ml/min。在单位时间内，纳米孔道内聚集在共溶剂分子周围的CO2的解吸量也随之增大，可能导致吸附于载体表面的共溶剂分子脱附。因此，超临界下一定量的CO2快速解吸可成为吸附于载体表面的溶剂的一种反溶剂，使得其溶质无机盐在该过程中结晶析出。

Lee 等[40]采用离散化群体平衡模型（PBM）来描述SAS 粒径分布随超临界CO2流量变化的数学模型。在压力10 MPa，温度31.5℃，结晶持续时间60 s条件下，以CO2流量为自变量，以单位体积溶液内一定尺寸L到(L+dL)之间颗粒数量的n(t,L)群体密度为函数，研究SAS 过程的粒径分布规律。其模拟结果显示伴随反溶剂超临界CO2流量的增大（1、50 和100 ml/min），颗粒的平均粒径变小，而n(t,L)峰值的显著增加则说明颗粒数量也随之增多。而超临界沉积之后采用快速泄压的方案，在超临界下强化载体表面CO2脱附作用，伴随CO2流量的增加所制备的CuO NPs 的粒径分布规律以及孔道内NPs 的数量变化，均与这一模拟计算结果的变化规律相一致。

以泄压速率为18 MPa/min 的样品为研究对象，其反应器出口CO2平均流量已经达到17100 ml/min，而其所获得的CuO NPs 也已经降至（1.8 ± 0.6）nm。对于在超临界沉积之后利用CO2脱附作用调控负载型NPs 尺寸与分布的方法而言，伴随超临界下孔道内的CO2解吸量不断增加，如果颗粒数量会不断增加，则说明CO2脱附引起成核速率不断增大，作为成核驱动力的过饱和度也相应增加。根据Lee 等[40]的离散化PBM 推理可知，如果这一流量足够大，则可以如RESS 工艺，实现晶核与溶剂的快速分离，从而获得接近晶核尺寸的NPs，而本文的超临界沉积后的快速泄压方法的实验结果也确实在孔道内，获得了大量的1.5 nm 左右的接近晶核尺寸的NPs。说明本文所利用超临界CO2脱附作用，在纳米孔道内也同样具有实现晶核与溶剂快速分离的可能性。另外，在制备该样品重复实验中，一方面通过TEM 观察到CuO NPs 粒径分布可重复性好。另一方面，重复实验中各样品的Cu 担载量提升至12.3%，且重复实验中稳定在12%左右（三次重复实验Cu的担载量分别为12.0%、11.6%和12.5%）[39]。依据样品CuO-03 的Cu 担载量，换算为200 mg 载体质量的CuO 担载量为15.4%，其所负载的CuO 质量约为0.031 g。该样品的CuO NPs 平均粒径为1.8 nm，取0.9 nm 为NPs 球体的半径，其NPs 的体积为3.05 nm3。CuO 的密度为6.31 g/cm3，以1 mol 的CuO 质量估算其体积约为0.02 nm3。如此粒径1.8 nm 的CuO NPs 中约含有153 个CuO。同理，计算此样品中0.031 g 的CuO所对应其个数为2.3×1020，其中阿伏伽德罗常量为6.02×1023mol-1，这样换算为粒径1.8 nm 的NPs 的个数为1.5×1018。孔道内的成核时间取30 ns，氮气吸附测得载体SBA-15 孔容为0.99 cm3/g，对于200 mg SBA-15 载体其孔道容积为0.198 cm3，估算载体内的NPs成核速率为2.5×1026cm-3·s-1。

在RESS 工艺中在设备喷嘴内的成核速率的数量级能够达到1026cm-3·s-1[7]，与此前所估算的成核速率数量级一致，说明在纳米孔道内CO2脱附过程中能够实现共溶剂与溶质晶核的快速分离。为了进一步佐证该过程中对于SAS结晶过程可能性的分析，可将20 MPa、50℃下RESS 工艺中的过饱和度S引入作为参考，其值在Debenedetti 模型中在200 附近[5]，取S=200，且该压力下方程的修正系数K值随反应温度变化的波动较小，取其值为35[41]，来计算该过程中溶质的表面能σ和成核速率I。表面张力即表面能，二者是对同一表面现象的从不同角度（力学和热力学）的描述，量纲相同。依据前面1.2.1 节中的Debenedetti 模型，仍以此样品为研究对象，取临界晶核半径r*为0.5 nm，将其代入式（5），其中Cu(NO3)2的分子体积v1为1.34×10-28m3，将这一样品的Cu 担载量换算为在该压力、温度下80 ml 反应器中scCO2达到溶解平衡的溶质硝酸铜的摩尔分数2.76×10-4，计 算 得σ=0.03 J·m-2。样 品CuO-03 的200 mg SBA-15 的Cu 担载量为12.3%，将其转化为N值，即孔道内单位体积内的硝酸铜个数，N为1.17×1027m-3。以上数据代入式(6)，获得计算的成核速率I=3.02×1027cm-3·s-1。可见，如果将样品CuO-03 的实验数据代入RESS 工艺的Debenedetti 模型所获得成核速率的数量级与按其样品Cu 担载量所估算的成核速率I数量级是相接近的。同样，也可将以上数据代入Türk 模型做成核速率的估算。如1.2.2 节中式（7）所示，临界晶核半径r*为0.5 nm，计算σ=0.04 J/m2。将其代入式（8），其中ρM为混合物密度，其物理意义为单位体积内的溶质分子个数，数值仍为1.17×1027m-3。求得K0=7.70×1028cm-3·s-1，成核速率I=3.69×1025cm-3·s-1，也与估算的成核速率数量级相接近。

对于SAS 的群体密度函数n，由式（10）和式（11）可知，由于此样品的颗粒直径LP已经接近1 nm，则n接近PBM 的边界条件no晶核群体密度函数。如式（12）所示，成核速率B为初级成核速率B'和二次成核速率B″之和，考虑到样品CuO-03 载体孔道内所获得的颗粒粒径接近晶核尺寸，分析B主要由初级成核所决定，B'的表达式如式（13）～式(15)所示[23,40,42]。

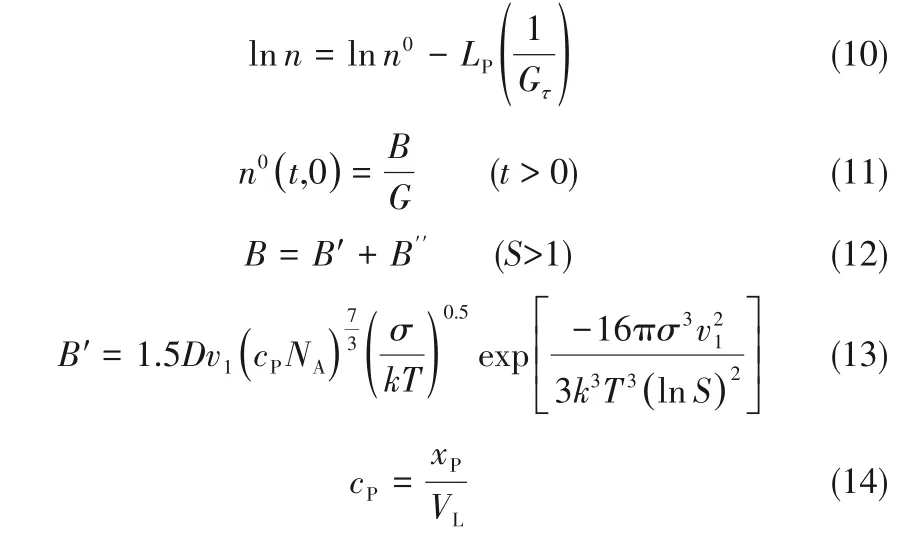
式中，τ是液相溶液滞留时间，s；cP是溶质浓度，mol/m3；xP是溶质的物质的量，mol；VL是液相体积，m3；D是溶质在液相溶剂中的扩散系数，m2/s；η是溶剂黏度，Pa·s；r是溶质分子的半径，m。

同样可将以上数据代入式（13）～式（15），计算SAS过程中的成核速率B'。由于式中成核动力仍为lnS，因此颗粒晶体的表面能σ仍为0.04 J/m2，过饱和度S取200，样品前驱物剂量为200 mg，换算为xP为8.26×10-4mol，溶剂体积(1.0 ml 乙二醇+0.5 ml 水)约为1.5 ml，溶质浓度cP为5.51×102mol/m3。溶剂黏度η取EG 和DIW 常温下黏度的平均值为1.33×10-2Pa·s，假设溶质分子为球形，硝酸铜分子体积为ν1为1.34×10-28m3，其半径r为3.18×10-10m 代入式（15）即Stokes-Einstein(S-E)方程，求得D为5.58×10-11m2/s。将以上数据代入式（13）计算B'为3.66×1025cm-3·s-1，同样接近所估算的成核速率的数量级。可见，在超临界沉积之后CO2的快速解吸，能使得SBA-15孔道内获得了极高的成核速率。在如此高成核速率下仍能获得高分散的接近晶核尺寸的NPs，则说明由于快速降压，载体表面大量CO2脱附，其反溶剂效应实现了近似于RESS 工艺的溶剂与溶质晶核的快速分离，从而抑制了NPs在孔道内生长。

值得注意的是，依据晶体成核的数学模型，计算出的晶体表面能σ分别为0.03 和0.04 J/m2，而通常无机固体和金属的表面能大于0.1 J/m2。Waychunas 等[43]利用小角度X 射线散射（small-angle X-ray scattering，SAXS）技术，原位探测了溶液在石英表面上的CaCO3非均相成核现象，发现实验测算其有效表面能σ'（0.036 J/m2）要低于其均相成核的表面能σ（≈0.12 J/m2），即在石英表面上的CaCO3成核能垒被降低，所以非均相成核可以在比均相成核低的过饱和度下发生。本文所计算的纳米孔道内颗粒的表面能σ小于0.1 J/m2，而如果σ取为0.1 J/m2（lnS=12），则成核速率为5.86×1018cm-3·s-1，显著低于根据样品Cu 担载量以及RESS 和SAS 成核模型所估算的成核速率数量级（1025～26cm-3·s-1）。这说明在超临界沉积后，快速降压导致的CO2脱附作用在实现溶剂与溶质快速分离的同时，其成核路径为吸附于SBA-15 孔道表面的硝酸铜的非均相成核过程。

3 结 论

本文通过CNT 模型的三维响应面，分析物质的表面张力、温度以及过饱和度三者间交互作用对于结晶成核速率的影响。其中过饱和度作为成核的驱动力，而物质表面张力即其成核能垒的高低对于溶液成核速率的影响则尤为显著。通过RESS 和SAS 工艺成核模型与CNT 模型的比较，分析超临界流体作为溶剂，其非理想性对于成核速率的影响，从成核路径角度分析了超临界流体调控晶体尺寸的机理。利用超临界沉积法中的泄压过程，调控泄压速率获得了负载不同平均粒径的CuO NPs的复合材料，通过其金属担载量估算载体孔道内的成核速率的数量级达到1026cm-3·s-1，其TEM 图中的SBA-15 孔道内所对应的NPs 平均粒径也接近晶核尺寸约为1.8 nm。表明超临界CO2脱附作用使溶质硝酸铜在获得了极高成核速率的同时，实现溶质与溶剂的快速分离，而后在复合材料的焙烧阶段形成高分散且数量众多的NPs。依据离散化PBM 模型SAS工艺的边界条件，将复合材料的载体质量、载体孔容及金属担载量等信息代入方程，计算其孔道内成核速率数量级达到1025cm-3·s-1。分析伴随泄压速率的提升溶质成核速率增大，孔道内的NPs 平均粒径随之减小。这与离散化PBM 模型模拟SAS 工艺中，伴随CO2流量增加而NPs 平均粒径减小的变化规律相一致。因此，本文为分析微观尺度下SAS 过程的实现提供了实验与理论基础。