基于ABAQUS 的某型号轿车连杆拓扑优化设计

朱鑫垚，赵宇，李彦

（200093 上海市 上海理工大学 机械工程学院）

0 引言

2009 年以来,我国汽车产销量已经连续11年位居世界首位。国家不断加大对汽车行业的扶持，促进汽车行业向智能化与网联化的方向发展，让我国有望在新一轮全球汽车行业竞争中实现跨越式发展[1]。为了能达到这一发展目标，需要汽车行业采用足够智能化与功能强大的仿真设计软件来实现这一宏伟目标。其中ABAQUS 软件有着强大的计算功能，是十分理想的设计与仿真软件，能够为企业使用者或者个人使用者提供完整的分析途径，目前已经大量应用于汽车领域，能为使用者们提供有效的优化设计方案。

根据相关研究显示，连杆进行相关优化可以降低连杆质量并能有效降低生产成本[2]。基于ABAQUS 软件的拓扑优化技术能够在不影响汽车相关性能的前提下，减轻汽车质量进而降低生产成本，能够为汽车企业带来可观的经济效益。

1 零件建模

连杆是汽车发动机中常见的零件，其作用是连接活塞和曲轴，并将转矩由活塞传递给曲轴。在工作时连杆会受交变载荷的影响，是发动机的重要受力部件，主要受力表现为拉伸及压缩[3]。连杆受力情况与其本身质量呈现一定比例关系，对其进行轻量化，不仅可以降低机械损失，提高发动机效率，还可以减少转动惯量，进而能够改善发动机的噪音问题[4]。连杆的设计已经十分成熟，其轻量化主要是通过所用材料和相关制造工艺来实现。连杆的制造工艺为铸造，因为铸造的成本较低，且生产过程容易掌控。连杆材料选择调质钢35CrMo，调质钢35CrMo 有良好综合机械性能，同时具有较好的韧性和塑性，是制造发动机连杆十分理想的材料，其力学性质如表1 所示。

表1 35CrMo 力学性能Tab.1 Mechanical properties of 35CrMo

首先在SolidWorks 中建立某型号轿车连杆三维模型，如图1 所示。

图1 轿车连杆三维模型Fig.1 3D model of car connecting rod

2 有限元分析

2.1 有限元模型的建立

有限元法（FEM，Finite Element Method）利用许多简单、连续、相互作用的单元去逼近无限未知量的真实系统。基本原理是将单元中的节点进行计算，得出系统离散域总装方程组，并求解出总装方程，求解结果即节点处状态变量的近似值。但在实际分析过程中有很大局限性，需要利用有限元软件将分析对象网格化，网格化的实质是将连续体看作数量有限的节点和单元的组合体，即将其从单纯的物理模型变为网格化的有限元模型，进而对结构复杂物体进行相关分析。

本次分析对象为某型号轿车连杆，连杆本身存在许多圆角及过渡圆弧，网格划分的处理细节较多，会导致划分网格种类不一，从而加大本身的计算量和复杂程度，所以也会对所需计算机配置提出更高的要求。对连杆结构进行合适的网格划分，对后面计算分析的准确性和可行性有重要作用。

为了得到与实际结果接近的计算分析结果，采用自由网格划分方法。划分的网格大小为8，采用二次线性四面体单元自由划分方法。网格划分结果如图2 所示，共计19 407 个单元。

图2 轿车连杆网格细化图Fig.2 Element refinement of car connecting rod

2.2 施加载荷

曲柄连杆机构在发动机中的作用是传递动力和运动方向，整个发动机动力输出则是通过燃料燃烧产生的气体压力通过连杆作用给曲轴，并最终由飞轮输出来实现，故曲柄连杆机构的受力情况较为复杂。汽车发动机在正常工作时，是做有规律的周期性运动，活塞组件内的燃烧室产生的气体交变施加在连杆上。曲轴上的飞轮组高速转动，使得整个活塞组的惯性力较大，其惯性力来源于活塞组及杆件自身，但在分析时考虑主要因素即可，即对连杆做静力分析[5]。连杆在正常工作时，小头孔与其配合件摩擦较小，可以忽略不计，故可将连杆看作二力杆，受拉力与压力[6]。由于小头孔内接触面积小，可将动力学转化为静力学问题来进行求解。进行分析时考虑最恶劣的压缩工况进行分析[7]。

根据气体压力相关公式[8]

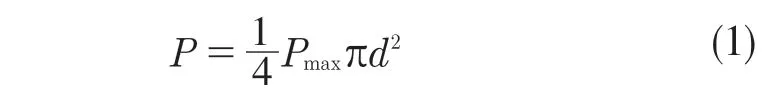
式中：Pmax——气缸内燃气最大爆发压力；d——气缸直径；P——连杆轴向力。通过相关分析计算，燃气的最大爆发压力约为4 MPa，对应的轴向力约为14 550 N。如图3 所示，连杆小头孔受到Y轴方向14 550 N 的压力。

图3 轿车连杆受压图Fig.3 Compression diagram of connecting rod of car

2.3 施加边界条件

在进行相关静力学分析时，需要对其进行自由度的约束。连杆的大头孔与曲轴一同旋转，小头孔与活塞销链接。在ABAQUS 分析中可以将其看作MPC 约束（Multi-Point Constraints）。MPC定义的是一种节点自由度的耦合关系，将其中一个节点的某几个自由度看作标准值，然后让其他节点的某几个自由度与这种标准值建立关系，这种关系可以用来表达一些特殊的现象，例如滑动连接。因此，连杆小头孔和大头孔采用MPC 约束里的梁约束，并将大头孔自由度完全约束，如图4 所示，为施加边界条件图。

图4 施加边界条件Fig.4 Imposing boundary conditions

2.4 分析结果

对连杆进行静力学分析计算可得结果如图5、图6 所示，应力最大值为1.969 MPa，位移最大值为0.058 2 mm。

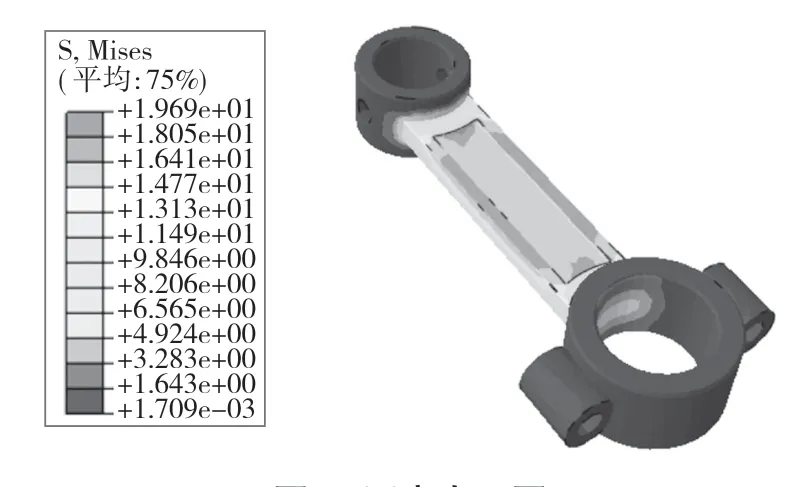
图5 压应力云图Fig.5 Compressive stress results

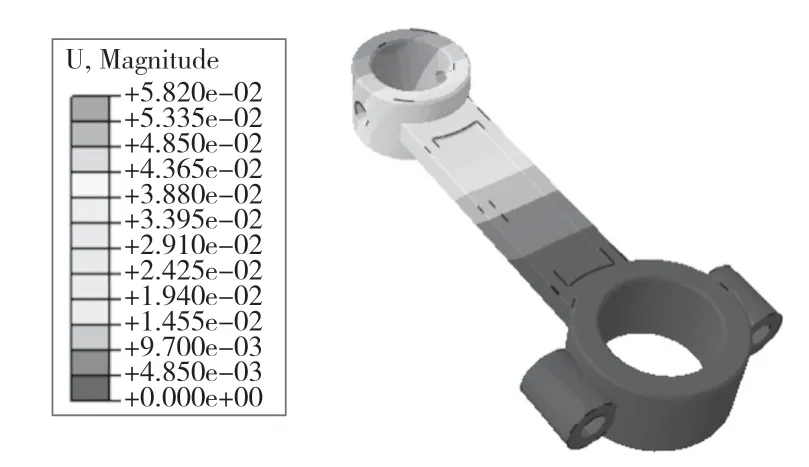
图6 位移云图Fig.6 Displacement results

3 拓扑优化设计

3.1 优化过程

本次拓扑优化的对象是某型号轿车连杆，其优化过程如图7 所示。

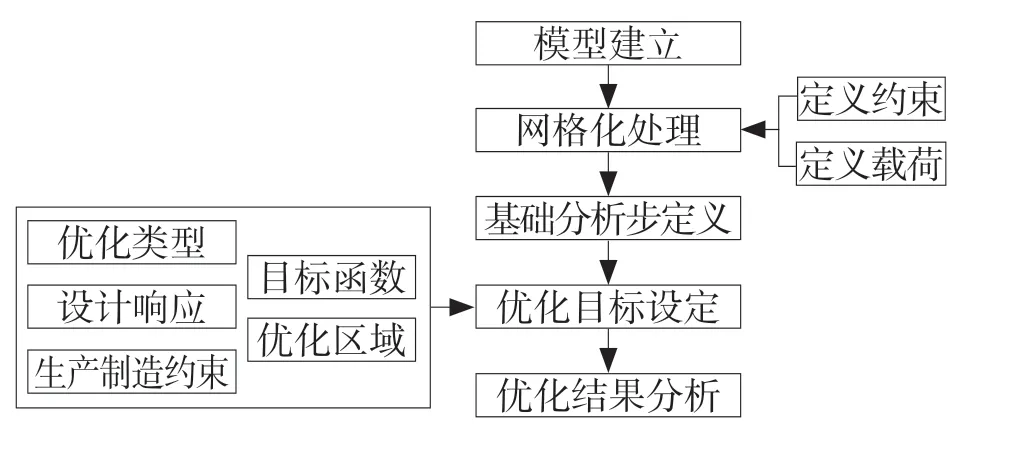
图7 优化过程流程图Fig.7 Flow chart of optimization process

拓扑优化常用的方法有变密度法、均匀化法和水平集法，其中应用最广的是变密度法。变密度法可以用式（2）[9]：

式中：Xi——设计变量；n——变量个数；K——总刚度矩阵；U——模型位移向量；F——模型所受的外力向量；V——模型体积；V*——模型拓扑优化后的体积峰值。

本次优化对连杆杆身进行优化，大小头孔尺寸及结构保持不变，如图8 所示为设计区域，设计变量为单元密度，采用变密度法。设定拓扑优化后的设计区域的体积不超过优化前设计区域体积的25%，且最大应力不超过调质钢35CrMo 的屈服强度极限835 MPa，并增加生产制造约束使得拓扑出来的新结构有加工可行性。

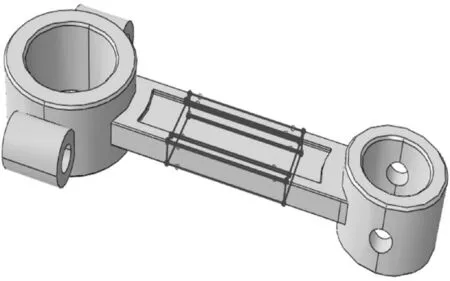
图8 设计区域Fig.8 Design area

3.2 优化结果

优化后结果如图9 所示。模型经过31 次迭代运算后收敛且应变能最小。体积比变化曲线如图10 所示，设计区域体积比约为0.25，即连杆优化模型在设计区域能比原始模型节省大约75%的材料。

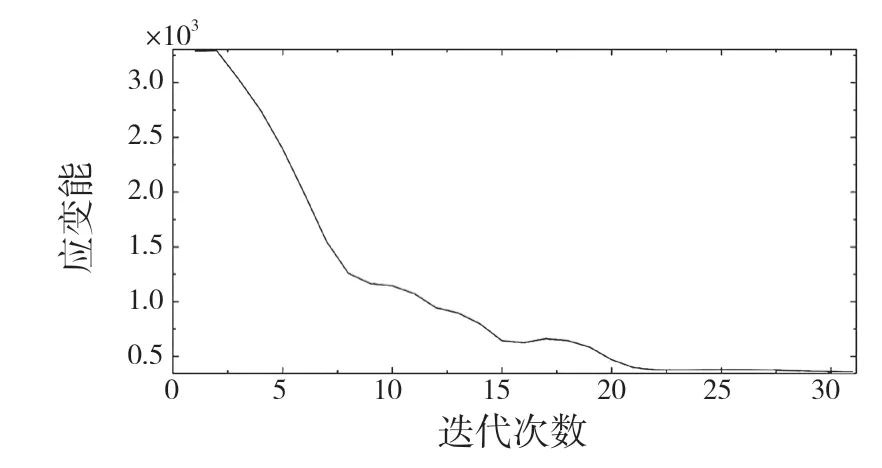
图9 模型迭代次数曲线Fig.9 Model iteration times curve

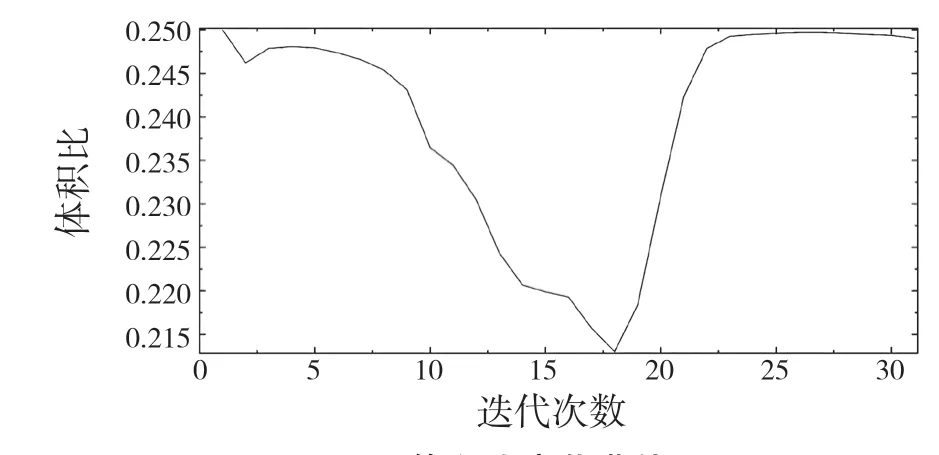
图10 体积比变化曲线Fig.10 Change curve of volume ratio

提取第31 次优化的应力云图和位移云图如图11、图12 所示。可以发现材料减少的区域为杆身中间位置，由于施加生产制造约束，所以去除多余质量后的结构在机加工工艺上能够实现。

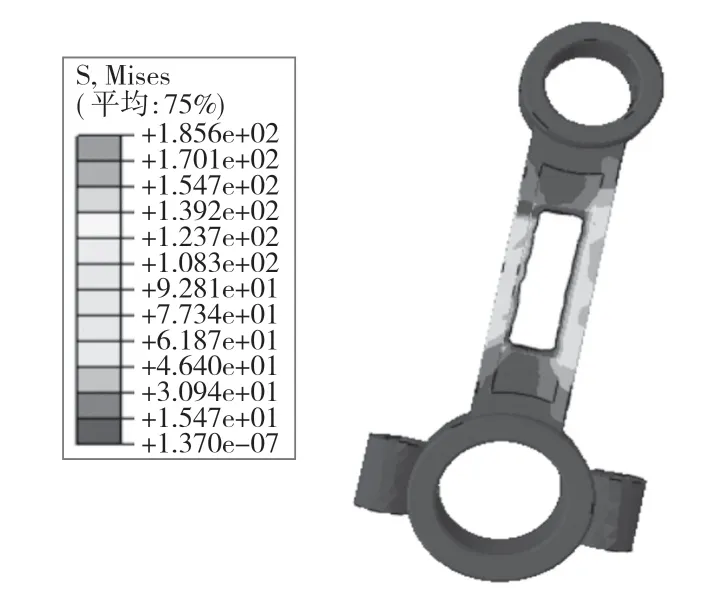
图11 连杆优化模型应力云图Fig.11 Stress of connecting rod optimization model

图12 连杆优化模型位移云图Fig.12 Displacement of optimal model of connecting rod

优化前后结果见表2，优化后的结构最大应力185.6 MPa，远小于35CrMo 的屈服强度极限835 MPa，属于安全范围之内。图12 得出优化后最大位移为0.062 33 mm,与连杆原始模型最大位移0.058 20 mm 相比变化不大。

表2 优化前后结果Tab.2 Results before and after optimization

4 结语

在ABAQUS 软件基础上对某型号轿车连杆进行了最恶劣工况压缩条件下的静力学分析，并在此基础上进行拓扑优化设计。从最终结果可以看出，杆身设计区域去除质量较多，且满足实际机械加工工艺要求，对降低连杆自身质量和成本有较大意义，为某型号轿车连杆优化提供了一种可行的优化方法。此方法能够帮助企业相关人员对产品进行符合要求的优化设计，对产品的更新换代和提升企业核心竞争力有着重要作用。