晶圆传输平台轨迹规划与控制算法研究

董乐，宋芳

（201620 上海市 上海工程技术大学）

0 引言

在集成电路制造过程中，晶圆需要在各工位之间频繁传输，晶圆传输机器人保证了晶圆在各工位之间精确、快速、平稳地传输，因此晶圆传输机器人的研制对集成电路产业的发展至关重要[1-4]。在相关研究中，Chen[5]等通过加快晶圆定位过程，提高了晶圆传输效率；刘小磊[6]采用时间最优轨迹实现了晶圆传输机器人的快速平稳传输。由于真空中只能通过摩擦式晶圆传输机械手对晶圆进行传输，晶圆传输效率与摩擦力息息相关。申磊[7]提出了一种基于微摩擦矩阵的方法来提高晶圆传输过程中的加速度；蔡昌宗[8]在申磊的基础上提出了一种基于位姿调整的加速度算法，突破了摩擦力限制，大大提高了晶圆传输效率。Liu[9]等对晶圆传输过程中的传输速度与机架振动进行了分析，采用了轨迹规划方法对振动进行了抑制，提高了传输效率。由于常规的PD 控制算法在干扰存在情况下不能取得很好的控制效果，造成传输精度差，影响晶圆传输效率。任鹏飞[10]、贺军[11]等分别采用RBF 神经网络和模糊控制算法解决模型不确定性和负载变化对系统的影响；胡勇[12]通过设计鲁棒控制算法，减小传输过程中的干扰，实现了晶圆稳定高效传输；He[13]等建立了四自由度的晶圆传输机器人模型，并对其进行了解耦伺服控制，提高了晶圆传输机器人的动态跟踪性能。

本文在位姿调整算法的基础上，充分考虑最大加速度与位姿角的关系后，对晶圆传输轨迹进行重新规划，避免相对滑动。考虑晶圆传输平台的非线性、不确定性、关节耦合对轨迹跟踪控制及传输效率的不利影响，通过线性反馈化解耦算法以及干扰观测器实现控制系统的解耦控制，并设计积分滑模控制保证控制性能，提高系统鲁棒性。

1 晶圆传输实验平台

1.1 平台构成

根据实验要求，项目组搭建了基于位姿调整的二自由度晶圆传输机器人实验平台，如图1 所示。实验平台动力系统由一个直线电机和一个旋转电机组成，为方便描述，将直线电机所在的轴命名为轴1，另一个轴为轴2。

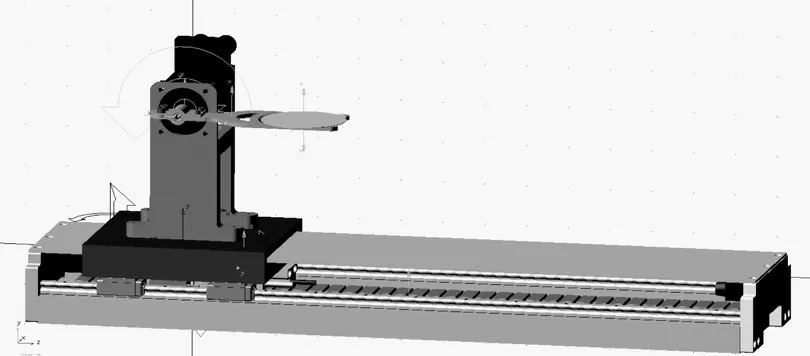
图1 晶圆传输实验平台Fig.1 Wafer transmission experimental platform

1.2 受力分析

在实验平台的运动过程中，加速度、速度曲线是对称的，除受力方向外，晶圆在各运动阶段中的力学状态是相似的，因此只需要对初始加速阶段进行力学分析，就可以类比得到其他阶段运动过程中的受力状态。

对图2 状态进行受力分析。图2 中，m 为晶圆质量；g 为重力加速度；a 为平台运动的加速度；Fn为微结构对晶圆的支持力；w，r 分别为末端执行器旋转的角速度和半径；f 为微结构与晶圆间的摩擦力；Fr为向心力。采用经典的摩擦理论，取最大静摩擦力近似等于滑动摩擦力。根据达朗贝尔原理[14]得

图2 晶圆受力图Fig.2 Force diagram of a wafer

由于摩擦力的方向不确定，微结构与晶圆间的摩擦为

忽略运动过程中的微结构形变，计算得到等效摩擦系数μ=0.447。由式（1）与式（2）可得

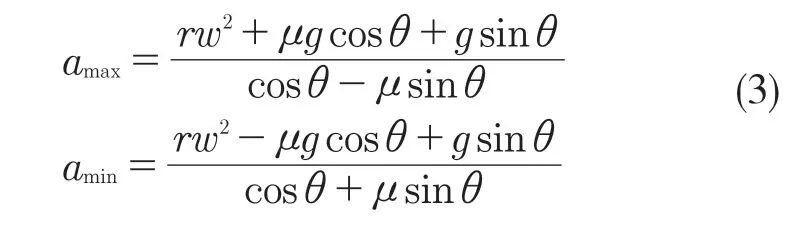
式中：amax——最大加速度；amin——最小加速度。

在实际运行过程中，由式（3）可以看出向心力的存在可以增大加速度，由于末端执行器旋转到一定角度后进行平动，此时不存在向心力，因此考虑向心力存在与不存在两种情况。取最大加速度中的小值，最小加速度中的较大值，得到加速度与旋转角度之间的关系如图3 所示。

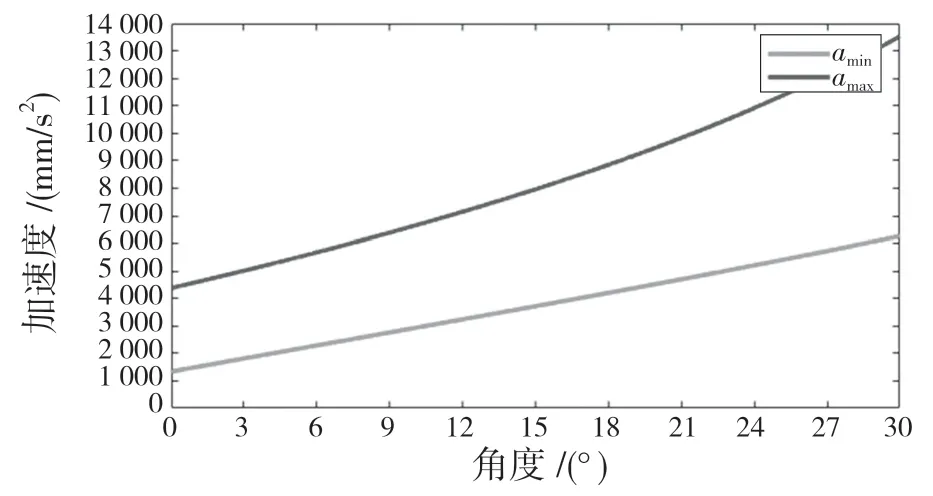
图3 加速度与角度关系图Fig.3 Relationship between acceleration and angle

根据平台性能以及加速度和角速度的关系，可以求得平台运动过程中的最大加速度。采用基于位姿调整的S 加速算法[8]，得到各轴的位移、速度、加速度轨迹如图4 和图5 所示。

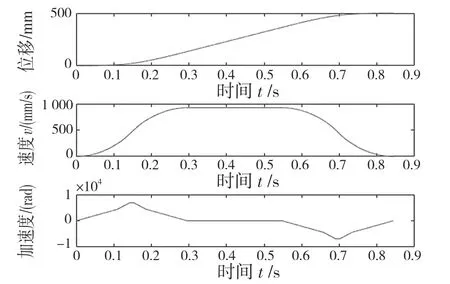
图4 轴1 轨迹Fig.4 Trajectory of axis 1

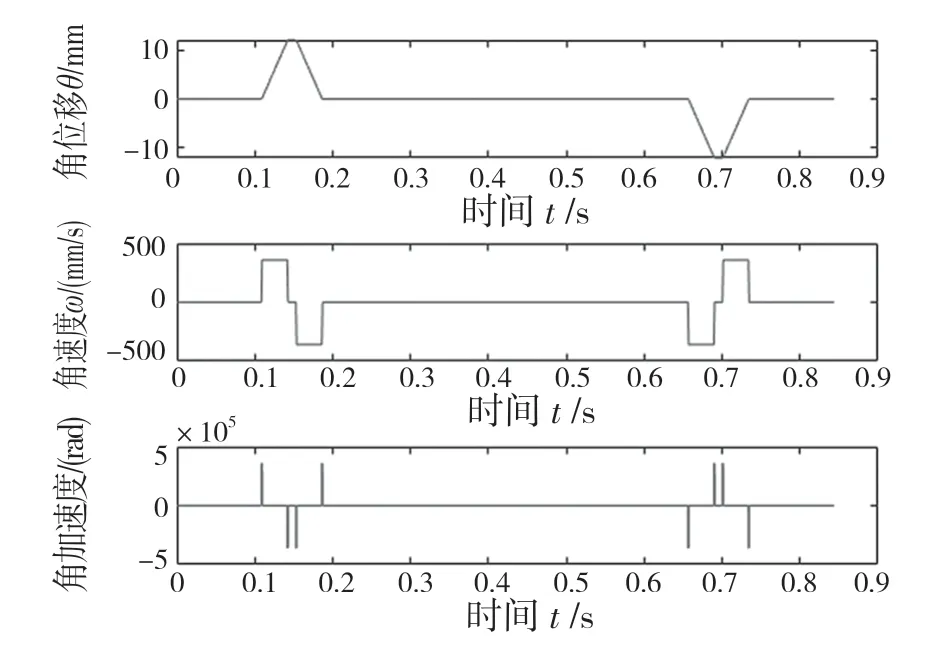
图5 轴2 轨迹Fig.5 Trajectory of axis 2

在ADAMS 环境下，对规划轨迹进行仿真，晶圆与末端执行器位移如图6 所示。由图中可以看出晶圆与末端执行器没有相对滑动。

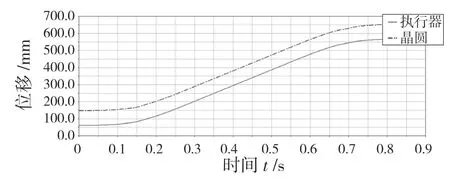
图6 末端执行器与晶圆轨迹Fig.6 End-effector and wafer trajectory

2 动力学模型建立

运用拉格朗日法建立晶圆传输平台的动力学方程得

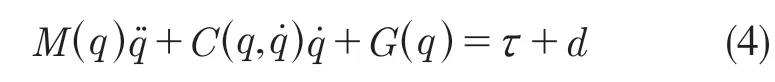
式中：d——不确定的干扰；q——关节位移；τ——关节输入力或力矩。由于实际中各种干扰的存在，很难获得机器人模型的完整信息，只能获得机器人的名义模型。将机器人未建模动态当作干扰，则式（4）变为

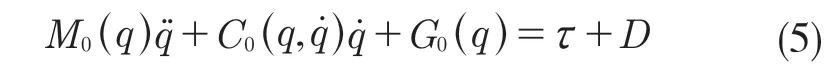
式中：M0（q），C（0q，），G0（q）——名义模型参数；D——包含模型误差的总的不确定项。

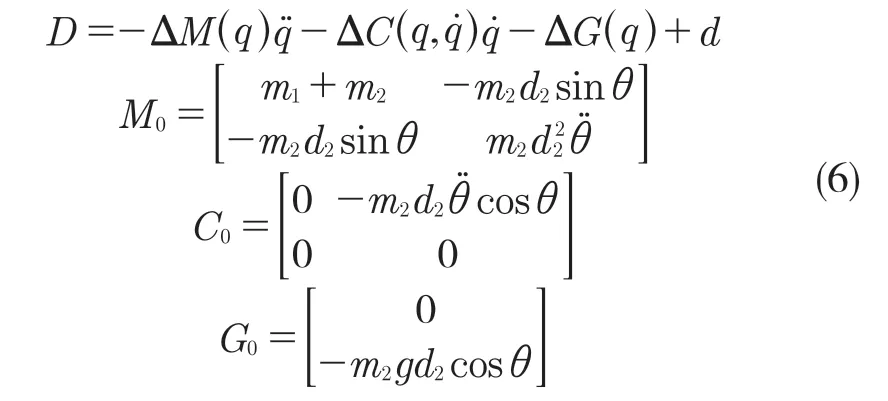
式中：m1——旋转电机、电机支架和底座的总质量；m2——末端执行器和晶圆的总质量；d2——末端执行器质心到旋转中心距离；θ——轴2 旋转角度；g——重力加速度。

3 控制器设计

3.1 线性反馈化解耦

由于晶圆传输平台是一个非线性强耦合系统，传统PD 控制并不能很好满足平台控制性能的要求，本文采用反馈线性化解耦思想，利用干扰观测器对系统不确定性进行实时补偿，并通过积分滑模控制器消除观测误差增强系统鲁棒性。

根据式（5）设计控制律

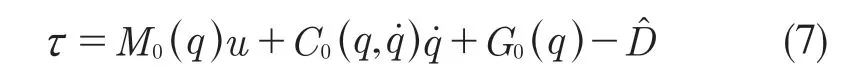
式中：u——虚拟控制量，通过合理设计u 可以提高系统动态品质。

将式（7）代入式（5）化简可得

3.2 干扰观测器

根据估计干扰的输出值与实际干扰的差值对估计值进行实时修正，则干扰观测器可设计为

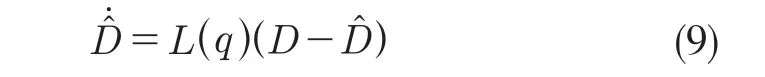
其中L(q)>0，定义辅助状态变量[15-16]：

对式（10）中的Z 进行微分，联立式（6）、式（9）、式（10）、式（11），得到新的干扰观测器表达式为

令观测误差为=D-，一般没有干扰D的微分先验经验，假设D 的变化相对于干扰器的动态是缓慢的，可以取D˙=0，对观测误差求导可得

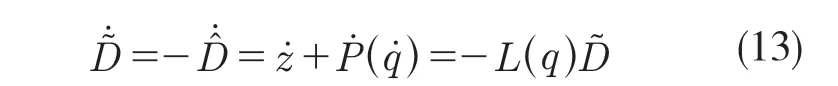
式中：X——常数矩阵且可逆。取观测器Lyapunov 函数为

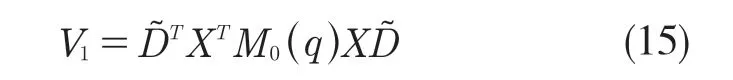
由于M（q）>0，所以V1是正定的。对V1求导，结合式（10）可得：

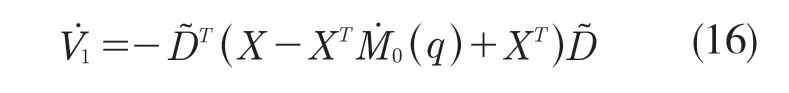
构造不等式

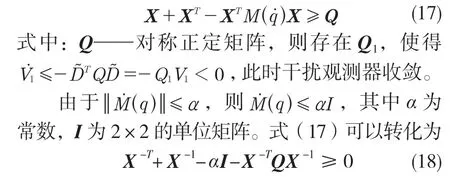
根据舒尔补定理，式（18）等价为

此时可利用线性矩阵不等式的方法求解X-1，便可以得到L（q）与P（）的表达式。

3.2 积分滑模控制

滑模控制是一种非线性的控制算法，由于对控制对象内部参数变化和外部扰动的不敏感、快速响应、物理实现简单等优点得到了广泛应用。定义跟踪误差为E=-，采用积分滑模面来保证系统初始状态时就位于滑模面上，可以有效减小系统抖振现象。对式（8）进行控制算法设计，定义积分滑模面为

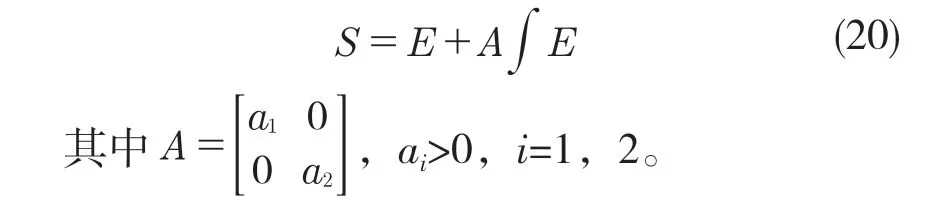
采用指数趋近率方法设计控制器，对式（20）进行微分，得：

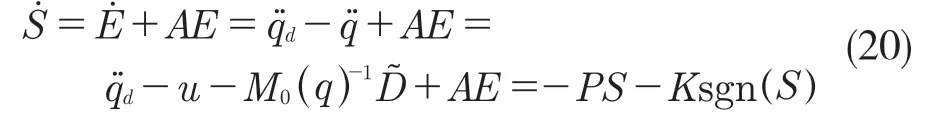
假设干扰观测器误差为0，则

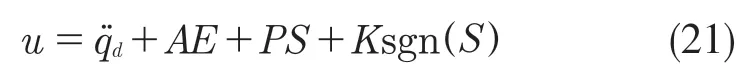
4 仿真实验及分析

本文设计的晶圆传输平台参数为m1=24 kg、m2=0.3 kg，d2=0.07 m。在SolidWorks 中建立晶圆传输平台的三维模型，并在ADAMS 中建立控制系统模型导入Simulink，通过S 函数实现基于干扰观测器的积分滑模和线性化反馈控制。

经过试验滑模控制器参数为

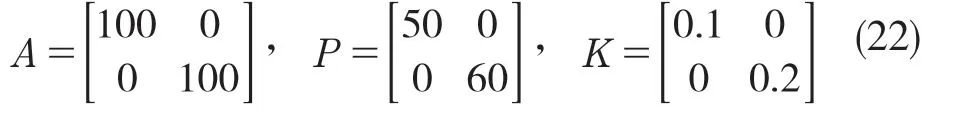
为了减小系统抖振，用饱和函数代替符号函数，取边界层厚度为0.001。

干扰观测器仿真结果如图7 所示。由图中可以看出，干扰观测器可以较好地跟踪实际误差，通过干扰观测器对不确定干扰进行实时补偿，采用线性化反馈化方法对晶圆传输平台进行解耦控制，利用积分滑模控制保障系统性能并消除观测误差影响，晶圆传输平台轨迹跟踪结果如图8 和图9，此算法在模型不确定情况下对规划轨迹有较好的规划效果。

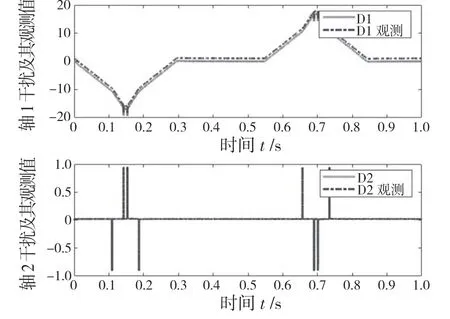
图7 观测干扰与实际干扰Fig.7 Observation interference and actual interference

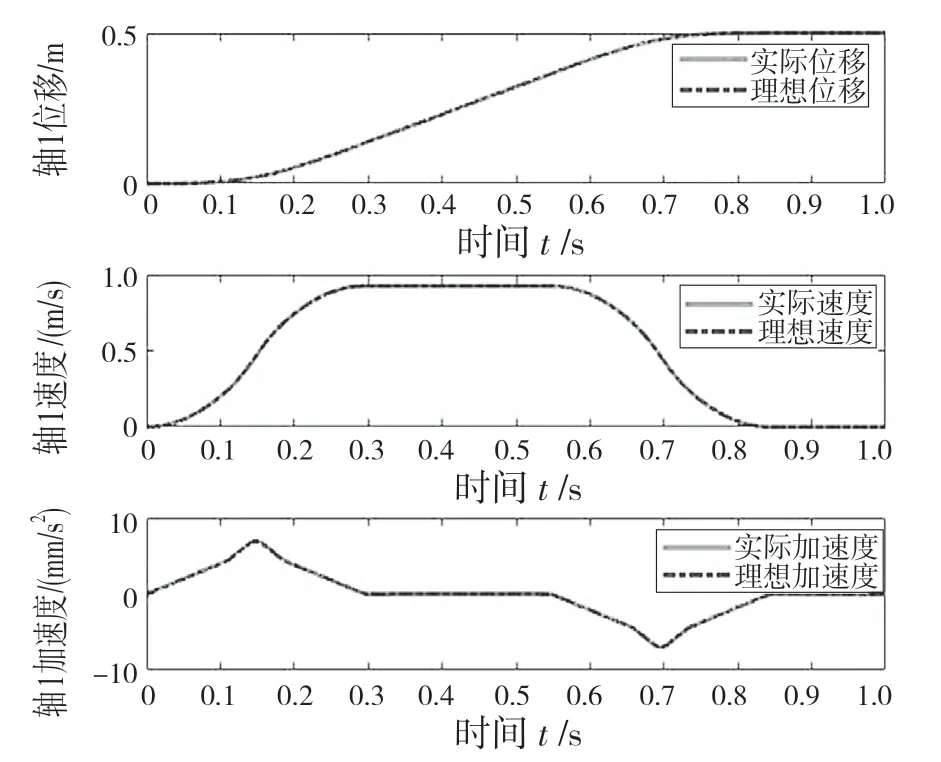
图8 轴1 轨迹跟踪Fig.8 Track of axis 1

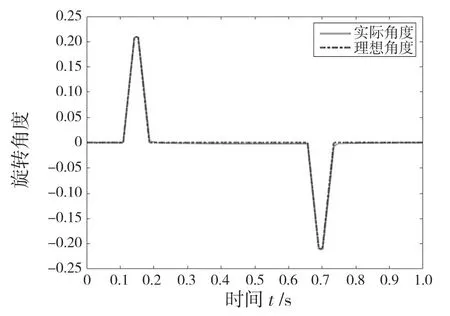
图9 轴2 旋转角度Fig.9 Axis 2 rotation angle

5 总结

本文在晶圆传输机器人末端位姿调整的算法基础上搭建了实验平台，通过对平台分析得到了晶圆传输最大加速度与末端位姿角的关系，规划了晶圆传输平台运动轨迹，并通过晶圆传输平台名义模型，设计了基于观测干扰器的线性化解耦控制算法，通过积分滑模控制来保证系统动态品质，仿真实验表明，此算法在模型不确定情况下有较好的跟踪精度，可以有效提高晶圆传输效率。