基于EMD-GPR 的锂离子电池剩余寿命预测方法研究

李泱，张营，邹博雨，陈璐，徐剑澜，顾杰

（210037 江苏省 南京市 南京林业大学 汽车与交通工程学院）

0 引言

锂离子电池剩余寿命（Remaining Useful Life，RUL）预测方法的研究，对应用锂电池各领域[1]的安全性、经济性和稳定性都起着关键作用。目前锂电池剩余寿命预测的方法主要有3 种：基于经验的方法、基于模型的方法和数据驱动的方法。其中基于数据驱动的方法不依赖于电池的内部结构，用表征性能退化的特征参数建立模型，获取退化的规律[2]。常见基于数据驱动的RUL 预测方法主要有：自回归[3]、人工神经网络[4-5]、支持向量机[6-7]、高斯过程回归（GPR）[8-9]、相关向量机[10]等。其中，GPR 以贝叶斯框架为理论基础，由于其训练易于实现、泛化能力强和善于处理非线性问题的优点，被广泛应用于回归和分类问题中[11]。庞景月[8]利用高斯过程回归方法给出锂电池剩余寿命预测的不确定性区间，构建了在线剩余寿命预测的方法；吴祎[9]提出一种基于变分模态分解和高斯过程回归的锂离子电池剩余寿命预测方法，降低了容量预测误差。

大多数研究直接采用电池容量数据或将电池容量数据分解预测后再进行加和处理，而锂电池性能退化数据不仅包含整体性能退化信息，同时包括因电池搁置引起的容量再生分量以及随环境因素变化的波动量，导致电池性能退化过程呈现非线性和时变性[9]。而EMD 分解后的趋势项可以完整、平滑地表征电池退化趋势，能够有效提高GPR模型预测寿命的精度。基于上述现状分析，本文提出一种基于EMD 和GPR 的锂离子电池剩余寿命预测方法。

1 经验模态分解（EMD）

经验模态分解（EMD）[12]将信号分解成若干个本征模态函数（IMF）和一个原始信号的趋势项，每个分量包含着不同的局部特征。设数据信号为x(t)，EMD 分解步骤[13]如下：

步骤1：标记出x（t）所有局部极大值点和极小值点，然后使用3 次样条插值法分别拟合得到原始数据信号的上包络线E1（t）和下包络线E2（t），计算上下包络线的平均值曲线m1（t）：

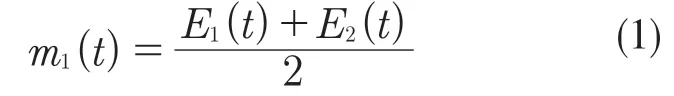
步骤2：原始数据信号x（t）减去上下包络线的平均值m1(t)得到一个新的数据信号h1(t)：

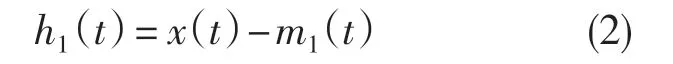
步骤3：判断新的数据信号h1（t）是否满足IMF 的条件，若h1（t）不是一个IMF，则将h1（t）的上下包络线的平均值曲线定义为m11（t），将h1（t）减去m11（t），得到h11（t）：

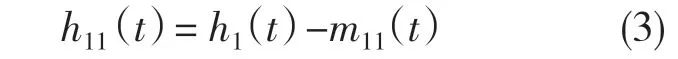
重复式（3）k 次，有：

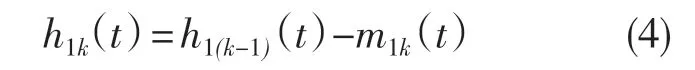
式中：h1k（t）——第k 次分解得到的信号；h1（k-1）（t）——第k-1 次分解得到的信号；m1k（t）——h1k（t）的平均包络线，当满足IMF 条件时，h1k（t）变为第1 个IMF 分量，记为f1（t）。

步骤4：用原始数据信号x（t）减去f1（t）得到一个残余量信号r1（t）：

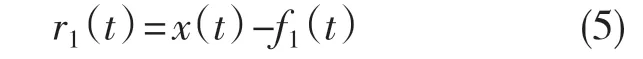
将残余量信号r1（t）看作是新的数据信号x（t），重复上述步骤，可依次得到f1（t），f2（t），L。当rn（t）变成常量或者单调函数时，EMD 分解结束，此时rn（t）称为趋势项，它表示原始数据信号的总体趋势。即原始数据信号x（t）可表示为一组IMF分量和一个趋势项的和：

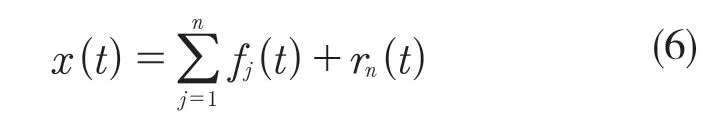
2 基于EMD-GPR 的锂离子电池剩余寿命预测方法

高斯过程回归（Gaussian Process Regression，GPR）模型是非参数的基于内核的概率模型，高斯过程回归相较于其他数据驱动方法可在得到输出参数的同时获得预测的置信区间，给调用者提供更多参考资料，数据范围的扩展也增强了预测结果的有效性[14]。

本文提出的是一种基于EMD 和GPR 的锂离子电池剩余寿命预测方法。首先，利用EMD 分解锂电池容量信号，得到特征尺度各不相同的特征分量；接着基于趋势项，训练GPR 模型；最后，利用拟合的GPR 模型分别对锂离子电池剩余寿命进行点预测和区间预测，并对2 种预测方法进行比较分析。其流程如图1 所示，具体包括如下步骤：

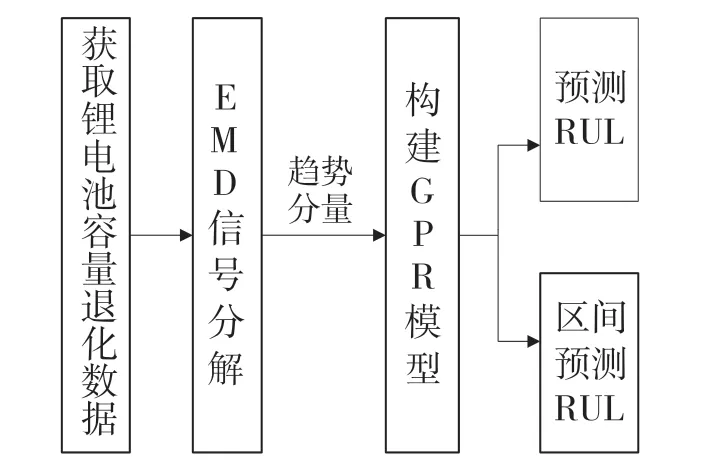
图1 基于EMD-GPR 的锂电池剩余寿命预测流程图Fig.1 Flow chart of residual life prediction of lithium batteries based on EMD-GPR

步骤1：获取锂离子电池容量退化数据，以T 周期作为预测起始点，基于1-T 周期的数据进行模型训练，以T 周期之后的数据验证预测模型；

步骤2：采用EMD 对原始容量数据1-T 周期进行分解，得到电池容量退化趋势分量；

步骤3：基于EMD 分解的趋势项，选择马特恩函数内核函数构建GPR 预测模型；

步骤4：利用拟合的GPR 模型分别对锂离子电池剩余寿命进行点预测和区间预测；

步骤5：以T 周期之后的数据验证预测模型，并对结果进行比较分析。

3 实验分析

本文采用美国国家航空航天局（National Aeronautics and Space Administration,NASA）所提供的锂离子电池实验数据集1 中4 个电池的实验数据[15]。数据集中对于给定的放电周期数据，NASA 表示可以用来预测电池的剩余寿命或剩余电荷，可见数据的采用是合理的。电池容量退化曲线如图2 所示。可以发现4 种电池容量的大体退化趋势相同，都随着循环次数的增加而减小，呈现非线性的波动下降的趋势，且在下降的过程中都存在着容量再生阶段。

本文以电池B0005 为例，对所提预测方法进行分析和验证。图3 为电池B0005 经过EMD 分解后的效果图。由图3 可以发现，趋势项可以反映出电池退化的整体趋势，且与图2 中完整电池容量退化过程近似，而IMF1-IMF4 反映容量退化过程中的波动量，这表明采用EMD 可有效解耦容量退化信号中的不同信息分量，并有效降低信号的复杂性和非平稳性。

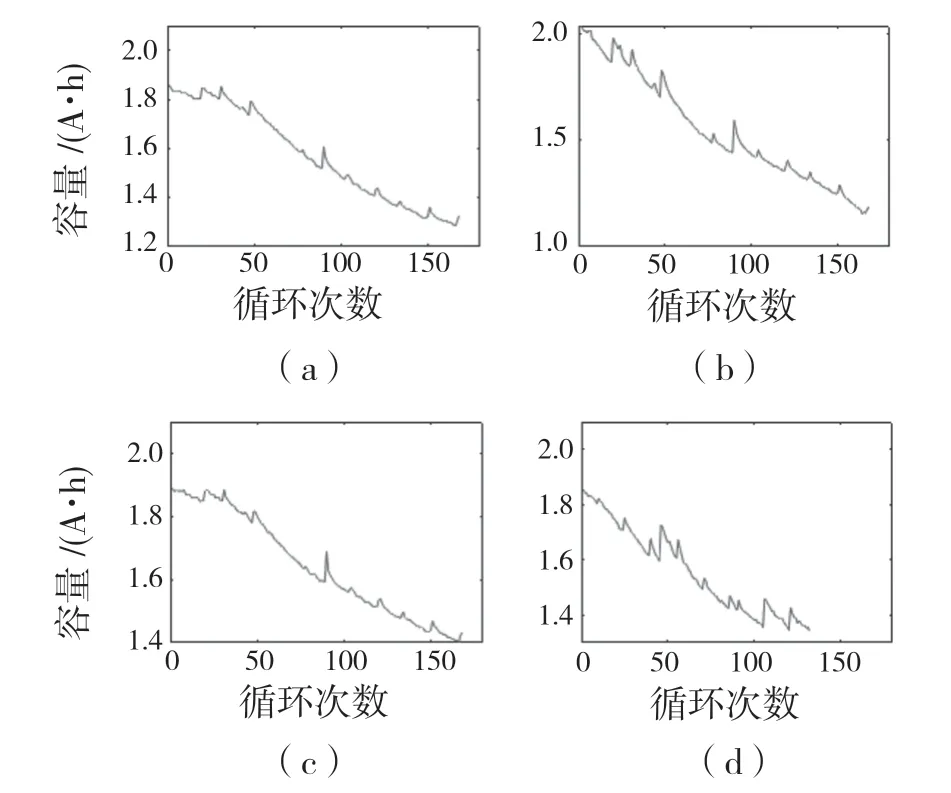
图2 4 个电池容量退化过程Fig.2 Capacity degradation process of four batteries

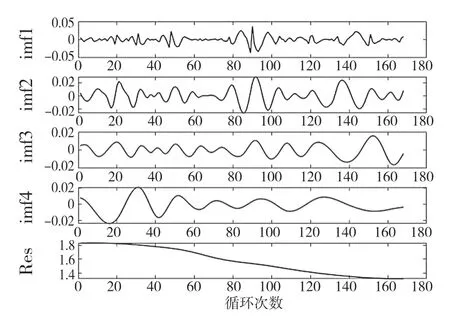
图3 B0005 锂离子电池容量EMD 分解效果图Fig.3 EMD decomposition effect of B0005 lithium ion battery capacity

3.1 锂离子电池剩余寿命的点预测

选取B0005 电池前125 次循环为训练组，第126-135 次循环为预测组进行验证。首先选取前125 组数据用于训练GPR 模型，接着对第126 组数据进行预测，并与实测值进行比较。获取容量预测值后，将125 组训练数据与新获取的1 组预测数据一起训练出新GPR 模型，预测第127 组数据，反复直至第135 次循环为止。

从图4 中可以观察出，点预测值的趋势与实测值走向相同，随着循环次数的增加误差增加。表1 列出了10 组GPR 点预测值与对比值之间的误差。对比误差值发现，点预测总体误差都比较小，单点误差绝对值最大为0.15%，随着循环次数的增加误差变得更大，误差变化速率更快。

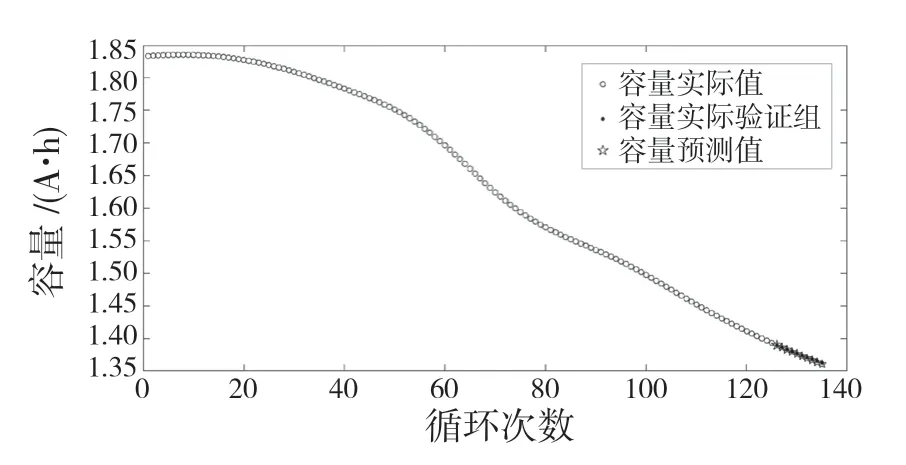
图4 B0005 电池容量的点预测结果Fig.4 Point prediction of battery capacity of B0005

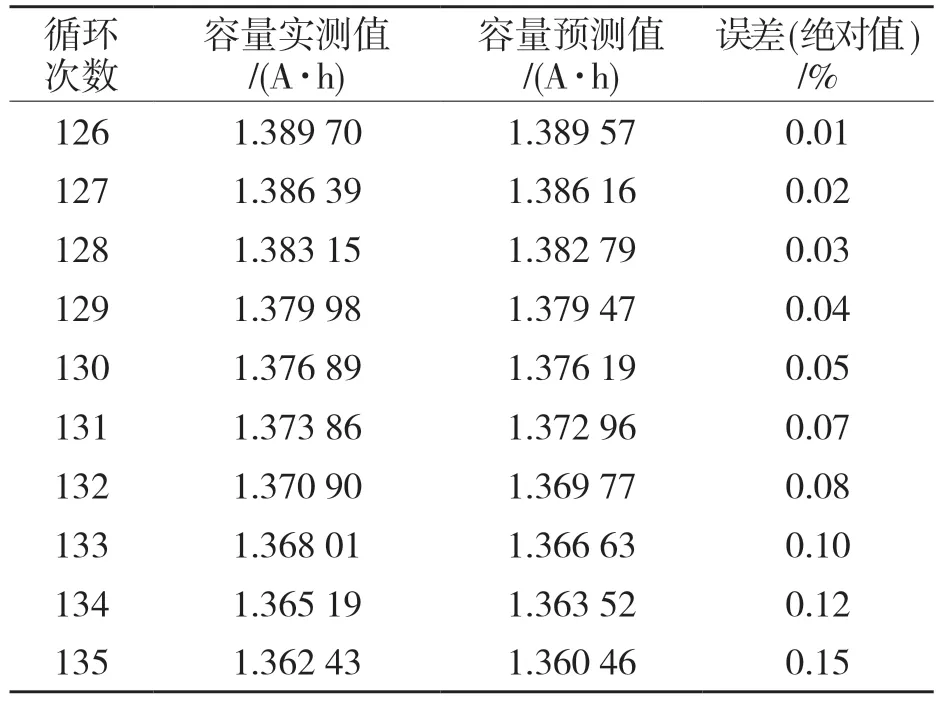
表1 容量预测误差对比Tab.1 Comparison of single-step capacity prediction errors

采用初始容量2 A·h 的75%作为失效阈值，即失效阈值为1.5 A·h，据此求得锂离子电池的剩余寿命。图5 为剩余寿命预测结果，图中黑色直线是设置的失效阈值，在黑色直线以下的点，设定为已经失效。由图5 可以观察出在失效阈值之下，实测容量值在第131 次循环时处于设定失效情况，即有效寿命为130 次。点预测值也在131 次失效，预测准确，因此可以判断出基于GPR 模型拟合的精度和预测的精度都比较高。

3.2 锂离子电池剩余寿命的区间预测

将B0005 电池容量作为GPR 模型的输入，预测均值以及均值上下限作为GPR 模型的输出，模型训练的预测效果如图6 所示。图中，GPR 预测的上下限之间的区域即95%电池容量预测置信区间。

图6 中，点线为容量75%失效阈值。可以观察到容量实测值的有效寿命为130 次，在容量置信区间的上下限之间的有效寿命预测为129～131 次，真实值就在预测的置信区间内。GPR 模型的区间预测结果不是单点的预测，而是以一个范围的预测结果呈现，所预测的寿命范围包括实测值的有效寿命，增加剩余寿命的预测结果的可靠性，能表现出变量的不确定性，提供更多的参考信息。

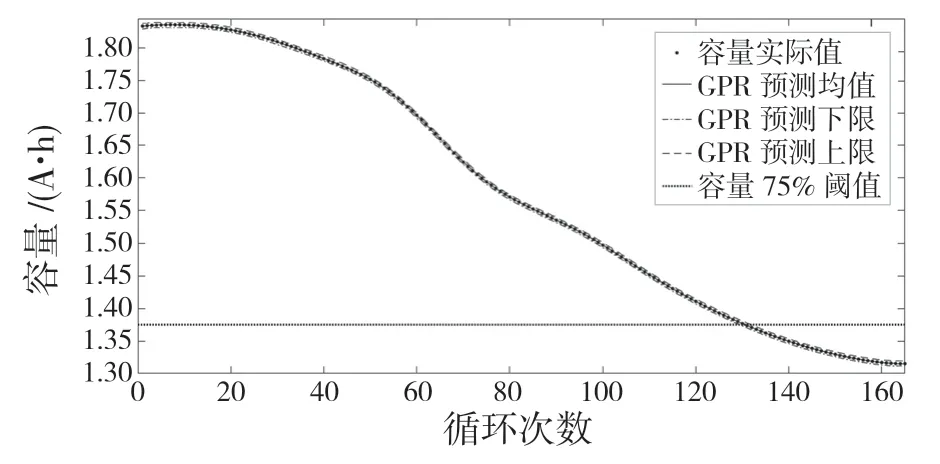
图6 电池剩余寿命的区间预测结果Fig.6 Interval prediction results of battery remaining life

4 结论

针对锂离子电池剩余寿命预测精度不高的问题，本文提出一种基于EMD 和GPR 的锂离子电池剩余寿命预测方法。通过研究分析得出以下结论：（1）利用EMD 将非线性的电池容量信号进行分解，获得趋势项，降低了数据的非平稳性和非线性，降低了容量退化过程中的波动量的干扰；（2）针对趋势项数据，选取马特恩函数构建GPR 预测模型，有效提高GPR 模型预测寿命的精度；（3）基于NASA 锂电池数据集进行验证，从点预测和区间预测两方面预测分析，点预测精度高，区间预测则可以表现出变量的不确定性，实验结果表明EMD-GPR 模型可以有效提高锂离子电池剩余寿命的预测精度。