弹性连杆式振动机工作过程的仿真分析

严跃拨，尹志宏，牛宪伟，勾富强

（1.650500 云南省 昆明市 昆明理工大学 机电工程学院；2.650500 云南省 昆明市 腾翎机械科技(云南)有限公司）

0 引言

振动筛作为一类散体物料筛分、选别和分级的设备，被广泛应用于建筑、矿业、石化、粮食等工业领域，其中弹性连杆式振动筛，因具有结构简单、工作可靠等特点，在工业领域得到广泛应用。为了提高振动筛的使用性能及工作效率，国内外学者做了广泛研究[1-5]。文献[6]利用动静法原理建立了单质体、双质体及多质体弹性连杆式振动筛的动力学模型，并给出其动力学参数计算公式；文献[7-10]是针对不同类型的振动筛利用多体动力学分析软件分析筛面的振幅变化情况以及频率、激振力、偏心质量等参数对振动系统的影响，主要针对稳态振动进行探讨。文献[11-13]是对振动筛的实验分析及相关参数的讨论，并研究了参数共振的问题。文献[14-15]对振动筛振动工作过程研究分析，利用数值解析法得出振动筛过渡过程的振幅变化曲线。

本文运用多体动力学ADAMS 仿真软件，研究弹性连杆式振动机空载工况下振动系统的幅值变化，分析振动机筛面的运动轨迹以及在电机起停阶段振动系统幅值的变化规律，为弹性连杆式振动机设计及优化提供理论依据。

1 振动筛的结构及工作原理

一种弹性连杆式振动机如图1 所示，筛面倾角为5°，由支撑底座、传动装置、工作机体及支板弹簧组成。传动装置包含电机、带轮、传动轴、偏心套、传动轴承、连杆臂以及拉杆，是振动机运行工作的动力来源。支板弹簧起支撑导向作用，使工作机体沿垂直于支板弹簧中心线方向做往复周期运动。

图1 弹性连杆式振动机Fig.1 Elastic link type vibration machine

电机输出动力通过带轮传递到传动轴，由传动轴上的偏心套通过传动轴承带动连杆臂运动，当物料倒入机架上的筛板后，连接连杆臂的拉杆带动机架做往复周期运动，物料受激振力的作用在筛面做斜抛运动，由于物料的饱满程度不同，其自身质量就不同，根据斜抛运动的远近程度，使得物料能够有效地进行选别和分级。

2 振动机运动学分析

根据对弹性连杆式振动机的工作过程及运动方式的分析，将其力学模型简化为单质体模型如图2 所示。参照力学模型，以水平为x 轴，竖直方向为y 轴，建立直角坐标系，应用力学中的动静法，得出振动机在x 方向上的振动微分方程，即

图2 力学模型Fig.2 Mechanical model

式（1）表明，系统刚度为支板弹簧与连杆弹簧刚度之和，该振动方程的解包含自由振动时的通解和强迫振动时的特解两部分。在振动机的运转工作过程中，由于阻尼力的影响，自由振动将会衰减至零，只发生强迫振动。解方程可得振动机在x 方向上的绝对位移

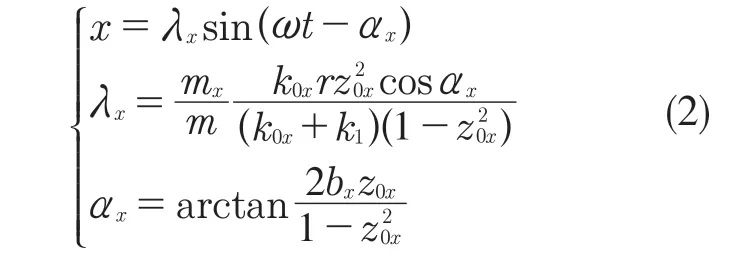
式中：λx——振动质体在x 方向上的振幅；mx——x 方向的诱导质量；αx——x 方向的位移落后于名义激振力的相位差角；z0x——x 方向的频率比，及工作频率ω比上固有频率ω0；bx——x 方向上的阻尼比。

同理可得，竖直方向上的绝对位移为

式中：λx——振动质体在y 方向的振幅；my——y 方向的诱导质量；αy——y 方向的位移落后于名义激振力的相位差角；z0y——y 方向的频率比；by——y 方向的阻尼比。

令δx=-αx，δy=90°-αy则振动机的绝对位移可表示为

式（4）表示相互垂直的x 方向和y 方向上同频率简谐振动，其合成的运动轨迹为椭圆方程

振动机的运动轨迹为椭圆，使其具有物料出筛分层效果好、筛分效率高等优点[16]。

3 振动机仿真模型的建立

在实际工程中，振动机的振动情况十分复杂，利用数值理论推导求解困难，因此选择多体动力学仿真分析软件ADAMS 对振动机振动系统进行设计、建模、仿真、分析。

3.1 三维模型的建立

根据对振动机的工作原理及运动情况分析，振动机工作机体在x，z 方向有明显的振幅变化，而在y 方向无明显振动变化，结合振动机在实际工作中的振动情况，将对实际工作中的弹性连杆式振动机模型进行以下简化处理：

（1）本文主要研究的是振动机工作机体质心处在整个工作过程中的振幅变化情况及运动轨迹分析，因此只针对主要零部件进行建模，而对于非主要零部件进行简化处理（如工作机体及底座等），但仍考虑简化后的结构对整体振动系统的影响。

（2）为降低仿真求解难度，减少约束添加，将对仿真过程没有影响的零件删除，对于不同零件做同一运动的部分进行布尔和运算，简化后的模型无冗余约束存在。

（3）仿真模型中相互运动的零部件间间隙忽略不计，弹簧质量忽略不计，其弹簧刚度、阻尼参数可调节。

（4）振动机在实际工作运行中，为使运行平缓，在偏心套与连杆臂间装配滚动轴承，起润滑缓冲作用，轴承工作时是通过各零件间相互接触传递运动，这时会形成复杂的接触问题，在仿真环境中通过轴承模块以运动副的形式来建立轴承模型，运动接触碰撞不影响整机系统振动。

（5）振动机的动力由三相异步电机提供，仿真模拟时根据实际实验的变化规律定义驱动函数，模拟出电机工作过程中转速的变化情况。

将简化后的模型导入ADAMS，对各零部件材料、参数、颜色等进行设置，如图3 所示。设置各零件间的约束、运动副等相关物理参数。其相对运动连接关系见表1。

图3 振动机仿真模型图Fig.3 Simulation model diagram of vibrating machine

表1 运动约束列表Tab.1 Motion constraints

3.2 仿真环境配置及参数设置

在ADAMS/View 模块中，选用笛卡尔坐标系描述振动系统的运动状态，采用Newton-Raphson迭代算法进行求解。根据实际情况，设置各零件材料属性、弹簧刚度、阻尼及重力加速度等初始参数，如表2 所示。根据表1 运动约束列表中约束关系创建运动副，共有5 个固定副，1 个转动副，1 个轴承副。此时，在ADAMS 中可计算得到振动固有频率为10.45 Hz，固有圆频率为65.66 rad/s，系统阻尼比为0.28。

表2 仿真参数汇总表Tab.2 Summary of simulation parameters

3.3 添加运动驱动

振动机所用的三相异步电机型号为Y90S-4，其详细相关参数见表3。根据电机的机械运动特性在仿真环境中设置驱动函数。在实际作业过程中，电动机转速从0 至1 400 r/min 到达额定转速需历时5 s，关闭电动机后，传动轴动力消失，振动机会因系统阻尼影响而逐渐停止运转，整个停车过程需10～20 s，因此设置0～5 s 时间段为电机的启动时间，5～20 s 时间段为平稳运转时间，20～35 s 时间段为电机停车时间。根据前文对模型的简化处理，驱动力直接添加到传动轴上，r1为小带轮半径，r2为大带轮半径，因此电机转动经带轮传动至传动轴的转速n 为

表3 Y90S-4 电机参数表Tab.3 Y90S-4 motor parameters

其旋转角速度为

故激振频率为

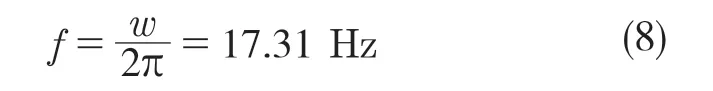
根据对振动机的工作运转情况分析，设置驱动函数为：step (time,0,0,5,6 232.26d)+step (time,20,0,35,-6 232.26d)，其中6 232.26°相当于1 038.71 r/min，其转速曲线图如图4 所示。

图4 驱动函数曲线图Fig.4 Drive function curve

4 仿真过程及结果分析

4.1 振动机运动轨迹分析

根据以上的仿真前处理后，设置仿真时间35 s，步长2 000 步进行仿真计算，其仿真结果经ADAMS 后处理模块导出，得到振动机空载作业下工作机体的运动轨迹如图5（a）所示；图5（b）表示0～5 s 时间段内振动机的运动轨迹，此时正好是电机的启动阶段，运动轨迹处于混沌状态；图5（c）为5～20 s 内的运动轨迹，电机转速到达额定转速，运行平稳，此时运动轨迹为椭圆形状；图5（d）为20～35 s 时间段内的运动轨迹，此时电机停止运转，属于振动机的停车阶段，运动轨迹混乱，且振动机逐渐停稳。振动机在启动阶段和停车阶段运动轨迹混乱，是由于在这两个阶段发生共振，激励突变引起的位移突变，过共振区后，以稳态振动工作，整个工作过程中的运动轨迹呈椭圆形状。

图5 质心运动轨迹图Fig.5 Centroid motion trajectory diagram

4.2 振动机启动阶段分析

设置仿真时间16 s，仿真步数为2 000 步，得到振动机上工作机体质心点处Z 方向上的振幅曲线如图6 所示，其速度变化与加速度变化曲线如图7、图8 所示，连接偏心套的连杆臂在质心点处的速度变化曲线图如图9 所示。仿真0～5 s时间段是电机的启动阶段，电机转速从0 升至额定转速1 400 r/min，此时振动机受外部激励影响发生振动，振动过程由稳态振动与瞬态振动叠加而成。由图6、图7 可知，振动系统在t=2.9 s 时，系统振幅达到最大值20.6 mm，此时传动轴转速达到644.87 r/min，激振频率为10.74 Hz，相应地质心点处速度达到最大，随着时间的增加，瞬态振动逐渐消失；在t=4.4 s 时，系统振动趋于稳态振动，稳态振动的振幅为8.3 mm，电转速达到额定转速，传动轴转速达到1 038.71 r/min，振动系统进入工作时域平稳运转。

图6 振动系统Z 方向上的位移Fig.6 Displacement in Z direction of the vibration system

图7 振动系统Z 方向上的速度Fig.7 Speed in the Z direction of vibration system

图8 振动系统Z 方向上的加速度Fig.8 Acceleration in Z direction of the vibration system

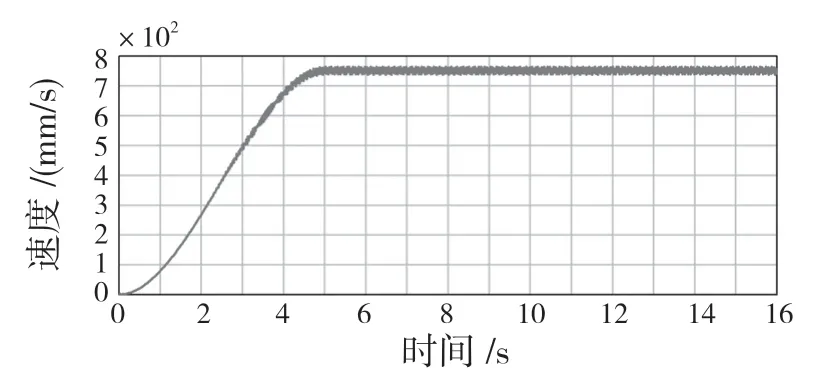
图9 连杆臂的速度变化曲线Fig.9 Speed change curve of the link arm

4.3 振动机停车阶段分析

关闭电机电源，外激振力消失，振动系统会因系统阻尼影响而逐渐停止振动，这一过程运用step 函数控制，设置仿真时间35 s，仿真步数为2 000 步。振动系统在Z 方向上的幅值变化如图10 所示，全程变化速度如图11。

图10 振动系统Z 方向上的位移Fig.10 Displacement in Z direction of the vibration system

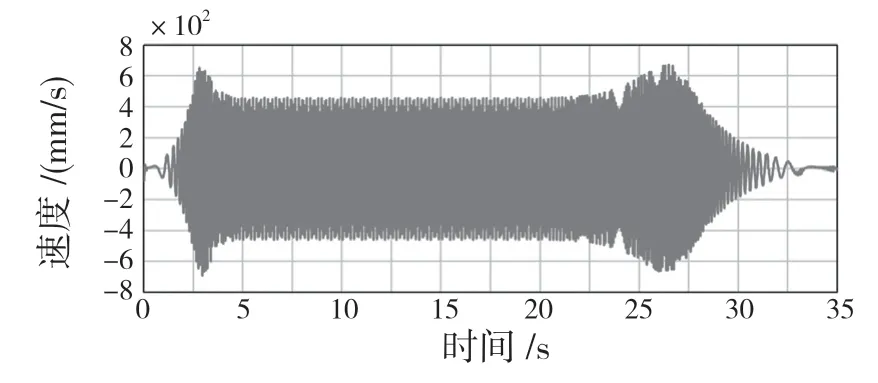
图11 振动系统Z 方向上的速度Fig.11 Speed in Z direction of the vibration system

由图10、图11 可以看出，在20～25 s 时间段内，振动速度加剧，振幅逐渐增大，最大振幅在t=26.7 s 时刻，其幅值为21 mm，传动轴转速为622.35 r/min，瞬时激振频率为10.37 Hz，振幅是系统稳态振动振幅的2.5 倍左右。

5 结论

建立弹性连杆式振动机动力学模型进行分析与仿真，得出弹性连杆式振动机的运动特性如下：

（1）仿真得到振动机筛面的运动轨迹呈椭圆形状，这与理论分析相符合。由于在启停阶段振动系统发生共振，筛面运动轨迹会出现短暂混乱，但整体运动形状仍是椭圆形状，这与实际观测到的振动情况相一致。

（2）过共振区时的变化规律：振动机在电机启动后，振动幅值逐渐增加，振动速度逐渐加快，当电机实际转速上升到额定转速的62%时，振动系统瞬态激振频率达到10.47 Hz，接近于固有频率10.45 Hz，振动幅值达到最大值；随着时间历程增加，系统激振频率逐渐远离固有频率，振动系统趋于稳态振动，此时设备进入工作状态，运行平稳；电机停止运转后，系统激振频率逐渐减小，减小至接近固有频率时，即传动轴转速下降到622.35 r/min 时，系统发生共振，振幅变大，此时振幅是系统稳态振动振幅的2.5 倍左右。