与弱倾斜模有关的对偶对
2021-11-26杨晓燕
罗 佩, 杨晓燕
(西北师范大学 数学与统计学院, 兰州 730070)
倾斜理论和对偶对理论在同调代数及相对同调代数中具有重要作用, 目前已取得了许多研究成果[1-4]. 文献[5]通过对弱倾斜模的研究将倾斜理论再次拓展, 得到了如下结果:R-模W是弱倾斜模当且仅当示性模W+=HomR(W,/)是余倾斜模. 文献[6]给出了对偶对的概念及相关例子. 文献[7-8]根据对偶对的性质(当(相关的模类及余挠对的性质.
1 预备知识

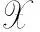
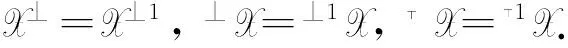
定义1[1]如果下列条件成立:
1)W的平坦维数有限;

3) 存在一个非负整数r和一个正合列0→Cr→Cr-1→…→C0→R+→0, 其中对于0≤i≤r有Ci∈Prod(W+).
则称R-模W是弱倾斜模. 若fdRW≤n, 则称W为弱n-倾斜模.
定义2[3]如果下列条件成立:
1)C的内射维数有限;
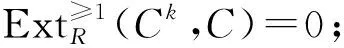
3) 存在一个非负整数r和一个正合列0→Cr→Cr-1→…→C0→U→0, 其中U是内射余生成子且对任意的0≤i≤r有Ci∈Prod(C).
则称R-模C是余倾斜模. 若idRC≤n, 则称C为n-余倾斜模.
定义3[2]如果下列条件成立:
2 主要结果
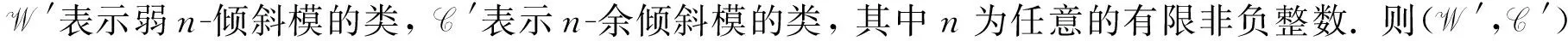

下面主要讨论与有限(n+1)-表示的弱n-倾斜模有关的对偶对以及与之相关模类的性质.




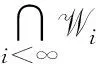
命题3令R是任意环, 则:

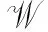


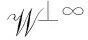

命题4令R是任意环, 则:
1)是投射可解类;
2) (,()是完全且遗传的余挠对.
证明: 1) 首先, 证()是对偶对. 对于任意的M, 有所以M∈关于有限直和及直和项封闭, 所以()是对偶对.
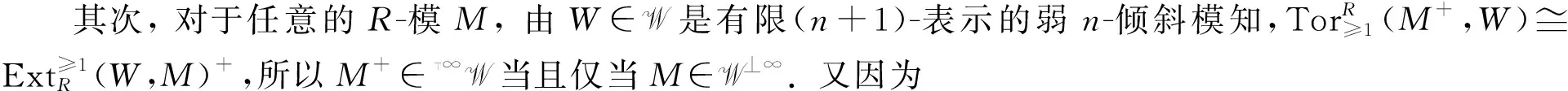
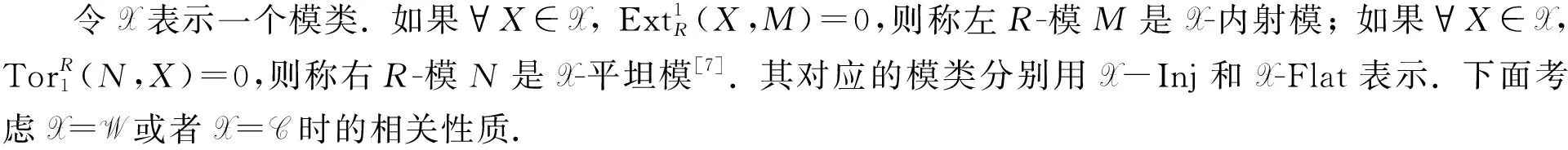
综上, 有:
定理1令R是任意环, 则:
命题5令R是任意环, 则:

证明: 1) 首先, 因为W是有限n-表示的模类, 所以有如下同构式:



…→Xn→…→X1→X0→M→0,
命题6令R是任意环, 则:
0→Xn→…→X1→X0→M→0,

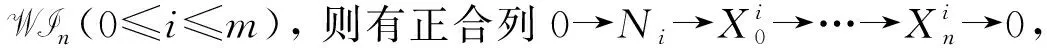


0→C+→B+→A+→0

综上, 有:
定理2令R是任意环, 则:
