海洋用液压转盘马达转速同步控制系统研究
2021-11-25时琦昊乔长奎魏孔财陈宁生宋志龙
时琦昊,乔长奎,魏孔财,陈宁生,宋志龙
(1.兰州兰石石油装备工程股份有限公司,兰州 730314;2.川庆钻探长庆钻井总公司,西安 710021;3.中国石油和石油化工设备工业协会,北京 100825)
目前,海洋用液压转盘主要在活动钻具、辅助MWD随钻测井中使用,或者为液压动力卡瓦在上卸扣时提供反转矩[1],具有低速大转矩及传动紧凑、安装尺寸小等特点。液压转盘的旋转主要是由布置在液压转盘4个角的4个液压马达驱动。
在活动钻具或者MWD随钻测井作业中,转盘复杂的外负载环境,导致液压马达转速波动,造成转速不同步,影响转盘控制精度,降低马达使用寿命。因此,应使液压转盘中的4个液压马达输出的转速同步。
根据液压控制原理,转盘中4个液压马达实现同步控制,主要是控制4个液压马达具有相同的进入流量。随着控制技术的不断发展,电液比例控制已经成为工程中主流的控制技术,在提高系统动态性及控制精度等方面效果明显[3-5]。因此,液压采用电液比例控制的方法,运用同等控制方式及控制算法[6-7]控制入4个液压马达的流量,提高马达转速同步的性能,使液压转盘能更好地适应现场工况的需求。
1 转盘同步控制系统设计
转盘同步控制原理如图1所示。为方便研究,将系统部件简化为液压泵站、比例阀、液压马达、转速传感器等。系统工作原理为:液压泵站为液压系统提供动力及限制最高工作压力;系统有4个液压马达,每个液压马达都有1个比例阀进行单独控制和对应的转速传感器采集其转速信息,采集到的转速信号传送到控制器中,由控制器对其进行计算,计算后的信号被送入比例放大器中,信号经比例放大后,进入比例阀中,形成1个闭环的马达转速同步控制系统。
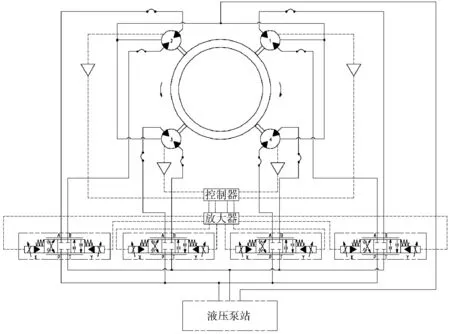
图1 转盘同步控制系统原理
系统技术参数如表1。

表1 转盘控制系统技术参数
为方便对系统进行研究,选用DPZA/-A-L5/24型比例阀和190-0236型液压马达。
2 马达电液比例控制数学模型
马达电液比例控制原理如图2所示。

图2 马达电液比例控制原理
2.1 比例放大器
比例放大器高的频率响应对系统影响较小,可将输出比例放大器的电流I和输入电压U近似为比例关系[8],用增益Ka来表示传递函数:
(1)
2.2 电液比例阀控马达方程
2.2.1 比例阀流量方程
比例阀线性后增量方程:
ΔQL=KXΔX-KPΔpL
(2)
式中:KX为流量增益;KP为流量压力系数;ΔpL为马达进回油压力差;ΔX阀芯位移差;ΔQL为阀流量的增量。
2.2.2 马达流量连续方程
为方便建模和研究单马达控制特性,做如下假设[9-10]:
1) 连接阀与液压马达的管道对称且短而粗,管道压力损失和动态忽略不计。
2) 油液温度和体积弹性模量恒定。
3) 液压马达内泄漏均为层流流动。
4) 供油压力恒定且回油无背压。
根据以上假设,马达流量连续方程为:
(3)
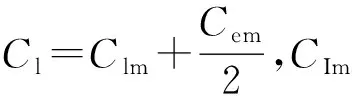
2.2.3 液压马达扭矩方程
马达转矩负载平衡方程为:
(4)
式中:T为马达输出转矩,N·m;J为液压马达轴上的总惯量,kg·m2;Bm为马达、负载粘性阻尼系数;G为弹性联轴器刚度,(N·m)/rad;TL为马达轴上干扰负载转矩,N·m。
2.3 各系统传递函数
对式(2)进行拉氏变换:
QL(s)=KXX(s)-KPpL(s)
(5)
对式(3)进行拉氏变换:
(6)
对式(4)进行拉氏变换:
T=Bmsθc(s)+Js2θc(s)+Gθc(s)+TL
(7)
整理式(5)~(7)并简化,忽略阀控马达弹簧负载。当G=0,可得液压马达输出的转角:
(8)
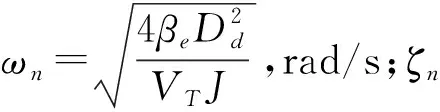
马达转角对阀芯位移的传递函数:
(9)
马达转角对外负载的传递函数:
(10)
2.4 转速传感器传递函数
将马达转速信号转换为电压信号输出:
(11)
式中:Us为转速传感器输出电压,V;Km为转速传感器增益。
对式(11)进行拉氏变换:
Gθ(s)=Kms
(12)
2.5 马达比例控制系统传递函数
根据以上公式,可得系统开环传递函数:
(13)
参照文献[10]中参数处理的办法,结合本系统,得出表2数学模型参数。
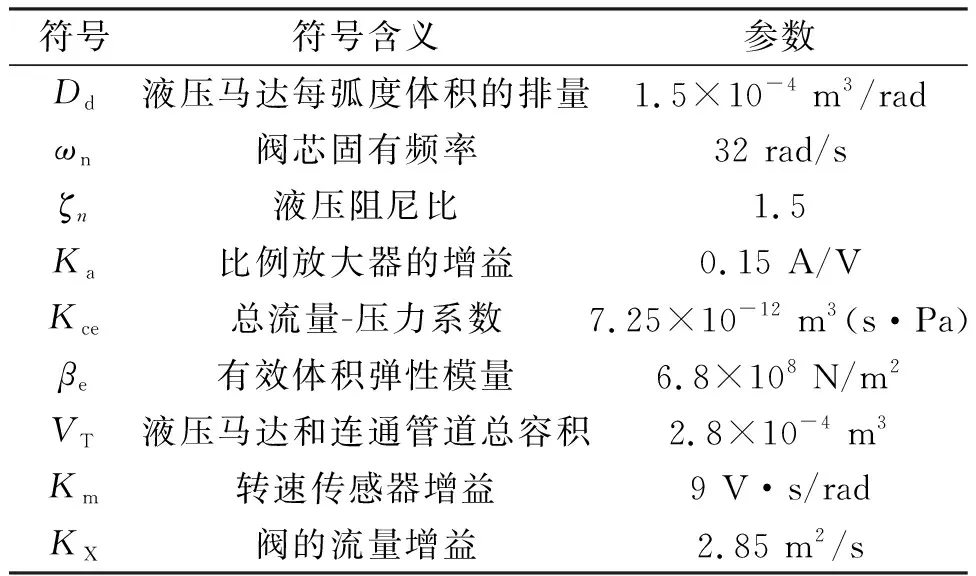
表2 数学模型参数
将表1和表2中的参数代进式(13),得到系统的开环传递函数为:
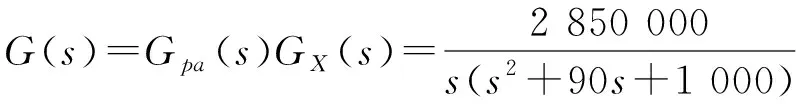
(14)
根据式(14),采用时域分析的方法,求解控制系统闭环特征方程的根的方法来判断系统的稳定性,即,如果求解的根实部大于零,则判断系统不稳定,非线性。反之,则系统稳定[11]。利用Matlab对式(14)求解其闭环特征方程的根,求解程序如下[12]:
num=2850000;den=[1 90 1000 0];
s=tf(num,den);
sys=feedback(s,1);
roots(sys.den{1})
程序运行后可得:
ans =
-1.7616 + 0.0000i
0.4308 + 1.1968i
0.4308 - 1.1968i
根据计算结果,可知马达同步控制系统为非线性系统。因此,需要加入相应的控制算法,以提高系统的同步控制精度。
3 自整定模糊PID控制器设计
3.1 控制原理
控制原理如图3所示。系统反馈误差E和误差变化EC为输入,匹配模糊规则,整定出调节PID参数的调整量,即ΔKp、ΔKi、ΔKd。在系统运行中,呈现动态变化,不断检测,并适时修正,以达到控制预设的目标值。此控制器适应系统内部参数变化,克服外界干扰的能力强,使被控对象具有良好的动态和静态特性[13]。
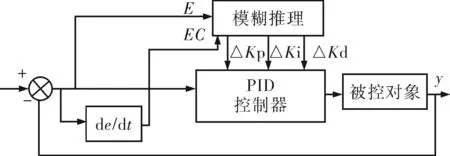
图3 控制器工作原理
3.2 控制器设计
运用Matlab/Simulink软件对自整定模糊PID控制器进行设计。
3.2.1 各变量隶属度函数的确定
如图3所示,定义E和EC、ΔKp、ΔKi、ΔKd的模糊子集及含义为{NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)};定义论域的范围在[-6,6];在模糊逻辑工具箱的隶属度函数编辑器中,将输入量E和EC的隶属函数选为高斯型,输出ΔKp、ΔKi、ΔKd的隶属函数为三角形[14-15]。
3.2.2 参数隶属度函数曲线设计
模糊控制编辑器如图4所示。
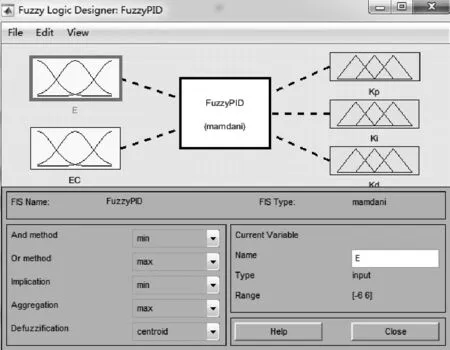
图4 模糊控制编辑器
E和EC的隶属函数曲线如图5所示。
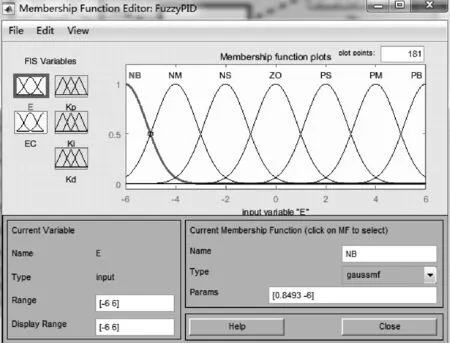
图5 E和EC的隶属度函数曲线
ΔKp、ΔKi和ΔKd隶属度函数曲线如图6所示。
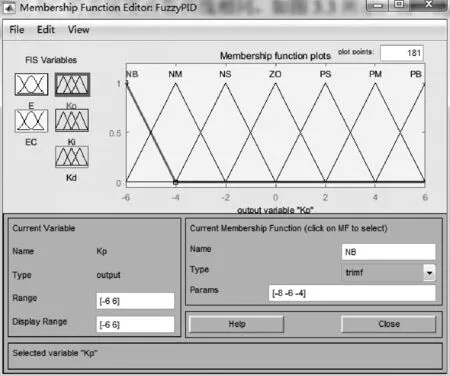
图6 ΔKp、ΔKi和ΔKd隶属度函数曲线
3.2.3 模糊推理规则设计
在Malab/Simulink中编辑适合本系统需求的模糊推理规则,如图7所示。
至此,完成自整定模糊PID控制器设计。
4 系统仿真
根据本系统数学模型,利用Matlab/Simulink
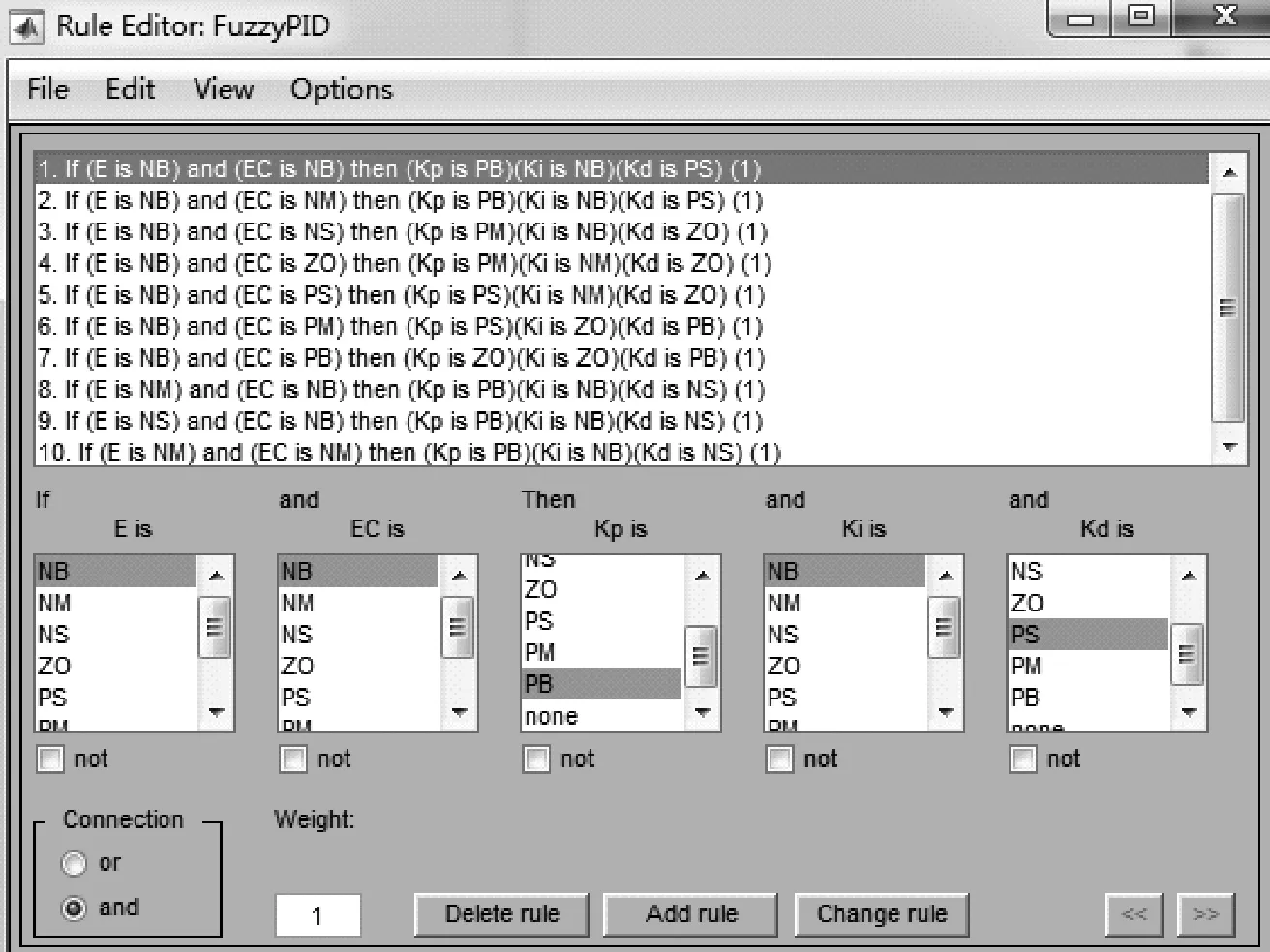
图7 模糊推理规则设计
建立其控制系统。采用PID控制及参数自整定模糊PID控制两种控制算法分别对马达同步系统进行控制,并对2种控制算法的仿真结果进行分析,以验证其有效性。
由于液压转盘在实际应用中,所受负载因钻井工况的影响,会不断的变化,因此,负载的变化假定按正弦曲线规律变化。
4.1 PID控制系统模型
根据式(9)和式(10),得出单液压马达控制系统simulink模型,如图8所示。
依据图8,得出4个马达控制系统simulink模型,如图9所示。

图9 PID四液压马达控制系统Smulink模型
4.2 自整定模糊PID控制系统模型
根据式(10)和式(11),得出单马达控制系统simulink模型,如图10所示。其中,PID控制器和模糊控制器的simulink模型如图11~12所示。
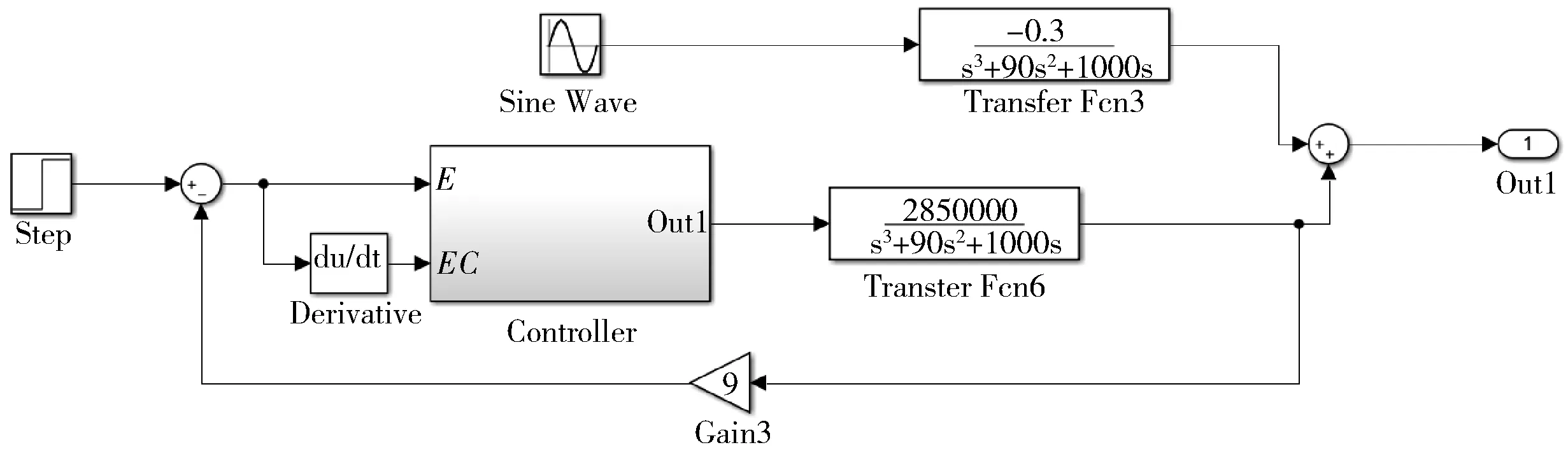
图10 单马达自整定模糊PID控制Simulink模型
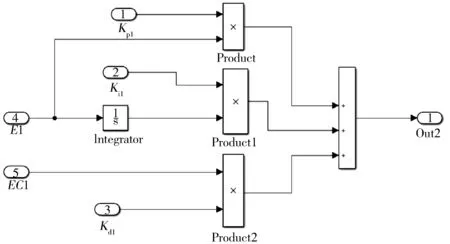
图11 PID控制器模型
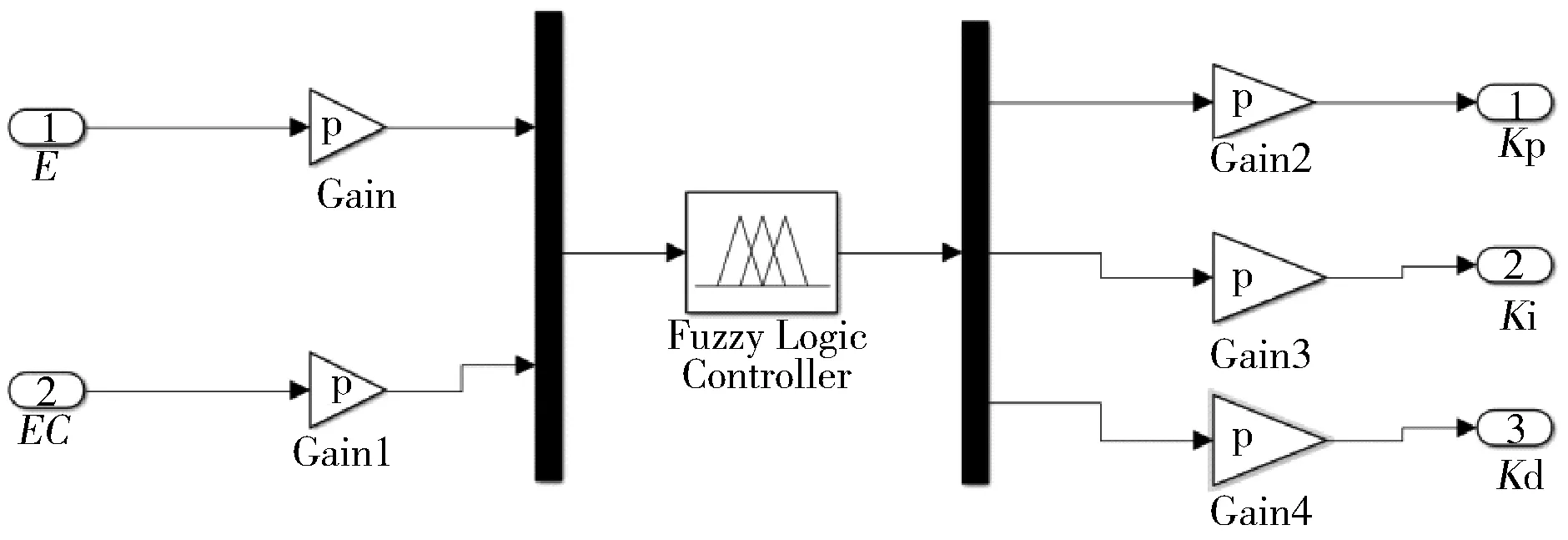
图12 模糊控制器模型
依据图10~12,得出本系统同步马达控制simulink模型,如图13所示。

图13 四马达自整定模糊PID控制Smulink模型
4.3 Simulation仿真
按以下步骤进行仿真:
1) 设定系统仿真采样时间为1 s。
2) 试凑PID的3个参数,最终得出Kp=0.25、Ki=0.24、Kd=0.02。
3) 根据步骤2),将3个参数代入控制器中。
4) 液压转盘在最大转矩下的转速约为6 r/min,因此设置理想转速为此转速。
根据以上步骤,分别采用PID控制器和自整定模糊PID控制器对液压转盘马达同步控制系统进行仿真分析。
4.3.1 PID控制仿真
4个马达的转速在PID控制器调节下,得出以下控制结果:
1) 在复杂工况变负载的环境下,系统稳定后,最大转速偏差为0.28 r/min,同步性较好,如图14所示。
2) 最大同步偏差为0.55 r/min,如图15所示。
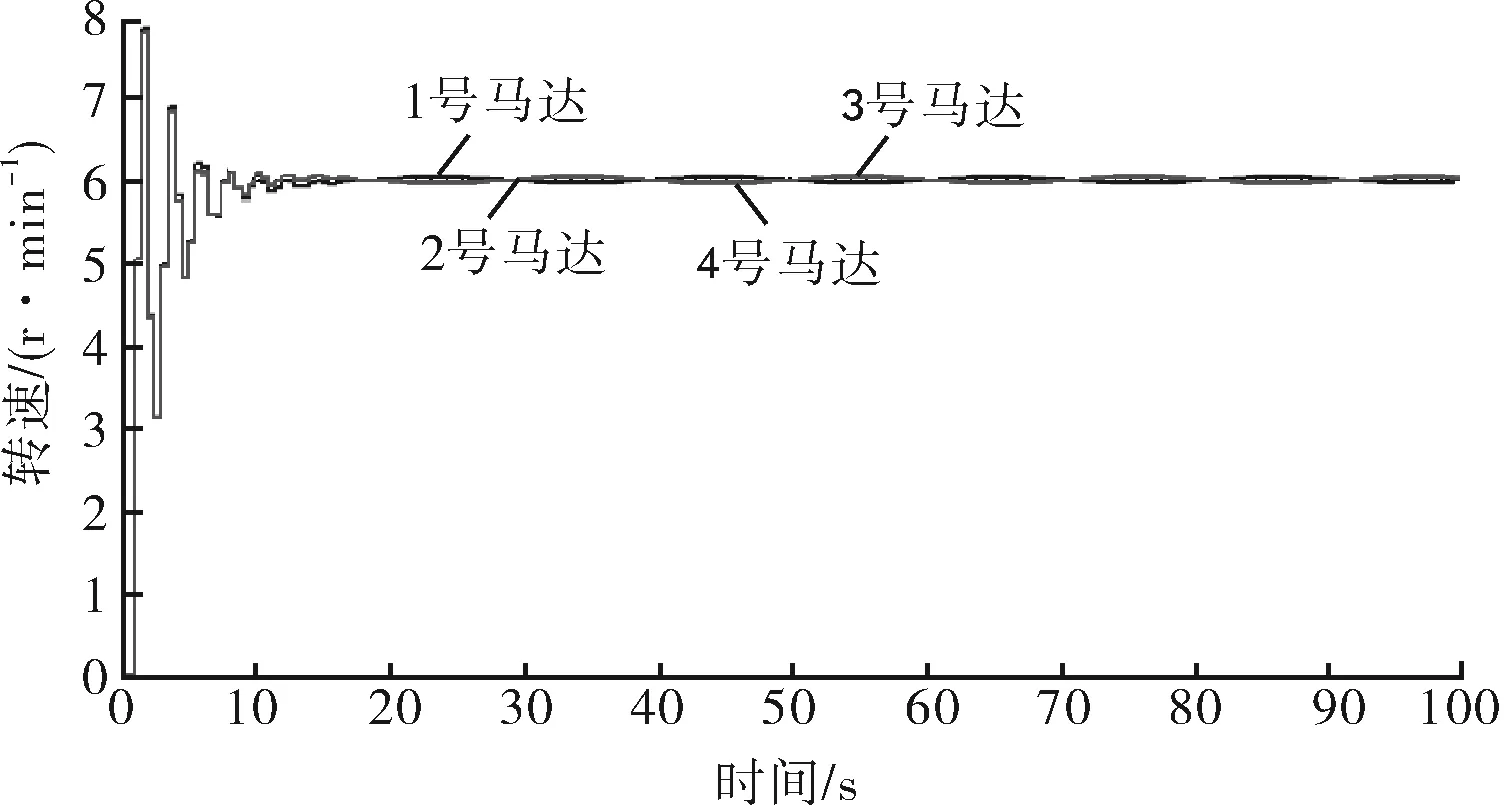
图14 4个马达在PID控制下转速曲线
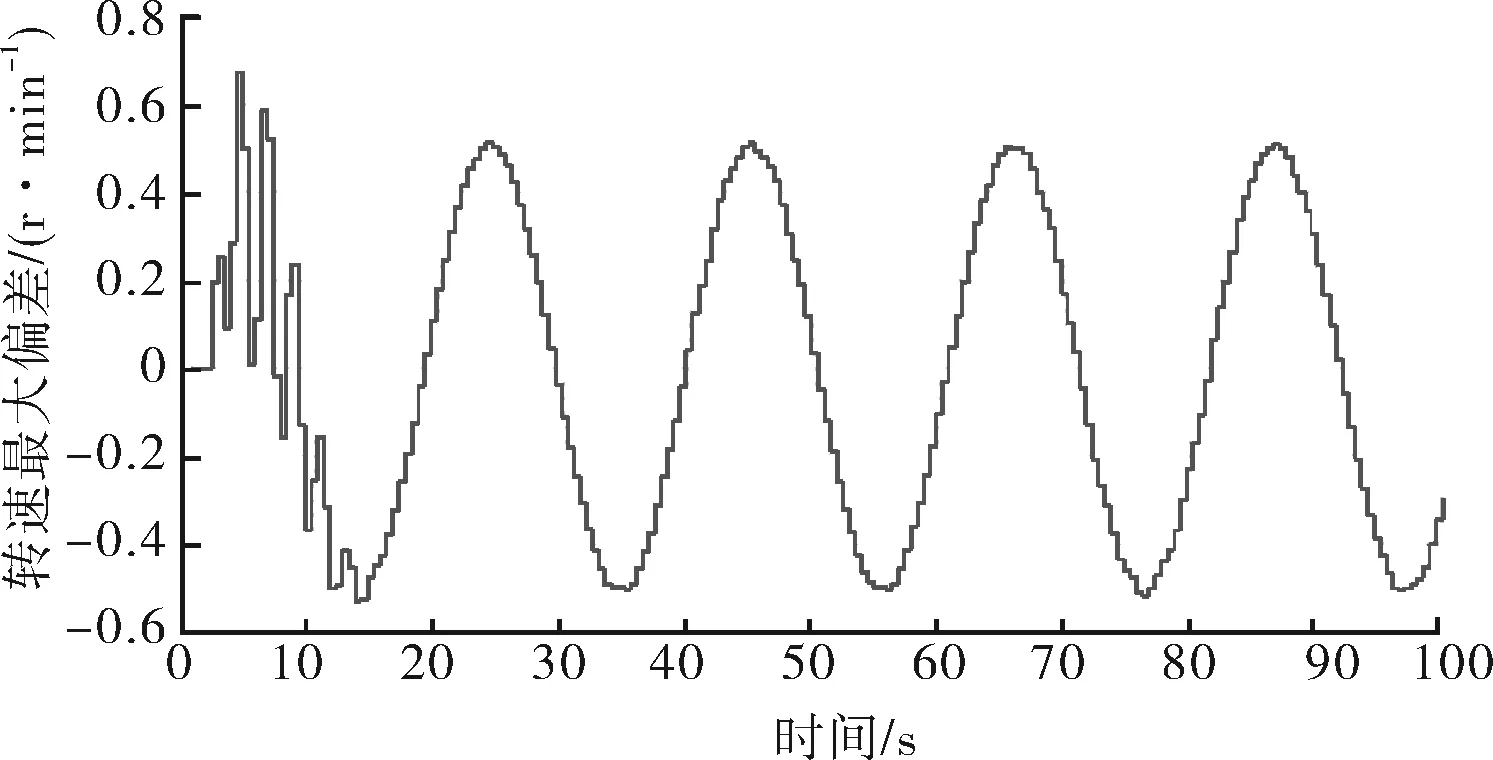
图15 4个马达在PID控制下转速最大偏差曲线
4.3.2 自整定模糊PID控制仿真
4个马达的转速在自整定模糊PID控制器调节下,得出以下控制结果:
1) 在复杂工况变负载的环境下,系统稳定后,最大转速偏差为0.28 r/min,如图16所示。
2) 最大同步偏差为0.37 r/min,如图17所示。
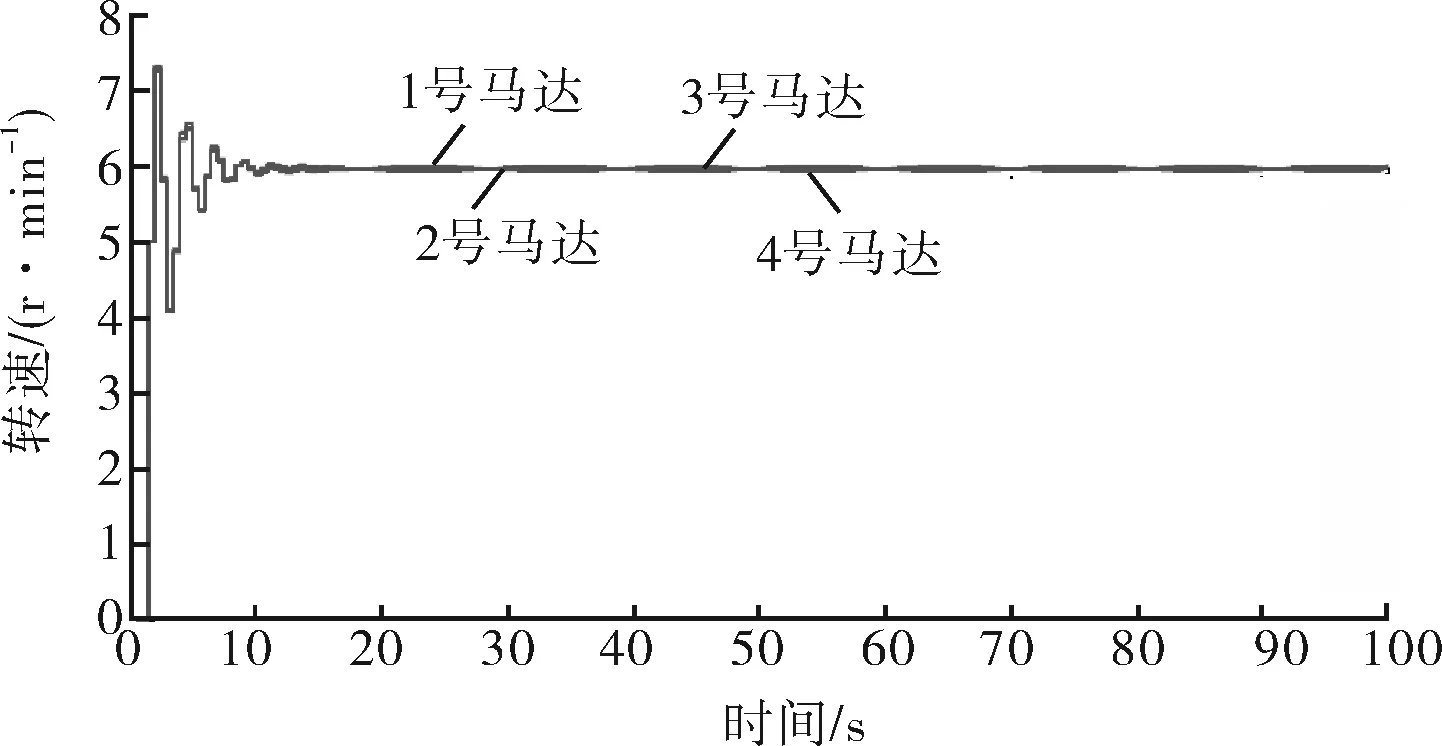
图16 4个马达在自整定模糊PID控制下的转速曲线
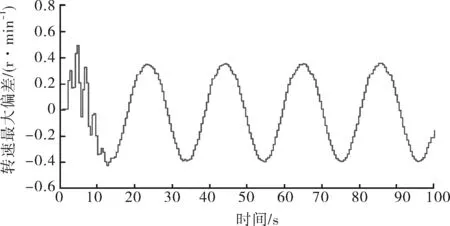
图17 4个马达在自整定模糊PID控制下转速的最大偏差曲线
5 结语
1) 针对液压转盘马达转速存在不同步的问题,通过设计同步控制系统,分析系统数学模型,研究其动态特性,采用增加控制算法的方式,使4个液压马达输出转速同步效果得到改善,系统稳定性增强,具有较强的环境变负载适应能力,同时也延长液压马达的使用寿命。
2) 通过对液压转盘同步控制系统仿真验证可知,自整定模糊PID的控制效果好于单纯PID控制,更适用于控制性能要求较高的工程领域。
3) 经对液压转盘同步控制系统的研究,其控制思路亦可用于石油钻采设备及井口自动化机具,且具有多液压马达同时工作并需要同步的情形,对此类同步控制系统具有参考意义。
