爆炸载荷下双层梯度夹芯板的抗爆性能
2021-11-25赵相江马小敏李世强徐礼佳吴桂英
赵相江,马小敏,李世强,徐礼佳,吴桂英
(1.太原理工大学 机械与运载工程学院 应用力学研究所,太原 030024;2.南京粒子声学科技有限公司,南京 210000)
夹芯结构具有质量轻、强度高、刚度大、缓冲吸能效果良好等诸多优势,被广泛应用于建筑行业、汽车工业、航空航天等领域。
近几十年来,不同学者对夹芯结构的抗爆性能进行了多方面的研究。KARAGIOZOVA et al[1]通过实验和数值模拟分析,发现蜂窝多孔材料作为抗爆结构的芯层可以提高整体结构的抗爆性能。ZHU et al[2-3]通过对蜂窝夹芯结构进行大量实验和仿真模拟,初步发现采用相对密度较大的芯层可以减小后面板的挠度。LI et al[4]通过实验和仿真分析了不同结构的夹芯结构在爆炸载荷下的响应过程,发现芯层在能量吸收过程中占主导地位。张旭红等[5]采用弹道冲击摆系统研究了爆炸载荷作用下的铝蜂窝夹芯结构的动力响应,并将后面板的变形作为衡量夹芯结构抗爆性能的主要参数。LI et al[6-7]通过实验和LS-DYNA软件对梯度铝蜂窝夹芯结构在爆炸载荷作用下的结构响应和抗爆性能进行了分析,结果表明相对密度较大的芯层靠近冲击面板放置具有更好的抗冲击性能。杨森等[8]利用非线性动力学软件AUTODYN对铝蜂窝夹芯结构在爆炸冲击载荷作用下的失稳过程进行数值模拟研究,发现增加芯层的壁厚以及高度可以增强夹芯结构抵抗变形的能力。PYDAH et al[9]研究了Miura-ori和蜂窝芯组合而成的双层芯夹板结构在爆炸载荷下塑性耗散能的大小,发现上芯层结构的形状尺寸参数对塑性耗散能的影响很大。目前,有关蜂窝夹芯结构的抗爆性能的研究表明芯层是主要的吸能部件,在梯度夹芯结构中采用相对密度较大的芯层作为上芯层具备更好的抗爆性能,芯层尺寸参数对夹芯结构抗爆性能的影响有待进一步研究。
本文在课题组现有研究基础上,发现三层梯度夹芯结构的抗爆性能受芯层尺寸参数的影响较大[10],三层夹芯结构在爆炸载荷下的芯层参数研究较为复杂。为了进一步深入研究芯层尺寸参数对夹芯结构抗爆性能的影响,本文制备了和文献[10]相同材料的芯层相对密度从大到小的纤维增强双层蜂窝夹芯结构,利用弹道冲击摆锤系统对夹芯结构进行不同质量炸药下的爆炸实验研究,并运用Abaqus/Explicit对三层和两层夹芯板实验结果行数值模拟验证。进一步保持下芯层不改变,改变上芯层孔边长和壁厚来得到上芯层相对密度一致和相对密度逐渐增大的夹芯结构,分析芯层尺寸参数对夹芯结构抗爆性能的影响,为夹芯结构进一步的优化提供基础。
1 实验
1.1 实验试件
实验中双层夹芯结构以玄武岩纤维增强铝合金层合板为面板、铝合金正六边形蜂窝芯为芯层,试件的组成示意图如图1(a)所示。试件的各部分之间通过环氧树脂粘结剂(Eploam5015/5015)进行粘结,并用水刀切割为300 mm×300 mm的方形板。面板铝合金层的材料型号为AA-6061,玄武岩纤维层型号为FGM-W-0002,铝蜂窝芯材料型号为AA-5052.单个蜂窝芯层高度为10 mm,蜂窝芯孔壁厚为0.04 mm,蜂窝芯孔孔边长为2 mm和2.5 mm两种类型。在芯层之间加入厚度为0.1 mm铝合金界面板,可以防止芯层间的相互侵入。
本文以HC-2(0.04)-2.5(0.04)来定义夹芯结构的类型,其中HC代表蜂窝芯层(honeycomb core),2(0.04)代表上芯层蜂窝孔边长2 mm、壁厚0.04 mm,2.5(0.04)代表下芯层蜂窝孔边长2.5 mm、壁厚0.04 mm.蜂窝芯层的初始相对密度可以通过公式(1)计算得到[7]:
(1)
式中:τ为蜂窝芯孔的壁厚,a为蜂窝芯孔边长,θ为蜂窝芯孔扩张角,ρ0为蜂窝芯层的材料密度,六边形蜂窝孔的几何尺寸如图1(b)所示。

图1 试件及蜂窝尺寸示意图Fig.1 The diagram of specimen and honeycomb core size
1.2 实验装置
实验装置采用四钢索弹道冲击摆锤测量系统,如图2所示。冲击摆锤部分由夹具、工字梁以及配重组成,工字梁通过4条钢索(长2.6 m)悬挂于钢梁上,试件通过16根φ16 mm螺栓固定在夹具中,试件有效载荷面积为250 mm×250 mm.炸药为球状的乳化炸药(当量约为TNT的0.7倍)[11],放置于距离前面板中心点d处。炸药起爆后作用于试件,使得整个摆锤系统作近似单摆运动(摆动角度<2°),通过位于摆锤系统后方的激光位移传感器记录摆锤摆动的位移时间曲线,进一步可以确定试件受到的冲量。实验分别对双层梯度夹芯结构HC-2(0.04)-2.5(0.04)在相同的起爆距离d=50 mm和不同的炸药质量m=10,15,20 g三种条件下进行爆炸载荷研究,实验结果相对的结构受到的冲量大小分别为9.33、18.82、25.43 N·s,结构受到的冲量通过实验记录的位移进行计算[12]:
(2)
式中:M为冲击摆锤的总质量(m=151.3 kg),T为摆的摆动周期(T=3.14 s),x1、x2分别为T/4、3T/4时摆锤位移大小。

图2 实验装置Fig.2 Experimental setup
1.3 实验结果分析
实验中不同爆炸载荷下双层梯度蜂窝夹芯结构的变形失效模态如图3所示。在夹芯结构受到的冲量较小时(I=9.33 N·s),如图3(a)-(c)所示,前面板上除雷管碎片冲击产生的小孔外并未发生破坏,前后面板与芯层仅仅发生微小的整体塑性变形。随着夹芯结构受到的冲量增大(I=18.82 N·s),如图3(d)-(f)所示,前面板的中心区域出现了小范围撕裂破坏并伴有压入变形,芯层出现圆形区域局部压缩屈曲,后面板的整体塑性变形增大但未发生破坏。当夹芯结构受到的冲量继续增大(I=25.43 N·s),如图3(g)-(i)所示,前面板的中心撕裂破坏区域增大并有明显的压入变形,芯层中心圆形压缩区域增大并发生贯穿失效,进一步使得后面板受到的冲击较大,而后面板的整体塑性变形继续增加,同时中心区域出现不规则的凸起变形,这主要是因为后面板铝合金层和纤维层之间的界面粘结强度较低,在较大冲量下芯层中心区域完全破坏压缩,导致后面板受到较大冲击,后面板的铝层和纤维层出现脱胶分层,进一步纤维层回弹使得铝层发生面内挤压变形。实验发现,前面板破坏越大,芯层压缩也越完全,进一步会影响后面板的变形失效形式。
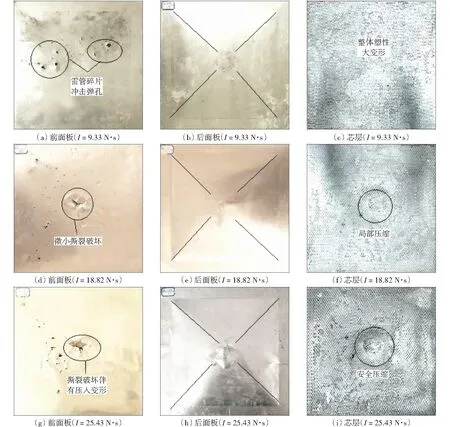
图3 夹芯结构变形失效模态Fig.3 Deformation Modes of the sandwich
2 数值模拟
2.1 有限元模型
根据载荷和结构的对称性,选取整个双层夹芯结构的1/2在Abaqus/Explicit中建立有限元分析模型。对整个夹芯结构的中心横截面Y-Z面上施加对称约束,夹具进行定义刚体(Rigid body)并施加固定约束(约束所有自由度);夹具和试件之间采用通用接触(GENERAL_CONTACT),设置硬接触;面板中铝合金层和纤维层之间采用粘性接触(COHESIVE_SURFACE);面板和芯层之间以及芯层和界面板之间采用绑定(Tie)约束,面板、界面板、夹具部分的网格类型采用C3D8R实体单元,蜂窝芯层采用S4R壳单元。对面板的中心区域进行网格细化,芯层的网格采用统一的大小,有限元模型和网格划分情况如图4所示。

图4 有限元模型示意图Fig.4 Schematic of numerical model
结构受到的爆炸载荷随时间和空间的分布如下[10]:
(3)
(4)
式中:t0=0.013 ms,t1=0.014 ms,R0=6 mm,Rb=150 mm,k为压力空间分布衰减指数,k=55 m-1.
2.2 材料属性参数
基于三维单向复合材料Hashin准则,建立平纹复合材料的三维渐进损伤模型,并运用VUMAT子程序对正交编织玄武岩纤维布损伤过程进行模拟[10]。不同材料的力学属性参数如表1所示,玄武岩纤维的材料参数和文献[10]一致。
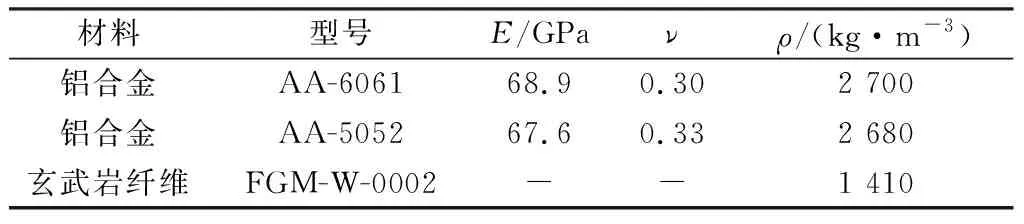
表1 材料力学属性参数Table 1 Mechanical property
强动载荷下金属材料的力学行为运用Johnson-Cook模型(J-C模型)可以很好地体现,铝合金材料的J-C模型参数如表2所示。忽略温度的影响,J-C模型本构关系为:
σγ=(A+Bεn)(1+Clnε*) .
(5)
式中:A为材料初始屈服强度,B为材料应变强化模量,n为材料应变强化指数,C为经验性应变率敏感参数,ε*=ε/ε0为无量纲应变率,ε0为参考应变率。

表2 J-C塑性模型参数[13-15]Table 2 Parameters of J-C plasticity model[13-15]
2.3 数值模拟验证
针对文献[10]有关三层梯度夹芯结构的实验研究,选取A组和B组的三层蜂窝夹芯结构以及本文实验中两层蜂窝夹芯结构进行数值模拟验证。结果显示,不同药量下的实验与模拟中后面板的中心点残余挠度对比如图5(a)所示,发现实验和数值模拟结果基本分布在斜率为1的直线附近。实验和数值模拟的夹芯结构前后面板及芯层的变形模态如图5(b)所示,发现前面板的裂纹形状基本相似,裂纹长宽数值基本一致;后面板均未发生破坏,呈现整体塑性大变形;芯层区域出现类似的圆形压缩区域,压缩面积基本一致,数值模拟的结果略大于实验结果,这是由于数值模拟过程中使用Tie约束代替粘性接触使得前面板的压入变形持续作用于芯层,忽略了实际中的面板弹性回弹效应,对于此类塑性大变形问题,弹性效应影响较小。
夹芯结构在不同冲量下后面板的中心截面实验和数值模拟残余挠度曲线对比如图5(c)所示,实验和数值模拟变形失效模式和后面板残余挠度曲线基本一致。综上所述,本文有限元模型能够较好地模拟爆炸载荷下梯度夹芯结构的动力学行为。
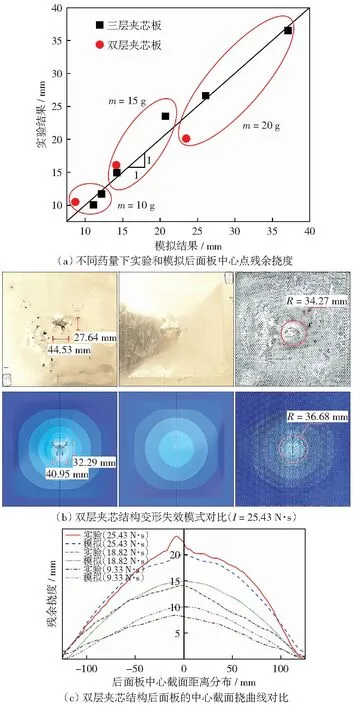
图5 实验和数值模拟结果对比Fig.5 Comparison of experimental and simulated results
2.4 数值模拟结果分析
夹芯结构作为吸能防护结构,后面板的变形是衡量夹芯结构抗爆性能的重要指标。本节通过数值模拟得到夹芯结构后面板中心点的残余挠度,以此来衡量双层夹芯结构的抗爆性能。
为了消除夹芯结构质量不同的影响,需要对数值模拟中的后面板中心点残余挠度和结构受到的冲量进行无量纲处理,得到无量纲冲量、无量纲残余挠度[16]:
(6)
(7)
式中:I0为夹芯结构单位面积受到的冲量,m0为夹芯结构单位面积质量;σfy为面板材料的流动应力,ρf为面板材料的密度,二者采用公式混合法进行计算[17],如公式(8)所示;δmax为后面板的残余挠度。
(8)
式中:σAl、σcomp分别为纤维材料的极限抗拉强度和铝合金的抗拉强度,hAl、hcomp分别为铝层和纤维层的总厚度。
在实验试件的基础上,保持夹芯结构下芯层的孔边长和壁厚不变(孔边长2.5 mm,孔壁厚0.04 mm),建立3组上芯层孔边长和壁厚同比增加的双层梯度夹芯结构试件,3组试件的上芯层孔边长和壁厚如表3所示,分别对3组夹芯结构进行不同冲量下的数值模拟。
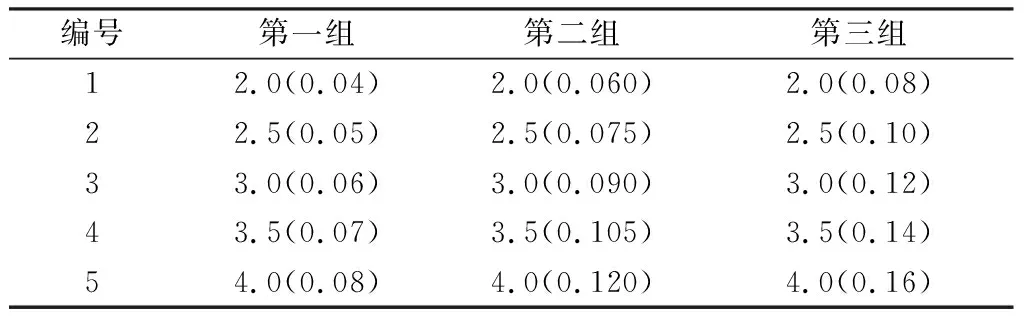
表3 三组试件上芯层尺寸大小Table 3 Size of upper core layer of three groups of specimens mm
三组试件在不同冲量下后面板中心点残余挠度如图6所示。可以看出,冲量较小(I=9.33 N·s、18.82 N·s)时,三组夹芯结构的后面板残余挠度差值较小,其中上下芯层孔边长一致的夹芯结构(第一、二、三组2号试件)后面板的残余挠度相对其他试件更小。冲量较大(I=25.43 N·s)时,第一、二组试件随着孔边长和壁厚的同比增加,后面板的残余挠度先减小后增大;上芯层孔边长为4 mm且壁厚大于0.08 mm的夹芯结构(第二、三组5号试件)后面板都出现了贯穿破坏;同时第二、三组2号和3号试件残余挠度明显增加,并且出现了变形失效模式的变化,整体塑性大变形转变为中心区域前面板、上芯层的破坏及下芯层的压缩屈曲,这主要是边长越长,芯层支撑面跨度越大,壁厚越厚支撑处刚度越大,面外载荷作用下前面板出现剪切失效,进一步导致结构变形局部化,因此后面板的中心区域挠度增加较明显。综上所述,上下芯层孔边长一致的夹芯结构在不同冲量下均可以有良好的抗爆性能。

图6 不同冲量下三组试件的后面板残余挠度Fig.6 Residual deflection of back panel of three groups of specimens under different impulse
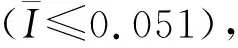
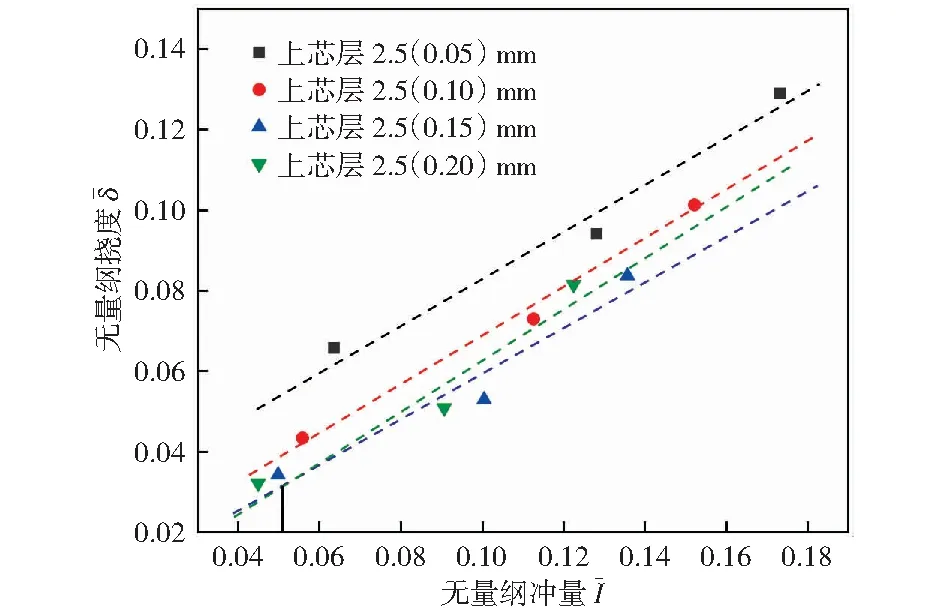
图7 无量纲冲量和无量纲挠度关系Fig.7 Normalized impulse and normalized deflection
3 结论
本文主要通过实验和数值模拟手段分析了不同冲量下芯层几何尺寸对梯度夹芯结构抗爆性能的影响,在本文研究范围内得到以下结论:
1) 爆炸载荷作用下双层梯度夹芯结构的变形失效模式与载荷强度及芯层配置密切相关,主要表现为:a.整体的塑性大变形;b.中心区域前面板的破坏及芯层压缩屈曲;c.中心区域前面板及芯层的贯穿失效;
2) 数值模拟表明,在夹芯结构整体质量相同的情况下,上下芯层边长一致的试件具有较好的抗爆性能;
3) 保持上下芯层边长一致的情况下,双层梯度夹芯结构的抗爆性能与上下芯层的相对密度的比值密切相关,上下芯层相对密度比值在3∶1左右时,结构具有更优的抗爆性能。
