挤压性围岩大变形危险性评价的组合赋权-理想点模型

2021-11-25周航陈仕阔刘彤李涵睿

中南大学学报（自然科学版） 2021年10期

周航，陈仕阔，刘彤，李涵睿

（西南交通大学地球科学与环境工程学院，四川成都，611756）

随着我国铁（公）路网建设重心逐步西移，西部山区隧道多向深埋长大趋势发展，围岩大变形地质灾害的发生频率也越来越高。严重的大变形会引起边墙开裂甚至造成支护结构挤压性变形破坏，严重影响隧道工程的施工安全、工期以及工程造价，如成兰铁路杨家坪隧道[1]、川藏公路鹧鸪山隧道[2]、兰新铁路乌鞘岭隧道[3]、南昆铁路竹箐隧道[4]等都受到不同程度的影响。开展围岩大变形灾害评估研究并合理地进行危险性等级划分，是深埋长大隧道建设中亟待解决的关键难题。

地下工程围岩大变形的理论研究始于RABCEWICZ[5]提出新奥法（NATM）原理。随后，国内外众多学者对围岩大变形的孕育机理、影响因素及变形机制等开展了广泛研究。例如，陈宗基[6]通过研究发现，隧道掘进过程，围岩应力释放破坏了其三向平衡状态，围岩发生变形和破坏之前积累了大量的应变能，且围岩的卸荷回弹变形能力与地应力呈正相关。BROX 等[7]重点关注受断裂带影响的工程案例，认为隧道开挖后断裂带处的应力重分布是引起围岩大变形的主控因素之一。ANAGNOSTOU 等[[8-9]均认为挤压性大变形的发生主要取决于岩石强度和地应力。李春林等[10]以龙溪隧道为例，研究发现构造应力和岩体结构是影响围岩大变形的主要原因。鄢建华[11]研究围岩大变形发生的基本特征及主控因素，揭示了围岩大变形的形成及发展过程，系统地探讨了大变形的影响因素和孕育机理。郑朋强等[12]在大量岩石试验的基础上，通过数值模拟计算分析了高地应力软岩巷道的变形机制。上述研究成果找到了影响围岩大变形的主要因素，对研究不同工程地质条件下隧道围岩大变形的发生规律并进行评价预测提供了重要的理论参考。

目前常用的围岩大变形判据有围岩强度应力比[13]、岩体质量分级[14]、隧道围岩相对变形量[15]等方法。需要特别指出的是，相对变形量是累进性变形和时间效应的直观体现，但是在隧道选线设计阶段其适用性较差，取而代之可以用统计分析和模拟方法来进行初步预测研判。陈卫忠等[16]构建了一种基于修正BQ值的软岩隧道挤压变形预测模型，分析了国内外多条隧道变形量监测的统计结果，验证了其模型的可靠性。王开洋等[17]结合围岩强度应力比法和三维数值模拟分析，对我国西南某隧道开挖过程中的大变形等级和位置进行了预测评价。此外，HOEK等[18]建立了一种表征岩体强度的地质指标评价体系，并对挤压因子进行了修正，在结合隧道围岩相对变形量的基础上，根据围岩的挤压程度将大变形分为5个等级。上述探索大变形预测评价的方法虽然都不同程度地抓住了围岩大变形机理研究中的某一本质特征，但预测结果仍然受一些因素影响而存在偏差，实用性受到一定限制，除受复杂地质条件影响外，这主要是上述预测方法和判据大多只考虑1～2个主控因素的影响或服务于隧道建设的不同阶段，很难全面反映复杂条件下围岩大变形产生的作用机理。

随后，许多学者开始尝试结合多因素指标并引入相应的数学评价模型来进行综合预测，并对一些地下工程的围岩大变形问题进行了评价。FENG 等[19]采用二分类Logistic 回归对大变形发生的概率进行了预测。国威[20]采用灰色理论和神经网络的方法，建立了隧道大变形风险评价模型，在白马隧道围岩大变形位移评估中得到了较好的验证。范建海等[21]建立了一种基于层次分析-模糊综合评判的软岩隧道大变形评估模型，并划分了大变形风险等级。李天斌等[22]提出并构建了大变形综合集成方法体系，在结合工程地质分析以及隧道施工超前地质预报的基础上，对隧道围岩大变形进行了综合预测和评价。上述研究极大地拓宽了围岩大变形研究的广度，取得了相应的研究成果，但由于大变形的发生机理和形成机制复杂，影响因素众多，仍存在以下问题需要进一步深化完善：1）评价指标的选取过多依赖于主观经验，个别缺乏必要的理论支撑；2）评价指标权重的确定依赖于专家经验和主观赋值，实际应用时在一定程度上取决于从业人员的专业知识，对其要求较高；3）除评价结果受主观因素影响较大外，个别方法存在不确定因素多、计算冗余等问题。

理想点法是一种能集中反映多种影响因素并进行综合评价的定量分析方法[23]。目前，该方法在线站选址[24]、油气管道运输[25]、隧道岩爆[26]等领域得到了一定的应用，但是根据现有文献，尚未发现用于隧道围岩大变形预测的相关成果。基于此，本文将大变形预测问题作为分类问题处理，引入理想点法对挤压性围岩大变形进行综合评价，其关键在于如何确定各评价指标并赋予合理的权重。目前，确定指标权重的主观分析方法主要包括层次分析法、优序图法、三角模糊法等，客观分析方法主要有熵权法、粗糙集法、标准离差法等[27]。大量工程实践表明，上述方法单独使用时，往往导致指标权重的差异性较大，由此得到的权重系数与真实情况不符。因此，本文结合层次分析法和熵权法，通过引入距离函数判别法，建立组合赋权规则来对围岩大变形的评价指标赋予权重，以消除指标的差异性，同时使得权重的确定更加科学、全面。为此，本文作者构建一种基于组合赋权-理想点法的挤压性围岩大变形预测模型，并将其应用于典型的隧道案例，进行围岩大变形预测评价，以验证该模型的可行性和准确性。

1 挤压性围岩大变形机理及影响因素

1.1 挤压性围岩大变形机理及分类

围岩大变形机理研究方面，TERZAGHI[28]提出并定义了挤压性和膨胀性岩石的概念。挤压性岩石中的云母矿物成分质量分数较高或黏土矿物成分质量分数较低，岩石侵入隧道开挖掌子面附近时没有明显的体积增加；而膨胀性岩石是指岩石矿物成分中含有蒙脱石、高岭石、伊利石等膨胀性矿物，侵入隧道开挖掌子面附近时有明显的体积增加。学者们一般将隧道围岩大变形分为挤压性和膨胀性2类。膨胀性大变形通常发生在膨胀性岩石中，而非膨胀性岩石中的大变形往往是由岩体受挤压作用造成的。目前，大部分学者都认为挤压作用在围岩大变形中占有更重要的位置，是围岩大变形的主要作用机制[22]。

高地应力环境和软弱围岩是发生挤压性围岩大变形的2个必要条件[8-9,29]。变形量大、持续时间长且破坏性强是挤压性大变形最典型的特征。现有挤压性围岩大变形隧道的地应力测试结果表明，隧址区中的最大水平主应力和自重应力至少有一种处于较高水平。此外，隧道开挖揭示掌子面，附近围岩常有扭曲、褶皱等现象，间接证明了高地应力环境存在强烈的挤压作用。根据应力场类型将挤压性围岩大变形分为自重型、构造型和复合型[30]，如表1所示。

表1 挤压性围岩大变形分类（据文献[30]修改）Table 1 Squeezed large deformation classification（modified from Ref.[30]）

1.2 挤压性围岩大变形影响因素

挤压性围岩大变形的发生受地层岩性、围岩性质、最大主应力、地质构造等多种地质因素的影响。本文通过研究成兰铁路杨家坪、茂县隧道，成昆铁路某隧道，兰新铁路大梁、乌鞘岭隧道，兰渝铁路毛羽山、两水隧道，川藏铁路某隧道，云桂铁路对门山隧道，丽香铁路中义隧道，都汶公路龙溪隧道等典型大变形隧道案例[1,3,10,22,29-39]，整理65 个大变形区段与大变形等级相关的数据资料，发现围岩洞壁最大主应力σmax、岩石抗压强度σc、围岩强度应力比σb/σmax、岩石弹性模量E、围岩级别K、地质构造S、地下水W这些共性特征对隧道大变形影响相对明显，并参考前人相关研究成果[7-12]，以客观反映高地应力环境、围岩性质和岩性条件3个方面因素为基本前提，重点对该7项指标进行详细的统计分析和研究。在此基础上，参照TB10003—2016“铁路隧道设计规范”[40]，根据围岩强度应力比和围岩变形特征将大变形等级分为轻微大变形（Ⅰ级，相对变形量为3%～5%）、中等大变形（Ⅱ级，相对变形量为5%～8%）和强烈大变形（Ⅲ级，相对变形量大于8%）。

1.2.1 地应力

高地应力是隧道工程围岩发生变形和破坏的关键性因素。根据大变形等级与最大主应力的关系（图1）可知：产生大变形的区段其主应力普遍较高，平均主应力达到22.3 MPa。69.3%的大变形发生在应力超过20 MPa 的围岩中，30.7%发生在应力低于20 MPa 的围岩中。虽然大变形等级随最大主应力的变化分布较离散，但随着最大主应力增加，大变形等级逐渐向高值区间靠拢，且低值区间的隧道大变形等级也有所降低。

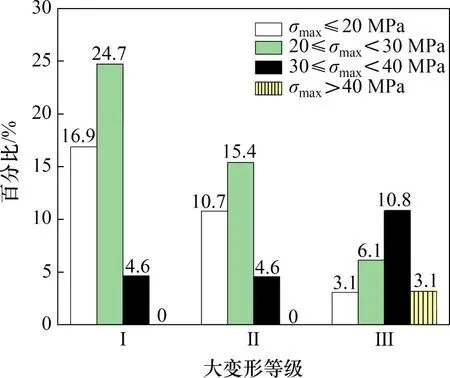
图1 大变形等级与最大主应力σmax的关系Fig.1 Relationship between large deformation grade and maximum principal stress

1.2.2 岩石强度

工程实践表明，挤压性大变形通常发生在千枚岩、片岩、板岩、页岩、泥岩等典型软弱围岩中，强度低、黏土质量分数高是软弱围岩的典型特征。图2所示为大变形等级与岩石抗压强度σc的关系。由图2可知：61.5%的大变形区段的岩石抗压强度处于1～15 MPa，平均岩石抗压强度为13.1 MPa，部分较硬岩如石英砂岩、闪长岩的抗压强度超过了30 MPa。虽然隧道大变形等级没有随岩石抗压强度提高而线性降低，但岩石强度高值区间发生的大变形等级较低且数量急剧减少。

图2 大变形等级与岩石抗压强度σc的关系Fig.2 Relationship between large deformation grade and compressive strength of rock

1.2.3 围岩强度应力比

围岩强度应力比法是TB10003—2016“铁路隧道设计规范”[40]有关高地应力区隧道软岩大变形分级方法，也是目前铁路隧道前期线路勘察设计和后期施工建设中最常用的大变形判别法。通过分析大变形等级和围岩强度应力比的关系（图3），强烈大变形主要分布在0～0.15区间，而轻微大变形和中等大变形的规律性不够明显。虽然隧道大变形等级没有随围岩强度应力比增大而出现显著降低，但围岩强度应力比高值区间的大变形等级较低且数量极少。

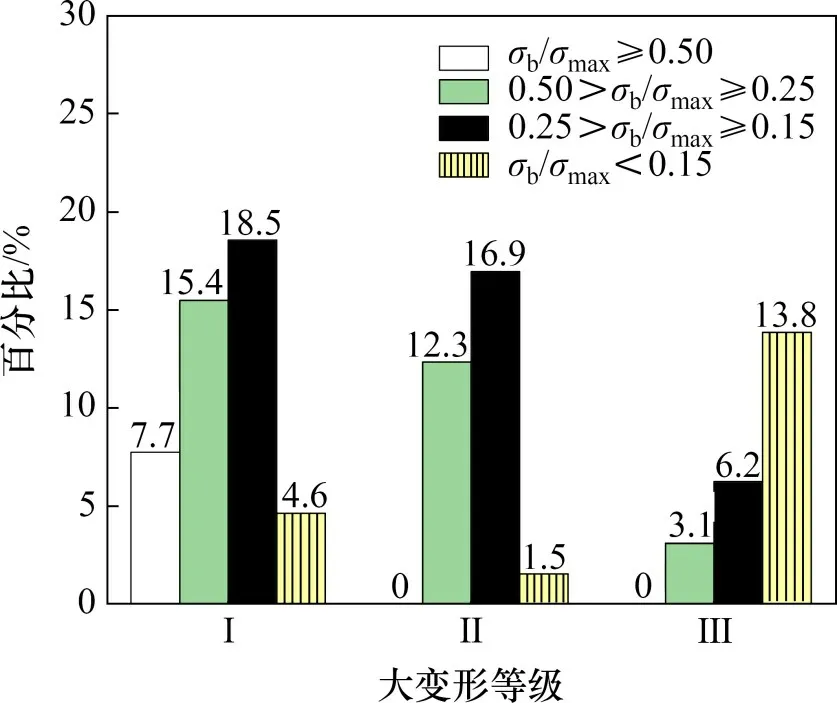
图3 大变形等级与围岩强度应力比σb/σmax的关系Fig.3 Relationship between large deformation grade and strength stress ratio of surrounding rock

1.2.4 岩石弹性模量

岩石弹性模量越低，发生挤压性大变形的可能性和等级越高[22]。本文统计的65 个大变形区段其发生频率与岩石弹性模量的关系，如图4所示。从图4可知：84.6%的大变形发生在岩石弹性模量小于2.0 GPa 的地层中，只有15.4%发生在岩石弹性模量大于2.0 GPa的地层中。

图4 大变形等级与岩石弹性模量E的关系Fig.4 Relationship between large deformation grade and elastic modulus of rock

1.2.5 围岩级别

隧道开挖改变了围岩的三向平衡状态，引起围岩应力重新分布，局部出现应力集中现象。围岩级别客观地反映了围岩的稳定性，也可以作为大变形的重要表征。图5所示为大变形区段的发生频率与围岩级别的关系。从图5可知：93.9%的大变形发生于Ⅳ级和Ⅴ级围岩中，仅6.1%发生在Ⅰ～Ⅲ级围岩中。根据现有研究以及大量隧道工程案例可知，在岩体结构和围岩性质较差的高地应力环境中，大变形风险可能比较突出，围岩与支护结构的挤压性变形破坏特征明显。

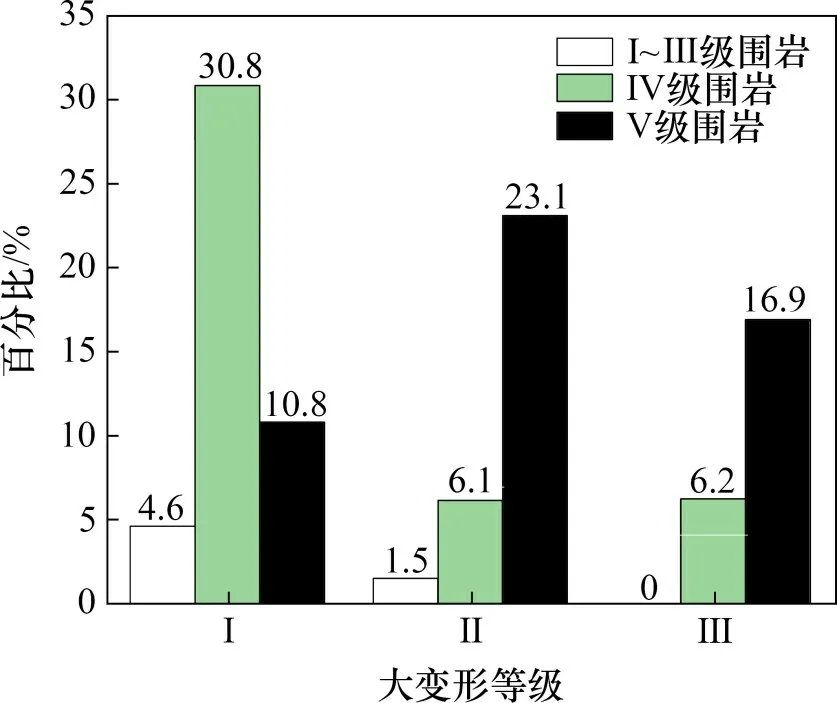
图5 大变形等级与围岩级别K的关系Fig.5 Relationship between large deformation grade and surrounding rock level

1.2.6 地质构造

地质构造对大变形的影响主要表现在地应力、围岩级别和岩石性质几方面，这种交互影响是一种综合性的体现。根据大变形等级与地质构造的关系（图6）可知：69.2%的大变形发生在褶皱核部、断层破碎带及断层处。究其原因，地壳运动形成挤压带、褶皱和断层的过程中，产生了大量的弹性应变能，造成围岩破碎使岩体完整性变差，特别是受软弱围岩变形性质影响，这种条件下进行隧道开挖，发生大变形的可能性和危害性均较大。

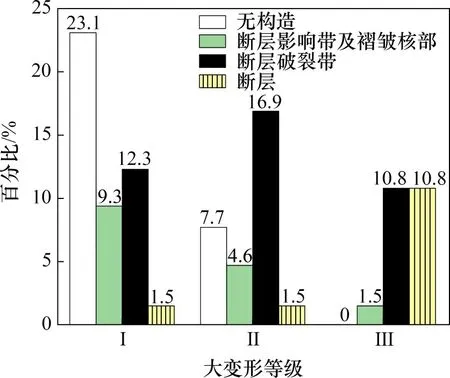
图6 大变形等级与地质构造S的关系Fig.6 Relationship between large deformation grade and geological structure

1.2.7 地下水状况

地下水是影响大变形发生与否的重要条件之一。含水量高的岩石，一般节理裂隙较发育，水岩作用会对岩石强度和变形性质等产生影响，进而加剧围岩变形。图7所示为大变形等级与地下水情况的关系。从图7可知：73.9%发生大变形的区域都存在地下水，26.1%发生大变形的区域位于干燥环境。

图7 大变形等级与地下水W的关系Fig.7 Relationship between large deformation grade and groundwater

综上所述，挤压性围岩大变形主要受控于外部和内部必要条件。高地应力环境是产生挤压性大变形的外部必要条件之一，围岩洞壁最大主应力越高，可能发生大变形的等级和风险越高；围岩强度应力比综合考虑了岩体抗压强度和围岩洞壁最大主应力的影响，更能反映大变形的形成原因；地质构造显著影响地应力的大小和方向，也是体现高地应力环境的重要指标，当然其量化指标在应用时仍需进一步细化。此外，隧道埋深虽然在一定程度上能够反映地应力，但它是一个经验指标[41]，与大变形的发生没有直接关系，因此不再考虑隧道埋深指标。围岩级别是反映围岩性质的一个综合性指标，地下水会与岩体发生水-岩相互作用，对围岩性质产生影响。岩性条件也是产生挤压性大变形的内部必要条件之一，岩石抗压强度和岩石弹性模量越低，发生挤压性大变形的可能性和等级越高。需要指出的是，岩石冻融及冻胀是高寒高海拔地区隧道特有的风险因素[42]，而这些深埋隧道的埋深大多都在600～1 600 m 范围，其影响程度需要进行专门评估，本文暂未涉及这些风险因素影响。因此，后续的分析评价所选用的最终指标仍以上述7项为依据来进行计算。

由于理想点法将各评价指标以函数形式进行处理和计算，需将围岩级别、地质构造和地下水特征的定性描述转化为可量化指标。在结合刘志春等[3,22,31]提出的隧道围岩大变形分级标准的基础上，并参考TB 10003—2016“铁路隧道设计规范”[40]，综合确定大变形等级与各评价指标的关系。围岩级别特征按照Ⅰ～Ⅲ级（＜4）、Ⅳ级（4～5）、Ⅴ级（5～6）、Ⅵ级（＞6）划分；地质构造特征按照无构造（＜4）、断层影响带及褶皱核部（4～5）、断层破碎带（5～6）、断层（＞6）划分；地下水特征按照干燥（＜2）、干燥～渗水（2～3）、渗水～滴水（3～6）、滴水～线状流水（＞6）划分。同时，将大变形等级划分为4个级别，即无大变形、轻微大变形（Ⅰ级）、中等大变形（Ⅱ级）和强烈大变形（Ⅲ级），大变形等级与各评价指标的关系如表2所示。

表2 大变形等级与各评价指标的关系Table 2 Relationship between rating and evaluation indexes of large deformation

2 组合赋权-理想点模型

2.1 组合赋权确定指标权重

2.1.1 层次分析法（AHP）

首先，通过对影响围岩大变形评价的7个因素进行层次划分，确定相应的目标层、准则层和子准则层。其次，采用SAATY[43]提出的9级标度法构建每一层对上一层的判断矩阵，求得最大特征值以及特征向量，归一化处理后得到各级影响因子的权重。最后，进行一致性检验，当判断矩阵的随机一致性比例小于0.1时，认为层次分析法计算的指标权重系数是合理的。否则，需调整判断矩阵的评价因子，重新计算直至一致性比例满足要求为止。

2.1.2 熵权法（EWM）

熵权法的基本思路是利用评价指标的熵来计算各指标权重系数，是一种客观分析方法[44]。本文利用其对大变形评价指标进行客观赋权，其评价指标分为“效益型”和“成本型”2种，经量纲归一化处理后，计算可得评价指标的权重系数。

2.1.3 组合赋权法

如前所述，层次分析法根据专家的主观经验确定判断矩阵，熵权法的评价过程则完全依赖客观数据。为了既反映研究人员在野外地质勘察阶段对隧道地质条件及围岩大变形的直观认识，又不失客观数据的典型规律及真实性，本文引入距离函数判别法[45]，耦合层次分析法和熵权法来综合确定大变形评价指标的权重系数。

假设组合权重为wi，层次分析法和熵权法的指标权重分别为wia和wie，其对应的分配系数依次为α和β，二者的距离函数M可以表示为

为了让层次分析法和熵权法之间的差异程度以及各分配系数间的差异程度保持一致，需使用相应的定解和约束条件[45]：

2.2 构建理想点评价函数

在本文提出的挤压性围岩大变形预测模型中，理想点评价指标分为增长型、减少型和区间型。

式中：fi*（+）为第i个评价指标的理想值；Vil和Viu分别为第i个评价指标理想区间的最小和最大临界值。

理想点评价函数是通过计算评价对象与理想点的距离来作为综合评价的依据，距离越小，说明评价对象与理想点越接近。本文采用闵可夫斯基距离函数[26,46-47]计算评价对象与理想点的距离D：

式中：fi（x），fi*（+），fi*u和fi*l分别为第i个指标的评价值、理想值、上限值和下限值。当H取1，2和∞时分别代表曼哈顿距离、欧氏距离和切比雪夫距离。距离函数（相似性度量）是表示2个特征向量相似度的一种度量方式，选择恰当的相似性度量函数至关重要。为了方便计算和对比分析，在本文的实际大变形预测中，分别选取H为1和2对挤压性围岩大变形进行评价。

3 工程案例验证

3.1 隧道工程大变形数据

为了验证本文构建的组合赋权-理想点法模型预测挤压性围岩大变形等级的可行性和准确性，统计整理了近年来国内典型深埋长大隧道的挤压性围岩大变形资料。考虑到岩体强度主要与岩石抗压强度、岩体完整性和地质构造影响程度等有关，根据地质构造对岩体强度影响程度[17]，计算确定其岩体强度。由于围岩级别、地质构造和地下水特征在大变形分级时给出的数值都存在一个范围，这给理想点法定量预测评价挤压性围岩大变形等级带来不便，故初步采用取平均值的方式得到确定数值。各隧道工程大变形分析数据经处理后如表3所示。

表3 处理后的隧道工程大变形分析结果Table 3 Large deformation analysis results of tunnel projects after treatment

3.2 构建评价指标体系及理想点决策矩阵

从表2和式（3）可知：在无大变形和强烈大变形区间范围内，岩石抗压强度、围岩强度应力比和弹性模量为“效益型”指标，围岩洞壁最大主应力、围岩级别、地质构造和地下水为“成本型”指标；在轻微大变形和中等大变形区间范围内，7项指标均为“区间型”指标。由于无大变形和强烈大变形的理想区间较大，评价指标无最优值。为了确保进行正确的围岩大变形分级，本文在真实的理想点附近选择一个“近似理想点”对其进行等效代替，根据轻微和中等大变形各个评价指标的区间分布情况，在无大变形和强烈大变形的理想区间补充相应的下限值和上限值以确定其“近似理想点”，如表4所示。

表4 修正后大变形等级与各评价指标的关系Table 4 Modified relations of large deformation intensity and evaluation index

根据式（3）及表4，确定7个理想点评价指标在不同大变形等级下的具体值，从而构建出挤压性围岩大变形预测模型的理想点决策矩阵Fi*（+）：

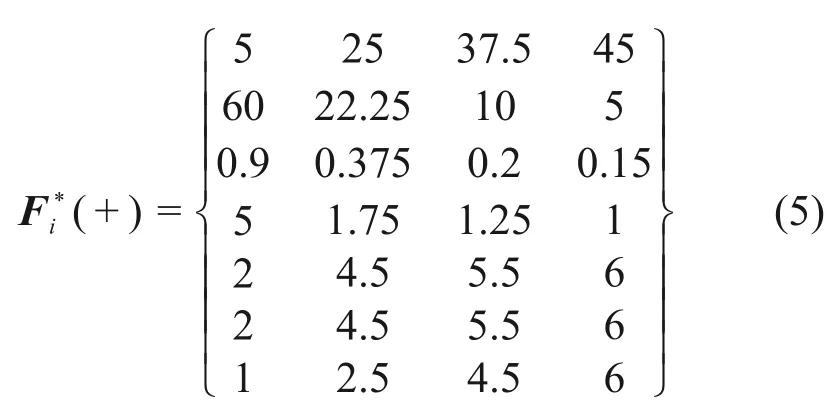
3.3 确定评价指标权重

根据2.1.1 节的分析，建立挤压性围岩大变形的层次结构模型（图8）。按照层次分析法中的9 级标度法，对准则层的3 个影响因子进行重要性评价，构建准则层对目标层的判断矩阵，并进行一致性检验，从而确定准则层中岩性条件、应力条件和围岩性质的权重系数依次为0.261，0.411 和0.328。同理，可得子准则层中的各指标权重系数。根据熵权法基本原理，结合表3中隧道工程的大变形分析数据，计算得到各指标的客观权重系数wie。最后，引入距离函数判别法，通过组合赋权规则确定层次分析法和熵权法的权重分配系数依次为0.556 和0.444，将主观权重wia、客观权重耦合并确定隧道案例各评价指标的组合赋权权重wi，具体结果如表5所示。

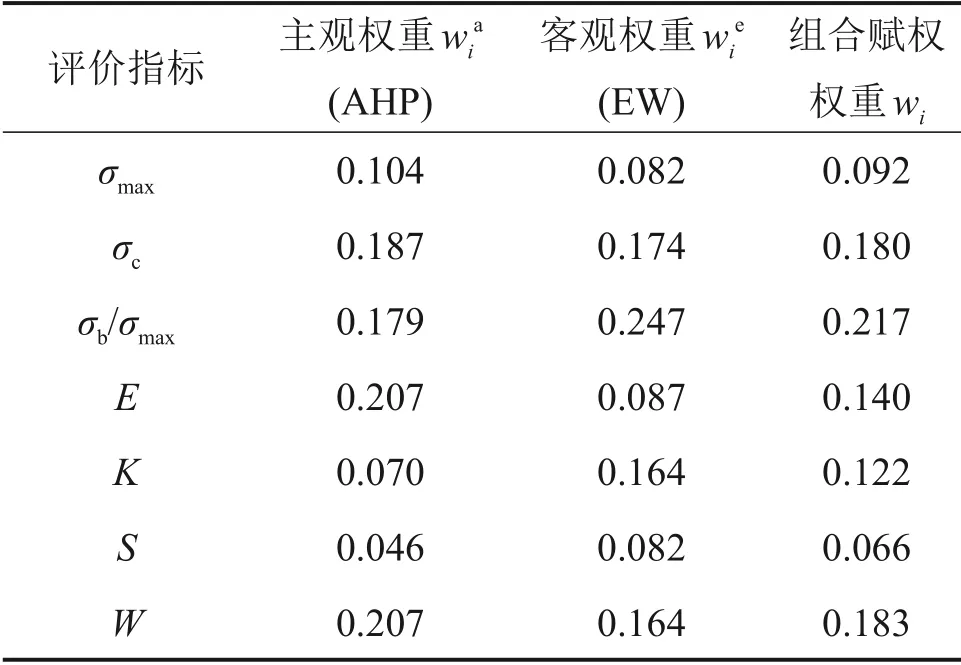
表5 大变形各评价指标权重Table 5 Weight of each evaluation index of large deformation

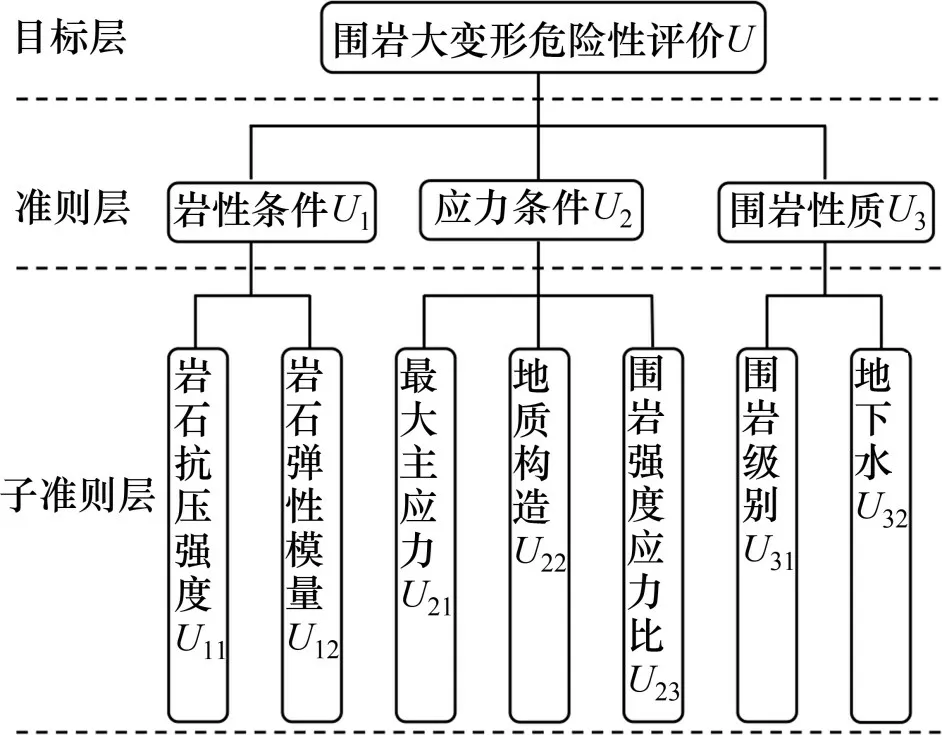
图8 围岩大变形评价层次结构模型Fig.8 AHP model of large deformation assessment of surrounding rock

3.4 挤压性围岩大变形预测结果

为了对该模型进行可靠性检验，将表3中的结果代入组合赋权-理想点大变形预测模型，并将评价结果与实际大变形等级进行比较，如表6所示。由表6可知：当H=1 时，准确率仅有27.3%，判别结果和实际大变形等级相差较大（图9）。从式（4）可知：当H=1 时，大变形各评价指标与理想点的距离可能为负，也可能为正，综合加权后可能会减少或增大评价指标与理想点之间的距离，从而导致预测结果偏离实际情况。当H=2 时，各大变形评价指标与理想点的距离均为正，总体变异性不明显，除第11 组都汶公路龙溪隧道预测为轻微大变形（实际为中等大变形），其余10组预测结果与实际情况吻合，准确率达90.9%。从结果上可以判定，选用欧式距离作为本文预测模型的距离函数可能更合适。此外，第11 组预测结果与实际情况存在一定出入，究其原因，可能是前期地质勘察阶段该区段存在未查明的地质构造异常带或其他基本参数离散性较大，导致判别结果偏危险，需要进一步核实。因此，在隧道掘进施工过程中，建议及时开展现场和室内相关试验，加强监控，将综合实测数据代入大变形预测模型中，不断修正和调整大变形风险等级。