基于节段同步测力的桁架梁二维气动导纳直接识别

2021-11-25史明杰严磊何旭辉张裕名邹云峰

中南大学学报（自然科学版） 2021年10期

史明杰，严磊,2,3，何旭辉,2,3，张裕名，邹云峰,2,3

（1.中南大学土木工程学院，湖南长沙，410075；2.中南大学高速铁路建造技术国家工程实验室，湖南长沙，410075；3.中南大学轨道交通工程结构防灾减灾湖南省重点实验室，湖南长沙，410075；4.中国电建集团中南勘测设计研究院有限公司，湖南长沙，410014）

在桥梁抖振分析中，气动导纳是一个重要的气动参数。它是脉动风到气动力的传递函数，可反映作用于桥梁上气动力的非定常特性。基于薄翼理论和势流理论，SEARS[1]推导了二维薄机翼在展向完全相关正弦阵风中的气动力，给出了薄机翼升力气动导纳的函数表达式即Sears函数。Sears函数是完全二维的，没有考虑脉动风的三维空间分布特性，而实际上湍流具有三维特性，沿展向不完全相关。为了考虑脉动风的展向变化，LIEPMANN[2]引入二波数气动导纳，提出了三维荷载模型。基于升力面理论，GRAHAM等[3-4]给出了任意水平湍流场中无限展长机翼的二波数气动导纳的数值解即Graham函数。

LI 等[5-8]提出了三维二波数气动导纳的通用识别法，并用该方法识别了典型桥梁断面的气动导纳。由LI 等[6-7]提出的气动导纳闭合表达式可知，三维二波数和三维一波数气动导纳可以通过反映湍流三维特性的展向修正项修正二维气动导纳获得，即一旦知道桥梁断面的二维气动导纳，就可以直接计算三维二波数气动导纳和三维一波数气动导纳，因此，桥梁断面二维气动导纳的识别至关重要。

目前识别桥梁断面二维气动导纳的方法主要有2种：间接识别法和直接识别法。其中，间接识别法是基于LI等[5]提出的三维二波数气动导纳通用识别法，令识别的三维二波数气动导纳的展向波数为0，使其退化为二维气动导纳。该方法的精度依赖于抖振力相干函数经验模型，而且在实际频谱分析中存在频率难以直接取到0的问题。直接识别法又分为2种，其中一种是通过主动发生装置在风洞中直接生成理想二维风场，从而达到识别二维气动导纳的目的。例如JANCAUSKAS 等[9-12]利用振动翼栅、主动格栅和主动多风扇风洞实现了不同断面的二维气动导纳识别。尽管这种直接识别法的理论简单，但是由于理想二维风场难以在传统风洞中产生，而且一次试验只能得到1个频率点的二维气动导纳，因此，该方法的实际应用较少。MASSARO 等[13]指出对于自由流中的薄机翼，当展弦比（即试验模型长度与结构特征尺度的比）足够大时，展向波数对气动导纳的影响可以忽略，片条假设成立。为此，LI等[14]提出了一种基于节段模型整体测力试验的二维气动导纳近似识别法，LI等[15-17]利用该方法识别了典型桥梁断面的二维气动导纳。YANG等[18]提出了基于节段模型测压试验的矩形断面二维气动导纳直接识别法。

节段模型整体测力试验是一种常用的风洞试验方法，其操作简单，便于应用[19]。但为了使片条假设成立，节段模型的断面尺寸需足够小，展向长度需足够大，从而导致节段模型的整体刚度下降，天平-模型系统的自振频率降低，气动导纳的识别精度受到影响；同时，小尺度节段模型（包括桥梁附属设施）的制作精度难以保证。基于测压试验的二维气动导纳识别精度高于基于整体测力试验的识别精度，但测压试验[20]需要布置测压孔来测量桥梁气动力，因此，难以适用于桁架梁以及桥梁附属设施气动力的测量。

为了同时测量桥梁断面的气动力以及抖振力展向相关性，YAN等[21-22]研发了箱梁多片条同步测力新技术，ZHONG 等[8,23]提出了桁架梁多节间同步测力技术。为了避免上述整体测力和测压试验在桁架梁二维气动导纳识别中存在的缺陷，基于张裕名[24]开发的桁架梁节段同步测力技术，本文提出桁架梁二维气动导纳的直接识别法。应用此方法识别桁架梁的升力二维气动导纳，并探究湍流场非各向同性成分对二维气动导纳识别的影响，最后将该方法推广到其他桥梁断面的二维气动导纳识别。

1 数学模型

1.1 风谱模型

一般而言，风洞试验通常采用均匀格栅产生近似各向同性湍流。为了描述各向同性湍流，采用Von Kármán 风谱模型[18]，其顺流向和竖向湍流的一波数和二波数风谱的表示式如下：

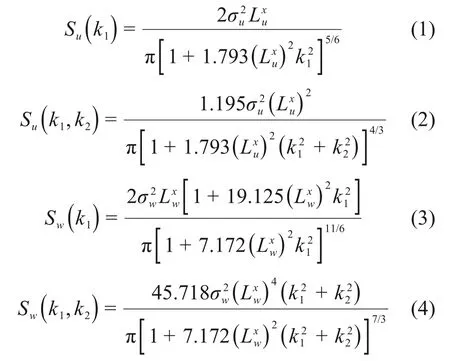
式中：k1和k2分别为顺流向和展向波数（即2π长度内的波周数目），k1=k2=2πf/U；f为工程频率，Hz；U为来流平均风速，m/s；u和w分别为顺流向和竖向湍流，m/s；σ2u和σ2w分别为湍流u和w的方差，m2/s；Lxu和Lxw分别为湍流u和w的顺流向（x方向）湍流积分尺度，m，并满足Lxu=2Lxw；Su(k1)和Su(k1,k2)分别为湍流u的一波数和二波数风谱；Sw(k1)和Sw(k1,k2)分别为湍流w的一波数和二波数风谱；n和a分别为控制形状和尺度的参数。对于各向同性湍流，湍流积分尺度Lxu和参数a有如下关系：

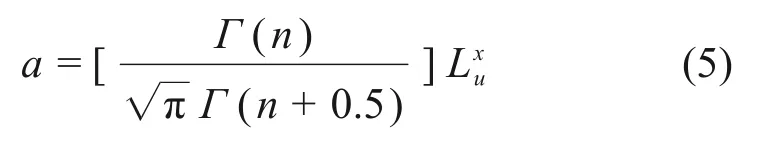
式中：n=1/3；a≈1.339Lxu=2.678Lxw；Γ为伽马函数。

需要注意的是，式（2）和（4）仅在各向同性湍流场中才能适用。受李少鹏[25]研究尖塔湍流场非各向同性湍流分量相关性的成果启发，对于湍流场中的非各向同性成分，可以采用以下方法进行修正：

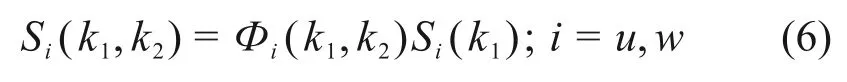
式中：Фu（k1,k2）和Фw（k1,k2）分别为顺流向和竖向湍流二波数相干函数，由一波数相干函数进行傅里叶变换所得。

采用JAKOBSEN[26]提出的相干函数经验模型描述湍流的相干性。为了方便应用，将其参数进行量纲一处理[6]，得到顺流向和竖向湍流的相干函数Cohi为：

式中：Δy为展向间距，m；k*1为顺流向单位长度内的波周数目，k*1=f/U；ci,1，ci,2和ci,3（i=u,w）为待拟合参数。因此，改进Jakobsen经验模型的顺流向和竖向湍流二波数相干函数为

式中：k*2为展向单位长度内的波周数目，k*2=f/U。

将二波数风谱沿k2积分即可得到一波数风谱，于是顺流向和竖向湍流的一波数与二波数风谱的关系为

1.2 桥梁断面二维气动导纳识别

以升力为例，对一般桥梁断面二维气动导纳识别法进行推导。考虑到桁架梁沿展向各断面外形不同，应用等效断面的概念[27]，假设桁架梁沿展向每个断面是相同的。

借助LI 等[15]推导的桥梁节段两波数抖振力谱模型，单位长度桥梁节段两波数抖振升力谱SL(k1,k2)表达式为

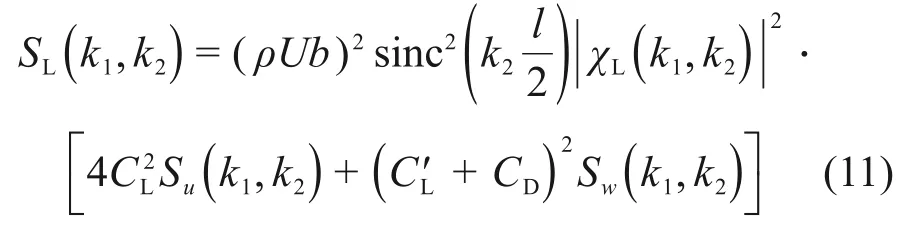
式中：ρ为空气密度，kg/m；b为断面半宽，m；l为节段长度，m；sinc为辛格函数；为等效三维二波数气动导纳函数（以下简称三维二波数气动导纳）；CL和CD分别为桥梁断面升力系数和阻力系数，特征尺寸均为断面宽度；CL′ 为升力系数对风攻角的导数。

将式（11）对k2积分，得到单位长度桥梁节段一波数抖振升力谱SL(k1)：

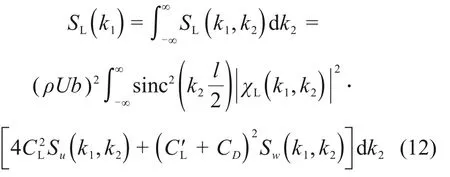
相距Δy的2 个桥梁节段的抖振升力互谱SL(k1,Δy)为

式中：i为虚数单位。

三维二波数气动导纳和断面二维一波数气动导纳有如下关系[6,7,21]：

相距Δy的2 个桥梁节段抖振升力相干函数CohL(k1,Δy)可以定义为

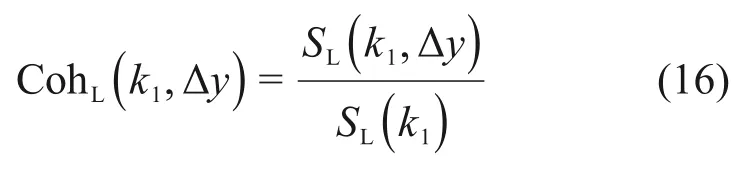
将式（12）～（15）代入式（16）可得到相距Δy的2 个桥梁节段间的抖振升力相干函数：

相距Δy的2个桥梁节段间的气动力相关性与相距Δy的2个桥梁断面（桥梁节段长度l趋近于0）间的气动力相关性可认为相同[23-24]，即展向间距相同的节段抖振升力相干函数CohL(k1,Δy)与断面抖振升力相干函数CohL,sec(k1,Δy)相同。所以，桥梁节段抖振力相干函数也可以表示为

值得说明的是，只要用式（18）拟合桥梁节段抖振升力相干函数试验值即可得到a1，a2，a3这3 个待拟合参数，从而获得气动导纳修正项为二维气动导纳的识别提供必要参数。

另外，单位长度桥梁节段抖振升力一波数谱还可以表示为

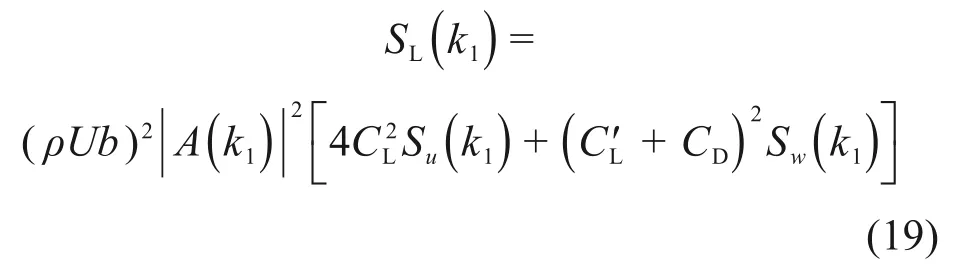
结合式（12），（14）和式（19），二维气动导纳表示为

式中：ψ为三维效应因子，包含了流场和气动导纳本身的三维特性，其表达式为

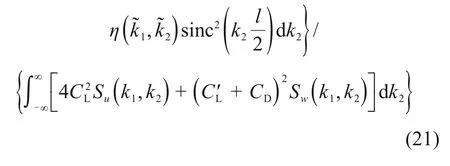
2 平潭海峡公铁两用大桥概况

平潭海峡公铁两用大桥全长16.34 km，包括跨越元洪航道、鼓屿门水道和大小练岛水道的3座大跨度钢桁梁斜拉桥。主梁采用倒梯形的桁架梁形式，见图1，主梁的宽度为36.8 m，高度为13.5 m，每个节间长14.0 m。本文以该桁架梁施工阶段的断面为研究对象，采用提出的二维气动导纳直接识别法识别该断面的二维气动导纳。

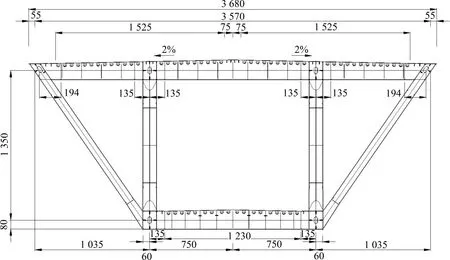
图1 钢桁梁断面图Fig.1 Cross-section of truss girder

3 风洞试验

试验[24]在中南大学风洞实验室高速试验段进行，高速试验段宽为3 m、高为3 m、长为15 m。湍流场利用格栅产生，正方形格栅网格边长为0.4 m，5 根横向板条的宽度均为0.14 m，5 根竖向板条宽度分别为0.14，0.21，0.14，0.21和0.14 m，板条的厚度均为0.01 m，节段模型中心到上游格栅断面的距离为9 m。

节段模型包含测力节段和补偿段2部分，几何缩尺比为1∶80。测力节段高为0.191 m，长为0.175 m，宽为0.460 m。测力节段与天平连接处用碳纤维板制作，测力节段桥面板为2 mm厚巴尔沙木板，其余部分采用1 mm 厚的巴尔沙木板。图2所示为测力节段实物图和测力节段与天平连接图。试验共设置4 种展向间距，分别为0.175，0.350，0.525 和0.700 m，其中，间距Δy=0.35 m的试验模型见图3。采用4个天平对各种展向间距时的2个桁架梁节段进行同步测力，每个测力节段通过2个天平固定在各自一侧的补偿段上，两侧补偿段则通过直径为8 mm、距模型表面10 cm 的圆杆相互连接，使中间补偿段和两侧补偿段构成一个整体。为了进一步提高模型整体刚度，用8 根钢丝上下拉住模型，见图3。

图2 测力节段及模型与天平连接细节Fig.2 Force-balance measurement segment and connection details between measurement segment and force balance

采用澳大利亚Turbulence Flow 公司生产的Series100 系列四孔眼镜蛇探头测量风速。该探头能测量空间某点处3 个脉动风速分量和局部静压，其频率测量范围为0～2 000 Hz，能在±45°圆锥体范围内测量2～40 m/s 的瞬时风速。试验中该眼镜蛇探头采样频率设置为200 Hz，采样点数为65 536个。采用美国ATI 公司生产的高频动态天平（Mini40）测量节段抖振力，其直径为40 mm，厚度为12.2 mm，采样频率同样设置为200 Hz，采样点数为65 536 个。试验时，同步测量不同展向间距时的2 个测力节段的抖振力以及相应来流风速（见图3）。试验风速设置为10 m/s，实际试验平均风速为9.568 m/s，雷诺数（以模型宽度0.46 m 为特征长度）为297 384。风攻角设置为0°，模型中心轴线与来流湍流的流向垂直。

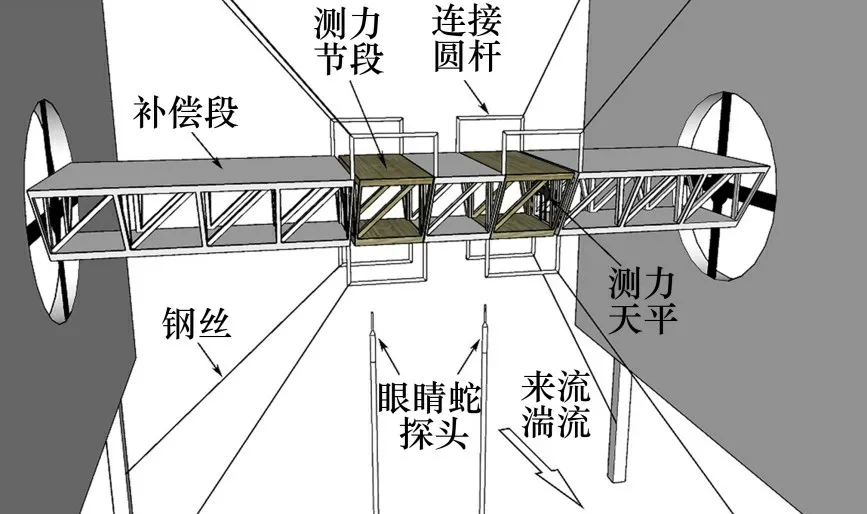
图3 节段模型同步测力试验示意图（Δy=0.35 m）Fig.3 Scheme of synchronous segmental force-balance measurement（Δy=0.35 m）

尽管连接圆杆提高了模型整体性和刚度，但其对模型三分力系数以及流场的影响尚不明确。图4所示为均匀流中间距Δy=0.175 m 的节段模型同步测力试验图。图4（a）所示为无连接圆杆的模型，图4（b）所示为有连接圆杆的模型。通过试验获得这2种模型布置下的三分力系数（攻角α为-12°～+12°，变化间隔为2°），如图5所示。

图4 有无连接圆杆节段模型同步测力试验（Δy=0.175 m）Fig.4 Synchronous segmental force-balance measurement without or with connecting cylindrical bar（Δy=0.175 m）

由图5可知：有无连接圆杆的模型三分力系数趋势一致；有连接圆杆的模型三分力系数与无连接圆杆时相比，阻力系数略微降低，升力系数在-4°攻角以上几乎一致，升力矩系数略微增加。因此，加装连接圆杆对三分力系数以及流场的影响很小。

图5 桁架梁三分力系数[24]（Δy=0.175 m）Fig.5 Aerodynamic force coefficients of truss girder[24]（Δy=0.175 m）

4 结果与讨论

4.1 流场特性

试验格栅湍流场的湍流度和湍流积分尺度如表1所示，其中，Iu和Iw分别为顺流向和竖向湍流的湍流度，Iu=σu/U，Iw=σw/U，%。

表1 湍流场特性Table 1 Characteristics of turbulent flow

为了获得风谱实测值，采用Pwelch 法进行功率谱分析。将脉动风速时程的65 536 个数据按2∶1重叠分段，共分成31 段，每段为1 个子样本，每个子样本数据点数为4 096 个，相邻2 个子样本重叠数据点数为2 048个。由于截断时域信号会引起频域信号泄漏，故采用加Hamming 窗的方法减少泄漏。实测一波数风谱和Von Kármán 拟合风谱见图6。

图6 实测和拟合风谱Fig.6 The measured and fitted spectrum of turbulent flow

从图6可见实测一波数风谱与Von Kármán 谱吻合较好。另一方面，若湍流场特性满足Iu=Iw，则来流湍流场可视为各向同性湍流，并可将一波数风谱拟合参数直接代入式（2）和（4）求得二波数风谱。而由表1可知，Iu=1.35Iw，Lxu=1.69Lxw，故无法直接利用式（2）和（4）。因此，有必要修正来流湍流场中的非各向同性成分。

根据1.1 节中湍流场非各向同性成分修正方法，用式（7）拟合实测湍流相干函数，获得c1，c2，c3这3 个待拟合参数，然后根据式（9）和（6），依次得到顺流向和竖向湍流的二波数相干函数和二波数风谱。基于改进Jakobsen相干函数模型的二波数风谱如图7所示。由图7可知，顺流向和竖向湍流的能量基本集中在k1＜2.17和k2＜2.17范围内。

图7 基于改进Jakobsen相干函数模型的二波数风谱Fig.7 Two-wavenumber wind spectrum based on improved Jakobsen’s coherence function model

图8所示为不同展向间距时的湍流积分尺度和湍流度。由图8可知：顺流向和竖向湍流的湍流积分尺度和湍流度的实测值在不同展向间距时均比较接近，因此，可以认为来流湍流场满足空间均匀性的要求。

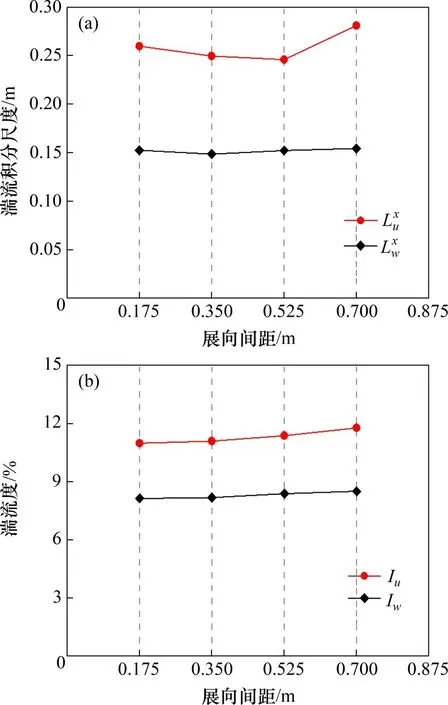
图8 不同展向间距时的湍流积分尺度和湍流度Fig.8 Turbulence integral scale and turbulence intensity at different spanwise spacings

4.2 单位长度抖振升力谱

利用天平所测的抖振力时程数据，对Δy=0.35 m（见图3）的节段模型抖振力采用与风谱相同的方法进行谱分析。图9所示为单位长度桁架梁节段的抖振升力谱。

对比图9和图6可知，抖振升力谱的峰值对应的波数（k1≈1.60）小于风谱的峰值对应的波数（顺流向风谱为k1≈3.66，竖向风谱为k1≈4.49），说明在来流湍流与桥梁相互作用过程中，能量从高波数向低波数转移。因此，从这个角度看，气动导纳可视作一个低通滤波器。

图9 单位长度抖振升力谱Fig.9 Buffeting lift spectrum per unit length

4.3 抖振力相干函数

根据图5中有连接圆杆模型的三分力系数，风攻角为0°的桁架梁三分力系数及其导数见表2。

表2 桁架梁三分力系数及其导数Table 2 Aerodynamic force coefficients of truss girder and their slopes

根据式（18）所示节段抖振力相干函数模型，拟合节段抖振升力相干函数实测值，以获得气动导纳修正项的拟合参数a1，a2和a3。试验有4种展向间距的节段抖振升力相干函数实测值，故共有15种展向间距相干函数实测值的组合（见表3）可以用于拟合，分别是组合1*，2*，3*，4*，1*&2*，1*&3*，1*&4*，2*&3*，2*&4*，3*&4*，1*&2*&3*，1*&2*&4*，1*&3*&4*，2*&3*&4* 和1*&2*&3*&4*。因此，在识别二维气动导纳时，需检验识别结果是否受展向间距组合选取的影响。

表3 15种节段抖振升力相干函数组合Table 3 15 combinations of segmental buffeting lift coherence function

图10所示为所有展向间距组合下的抖振升力相干函数实测与拟合结果。

从图10可知，所有展向间距组合的抖振升力相干函数的拟合值与实测值总体上较吻合。拟合结果具有一定规律性，且可以分为3类：A类，即组合1*；

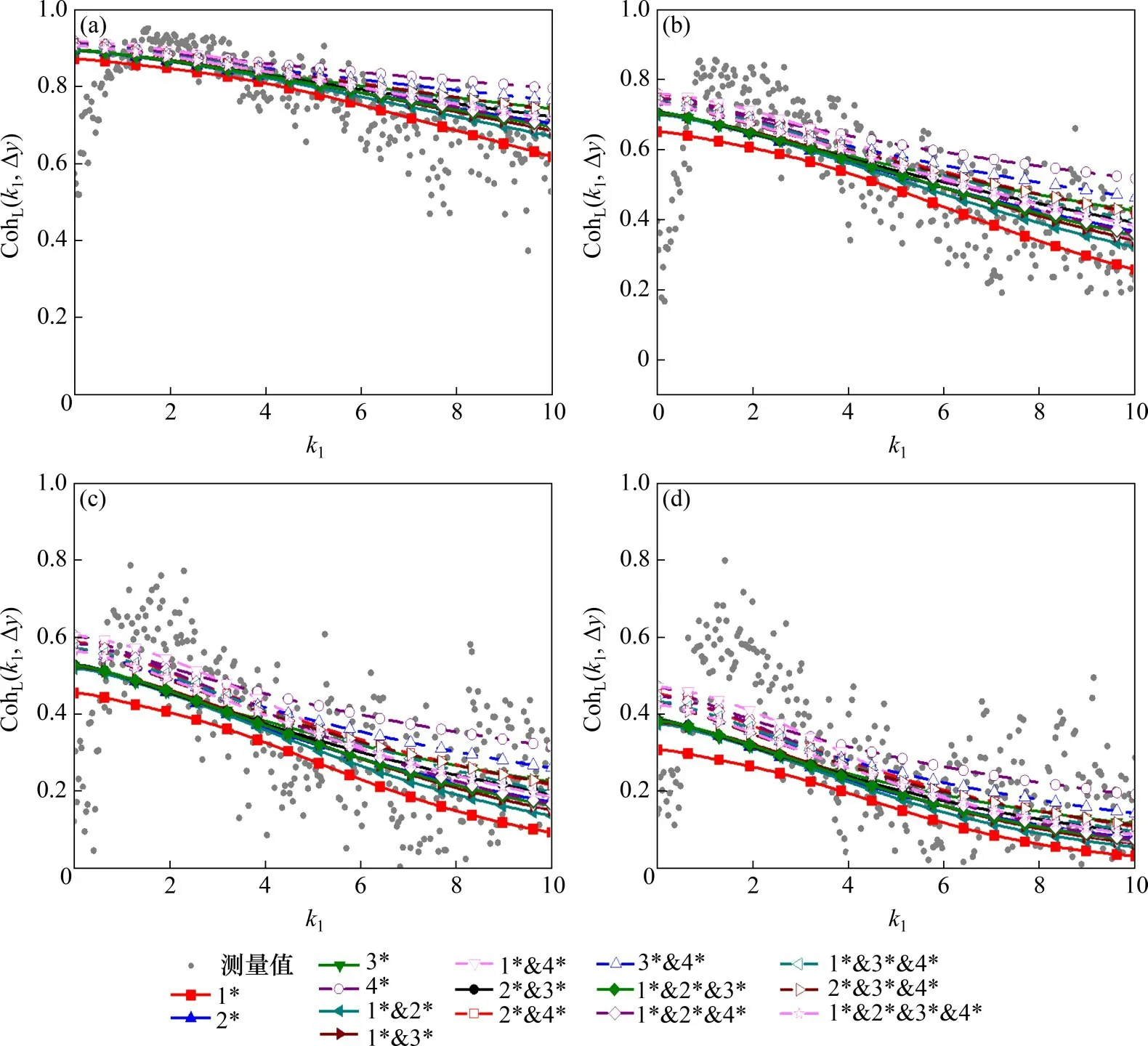
图10 节段抖振升力相干函数与k1的关系Fig.10 Relationship between segmental buffeting lift coherence function and k1

B 类，即组合2*，3*，1*&2*，1*&3*，2*&3*和1*&2*&3*；

C 类，即组合4*，1*&4*，2*&4*，3*&4*，1*&2*&4*，1*&3*&4*，2*&3*&4* 和1*&2*&3*&4*。在15 个间距组合下的节段抖振升力相干函数拟合结果中，C类最大，A类最小，B类居中。在低波数（k1＜4 范围内）有较明显的分类现象，且展向间距越大，分类现象越明显；随着波数增加，部分B类和C类的拟合值重叠，分类程度减弱，但A类始终最小。

总体而言，本文采用的节段抖振升力相干函数模型较好地描述了桁架梁的升力相干函数特性，能够用于二维气动导纳的识别。

4.4 桁架梁二维气动导纳

将二波数风谱、气动导纳修正项代入式（21）得到三维效应因子，将实测一波数抖振力谱和一波数风谱代入式（19）得到三维气动导纳，最后根据式（20）直接获得桁架梁的二维气动导纳。基于上述15种展向间距组合的桁架梁二维气动导纳识别值如图11所示，其中图11（a）考虑了来流湍流场非各项同性成分的修正，即由式（6）求得二波数风谱；图11（b）未考虑来流湍流场非各项同性成分的修正，即直接采用式（2）和（4）求得二波数风谱。

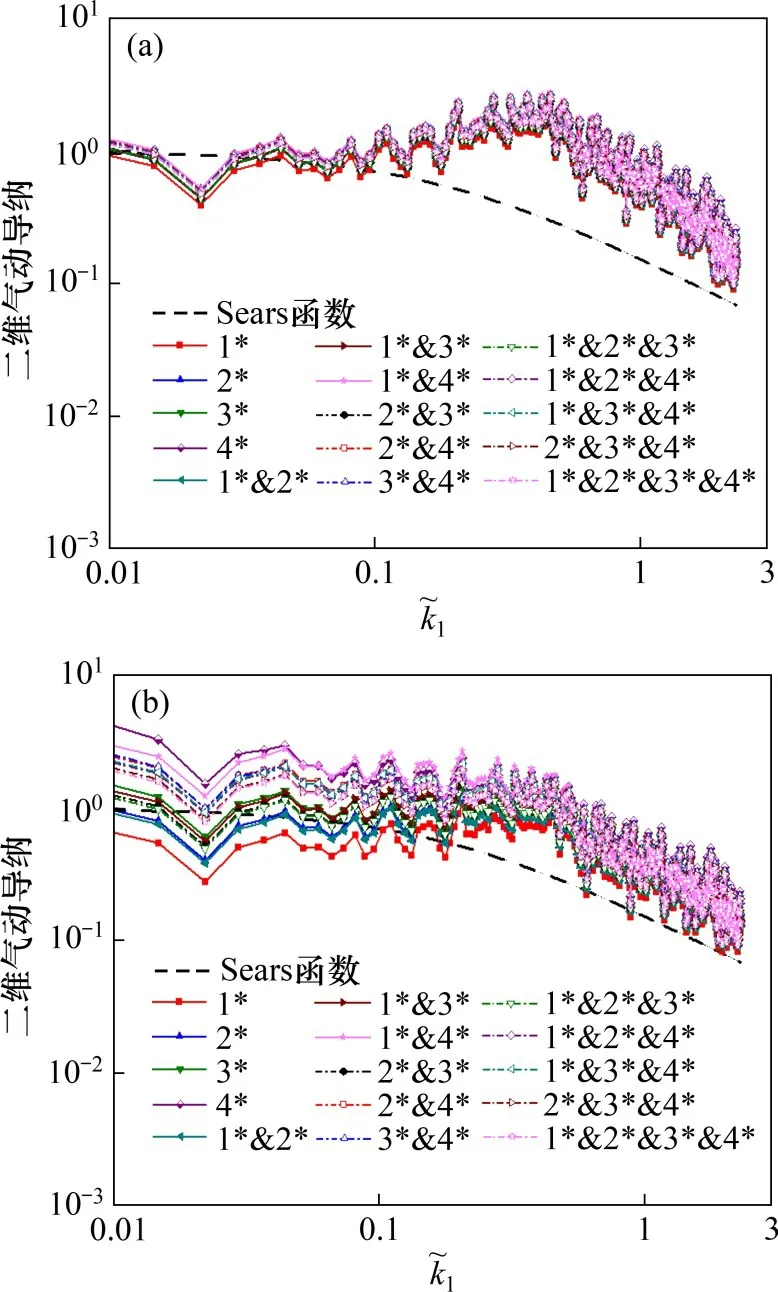
图11 15个二维气动导纳识别值Fig.11 15 two-dimensional aerodynamic admittances

由图11可知，考虑来流湍流场非各项同性成分修正的15 个二维气动导纳识别值基本一致，二维气动导纳的识别基本不受抖振力相干函数拟合时展向间距组合选取的影响，然而，未考虑来流湍流场非各项同性成分修正的15 个二维气动导纳识别值在低频差异很大。因此，识别二维气动导纳时有必要对非各向同性湍流场的各湍流分量进行修正。

图12所示为桁架梁三维效应因子，图13所示为桁架梁一波数气动导纳。

图12 桁架梁三维效应因子Fig.12 Three-dimensionality effect factor of truss girder

图13 桁架梁一波数气动导纳Fig.13 One-wavenumber aerodynamic admittances of truss girder

由图13可知二维气动导纳试验值大于三维气动导纳试验值，这与三维效应因子ψ（存在三维效应）有关。在图12所显示的频率范围内，三维效应因子较小，没有超过0.275，因此，根据式（20），二维气动导纳大于三维气动导纳。升力二维气动导纳试验值在k˜1＜0.1 范围内接近于1，然后，随着频率增加，二维气动导纳开始增加，到达峰值后迅速衰减。升力二维气动导纳试验值在高频段大于相应Sears 函数值。LI 等[16]认为钝体桥梁断面升力的主要来源有2个：一是断面周围风压的综合作用，这一部分对来流湍流场特性比较敏感，并随着频率增加迅速降低；另一部分则是钝体流动分离形成的剪切层再附的压力效应。JANCAUSKAS 等[9]指出第二部分升力对来流湍流场特性不敏感，只取决于流动分离造成的加速效应，因此，低频范围内由第2种机理产生的升力更接近于准定常值，从而导致二维气动导纳在低频段更接近于1。桁架梁升力二维气动导纳试验值以及相应的三维气动导纳试验值出现峰值的原因可能是：通透的桁架梁有较多的弦杆，来流风流经桥梁断面时，会在弦杆处产生较多漩涡，由此产生较强的三维效应（对应图12在0.1＜＜1频率范围内较小的三维效应因子）；由于测试来流湍流不包括特征湍流部分，因此，二维气动导纳试验值在0.1＜＜1 频率范围内大于1。该现象与ZHONG等[8,28]识别的气动导纳值趋势类似。

对比前人研究的矩形断面桁架梁的二维气动导纳[16]，本文识别的桁架梁二维气动导纳试验值与其存在一定的差异。一方面，LI[16]所采用的桁架梁是矩形断面，而本文是倒梯形断面，气动外形不同导致气动导纳识别值不同。另一方面，LI等[16]基于节段模型整体测力试验，本文基于节段模型同步测力试验，试验方法不同也会造成一定的误差。因此，2 种桁架梁二维气动导纳试验值存在一定差异。