基于熵产理论的超低扬程双向卧式轴流泵装置飞逸特性

2021-11-25黄佳程

农业工程学报 2021年17期

许哲，郑源,，阚阚，黄佳程

（1. 河海大学水利水电学院，南京 210098；2. 河海大学能源与电气学院，南京 210098）

0 引言

卧式轴流泵具有结构紧凑、安装及检修方便等优点，多用于平原地区的低扬程泵站，以满足灌溉、排水、防洪及调水等需求。近年来，随着南水北调东线工程稳步推进，泵站运行的安全稳定性得到越来越多的关注。当泵站机组遭遇断电事故，若出水流道侧闸门拒动而不能截断水流，水泵机组会进入水流倒流、叶片反转的水轮机工况。当叶轮转速增至最大转速时，水泵处于稳定飞逸状态，此时叶轮的最大转速称为飞逸转速。在飞逸过渡过程中，机组流道内将出现流态复杂、大尺度漩涡流动等不稳定现象，极易引发流场内部剧烈的压力脉动和周期性尾水涡带，威胁到机组的稳定运行。为了保证泵站的稳定运行和电站设备的安全，需要对机组的瞬态过程开展研究。

目前，针对水泵系统瞬态过程的研究，主要是基于一维特征线法（Method of Characteristics，MOC）的数值解法，优点是计算迅速和外特性模拟准确。在理论创新方面，Afshar等[1]提出了隐式特征线法，对管路系统中的阀门、蓄水池和泵等设备进行单元式定义，并推导相应的控制方程，与显示特征线法相比，计算得到的扬程与流量变化更加准确；Rohani等[2]基于隐式特征线法，提出了点隐式特征线法，进一步简化了计算量。在工程应用方面，葛强等[3]研究了灯泡贯流泵站在不同电机过载系数及不同叶片角度下的起动过程；余国锋等[4]研究了水轮发电机组导叶按线性规律开启的过渡过程；黄晨等[5]研究了三机式抽水蓄能电站在不同调速器转速整定值下的停泵过程。一维数值模拟能够快速准确地得到水泵系统的外特性参数变化过程，但不能反映机组内部流态的瞬态特性。近年来，随着现代数值方法的快速发展，计算流体动力学（Computational Fluid Dynamics, CFD）已成为水力机械过渡过程数值模拟的有力工具[6-8]。李琪飞等[9]对水泵水轮机飞逸过程进行模拟，发现无叶区高速水环是导致随机脉动与能量损失的原因；Fortin等[10]对水轮机飞逸过程中叶片上的压力进行模拟，并通过模型试验对压力结果进行验证；罗兴锜等[11]分析了灯泡贯流泵飞逸时叶片进口相对液流角与速度矩的演变规律；陈会向等[12]研究了桨叶调节方式对轴流式水轮机甩负荷特性的影响。

在分析机组运行过程中的水力损失时，常通过效率公式来间接评估总水力损失，不能直观判断不同部位能量损失的来源及具体分布。与此同时，当机组处于瞬态过程中时，各参数尚在变化之中，因此常规的计算方法不能得到准确的水力损失。如今越来越多的学者开始关注熵产与水力损失的联系，即通过计算内能耗散来评估水力损失，但目前熵产理论在水力机械方面的应用仍然较少。Kock等[13]基于雷诺时均方程首次提出熵产率的计算公式；张翔等[14]提出了壁面摩擦损失的计算方法；Yu等[15]推导了空化熵产率的公式。随着熵产理论的发展，越来越多的学者开始运用熵产理论来分析流动过程中的能量损失。在优化设计方面，王威等[16-18]运用熵产理论对翼型、离心风机及轴流式反向发电机组进行了优化设计，提高了能量的利用效率。在飞逸过程的模拟方面，Zhou等[19-20]基于熵产理论对抽水蓄能机组及离心泵的断电飞逸特性进行分析。以上结果均表明，熵产理论可定量描述各过流部件内的能量损失。

以往水力机械飞逸过程的研究中，研究对象大多局限于水力机械装置本身，未涉及上下游水域的演变过程；与此同时，研究方法也少有涉及熵产理论，少有从能量损失的角度来阐述机组的瞬态变化过程。超低扬程的双向泵具有双向输水能力，同时也具有双向飞逸的风险，而目前针对双向飞逸过渡过程的研究较少。本文采用熵产理论分析机组飞逸过程的演变规律，并对比正反向飞逸工况下能量损失；并通过模型试验来验证三维模拟及熵产理论的准确性；最后，以正向飞逸工况下叶片展开面处漩涡与熵产率的分布为例，分析能量损失与流场漩涡的关联，以期为机组安全稳定运行提供参考。

1 数值计算方法

1.1 控制方程与湍流模型

卧式轴流泵装置内水流的流动受质量守恒定律和动量守恒定律的约束，为简化计算，本文采用雷诺时均化的方程形式。上下游计算域自由液面附近的水和空气并不混掺，故可用流体体积函数（Volume of Fluid，VOF）来确定自由液面的位置及计算水气两相的体积分数，控制方程[6,11]如下：

连续性方程：

动量方程：

VOF方程：

剪切压力传输（Shear-Stress Transport，SST）k-ω[12]湍流模型修正了湍流黏度公式，可以更好地传递壁面处的剪切应力，有助于预测近壁区的流动，因此选择SSTk-ω湍流模型来封闭控制方程。

1.2 熵产理论

根据热力学第二定律，熵的微增量总是大于0。通过熵产理论可以对水泵飞逸过程中能量的耗散进行量化评估，如回流现象、压力脉动、尾水涡带、流动分离等会加剧能量的损耗。在机组飞逸的过程中，考虑到水的比容较大，可以认为机组飞逸过程中水的温度保持不变，因此不考虑传热引起的熵产。基于雷诺时均的湍流运动，熵产率（Entropy Production Rate, EPR）主要包含3项：1）由时均速度引起的单位体积熵产率，称为直接耗散项；2）由湍流脉动引起的单位体积熵产率，称为湍流耗散项；3）由壁面摩擦损失引起的单位面积熵产率，称为壁面耗散项。其中，单位体积总熵产率S˙D′[13]可表示为

式中tμ表示湍流动力黏度，Pa·s。

本文采用雷诺时均方法进行数值模拟，无法直接计算湍流耗散项。根据Kock等[13]提出的思想，当雷诺数趋向于无穷大时，可以将SSTk-ω湍流模型中的ω与脉动速度分量产生的熵产率关联起来，即

式中经验系数β通过直接数值模拟率定得到，β=0.09[13,21]；k表示湍动能，m2/s2；ω表示湍流涡黏频率，s-1。

根据张翔等[14]提出的壁面摩擦损失的计算方法，壁面耗散熵产WS可通过积分得到：

式中τw表示壁面剪切应力，Pa；uw表示壁面区第一层网格中心速度矢量，m/s；A表示计算域表面积，m2。

计算区域内由时均速度与脉动速度引起的熵产亦可通过积分获取，即

式中SD表示直接耗散熵产，W/K；S D′表示湍流耗散熵产，W/K；V表示计算域体积，m3。

各计算域内的总熵产S(W/K)为

1.3 算法实现

当水泵处于断电飞逸状态时，叶轮的转速受自身水力扭矩的控制，因此使用Fluent软件的自定义函数功能（User defined function, UDF）来控制叶轮的转速，力矩平衡方程[11]如下：

式中M是叶轮的总力矩，N·m，可通过UDF中的Compute_Force_And_Moment语句进行实时获取，机械摩擦力矩和转子风阻力矩较小，在总力矩中暂不考虑；J是转动惯量，kg·m2；n是转速，r/min。任意时刻下的叶轮转速离散化求解公式为

式中Mr表示第r时刻的总力矩，N·m；nr和nr+1分别表示第r和r+1时刻的转速，r/min；Δt表示第r和r+1时刻之间的间隔，s。

2 数值计算模型

2.1 几何模型

本文研究对象为超低扬程双向卧式轴流泵全过流系统，如图1所示。

泵段采用SZM35水力模型。叶轮直径为1.6 m，叶片数为4，导叶数为5，叶片安放角为-4°。在实际工程运行中，不同调水任务下的设计参数不同，正向工况下额定转速、设计流量及设计扬程分别为170 r/min、5.0 m3/s及0.91 m；反向工况下额定转速、设计流量及扬程分别为170 r/min、4.5 m3/s及1.03 m。这些参数均由实际工程需要确定。数值模拟的计算域包括叶轮、导叶、进出水流道及上下游计算域。为了保证模拟的真实有效性，以实际工程中泵装置的间隔距离、设计水位高度与开挖高度来确定上下游区域的宽度、自由液面与底面的位置等。

2.2 工况设置

本文考虑2种不同上下游水位工况下的飞逸过渡过程，正反向飞逸工况下的初始计算参数如表1所示。对于正向飞逸工况（Forward Runaway Condition, FRC），卧式轴流泵全过流系统的初始流场如图2a所示，水流依次流过直锥型进水流道、叶轮、导叶及S型出水流道；对于反向飞逸工况（Backward Runaway Condition, BRC），初始流场如图2b所示，水流依次流过S型进水流道、导叶、叶轮及直锥型出水流道。

表1 初始计算参数Table 1 Initial simulation parameters

在上述2种工况中，上下游计算域的进出口条件均为压力边界条件，并采用UDF功能定义压力边界条件，即压力沿水深变化，而非定值。采用Pressure-linked equation-consistent（SIMPLEC）算法来求解压力项和速度项，采用一阶隐式格式离散时间项，采用二阶迎风格式离散对流项和扩散项，时间步长设为0.001 s。

2.3 网格划分

本文采用ICEM软件对整个计算域进行结构化六面体网格划分，利用O形网格划分进出水流道，并对壁面处网格进行加密。y+值为第一层网格质心到壁面的无量纲距离[21]，以此可判别近壁区的节点分布是否合理。当壁面处y+值小于1.5时，可满足SSTk-ω湍流模型中低雷诺数k-ω在近壁处的要求。为了验证网格的独立性，采用网格收敛指数[22-23]（Grid Convergence Index，GCI）来评估网格方案引起的数值误差。本文选取3种由疏至密的网格方案，网格数量分别为547万、770万和984万，依据表1中的流量与转速等参数进行正反向工况的定常模拟，并选取叶轮域的总熵产值参与独立性网格验证。

网格的独立性验证结果如表2所示，其中网格细化因子1与2分别为密中及中疏网格数量的相对值的立方根，数值解1～3分别对应网格由密至疏时的叶轮域总熵产值，当网格数量为984万时，正反向工况下细网格收敛指数分别为0.55%与0.21%，均小于3%，说明方案3（984万网格）的网格精度满足要求。图3为网格划分示意图，总网格数为984万。

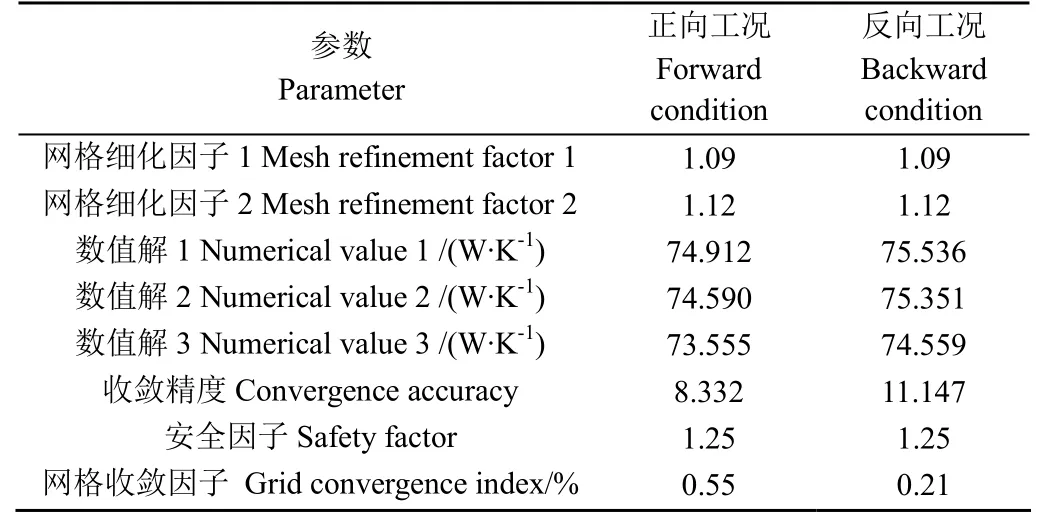
表2 网格独立性验证Table 2 Grid independence verification

2.4 模型验证试验

模型试验是验证数值模拟结果可靠性的重要方式之一，河海大学高精度水力机械多功能试验台如图4所示。进行双向水泵工况试验时，流量从大到小依次测试至少15个工况点，测量点应合理分布在整个能量曲线上，2个工况点之间应保持足够的稳定时间，待试验数据稳定后，测得流量、扬程、转速和轴功率等试验数据。

在正反向不同流量工况下对水泵进行数值模拟，并计算单位流量Q11与单位转速n11。其中，单位流量Q11与单位转速n11公式[9]如下：

3 结果与分析

3.1 模型验证结果

将模拟的外特性曲线与试验值比较（图5a），正向工况下试验值与模拟值的误差小于2%，反向工况下的误差则在3%以内，说明模拟方法准确可靠。与此同时，将熵产计算得到的扬程损失[21]与模型试验的扬程损失进行对比（图5b），正向工况下试验值与模拟值的误差小于2.5%，反向工况下的误差则在3%以内，从而验证了熵产计算的准确性。

3.2 外特性规律

在对水泵进行正反向飞逸工况的模拟之前，先进行30个周期的非定常计算，保留最后5 s的计算结果作为飞逸数值计算的初始场，并将外特性参数进行无量纲处理，如图6所示。正向飞逸工况（FRC）的初始流量为5.86 m3/s，转速为170 r/min，扭矩为7.24 kN·m。反向飞逸工况（BRC）的初始流量为5.08 m3/s，转速为170 r/min，扭矩为7.93 kN·m。

根据机组流量、转速及扭矩的变化情况，水泵在飞逸过渡过程中将经历水泵状态、制动状态、水轮机状态以及飞逸状态（图6）。在飞逸发生之前（0～5 s），机组保持在水泵工况运行，此时外特性参数分别与对应初始值保持一致，正反向飞逸工况的初始扬程均为0.91 m，而正向飞逸工况的初始流量更大且初始扭矩更小，可见该水泵在进入正向飞逸前作泵工况时水力损失更小，这与试验结果相一致，即同一单位流量下正向飞逸工况的扬程损失更小（图5b）；当机组刚断电后（5～10.8 s），叶轮不再对水流提供动力矩，扭矩、转速、流量等参数值持续减小；随后机组进入制动状态（10.8～11.7 s），水流开始倒流，叶轮转速方向保持泵工况旋转方向但转速值逐渐趋向于0；之后机组进入水轮机状态（11.7～27.5 s），叶轮在水流的扭矩作用下开始反向旋转，且转速随流量的增大而增大，此时正反向飞逸工况下转速的差值开始增大；当机组进入稳定飞逸状态时（27.5～42.5 s），外特性参数值基本保持稳定，正向飞逸工况下的流量为10.30 m3/s，转速为271.6 r/min，而反向飞逸工况下的流量为9.32 m3/s，转速为220.5 r/min；可见正向飞逸工况的流量与转速均高于反向飞逸工况，此时2种工况下的扭矩值均在零值附近波动，但正向飞逸工况的扭矩波动的幅值更大。

为了进一步分析叶轮扭矩的波动特性，采用短时傅立叶变换方法（Short-time Fourier Transform，SFFT）对无量纲扭矩值进行处理，窗函数设置为汉宁窗函数，以获取更加准确的脉动频率，如图7所示。由于叶轮扭矩是其正反表面压力绕轴的积分量，说明扭矩的波动将受叶片表面压力脉动的影响，而叶轮室内压力脉动现象与动静干涉相关[24-25]，使得扭矩的波动频率受叶频（Blade Passing Frequency,fBPF）控制。当机组处于水轮机状态或飞逸状态时，正向飞逸工况的脉动频率以叶频及其高次谐波为主，反向飞逸工况的脉动主频为叶频，且正向飞逸工况扭矩波动幅值更高，可见正向飞逸工况下动静干涉作用更强烈。

3.3 熵产演变规律

图8 a所示为总计算域的3项熵产的变化曲线。其中直接耗散熵产占据主导地位，湍流耗散熵产SD′次之，壁面耗散熵产WS最少。根据熵产的计算公式可知，直接耗散熵产与速度梯度密切相关，简化后计算的湍流耗散熵产SD′受湍动能控制，而壁面耗散熵产WS与近壁区水流流速相关。因此机组内流量增大时，流道内的速度梯度、湍动能以及近壁区的流速在宏观上相应增大，使得总计算域3项熵产值与流量的变化规律皆为先减少后增加。对比正反向飞逸工况的熵产值，在断电飞逸前，反向飞逸工况的各项熵产值较大，表明反向泵工况运行时的能量损失较大；在最终飞逸状态下，正向飞逸工况的各项熵产值较大，这可能是因为流态的恶化导致更多的水力能量损失。

水泵在飞逸过渡过程中装置内各过流部件及上下游计算域的总熵产值变化情况分别如图8b与图8c所示。当机组处于稳定飞逸状态时，正反向飞逸工况中熵产最大的过流部件均为叶轮，其次为进水流道。这是因为高速旋转的叶轮内速度梯度的量值较大，同时强烈的动静干涉作用提高了湍动能的量值，且叶轮域具有强壁面效应，因此叶轮域的总熵产值最大；而高速旋流自叶轮室延伸至进水流道，继而使得进水流道的总熵产值仅次于叶轮室。泵装置正反向飞逸过程中，下游计算域由泵工况的稳定来流域转变为飞逸工况的出流区域，出流域受飞逸工况复杂的出水流态影响，因此下游熵产值随飞逸过程的发展逐渐增大；上游计算域同理，由泵工况的出流域转变为飞逸工况的稳定均匀来流域，因此熵产值随时间由大变小。同时飞逸前后对比可见，飞逸工况出水区域相比于泵工况出水区域有着明显更大的熵产值，代表飞逸工况的复杂出流带来了更大的能量损失。

图9 所示分别展示了叶轮、导叶、进水流道、出水流道、下游及上游计算域在飞逸过渡过程中三项熵产值的变化情况。由图9a可知，在机组飞逸后，叶轮域内直接耗散熵产占比最多，壁面耗散熵产SW略高于湍流耗散熵产SD′，可见叶轮域的强壁面效应产生了明显的能量损耗；同时正向飞逸工况下湍流耗散熵产SD′大于反向飞逸工况，这源于正向飞逸工况下更为强烈的动静干涉作用（图7）。由图9b可知，正向飞逸前机组尚处于水泵状态时，导叶位于叶轮的出流方向，而反向飞逸前导叶位于叶轮的入流侧，因此正向飞逸前处于水泵工况下的导叶内复杂的流态致使各项熵产值更大；当机组处于水轮机状态或飞逸状态时，正向飞逸工况下导叶位于叶轮的入流方向，导叶内相对平顺的流态使得各项熵产值较小。由图9c与9d可知，正反向飞逸工况下壁面耗散熵产WS远小于其他2项熵产，即进出水流道中能量损失主要为直接耗散熵产和湍流耗散熵产，近壁区的能量损耗较小。

由图9e与9f可知，正反向飞逸工况下游计算域的湍流耗散熵产SD′占比均高于直接耗散熵产，可见下游计算域流速相对均匀，且水流的湍动效应占据主导；上下游计算域内壁面（计算域底部）耗散熵产WS均近乎为0，占比小于总熵产的0.1%，此时壁面耗散熵产的影响较小。

3.4 全流域流态分布

图10 所示为正反向飞逸工况下全流域子午面处的流线图。在t0时，正反向飞逸工况下进水流道内速度的跨度值分别为4.07与4.22 m/s，正反向飞逸工况下出水流道内速度的跨度值分别为4.47与5.47 m/s，可见反向飞逸工况下进出水流道内速度的跨度值均相应大于正向飞逸工况下的跨度值，这在一定程度上说明反向飞逸工况下的速度梯度较大，这也是反向飞逸工况下直接耗散熵产大于正向飞逸工况的原因（图9c与9d）。在tQ=0时，进出水流道内流态严重失稳，存在强烈的漩涡和回流，但此时流速较低，因而速度梯度与湍动能的量值较小，使得正反向飞逸工况下进出水流道的总熵产值较小（图8b）。在tn=0时，机组已处于倒流状态，此时流道内的流态恶化的程度稍有缓解。在tM=0时，进出水流道内流速近似稳定，同时上游计算域内的流态均已恢复平顺状态，因此上游计算域内熵产值逐渐趋0（图9f）。在t=42.5 s时，机组稳定在飞逸状态，正反向飞逸工况下游域中速度的跨度值分别为2.05 m/s与3.20 m/s，可见反向飞逸工况下速度的跨度值较大，这可能是反向飞逸工况下游域的直接耗散熵产S

D高于正向飞逸工况的原因（图9e）。

3.5 叶轮室涡核分布

图11 所示为tQ=0时正向飞逸工况下涡核与熵产率（EPR）不同圆周截面分布的对比图，并采用特征值Q作为涡识别准则。正向飞逸工况下涡核均聚集于泵工况的叶轮叶片进水边，且靠近轮毂侧叶片展开面处（span=0.05）脱落涡呈聚集态，而临近外壳侧叶轮展开面处（span=0.95）脱落涡呈离散态，可见涡核沿径向呈现逐渐脱离叶片的趋势。与此同时，涡核的出现意味着水流在叶片进水边形成了强度较高的漩涡，较大的速度梯度则产生了较大熵产率，不同截面熵产率与涡核分布较高程度对应相似，这不仅表示涡核聚集之处产生了明显的能量损失，也说明漩涡的产生与演变是熵产率较大和能量损失的重要原因。