谐波磁场下永磁体涡流损耗测试与分析
2021-11-24李永建范子容栗浩森杨占力
耿 惠, 李永建, 范子容, 栗浩森, 杨占力
(1. 省部共建电工装备可靠性与智能化国家重点实验室, 河北工业大学, 天津 300130; 2. 河北省电磁场与电器可靠性重点实验室, 河北工业大学, 天津 300130)
1 引言
稀土永磁电机以其效率高、功率大、结构简单、节能效果显著等优点在工业生产和日常生活中逐步得到广泛应用[1]。近年来,高耐热性、高磁能积钕铁硼永磁体的成功开发,使新型稀土永磁电机的研发取得突破性进展[2,3]。
由于永磁电机采用电力电子变换器驱动,会产生大量的时间谐波,电机分布绕组会在气隙中产生空间谐波,定子开槽引起的气隙磁导变化会在电机气隙中产生齿谐波,这些谐波会在永磁体中引起大量涡流损耗[4-6]。如内转子大功率永磁同步电机工作在额定功率450 kW下,涡流损耗高达2.4 kW,在总电机损耗中的占比可达20%[7]。受永磁电机转子体积和散热的限制,涡流损耗引起的温升会导致永磁体退磁或失磁,降低了电机运行的安全性与可靠性[8,9]。各次谐波在叠加时会对材料磁特性及涡流损耗产生影响,传统的线性叠加得到的损耗值与实际值有一定差别,因此根据实际情况进行必要的材料损耗研究显得尤为重要。
针对谐波激励对永磁体涡流损耗影响的研究,目前大多集中在理论计算及有限元仿真层面。文献[10]介绍了一种利用空间谐波法分析永磁直线发电机的涡流损耗的方法。为了计算涡流,通过在二维笛卡尔坐标系中应用麦克斯韦方程、磁矢量势和法拉第定律来导出解析解。文献[11]以3 kW、1 500 r/min的永磁同步电机为例,建立了二维有限元模型,利用磁热耦合方法分析了电机的电磁场和温度场,得到了损耗和温升数据。根据计算结果,定量分析了电压谐波对永磁同步电机的影响。文献[12]提出了一种基于电磁网络的表面永磁电动机的永磁涡流损耗计算方法,通过所提出的磁阻网络分析模型,计算了包括载波谐波在内的电机永磁体中的涡流损耗。文献[13,14]提出了一种应用叠加原理计算永磁体谐波损耗的方法,即单个谐波分量产生的损耗叠加等于混合后总谐波产生的损耗。上述文献研究大多是从理论计算或者有限元仿真的角度分析谐波磁场对永磁体涡流损耗的影响,部分采用永磁样机进行验证,而鲜有从永磁材料磁特性测量的角度系统分析谐波激励对永磁体涡流损耗影响的研究。
本文从永磁材料磁特性测量[15,16]的角度测量和定量分析了不同谐波激励与永磁体涡流损耗的关系,从谐波次数、谐波含量和谐波相角三个角度研究了谐波对钕铁硼涡流损耗的具体影响。首先,观察和分析了基波叠加不同谐波次数、谐波含量和谐波相角后磁通密度波形的变化。然后,应用永磁体谐波磁特性测试系统测量了不同谐波磁场下钕铁硼永磁体的动态磁滞回线,并分析了磁滞回线的相应变化规律,根据测得的实验数据计算出钕铁硼永磁体的涡流损耗,分别分析了谐波次数、谐波含量和谐波相角对永磁体涡流损耗的具体影响。最后,对比了应用在对温度稳定性要求比较高的仪器仪表类永磁电机中的铝镍钴、应用在对温度可靠性要求比较高的航空航天领域中的钐钴、磁性能最高的钕铁硼三种永磁材料受谐波影响的异同。
2 永磁体谐波磁特性测试系统
永磁体谐波磁特性测试系统包括基于LabVIEW的谐波信号生成和传感信号采集模块、永磁体磁特性测试装置、功率放大器、示波器、水冷电阻和高频阻抗匹配电容箱。其包含的设备型号见表1。

表1 测试系统设备型号
测试系统如图1所示,其中基于LabVIEW驱动的激磁信号生成模块,可实现任意频率、幅值及相位可调的激磁信号的编程,NI 6368数据采集卡进行数模转换,数据采集卡将LabVIEW程序生成的数字信号转变为模拟信号输送给功率放大器。传感信号采集模块,利用NI 6368数据采集卡进行模数转换,数据采集卡将采集到的B-H两个通道的传感信号转换为可供LabVIEW程序分析的数字信号。激磁装置主要是由双C型磁轭、激磁绕组和样品组成,装置中磁轭是由高取向超薄硅钢片叠置而成,可以产生较强的均匀磁场,实现对样品激磁的功能,并使用霍尔探头测试了该激磁装置的气隙磁密,可以看出磁场分布较为均匀,这对于精确测试具有关键作用。选取10 mm×10 mm×10 mm的立方体镀锌钕铁硼样品作为测试对象。为了保证测量精度,H传感线圈紧贴在样品表面,实现样品表面磁场强度的测量。B传感线圈采用线径为0.2 mm的漆包线均匀缠绕在样品表面,实现对样品内部的平均磁密的测量。并利用长直螺线管对线圈系数进行校准,将测得的线圈系数用于反馈控制中B、H信号的采集。功率放大器用于驱动激磁线圈,以保证待测样品在给定频率下可控磁化。匹配电容箱用来消除激磁绕组感抗的影响,使电容和电感串联谐振,整个电路呈阻性,便于激磁。本文采用相位矫正的频域反馈控制技术,控制框图如图2所示。磁通密度设定值与实验值的对比如图3所示。通过设定值与实验值的对比,可以看出所采用的反馈控制方法具有较好的波形控制功能。

图1 永磁体磁特性测试系统

图2 频域反馈控制技术框图

图3 磁通密度设定值与测量值对比
在交变电流激励条件下,永磁材料产生磁滞回线。对于磁性材料的损耗通常是计算整个磁滞回线的面积,它是由样品表面的磁场强度H和样品内的平均磁通密度Bav形成的[17]。公式如下:
(1)
式中,P为总损耗;V为样品的体积;f为激磁频率。测量的总损耗包含涡流损耗和磁滞损耗。对于钕铁硼永磁材料,它的磁导率接近于空气的磁导率μ0,一般在永磁体未失磁情况下认为磁滞损耗几乎可以忽略不计。由于永磁材料较高的电导率,故此永磁材料测试系统测得的结果近似为永磁材料的涡流损耗。
3 谐波激励下钕铁硼的磁特性分析
3.1 谐波激励模型
将磁通密度波形设定为:
(2)
式中,B1为基波幅值;i为谐波次数;αi和θi为各次谐波含量和相角。若αiB1为零,得到的波形即为正弦波;若αiB1不为零,得到的波形即为谐波。通过控制式(2)中的变量i、αi和θi可以得到不同的谐波激励模型,进而对谐波激励对磁特性的影响进行分析。
由Bertotti损耗分离模型[18]可知,正弦磁通作用下总损耗表示为:
(3)
式中,λ为磁通密度指数;kh为磁滞损耗系数;kc为涡流损耗系数;kexc为异常损耗系数。
非正弦多变量条件引入铁损各分量的校正因子[19]后,总损耗可以表示为:
(4)
Fh=1+kΔBT
(5)
(6)
(7)
式中,k为与磁性材料属性相关的系数;Kh、Kc、Kexc分别为修正后的各损耗系数,Kh=khFh,Kc=kcFc,Kexc=kexcFexc;Bm为B波形的幅值;ΔBT为磁通密度反转值;Bn为磁通密度B中n次谐波的幅值。
3.2 谐波次数对钕铁硼动态磁特性的影响
设定基波频率f=1 000 Hz,谐波的含量为50%,相角为0,改变谐波次数i(i=3, 5, 7),激磁模型如式(8)所示,相应的磁通密度的波形如图4所示。

图4 不同谐波次数下的磁通密度曲线
(8)
由图4可以看出,基波叠加各次谐波之后,随着叠加的谐波次数不同,磁通密度的波形在整体趋势不变的情况下出现了局部磁通反转,谐波次数不同,出现的磁通反转的数目也不同。且随着谐波次数的增大,磁通反转的程度也越来越大。
钕铁硼永磁体在基波叠加不同次数谐波时的交流磁场下测得的动态磁滞回线如图5所示。为了更好的效果,将虚线方框的部分进行放大。由图5可以看出,叠加谐波之前与叠加谐波之后磁滞回线形状不同,叠加三次谐波与叠加五次、七次谐波磁滞回线形状也不同。相对于基波对应的磁滞回线,叠加谐波之后磁滞回线上出现了小的磁滞回环,且磁滞回环的数量受叠加谐波次数的影响。在三次谐波条件下,1对小的磁滞回环出现在磁滞回线上,在五次谐波条件下,2对小的磁滞回环出现在磁滞回线上,而在七次谐波条件下,3对小的磁滞回环出现在磁滞回线上。由此可以推断,当基波叠加i次谐波时,磁滞回线上会出现(i-1)/2对小磁滞回环。且随着谐波次数的增大,单个小磁滞回环的面积也越来越大。
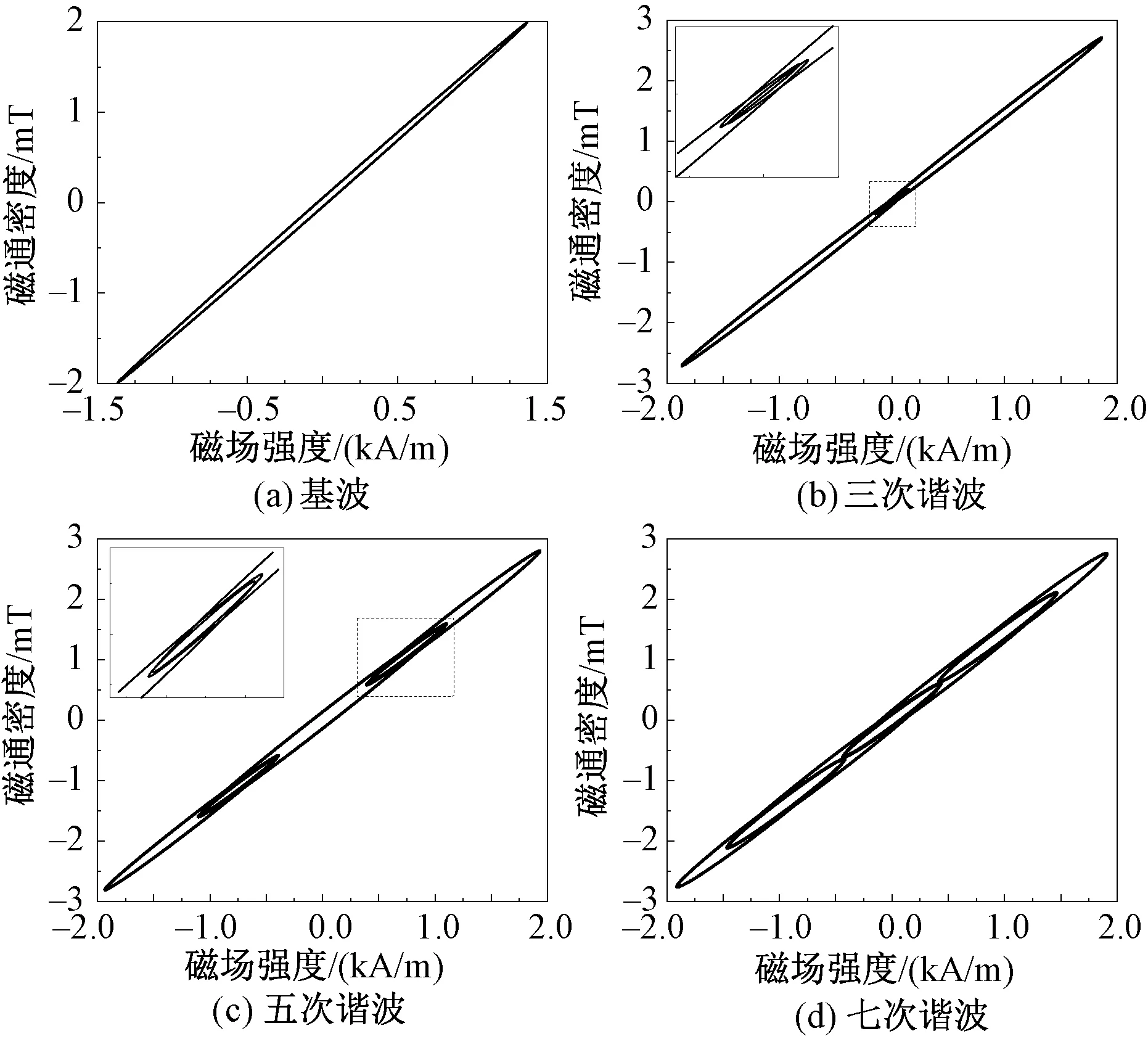
图5 不同谐波次数下的B-H曲线
为了更加直观地分析谐波次数的改变对于永磁体涡流损耗的影响,绘制了不同谐波次数条件下的损耗曲线,如图6所示。

图6 不同谐波次数下的涡流损耗
整体来看,永磁体的动态涡流损耗随基波叠加谐波次数的增加而增加。这是因为随着谐波次数的增加,磁滞回线中小磁滞回环的数量变多,且单个小磁滞回环的面积增大,这两者都导致磁滞回线等效面积变大,式(1)中通过对磁滞回线积分得到的损耗也随之增加。
由式(3)拟合得到的各参数见表2,由表2可以看出,涡流损耗占比最大。

表2 正弦损耗模型拟合参数
根据涡流损耗修正式(4)和式(6),得加入谐波后涡流损耗放大倍数μ为:
(9)
对图6来说,当磁通密度B的大小一定时,在不同次数谐波激励下,钕铁硼的涡流损耗相对于基波激励涡流损耗上升倍数δ计算公式如下:
(10)
式中,Pi为基波叠加第i次谐波激励后的涡流损耗;P1为基波激励下的涡流损耗。
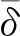
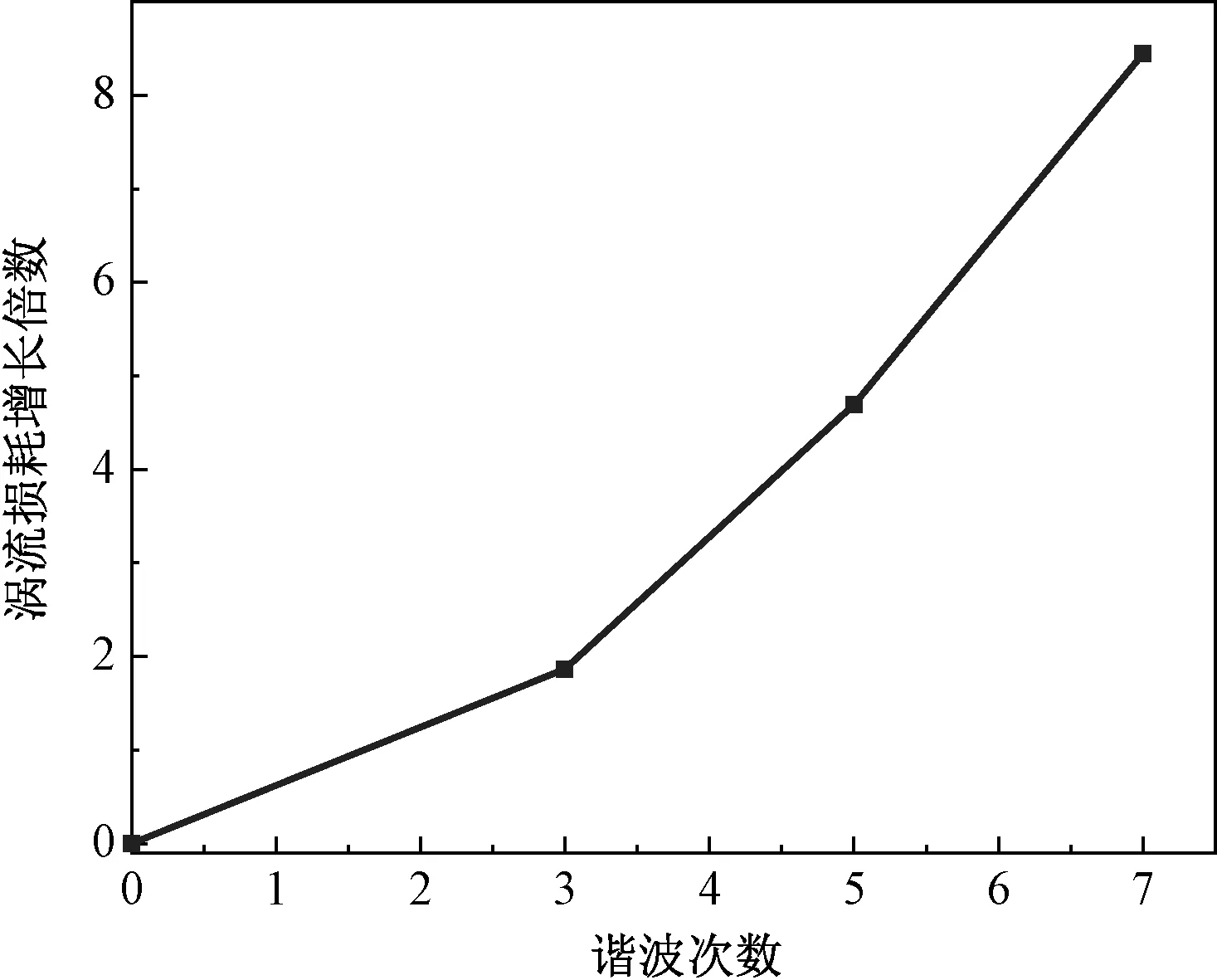
图7 不同谐波次数下的涡流损耗增长倍数
3.3 谐波含量对钕铁硼动态磁特性的影响
设定基波叠加的谐波次数为5次谐波,相角为0不变,改变叠加的谐波含量,激磁模型如式(11)所示,相应的磁通密度B的波形如图8所示。

图8 不同谐波含量下的磁通密度波形
(11)
由图8可以看出,基波叠加不同含量的5次谐波之后,随着叠加的谐波含量的增加,磁通密度B的波形在整体趋势不变的情况下逐渐出现了小的磁通反转,且谐波含量越大,磁通密度B的波形反转的程度也越大。因为谐波次数相同,所以波形中磁通反转的数目也相同。
钕铁硼永磁体在基波叠加不同含量5次谐波时的交流磁场下测得的动态磁滞回线如图9所示。为了观看的效果,将虚线方框的部分进行放大。由图9可以看出,相对于基波对应的磁滞回线,叠加不同含量的5次谐波之后磁滞回线上逐渐开始出现固定数量的小磁滞回环,且小磁滞回环的面积随着基波叠加的谐波含量的增加而增加。但当基波叠加10%含量的5次谐波时,磁滞回线两端出现了向内靠拢的趋势,并没有出现小磁滞回环,这是因为图8(b)所示的磁通密度B的波形并没有出现磁通反转。但是随着5次谐波含量的增加,30%含量的谐波使磁滞回线上出现了小磁滞回环,50%含量的谐波使磁滞回线上出现的小磁滞回环更大,这是由如图8所示的叠加更多含量5次谐波之后磁通密度B的波形开始反转而且反转程度越来越大导致的。

图9 不同谐波含量下的B-H曲线
如图10所示,绘制了基波叠加不同5次谐波含量条件下的损耗曲线。从图10可以看出,永磁体的涡流损耗随基波叠加谐波含量的增加而增加。这是因为随着谐波含量的增加,永磁体磁滞回线波形中逐渐出现小磁滞回环并且小磁滞回环越来越大,这些小磁滞回环使磁滞回线的等效面积变大导致了更多的损耗。
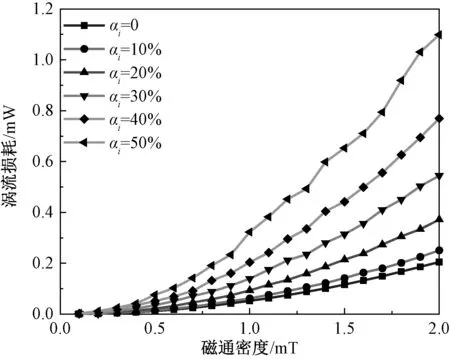
图10 不同谐波含量下的涡流损耗
当磁通密度的大小B取值一定时,钕铁硼在不同谐波含量激励下的涡流损耗相对于基波激励涡流损耗上升倍数ε计算公式如下:
(12)
式中,Pαi为基波叠加不同含量谐波激励后的总损耗;P1为基波激励下的涡流损耗。


图11 不同谐波含量下的涡流损耗增长倍数
3.4 谐波相角对钕铁硼动态磁特性的影响
设定谐波次数为5次谐波和含量为50%不变,改变谐波相角θi(θi=30°,60°,90°,120°,150°,180°),相应的磁通密度B的波形如图12所示。由图12可以看出,基波叠加不同相角的谐波之后,随着叠加的谐波相角的不同,磁通密度B的波形在整体趋势不变的情况下出现了不同位置的磁通反转。在相角逐渐增大的过程中,磁通反转的位置沿着横坐标逐渐左移,即谐波的相角最终影响的是磁通反转的位置,但磁通反转的程度和数量不变。

图12 不同谐波相角下的磁通密度曲线
钕铁硼永磁体在基波叠加不同相角谐波的交流磁场下测得的动态磁滞回线如图13所示。由图13可以看出,相对于基波对应的磁滞回线,叠加不同相角谐波之后磁滞回线上出现小的磁滞回环的位置不同。这是因为随着谐波相角的增加,磁通密度曲线B上磁通反转的位置不同,导致相应的磁滞回线上出现的小磁滞回环的位置不同。随着相角的增大,每对小磁滞回环中都有一个逐渐往曲线的中间聚拢,另外一个逐渐移动到闭合曲线的顶角处。但移动过程中小磁滞回环的大小不变,因为图12中磁通反转的程度不变。

图13 不同谐波相角下的B-H曲线
为了更加直观地分析谐波相角改变对于涡流损耗的影响,绘制了不同谐波相角条件下损耗曲线,如图14所示。整体来看永磁体的涡流损耗并不随基波叠加谐波相角的变化而变化。这是因为谐波相角的增加只是改变了小磁滞回环出现在磁滞回线上的位置,并没有改变单个小磁滞回环的面积以及小磁滞回环的数量。由于此时永磁体的磁化为线性磁化,因而小磁滞回环位置的改变并不会影响小磁滞回环的面积,所以总涡流损耗并不改变。与式(9)计算得出的损耗不变具有较好的一致性。
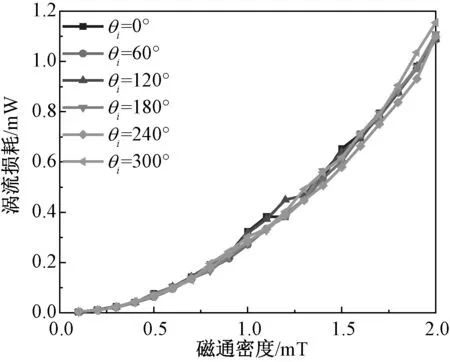
图14 不同谐波相角下的涡流损耗
3.5 多个谐波分量叠加对钕铁硼磁特性的影响
设定叠加的谐波为:3次谐波,含量50%,相角为0;5次谐波,含量30%,相角为0;7次谐波,含量20%,相角为0。磁通密度B的波形如图15(a)所示,B-H曲线如图15(b)所示,涡流损耗曲线如图15(c)所示。由图15(a)可以看出,叠加之后B波形共存在3对磁通反转;相应的图15(b)B-H曲线共存在3对局部磁滞回环;图15(c)中叠加完三种谐波后,涡流损耗明显增大,计算出相对于基波,涡流损耗增加了7.18倍,与式(9)计算得出的倍数6.4相差不大。

图15 多次谐波叠加下的磁特性
4 谐波激励下不同永磁材料磁特性对比
4.1 谐波对钕铁硼、钐钴、铝镍钴磁特性的影响
设定谐波次数为5次谐波和含量为50%不变,谐波相角θi为0,对谐波对铝镍钴、钐钴磁滞回线的影响进行了测量及对比分析,如图16所示。由图16可知,铝镍钴出现了明显的小磁滞回环,钐钴磁滞回环小于铝镍钴,钕铁硼最小。在相同的磁通密度幅值下,铝镍钴需要的激磁磁场强度值H最小,因为铝镍钴的相对磁导率高于钕铁硼和钐钴。

图16 谐波激励下不同永磁材料的B-H曲线
4.2 谐波对钕铁硼、钐钴、铝镍钴涡流损耗的影响
如图17所示,绘制了相角θi为0°时不同材料随谐波次数和含量变化的涡流损耗。其中,最上层为铝镍钴涡流损耗,中间层为钐钴涡流损耗,最下层为钕铁硼涡流损耗。铝镍钴永磁体的涡流损耗要稍大于钐钴,钐钴大于钕铁硼。这是因为铝镍钴的小磁滞回环最大,而钐钴从磁滞回环来看,比铝镍钴要小很多,但最终损耗曲线并没有小很多,这是因为铝镍钴的磁导率高于钐钴,从而达到相同的磁通密度需要的激磁磁场较小,所以磁滞回线的面积并没有比钐钴大很多。但钐钴与钕铁硼的磁导率相近,所以在钕铁硼小磁滞回环比钐钴小的情况下,涡流损耗也比钐钴小很多。
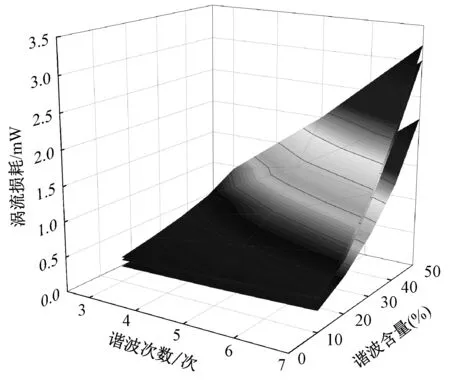
图17 谐波激励下不同永磁材料的涡流损耗
5 结论
本文针对谐波对永磁体涡流损耗的影响进行了测量分析,测量了钕铁硼永磁材料在不同谐波激励下的交变磁特性,从谐波次数、谐波含量、谐波相角三个因素说明了谐波激励对永磁体涡流损耗的影响。可以得出以下结论:
(1) 基波叠加谐波次数的不同,主要影响磁通密度B的波形上磁通反转的数目和程度。谐波次数越大,磁通反转的次数越多,反转的程度越大,进而增大了磁滞回线等效面积,最终增大了永磁体涡流损耗的大小。
(2) 基波叠加谐波含量的不同,主要影响磁通密度B的波形上磁通反转的程度。谐波含量达到一定程度会造成磁通反转,磁通反转的程度随着谐波含量的增加而增加,磁滞回线上小磁滞回环的大小也随之增加,最终导致永磁体涡流损耗的上升。
(3) 基波叠加谐波相角的不同,主要影响磁通密度B的波形上磁通反转的位置,但不改变反转的程度。即谐波相角只影响磁滞回线上小磁滞回环出现的位置,而不影响小磁滞回环的大小和数目,因此也不影响永磁体涡流损耗的大小。
(4) 铝镍钴磁滞回环大于钐钴,钐钴磁滞回环大于钕铁硼,但最终铝镍钴涡流损耗仅稍大于钐钴,同时明显大于钕铁硼。
研究结果对永磁电机电磁设计及材料选用阶段具有重要的参考价值,它还可以提供有效的分析方法和必要的数据支持。
