考虑脉冲负载影响的直流微电网变换器模型预测控制策略

2021-11-24赵新宽陈燕东姜洪朝

电工电能新技术 2021年11期

赵新宽，陈燕东，姚鹏，姜洪朝

(1. 珠海城市职业技术学院珠海市智能电网技术协同创新中心，广东珠海 519000； 2. 湖南大学国家电能变换与控制工程技术研究中心，湖南长沙 410082； 3. 珠海万力达电气自动化有限公司，广东珠海 519000； 4. 中国电子信息产业集团有限公司第六研究所，北京 102209)

1 引言

随着电力电子技术的发展，直流微电网相关技术将成为未来新能源接入、全电飞机或船舶的核心关键架构。直流微电网能提供高效且可靠的配电，并通过简单控制对能量进行灵活管理[1-3]。对于全电船舶而言，负载类型较为多样，包含常规负载、推进负载、脉冲负载(Pulsed Power Load，PPL)和专用高功率负载等[4,5]。其中PPL会间歇性从电网中消耗大量功率，具有一种高功率脉冲行为特性，可能导致电网电压波动和跳变，甚至导致整个直流微电网失电[6,7]，故对系统运行和控制提出了很高的要求。对此，直流微电网中设置基于电池组或超级电容的储能系统(Energy Storage System，ESS)可对PPL进行关键条件下的补偿，从而提高系统可靠性和效率[8-10]。

通常增加电池组储能的主要方法是增加电池数量，故功率成本折中和电流均分问题使得其不是最理想补偿PPL的方案。而超级电容由于其内阻低、功率密度高和循环寿命长，是一种对电池组较好的储能补充，可形成混合ESS方案[11-13]。混合ESS方案下，PPL暂停时，超级电容平滑充电，而在PPL工作时，其快速放电进行功率缓冲。文献[14]指出混合ESS可减少内部损耗，并增加ESS的寿命，故较单电池组具有更好的性能。混合ESS若直接接入直流侧，则称为无源混合ESS，其优点是成本低和损耗小。但电池组和超级电容直接并联连接会限制两者之间的功率均分，故可设置变换器接入到直流侧，则该配置称为有源混合ESS。文献[15]中指出有源混合ESS可通过变换器调节功率流，故可使得ESS体积容量更小。由于有源混合ESS经由变换器接入直流侧，故需分析系统稳定性和进行协调控制策略设计[16-18]。同时，构建的控制方案必须能考虑PPL、ESS和系统之间的交互来减轻PPL的不利影响[19]。文献[20]提出了混合直流储能的瞬时功率控制方案，并在直流母线上配备了电压滞环保护。文献[21]中提出基于极限电压的控制结构，可根据变换器功率和电源可用功率的限制，控制直流电压尽可能快地为ESS充电。文献[22，23]设计了一种平均电流控制方案，其试图将变换器输出电流尽量保持恒定以减轻对变换器和ESS的影响。文献[24，25]中利用自适应补偿器和滑动平均测量技术设计了电流-电压协调控制方案，可实现对变流器电流和直流电压的同时控制。但上述方案均没有考虑ESS电压限制问题，也忽略了系统硬约束。

目前，随数字芯片发展，模型预测控制(Model Predictive Control，MPC)在电力电子变换器中的应用前景趋于广阔[26,27]。MPC可通过最优化成本函数计算直接获取变换器控制信号来实现最优控制。故本文将MPC引入到直流微电网变换器控制中，实现了一种简单、鲁棒性好且高效的直流微电网控制策略。不同于传统控制方法，所设计的控制系统不仅考虑了系统硬约束，还具备将直流微电网输出电压和电流保持在工作点附近较小区域中的能力，同时还保证了超级电容快速充电，以应对PPL的不利影响。最后，通过实验验证了所设计MPC方案的效果。

2 直流微电网配置及其动态建模

本文研究对象为全电船舶直流微电网[28]，如图1所示，包含发电机组、混合ESS、PPL、推进负载和常规负载等。其中混合ESS用于补偿直流侧的电压波动。此外，还有能量管理控制系统参与进行分散式或集中式的系统能量调度和控制，实现在一些预定目标下优化系统运行。直流微电网中还配备有系统保护，由变换器控制和直流断路器组合实现，以应对系统故障。

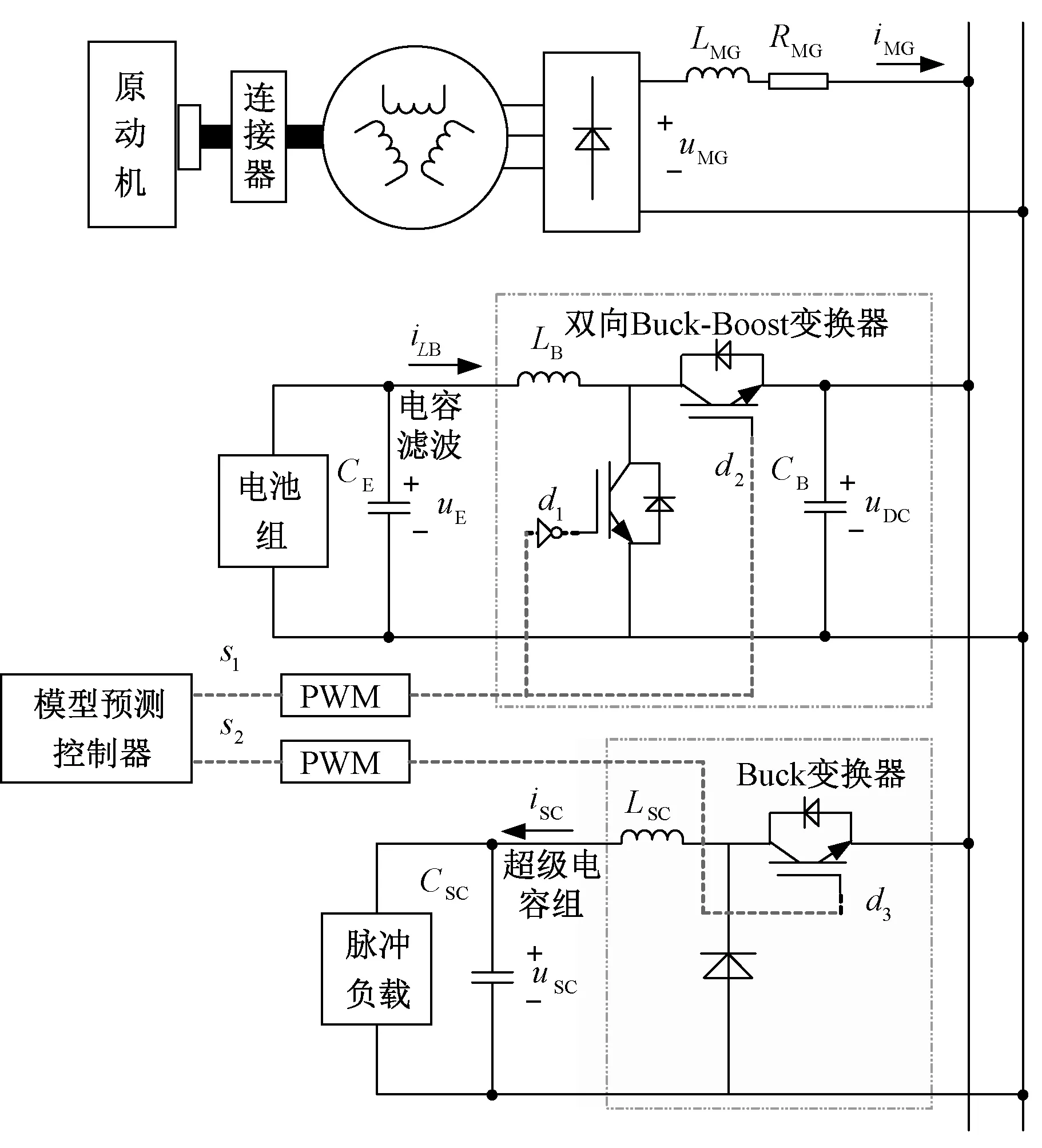
图1 直流微电网配置

2.1 直流微电网配置

图1中直流微电网的电源由三相同步发电机组及不控整流器组成，整流器输出电压为uMG。混合ESS包含超级电容和电池组，分别经Buck变换器和双向Buck-Boost变换器接到直流侧[29]。在孤岛模式或高负载等工况下，电池组可为直流电压提供长期支持；而在正常情况下电池组将进行充电。此外，PPL通过功率缓冲器连接到直流母线，功率缓冲器即由超级电容组成，超级电容通过直流侧充电后断开连接，当PPL激活时，其迅速放电以达到功率缓冲的目的。

2.2 ESS动态模型

图2(a)为锂离子电池组的经典电路模型[30]。图2(a)中，Rp和Cp分别是极化电阻和电容。电池组的充电状态可定义为：

(1)

式中，SOC为电池组荷电状态；CESS为电池组标称容量；ib为负载电流；kt为充电系数。对式(1)进行微分运算可得：

(2)

式中，Rb为电池组内阻；uE为输出电压；up为极化电容电压；uoc是电池组内电压。将图2(a)中电路模型结合双向Buck-Boost变换器电路可得图2(b)中的电池组接入直流侧电路模型。结合图1，可推导得到混合ESS的状态空间模型为：

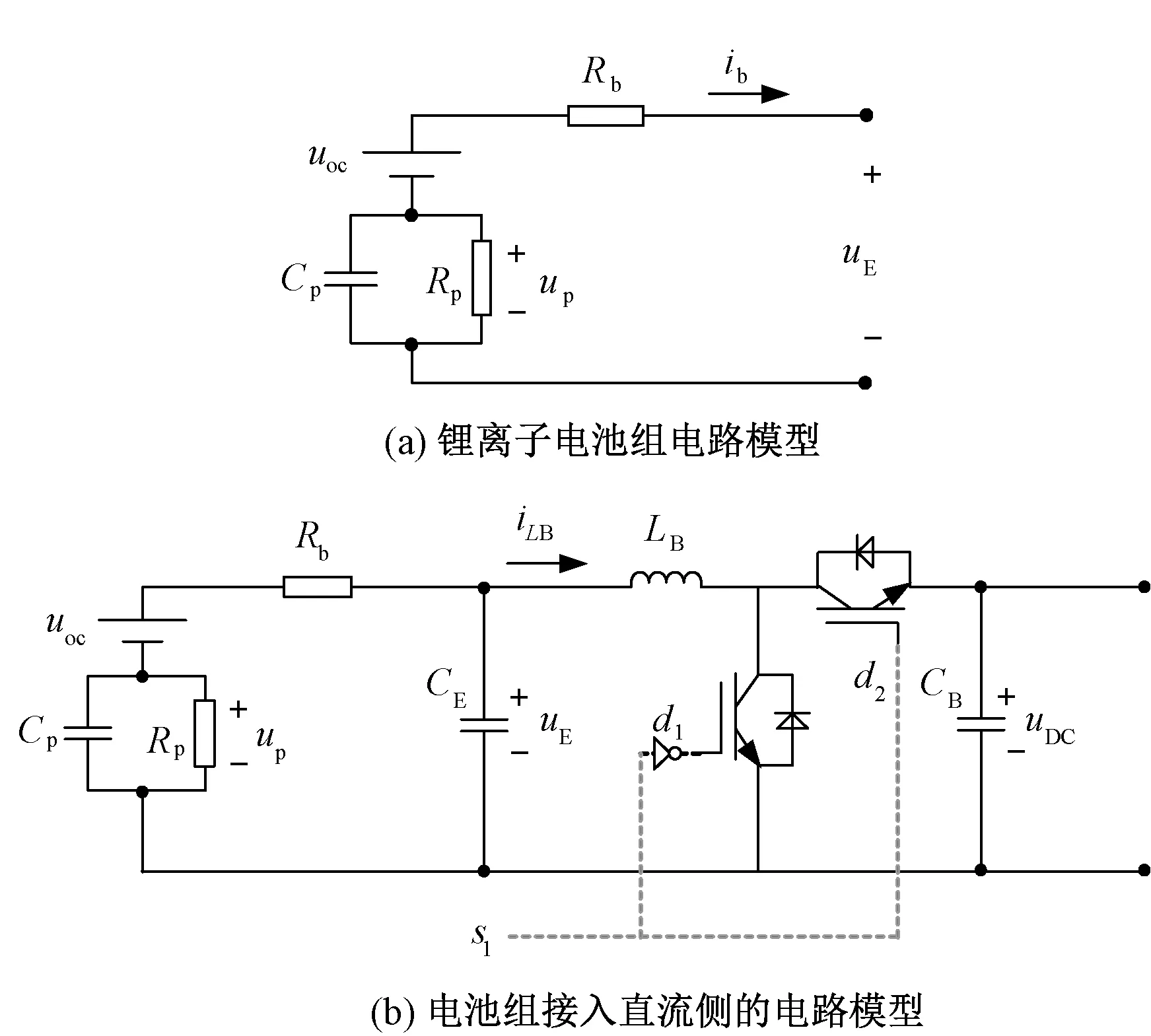
图2 ESS电路模型

(3)

式中，s1和s2分别为双向Buck-Boost变换器和Buck变换器的控制信号；LB和CE分别为双向Buck-Boost变换器电池侧电感和电容；CB为双向Buck-Boost变换器直流母线侧电容；RLB为LB的寄生电阻；iLB为流过LB的电流；uDC为直流母线电压；iSC为Buck变换器内电感LSC上电流；iMG为直流源输出电流。

2.3 PPL动态模型

图3所示为ESS及其功率缓冲器的电路模型。考虑到PPL突然需要较高的功率，因此设置了超级电容由Buck变换器接入到直流侧进行缓冲。根据图3，可推导得PPL的状态空间模型为：

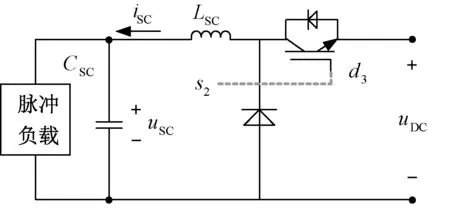
图3 PPL电路模型

(4)

式中，CSC为超级电容的容值；uSC为CSC上的电压；LSC为Buck电路内电感；RSC为LSC的寄生电阻；PPL(t)为脉冲负载功率。

2.4 直流源动态模型

如图4所示为直流源电路模型，据此可推导得到直流源的状态空间模型为：

图4 直流源电路模型

(5)

式中，RMG和LMG分别为对直流侧电压的压降进行模拟而设置的电源内阻和内电感；uMG和iMG分别为直流源输出电压和电流。

2.5 直流微电网的动态模型

根据前述对直流微电网中各组成部分的建模及其状态空间模型推导，可构建出整个直流微电网的状态空间模型。设z=[z1z2z3z4z5z6z7z8]T=[uEupuDCiLBuSCiSCiMGSOC]T，而脉冲负载功率PPL(t)为未知扰动d(t)，联立式(3)～式(5)可得直流微电网的状态空间模型为：

(6)

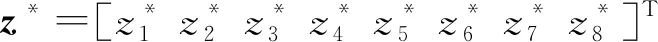
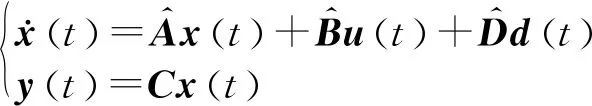
(7)

其中

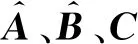
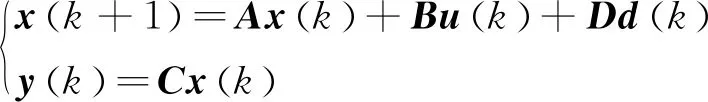
(8)

式中，A、B、C和D为离散模型中的常系数矩阵；k为步长。

3 系统约束分析

图1中所示直流微电网配置可在极端工况条件下，使系统运行能力最大化。根据1～35 kV中压直流电网标准[28]，在设计控制策略时需考虑系统约束，以保证输出电能质量。图1中直流微电网各个设备均由电力电子变换器连接到直流侧，因此需进行协调控制。此外，通过使用主动配置可以限制故障电流。根据图1中系统配置，可以提取出主要的系统约束如下：①发电机组是通过不控整流器实现交流电能向直流侧的输送，输出电流为iMG，其中不控整流器中必须使用半导体限流装置；②需确保直流母线电压uDC在允许范围内；③由于直流变换器存在电流限制，即iLB和iSC存在最大限制，故过电流保护是必要的；④超级电容电压uSC需控制为较高且相对稳定，以补偿PPL高脉冲功率的影响；⑤变换器由PWM调制器生成的0/1脉冲信号进行控制。下面设计MPC方案时将考虑上述所有列出的系统约束。

4 直流微电网变换器MPC方案设计

MPC广泛用于各类工业场景中，可很好地解决带约束的控制问题。MPC方法较传统控制技术具有优势如下：①可处理多输入多输出系统；②可对输入输出信号严格限幅；③MPC方法可用于包括延迟、不确定性或扰动的非线性系统。

MPC方案设计的关键在于求解约束下的最优化问题，这需要基于系统模型计算状态变量和控制信号在预测范围内的演变，并在每个步长得到使预测结果最优的控制信号施加到系统中。由于MPC中最优问题的结构可以转换为凸结构，因此可以使用线性矩阵不等式方法进行数值求解。

对于式(8)所描述的离散时间域系统，由于没有确切的扰动值，故在MPC设计过程中不考虑扰动。基于式(8)，可计算输出变量的N步长预测值为：

(9)

从式(9)可构建输出预测矩阵Y(k)为：

Y(k)=Fx(k)+GU(k)

(10)

其中

为了评估不同控制输入作用下系统的性能，需定义与性能指标相关的成本函数表达式。当成本函数最小化时，则意味着系统在所期望的条件下运行。MPC中成本函数设计为：

(11)

式中，P和Q为已知的正定加权矩阵；w(k)为输出参考值。利用下面的不等式，可使式(11)所描述的成本函数最小化：

[Y(k)-w(k)]TP[Y(k)-w(k)]+

UT(k)QU(k)<γ

(12)

式中，性能指标γ是正定函数，必须通过优化问题将其最小化[31]。由于式(12)中所包含的成本函数是非凸的，故需要将式(12)转为凸结构。下面引出引理1。下文中，对于一个对称矩阵M，采用“M>0”、“M<0”、“M≥0”和“M≤0”分别表示M为正定、负定、正半定和负半定。此外，diag{}代表对角矩阵。

引理1[32]：考虑一个仿射函数F′，其划分为：

(13)

当且仅当满足以下不等式之一时，有F′<0。

(14)

定理1：如果存在决策矩阵变量K(k)满足以下具有线性矩阵不等式约束的凸优化问题，则将使成本函数式(12)最小化。

γ最小化，则有：

(15)

所获得的控制信号不仅试图将输出变量保持在恒定值，并同时使性能指标γ最小。此外，还保证了输出和控制信号的幅值在预设置区域内，该预设置区域由Umax、Umin、Ymax和Ymin定义。

证明：将式(10)代入式(12)，可得：

(16)

式(16)可重写为如下形式：

(17)

通过使用引理1，将双线性矩阵不等式(16)转换为线性矩阵不等式条件，如下所示：

(18)

其中H11(k)为：

(19)

另外，对输出信号和控制信号幅值的约束如下：

(20)

式中，Y(k)=Fx(k)+GU(k)。由于以上约束式是非凸的，为了将非凸条件转换为凸条件，以对角矩阵的形式重新表示式(20)，从而式(20)转换为线性矩阵不等式。至此，证明完成。

5 实验验证

为验证所设计的直流微电网变换器MPC方案的性能，采用和文献[24]中所描述传统控制方案进行了对比测试，其中实验平台如图5所示。图5中直流微电网实验平台设有单个PPL，功率为2 kW，工作频率为0.2 Hz，占空比为20%，即功率谱设置如图6所示。

图5 实验平台

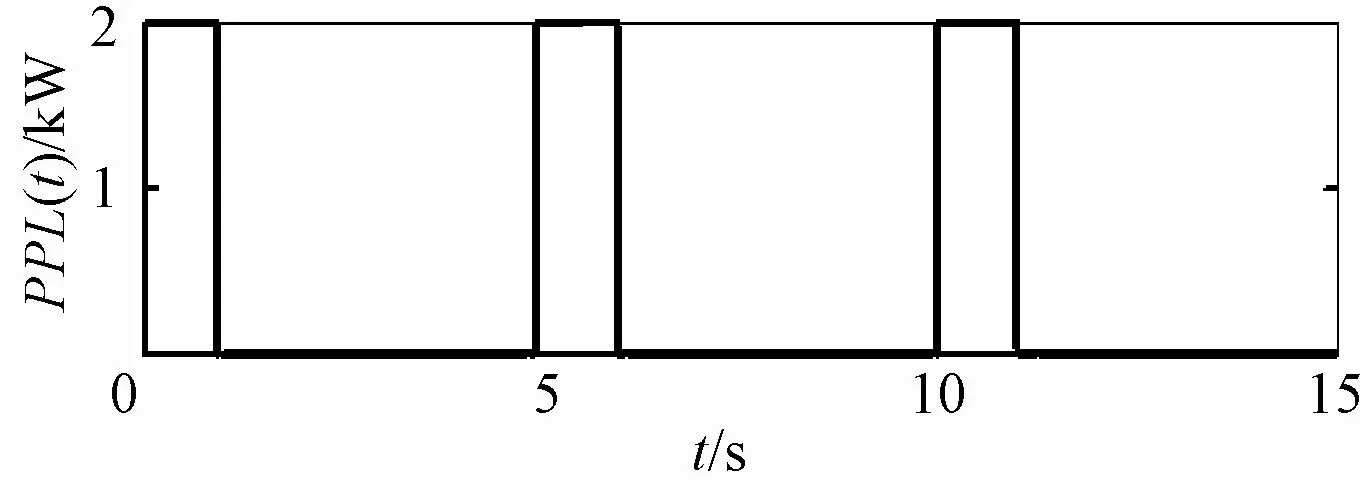
图6 PPL功率谱设置

系统其他主要参数设置为：直流源动态模型中内电阻RMG和电感LMG分别为0.1 Ω和3 mH；超级电容CSC为0.1 F，其对应的Buck变换器中电感LSC为3 mH；电池组侧双向Buck-Boost变换器中电感LB和电容CB分别为3 mH和680 μF。除了系统参数外，工作点和输出参考值设置为：

同时输出信号设置的边界为：

MPC算法中预测步长设置为N=4，采样周期设置为T=1 ms。此外，在考虑状态变量需满足无量纲条件，以及不同输出变量的权重后，设置成本函数式(12)中的加权矩阵P和Q如下：

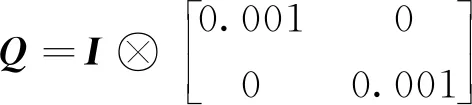
式中，“⊗”为Kronecker积；I为单位矩阵。通过应用定理1中的最优算法，可以计算每个采样周期的状态反馈控制增益矩阵。优化求解是基于Matlab平台中的YALMIP工具箱实现的。进一步，基于Matlab/Simulink平台构建控制律，并在dSPACE(DS1202)系统上生成可执行实时运行代码，进而生成控制信号施加到Semikron变换器组件中。

如图7所示为采用所设计的MPC方案下的直流微电网运行结果，同时还包含了传统控制方案时的测试结果，以方便进行对比。其中直流微电网中的直流母线电压uDC的波形如图7(a)所示，从实验结果中可以看出，传统控制方案下，直流母线电压较参考值相差更大，而MPC可有效补偿PPL带来的不利影响，使实际母线电压较好地跟踪参考值。图7(b)为双向Buck-Boost变换器电流iLB的波形，图7(c)为超级电容CSC上电压uSC的波形，超级电容分别在PPL工作和不工作期间放电和充电，相对于传统控制方案，MPC方案下超级电容可尽快充电，故参考值跟踪性能更好，这也可从图7(d)为超级电容CSC充电电流iSC的波形看出，电流响应更快。图7(e)为直流源输出电流iMG的波形，可看出，传统方案下，直流源须注入大电流以补偿响应慢的问题，这意味着整流器上的电流过高，将提高整流器功率开关器件的电流应力要求。而所提出的MPC方案可保持整流器输出电流在预定范围内，对系统设计更为有利。

图7 对比实验结果

从图7的实验结果可观察出，传统控制方案和新型MPC方案都可以补偿PPL的影响。新方案的优势体现在系统瞬态响应明显更快，可使超级电容尽快充电，并在稳态下，输出变量快速收敛到所定义的参考值。而传统方案下参考跟踪的偏差较大，如表1所示为误差信号的两种范数在两种控制方案下的对比关系，更清楚地反映出所提出的MPC方法相对于传统控制方法的显著改进。此外，MPC控制器可直接实现对直流微电网中Buck变换器和双向Buck-Boost变换器的最优鲁棒协调控制，而传统方案则是对两者分别进行控制的。