避免轨迹方程增解和漏解的策略

廖永福

(福建省厦门第二中学 361009)

避免轨迹方程产生增解和漏解的对策主要有：全面考查所有可能出现的情况；充分挖掘题中隐含的数量关系；注意化简、消参前后方程是否同解；仔细检验特殊点是否符合题意.下面以近年高考题为例.

一、全面考查所有可能出现的情况

在求轨迹方程时，有时由于某些参数的不确定性，或者图形形状、位置关系的不确定性，需要对其进行分类讨论，全面考查所有可能出现的情况.如果分类重复或遗漏，就有可能产生增解或漏解.

A.圆 B.椭圆 C.双曲线 D.抛物线

分析建立平面直角坐标系，设出点M,A,B的坐标，通过已知条件求出点M的轨迹方程，再作出判断.

解析以AB所在的直线为x轴，AB的中垂线为y轴，建立平面直角坐标系，设M(x,y)，A(-a,0)，B(a,0)(a>0).

当λ=1时，方程表示圆；当λ>0且λ≠1时，方程表示椭圆；当λ<0时，方程表示双曲线；当λ=0时，方程表示直线.

综上，方程不表示抛物线.故选D.

点评本题考查曲线轨迹方程的求法，轨迹方程与轨迹的对应关系，考查分类讨论思想、分析问题、解决问题的能力以及计算能力，属于基础题.这里要对常数λ进行分类讨论，如有遗漏，就会导致解答错误.

例2(2016年全国Ⅲ卷)已知抛物线C:y2=2x的焦点为F，平行于x轴的两条直线l1，l2分别交C于A，B两点，交C的准线于P，Q两点.若ΔPQF的面积是ΔABF的面积的两倍，求AB中点的轨迹方程.

分析利用△PQF和△ABF面积之间的关系，求出点N的坐标，再利用点差法求AB中点的轨迹方程.

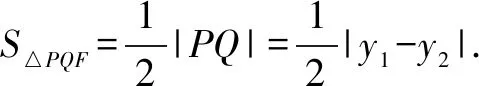
因为S△PQF=2S△ABF，所以2|FN|=1.解得xN=1.

即N(1,0).

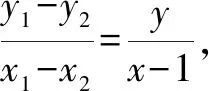
当直线AB的斜率不存在时，AB⊥x轴，点M与N重合，即M(1,0)，它满足y2=x-1.

综上，AB中点的轨迹方程为y2=x-1.

点评本题考查抛物线的方程与性质，考查轨迹方程的求法，解题关键是根据AB与MN斜率相等列出方程，属于中档题.这里要注意对AB的斜率是否存在进行讨论，如果忽视AB斜率不存在的情况，就有可能丢失符合条件的点M(1,0)，造成漏解.

二、充分挖掘题中隐含的数量关系

隐含条件是指题目中含而不露、不易察觉的条件.在解答轨迹问题时，忽视隐含条件将导致思路中断或解题错误，因此，解题时要认真读题，仔细分析，及时发现和利用题目中隐含的数量关系，提高解题的有效性和准确性.

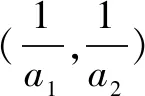
A.直线 B.圆 C.椭圆 D.双曲线

由lny1+lny2=0，得y1y2=1，即(1-2a1)(1-2a2)=1，化简，得2a1a2=a1+a2.

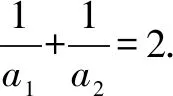
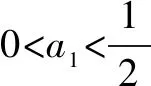
所以x+y=2(x<0或x>2)，故所求的轨迹是两条射线(不含端点).

点评本题考查轨迹的求法，考查圆的定义和性质，属于中档题.解题时，不仅要用足已知条件，还要充分挖掘题中隐含的条件，如1-2a1>0和a1≠0等，命题者忽略了这些隐含条件，致使本题设计不严谨.

三、注意化简、消参前后方程是否同解

在化简方程时，要注意化简前后未知数的取值范围是否一致，确保化简过程是同解变形；在把参数方程化为普通方程时，要注意参数的取值范围对动点横、纵坐标的制约作用，确保消参前后方程是等价变形.否则，就有可能产生增解或漏解.

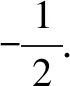
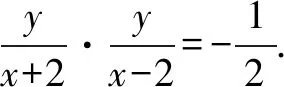
①

②

由x+2≠0且x-2≠0，得x≠-2且x≠2，即y≠0.

点评本题考查用直接法求轨迹方程，属于基础题.解题时，如果不注意方程①中x的限制条件x+2≠0且x-2≠0，就会导致方程①和②不同解，曲线C的方程就会产生增解，M的轨迹就会混进不符合条件的点.

分析设直线l的方程为x=ty+1(t∈R)，代入椭圆方程，消去x，得(t2+2)y2+2ty-1=0，利用韦达定理求出△F1AB的重心坐标，进而求出重心的轨迹方程.

解析F1(-1,0)，F2(1,0).因为F1∉l，所以可设直线l的方程为x=ty+1(t∈R).

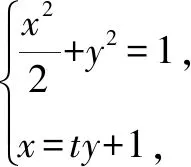
故△=4t2+4(t2+2)>0恒成立.

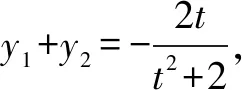
消去t，得9x2+18y2=1.

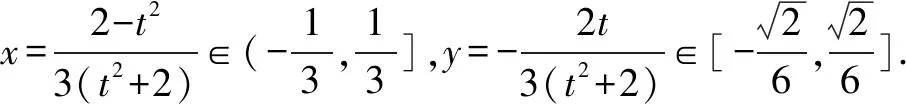
点评本题考查三角形重心的轨迹方程的求法，考查椭圆、直线方程、三角形重心坐标公式等基础知识，考查运算求解能力，考查函数与方程思想，属于中档题.消参时，如果不注意参数t的取值范围对x,y的约束作用，就有可能产生增解，导致解题失误.

四、仔细检验特殊点是否符合题意

求轨迹方程时，既要考虑动点运动的一般情况，又要考虑动点运动的特殊情况，如动点在极限位置、临界位置等特殊位置时是否符合题意，忽视对这些特殊点的检验，也有可能产生增解或漏解.

例6 (2016年全国Ⅰ卷)设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1,0)且与x轴不重合，l交圆A于C，D两点，过点B作AC的平行线交AD于点E.证明|EA|+|EB|为定值，并写出点E的轨迹方程.

分析求出圆A的圆心和半径，运用直线平行的性质和等腰三角形的性质，可得EB=ED，再由圆的定义和椭圆的定义，可得E的轨迹为以A，B为焦点的椭圆，求得a，b，c，即可得到所求轨迹方程.

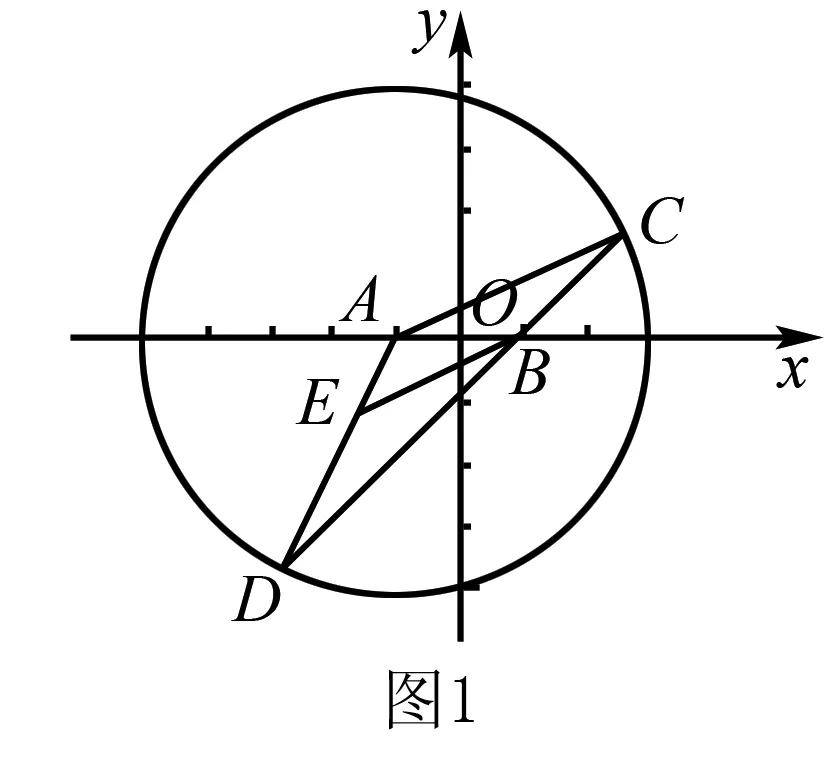
解析如图2，圆A的标准方程为(x+1)2+y2=16，可得圆心A(-1,0)，半径r=4.

由BE∥AC，得∠C=∠EBD，由|AC|=|AD|，得∠C=∠D.

所以∠D=∠EBD.所以|EB|=|ED|.则|EA|+|EB|=|EA|+|ED|=|AD|=4>|AB|.

所以点E在以A，B为焦点的椭圆上.

又直线l过点B(1,0)且与x轴不重合，所以点E不在x轴上.

点评本题考查轨迹方程的求法，注意运用椭圆和圆的定义，属于基础题.解题时，如果忽视对隐含条件“直线l过点B(1,0)且与x轴不重合”的挖掘，忽略对椭圆长轴两个端点的检验，就会产生增解，导致解题错误.

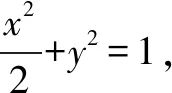
A.椭圆 B.双曲线 C.圆 D.抛物线

分析本题可以用参数法求出动点P的轨迹方程，也可以通过考查特殊点作出判断.

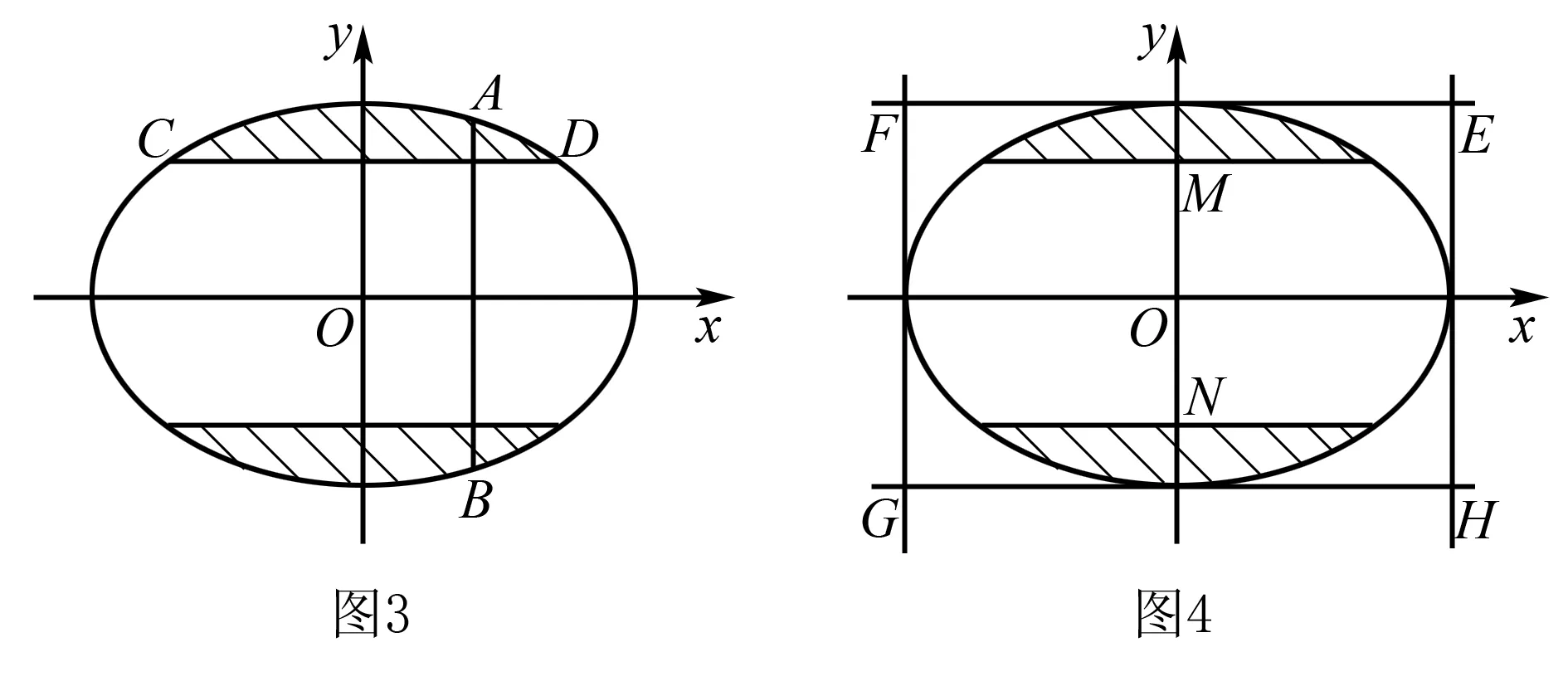
实际上，由于0<|AB|=|CD|≤2，当|AB|=|CD|=2时，两直线交点为M，N，当|AB|=|CD|趋近于0时，两直线交点趋近于E，F，G，H，如图4，对照题目中的四个选项，可以断定点P的轨迹是双曲线落在矩形EFGH内部的两段曲线(不含点E，F，G，H).

点评本题考查轨迹方程的求法与判断，属于中档题.通过考查特殊点，避免了轨迹方程增解的产生，快速准确地得到问题的答案.

可见，在解答轨迹问题时，不仅要熟练掌握求轨迹的常用方法，如直接法、定义法(也叫待定系数法)、相关点法(也叫代入法)、交轨法和参数法等，而且还要了解解题过程中产生增解和漏解的原因，掌握避免产生增解和漏解的策略，以达到“会必对，对必全”.