基于主动诱导机制的中继通信智能抗干扰方法

张晓博，王 海，冯智斌，李艾静

（陆军工程大学通信工程学院，江苏南京 210003）

目前已有的中继通信抗干扰研究中，文献［1］针对功率域抗干扰问题，提出了一种以用户为领导者、中继为次领导者、干扰机为跟随者的三层斯坦伯格博弈，证明了斯坦伯格均衡的存在性并求出了均衡解的闭式表达式。文献［2］在前人基础上，进一步考虑了不完全信息对功率策略优化带来的影响。文献［3］聚焦于多中继通信场景，利用Q学习和多臂老虎机方法，实现了用户中继选择和功率控制的联合决策优化。文献［4］研究了扫频、正弦和高斯随机噪声等不同干扰模式下的中继通信选频问题。文献［5］针对非法中继通信链路，提出了主动窃听机制和抗中继选择干扰方法破坏非法通信。文献［6］针对干扰环境下无人机通信网络中的能耗问题，在无先验信息条件下改进了中继功率策略。文献［7］提出了一种基于在线学习的智能抗干扰架构，初步设计了一个抗干扰系统并介绍了系统各功能模块。文献［8］研究了窃听场景下的中继协作安全通信问题。文献［9］研究了多跳中继通信系统中的能效优化问题，考虑功率对能效和传输时延的影响，提出以能效和传输时延为优化对象的多目标优化功率控制算法。文献［10］研究了干扰抑制区下的D2D通信模式选择问题。文献［11］针对常规通信模式易受跟踪干扰攻击的问题，提出了基于双序列跳频的抗干扰通信方法，有效降低了跟踪干扰带来的影响。在车联网背景下，文献［12］进一步考虑外界恶意干扰和用户间互扰带来的影响，联合优化用户的中继选择和波束成形策略，提高控制信息的传输可靠性。上述工作主要针对常规干扰模式或能量受限的反应式干扰，通过功率调整硬抗或跳频躲避的方式实现抗干扰通信，但在面临具有压制能力的跟踪干扰时，传统硬抗方式将不再适用。

在面对跟踪干扰时，可以通过提高跳速的方式躲避跟踪干扰，这是属于硬件设备层面上的改进。针对具有功率压制和环境感知能力的干扰时，文献［13］提出了一种新的合作抗干扰思路，设计了一种面向频谱市场的补偿机制，通过鼓励低通信需求用户成为诱饵，以高功率发送信号主动吸引干扰，从而为其他用户合理配置通信资源。然而文献［13］中需要有一个中心基站为所有用户分配通信策略，且用户与基站之间需要大量的信息交互。

本文针对通信方与干扰方之间的对抗特性以及跟踪干扰被动跟随的特性，构建了基于主动诱导机制的斯坦伯格博弈模型，其中用户作为领导者。所有用户首先选出诱导中继主动释放伪通信信号吸引干扰攻击，随后在剩余可选中继里选择中继进行通信，而干扰机作为跟随者，通过能量检测选择信号能量最大的信道进行干扰，并证明了斯坦伯格均衡的存在性。在该博弈框架下，提出了基于Q学习和随机自动学习机（Stochastic Learning Automata，SLA）的双阶段分层学习中继选择算法。仿真结果表明相比无诱导中继条件下的多用户SLA算法，所提算法能够显著提高用户的平均满意度。

1 多用户多中继通信抗干扰系统

1.1 系统模型

在图1所示的多用户多中继通信抗干扰网络中，存在M个用户收发对，N个中继和一个移动恶意干扰机，考虑所有通信设备都具有单天线且为半双工模式。每个用户都有唯一对应的目的接收端，其目的是在干扰环境中将消息发送至合法接收端。由于远距离条件下信道衰落严重，用户与接收端之间的直传链路不可用，所以用户通过中继转发的方式与目的端进行通信。干扰机始终处于移动状态，且具有信道感知能力和功率压制能力，每次只能在一个信道上释放噪声干扰信号。

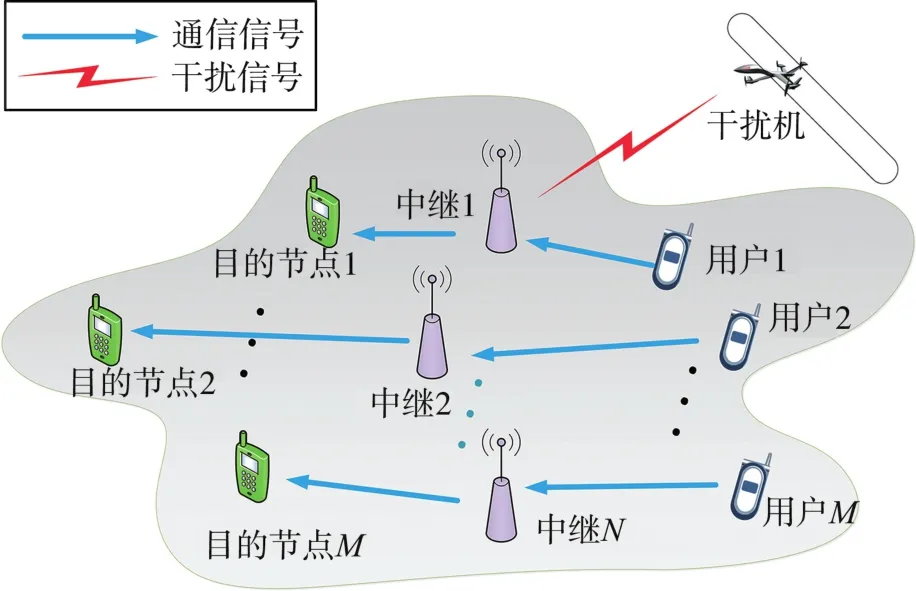
图1 系统模型图

中继通信时隙如图2所示，其中每个时隙包含4个阶段。在第t个时隙里，在阶段1所有用户独立地进行分布式中继选择，并将中继选择结果发送至相关中继。然后在阶段2，用户向各自所选的中继发送消息。在阶段3，中继采用放大转发（AF）的方式重新发送接收到的信息。在最后一个阶段，目标端将当前时隙的信干噪比信息反馈给用户。需要明确的是，在阶段1和阶段4中，用户和接收端分别通过控制信道向中继发送中继选择策略和向用户反馈信干噪比信息，以保证干扰环境下指令信息传输的可靠性。

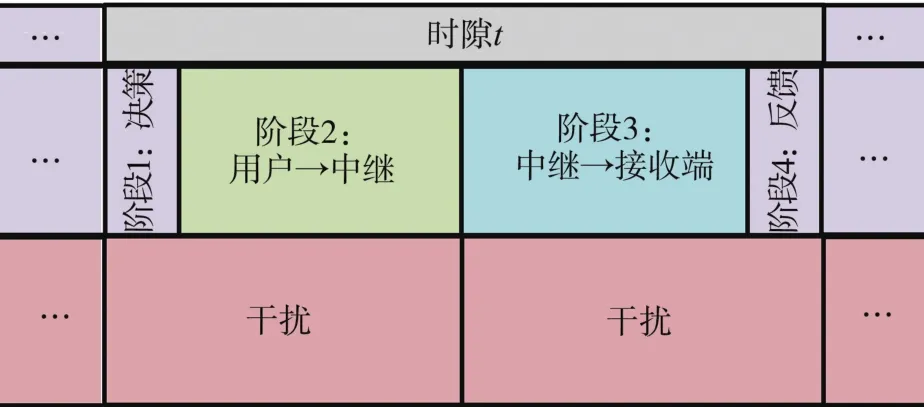
图2 通信时隙图

定义用户集合为 M ＝ ｛1，2，…，M｝， 中继集合为 N ＝ ｛1，2，…，N｝， 共有 N 个信道，可用信道集合表示为N＝｛1，2，…，fN｝，每个中继n工作的信道为fn（该信息固定且任一用户知道每个中继对应的信道）。所有用户的发射功率为Pu，所有中继的转发功率为Pr，Pu、Pr始终保持不变。第m个用户发射端、第n个中继和干扰机的距离分别表示为 dum，j，drn，j。 第m个用户发射端和第n个中继的距离表示为dum，rn，第n个中继和第m个用户接收端的距离表示为 drn，dm。 基于信道衰落模型［14］，上述各通信链路的信道增益分别为其中φ表示路径衰落因子。

1.2 抗干扰问题建模

干扰机能够通过能量检测，选择能量最大的信道进行干扰（只能干扰一个信道）。由于在一个通信时隙内，用户的中继策略传输时间及接收端的反馈时间相比于通信时长可以忽略不计，所以只需考虑干扰机在阶段2和阶段3的影响，其信道干扰策略分别为 fj，1，fj，2， 定义如下

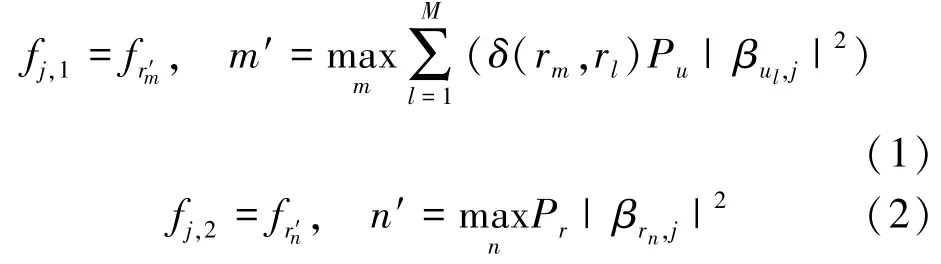
第m个用户的中继选择策略为rm，则第rm个中继接收来自第m个用户信号的信干噪比为

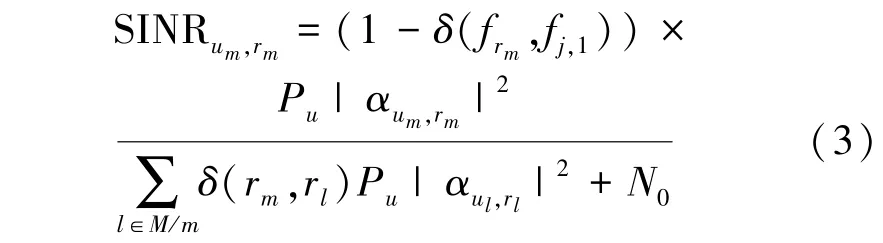
当多个用户选择相同中继时，他们在阶段3将共享时间资源［15］，所以第rm个中继转发来自第m个用户的信号，在第m个用户接收端的信干噪比为

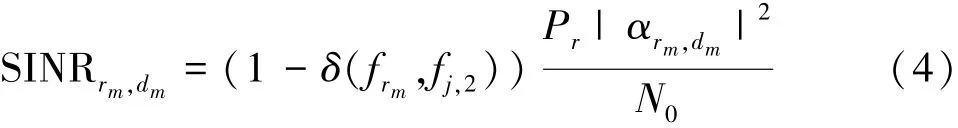
中继采用AF模式，则第m个用户发射端与其接收端之间的传输速率为

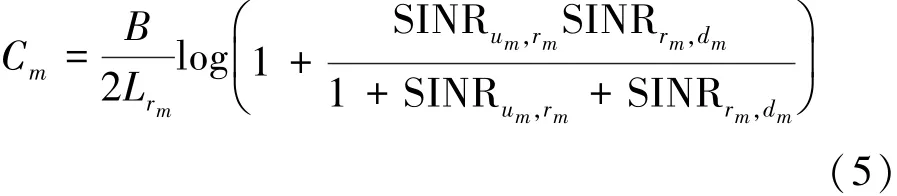
参考文献［16］考虑第m个用户的传输速率需求为C′m，给出第m个用户的传输满意度指标为

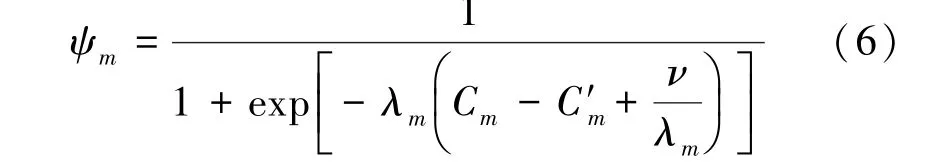
系统的优化目标为最大化所有用户的传输满意度

1.3 双阶段中继选择：主动诱导机制

在具有功率压制能力的跟踪干扰环境下，针对干扰能够检测能量信号最大的信道并被动跟随的特性，提出了一种基于双阶段中继选择的主动诱导机制，在每个时隙选出一个中继主动释放伪通信信号，去吸引干扰攻击，从而使用户能够通过其他中继与接收端进行通信。每个中继既可以转发用户通信信息，也可以主动发送伪造信号吸引干扰机。

在每个时隙初始的用户决策过程中，用户进行双阶段的中继选择。在第一个阶段，所有用户独立决策，任一用户m选出一个中继am去主动吸引干扰，并将各自的选择结果发送给相应中继，中继am只有收到了不少于一半用户数量的请求时，才会认可该请求，并主动释放伪通信信号吸引干扰攻击，则实际上的诱导中继a′定义如下

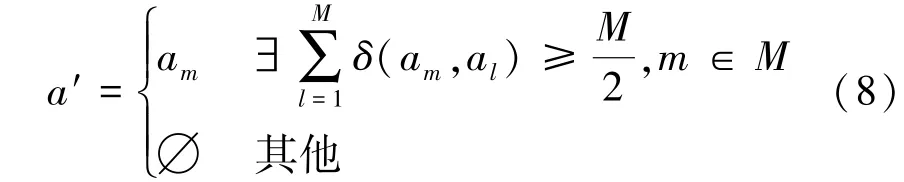
需要注意的是，如果所有中继都没有收到不少于一半用户数量的请求时，那么该时隙没有中继会诱导自己去主动吸引干扰攻击。

在第二个阶段，所有用户进行分布式中继决策，其中用户m在除中继am外的集合中选择中继rm协助通信；如果此时中继rm恰巧为真实的诱导中继a′，那么该时隙用户m则无法获得中继转发服务，即通信失败。

2 斯坦伯格博弈框架下的双阶段中继选择方法

2.1 抗干扰斯坦伯格博弈及均衡存在性证明

在面对跟踪干扰的中继通信场景中，所有用户首先发送消息并选择中继协助转发，随后干扰机通过能量检测对信号强度最大的信道进行干扰。

针对通信方与干扰方之间的对抗特性以及干扰机的被动跟随特性，斯坦伯格博弈作为一种典型的分层博弈可以用来很好地建模该抗干扰问题，其中用户作为领导者，干扰机作为跟随者。所提博弈可以表示为G ＝（A，R，Fj，ψ，V）， 其中A和R 分别表示用户的诱导中继策略空间和通信中继策略空间，Fj表示干扰信道策略空间，ψ和V分别表示用户和干扰机的效用函数。

基于第1节的建模定义，用户和干扰的目标分别为最大化传输满意度和干扰效果。对于跟随者，干扰机通过调整干扰策略以降低通信质量。需要声明的是，在研究干扰类型为跟踪干扰的前提下，干扰机基于感知结果找到干扰信号能量最大的信道，等价于最大化其干扰效用，具体见式（1）。

对于领导者，所有用户通过联合优化诱导中继策略 A ＝ （a1，a2，…，aM） 和通信中继策略 R ＝ （r1，r2，…，rM），最大化整个系统的传输满意度

基于上述分析，在所提斯坦伯格博弈框架下，通过如下分层决策方法解决抗干扰问题

在该抗干扰问题中，考虑用户采用混合策略以增加策略的随机性来欺骗干扰机，从而进一步提高抗干扰性能。令W和P分别表示所有用户的诱导中继和通信中继混合策略集合，即所有用户的双阶段中继策略选择的概率分布。令fj表示干扰机的干扰策略。

定义1如果用户和干扰机都无法单方面地改变策略以提高效用，则策略集 （W∗，P∗，f∗j） 构成斯坦伯格均衡，并满足以下条件

引理1存在一个用户平稳策略和一个干扰机平稳策略，构成斯坦伯格均衡。

证明：受文献［17］的启发，每个有限策略博弈都有一个混合策略均衡［12］，表明在所提博弈中存在斯坦伯格均衡。

对于干扰机，它希望最大化干扰效用函数并进行干扰信道决策

已知干扰机的最优策略，可得用户的双阶段最优中继策略

基于上述分析，策略集 （W∗，P∗，f∗j） 构成斯坦伯格均衡。

2.2 基于强化学习的诱导中继决策

考虑干扰机始终处于移动状态，因为所有中继的转发功率及位置固定，所以干扰机在某一固定位置时感知到的转发信号能量最大的中继也是固定的，但这些信息对己方是未知的。因此，考虑到干扰机在移动过程中的干扰策略和位置之间存在对应关系，将第m个用户的诱导中继选择决策过程建模为一个MDP，即 （Sm，Am，Pm，Rm） ，其中Sm表示第m个用户的状态空间，Am表示其动作空间，Pm表示其状态转移概率，Rm表示回报值。具体定义如下：

（1） 状态空间Sm：fj（k－1） 表示在第k－1个时隙时的干扰所在信道，接收端通过判断信干噪比是否为0和信号分析得出当前时隙的干扰信道，并将其反馈给用户。定义第m个用户在第k个时隙的状态为上一时隙的干扰信道，即 Sm（k） ＝ fj（k － 1） ，用户 m 的状态空间为 Sm＝ ｛fj（1），fj（2），…，fj（k － 1），fj（k），…｝。

（2）动作空间Am：am（k）表示用户m在第k个时隙选择哪个中继去主动吸引干扰，其动作空间为Am＝ ｛am（1），am（2），…，am（k），…｝，am（k） ∈ ｛1，2，…，N｝。

（3） 状态转移概率 Pm：Pm＝ （Sm（k ＋ 1） ｜Sm（k），am（k）），Sm（k ＋ 1），Sm（k） ∈Sm， 表示用户m在第k个时隙从状态Sm（k）选择动作am（k）到达状态Sm（k＋1）的概率。

（4）回报值R：基于接收端的反馈，通过是否有某个用户接收端仍然受到压制性干扰判断诱导中继策略是否成功，即

由于强化学习可以在状态转移概率未知的情况下学习到最优的策略，因此采用强化学习中使用最广泛的Q学习［18］算法来进行决策。在该问题中，所有用户需要在未知环境中不断做出动作以最大化自身长期累积回报，即用户将利用Q学习方法去探索学习干扰机在不同位置上的干扰规律，从而优化诱导中继选择策略。

综上，提出了基于强化学习的诱导中继决策方法。每个用户在执行算法过程中，会维护一张Q值表，以此来评估每个状态下不同动作质量。该算法在每个状态下采取动作并获得回报值，从而更新相应的Q值，经过多次迭代循环直至收敛到最优诱导中继选择策略，Q函数可表示为

其中，α表示学习速率，γ表示折扣因子，α，γ∈［0，1］。 Rk表示当前 Sk状态的回报值， a～为状态Sk＋1下的所有可选的诱导中继策略。用户在选择并执行动作ak后，在k＋1时隙到达Sk＋1状态。策略选择概率向量 Wm（k） ＝ （w1（k），…，wN（k）） 的更新公式为

其中，θ表示玻尔兹曼系数常量，wn（k＋1）表示在第k＋1个时隙用户选择第n个中继作为诱导中继的概率。

2.3 基于随机自动学习机的通信中继决策

各个用户在选出诱导中继后，再运行分布式决策算法，从剩余的可选中继选出合适的通信中继。受随机自动学习机［19］的启发，考虑到不同诱导中继策略下用户可选中继集合不同，提出了基于多模SLA的中继选择算法。

以用户在第k个时隙已经选出中继n作为诱导中继为例，此时用户可选中继集合为｛1，2，…，n－1，n ＋ 1，…，N｝，定义此时的模型状态为En，记Pn＝［p1；p2；…；pm；…；pM］为所有用户的中继选择混合策略， pm＝ ［pm，1，…，pm，n－1，pm，n＋1，…，pm，N］表示第m个用户选择各个中继的概率，pm，n－1表示第m个用户选择第n－1个中继的概率。

在当前模型状态En下，所有用户分别基于各自的中继选择策略进行通信，并在每个时隙末端，用户能够接收到来自对应接收端的信道传输速率作为反馈信息，基于当前的回报值，用户对中继选择的混合策略进行如下更新

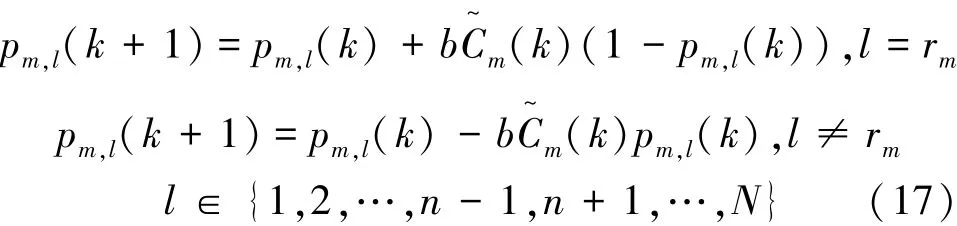
其中，0＜b＜1为迭代步长，C～m为归一化传输速率，表示为

需要声明的是，每个用户基于当前选择的诱导中继，调用对应模型状态下的中继选择混合策略，进行中继选择并基于反馈结果更新混合策略。而其他诱导中继状态下的混合策略不会被调用和更新。

3 仿真结果与分析

采用MATLAB对所提算法进行仿真，设置4个用户、4个中继、4个信道，初始化各类信道参数。背景噪声密度为－174 dBm／Hz，所有用户的发射功率为23 dBm，所有中继的发射功率为30 dBm，每个信道的带宽为1 MHz，用户的传输速率需求为1 Mb／s，路径衰落因子φ＝2。

系统分布如图3所示，存在4个用户、4个中继和一个干扰机。用户1到用户4的发射端和接收端分别位于（0.5 km，4.5 km）、（0.5 km，3.5 km）、（1 km，4 km）、（1.5 km，4 km）和（4 km，1.5 km）、（3.5 km，0.5 km）、（3.5 km，1 km）、（3.5 km，1.5 km），中继1到中继 4分别位于（1.5 km，2.5 km）、（2 km，3 km）、（2.5 km，3.5 km）、（2.5 km，3 km）。 干扰机的起点和终点分别为（3.5 km，4 km）和（4 km，3 km），并以10 m／s的速度在两点之间往返移动。红色箭头代表干扰信号，蓝色箭头代表通信信号。

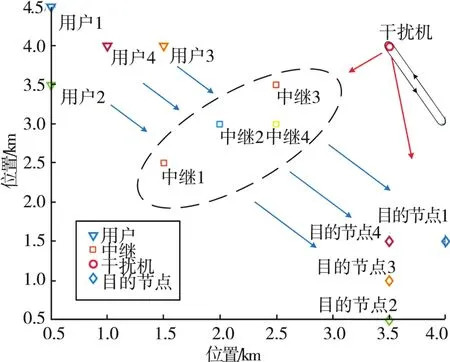
图3 系统分布图

图4给出了用户1的诱导中继选择概率，且所有用户能够达成基本一致的诱导中继策略。从图4中可以看出，随着时间的推移，用户会主动调整诱导中继选择概率，即在不同时段，用户会倾向于选择不同的诱导中继。这是因为干扰机始终处于移动状态，在不同位置上，干扰机感知到通信信号能量最大的信道不同，其干扰策略也会发生改变，所以需要改变诱导中继策略以达到吸引干扰的效果。

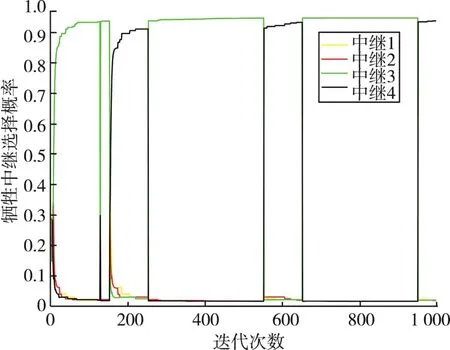
图4 诱导中继选择概率

图5、6分别给出了在不同诱导中继策略下，用户1的通信中继选择概率。从图5可以看出，当诱导中继为第3个中继时，用户1更倾向于选择中继4进行协助传输。从图6可以看出，当诱导中继为第4个中继时，用户1更倾向于选择中继2进行协助传输。结果表明，所提多模SLA中继选择算法可以使所有用户在不同诱导中继选择策略下分开更新其中继选择概率并各自达到收敛，从而找到不同状态下所有用户的通信中继选择策略。

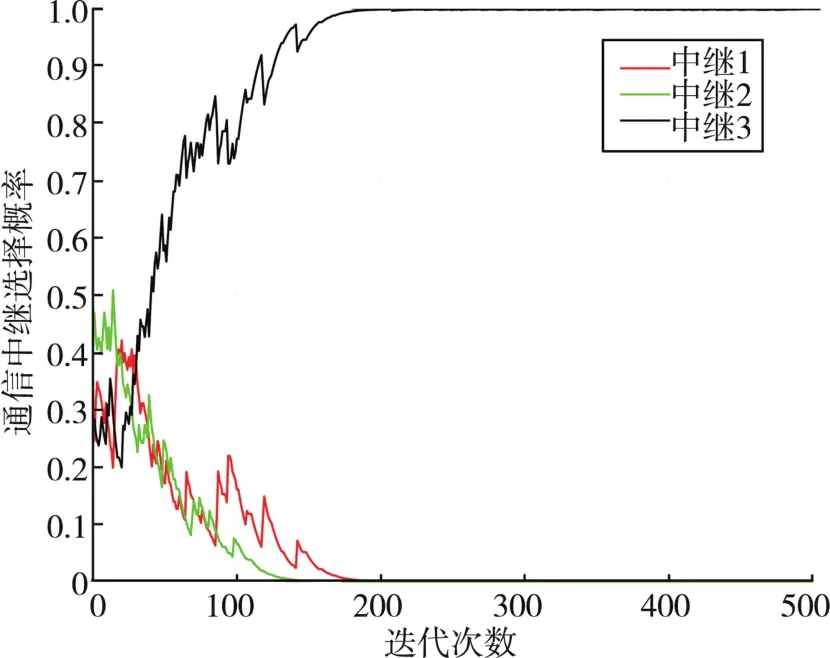
图5 第3个诱导中继下用户1的通信中继选择概率

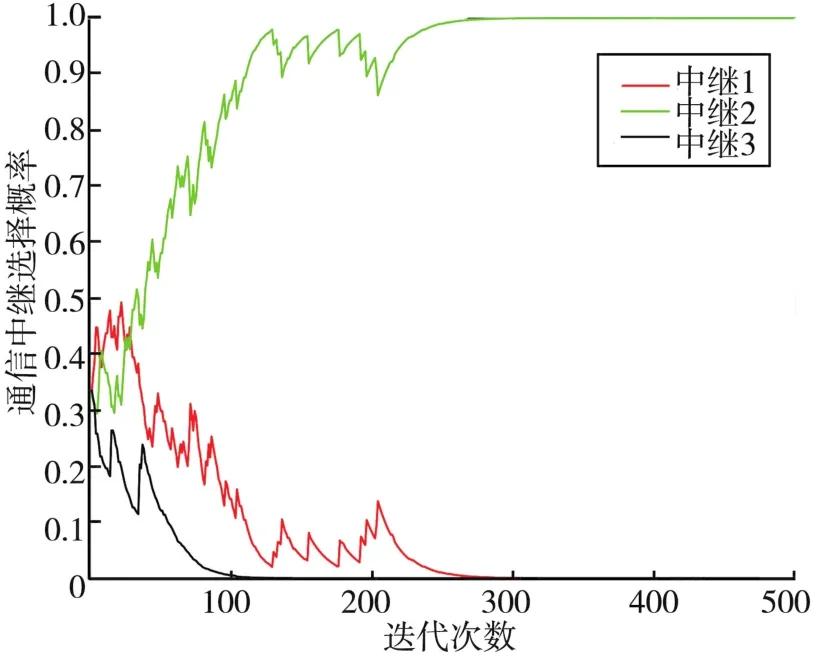
图6 第4个诱导中继下用户1的通信中继选择概率

图7给出了无诱导中继策略下用户1的通信中继选择概率。从图7可以看出，用户1在学习过程中以较大概率交替选择中继3和中继4，并最终收敛至选择中继3进行通信。结合图3的系统分布和图4诱导中继选择概率可以看出，此时用户1大部分时间都会被干扰攻击，进而导致通信效用显著降低。

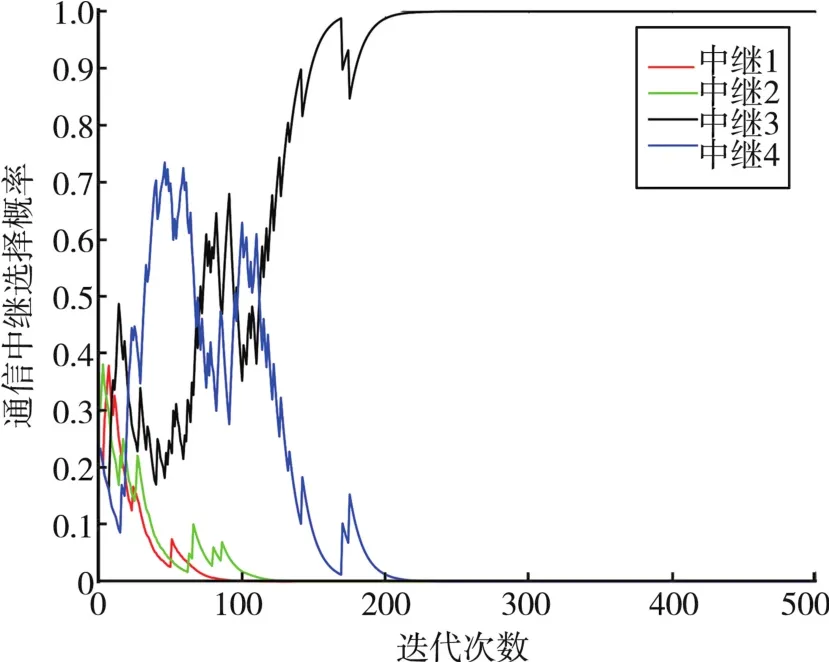
图7 无诱导中继下用户1的通信中继选择概率

根据图3所示的系统分布图，对干扰机的移动轨迹进行等分取点，分别设点（3.5 km，4 km）、（3.625 km，3.75 km）、（3.75 km，3.5 km）、（3.875 km，3.25 km）和（4 km，3 km）为位置 1、位置2、位置3、位置4和位置5，并给出了无诱导中继下的用户满意度，如图8所示。所有用户基于SLA算法进行分布式中继选择，在没有诱导中继的条件下，每次至少存在一个中继的转发信息被干扰机干扰，所以图中存在用户1和用户4满意度为0的情况。具体体现为随着干扰策略的改变，在位置1、位置2和位置3时，用户1受到干扰且其满意度为0，而在位置4和位置5时，用户4受到干扰且其满意度为0，而其他未受干扰用户的满意度较高。

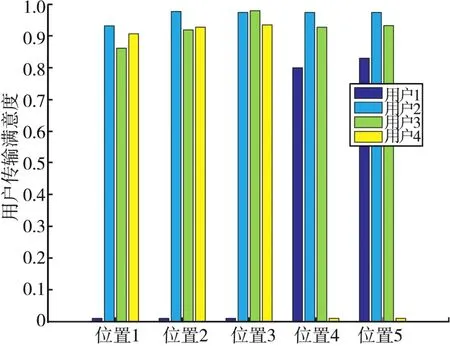
图8 无诱导中继下的用户满意度

图9给出了有诱导中继下的用户满意度。从图9中可以看出，由于有诱导中继的存在，能够使其他所有用户⁃中继通信对都不受到干扰的影响，但存在多个用户选择相同通信中继的情况，如在位置1、位置2和位置3时，用户1和用户3选择了相同中继，所以他们的传输满意度相较于用户2和用户3比较低；同理，在位置4和位置5时，用户1和用户4也选择了相同中继，所以满意度相对较低。但整体与无诱导中继情况相比，所提算法能够保证在干扰策略发生变化的情况下，所有用户的满意度始终维持在较高的水准。

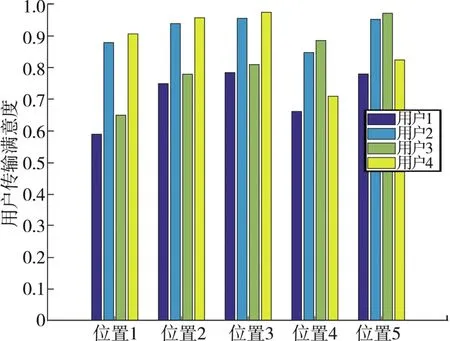
图9 有诱导中继下的用户满意度

图10记录了整个迭代过程中用户的平均满意度，并给出4个中继条件下用户满意度随用户数量变化的情况。图10中紫色柱和绿色柱分别表示有诱导中继条件下，所有用户的平均满意度和所有用户中平均满意度最低的用户的值；蓝色柱和黄色柱分别表示无诱导中继条件下，所有用户的平均满意度和所有用户中平均满意度最低的用户的值。从图10中可以看出，诱导中继的存在能够使用户的平均满意度提高20%以上，并避免某一用户的平均满意度过低的情况，在中继数量保持不变的前提下，随着用户数量的增加，所提算法依旧能够保证较好的性能。

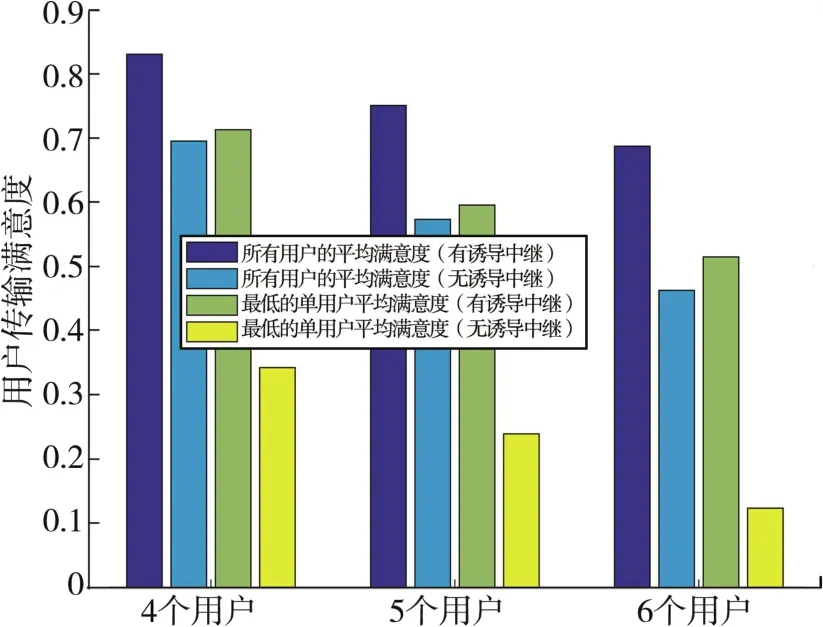
图10 用户满意度性能对比示意图

4 结束语

针对跟踪干扰环境下的抗干扰中继优化问题，构建了基于主动诱导机制的斯坦伯格博弈模型，用户作为领导者，利用其先发制人的优势，通过选出诱导中继去主动吸引干扰攻击，保障其他中继能够可靠通信。提出了基于Q学习和随机自动学习机的双阶段中继选择算法。仿真结果表明相比无诱导中继条件下的多用户SLA算法，所提算法能够显著提高用户的平均满意度，并避免了某一用户的平均满意度过低的情况，尽可能地保证所有用户的通信需求。