理想及其算法设计

宗 慧，曹子宁，王福俊

（南京航空航天大学计算机科学与技术学院，江苏南京 211106）

随机数在统计理论、科学研究和工程设计中具有重要作用［1］。尽管在真实的物理世界中可以得到随机数，但限于生成速度和生成方法，真随机数的获取极为困难。随着电子数字计算机的问世，采用算法产生随机数成为一种行之有效的方法，所产生的这些数字称作伪随机数。当今随机数在现代科学中的应用非常广泛，如计算科学、通信、网络安全、雷达探测、统计分析、数值模拟等领域都有大量的应用［2－3］。 然而，伪随机数发生器的质量对这些应用的成效至关重要。因此，伪随机数发生器质量受到科技界的关注。德国Federal Office for Information Security （Bundesamt für Sicherheit in der Informationstechnik，BSI）评估随机生成器质量的主要准则要求所产生的序列的相同概率低，符合统计学的平均性。美国国家标准与技术研究院（National Iustitute of Standardsand Technology，NIST）侧重于数学性能而制定了随机性测试方法，主要包括对频数、块内频数、矩阵秩、离散傅里叶变换以及几种组合的测试［4］。 根据 BSI主要准则，文献［5］利用 Monte Carlo计算值的方法建立了一种评价伪随机数发生器质量的方法，该方法将理想π值作为标准，以实际计算出的值与其之差评价了多种伪随机数发生器的质量。

1 面积之比——计算的基本思想

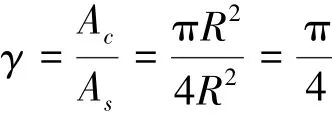
因此

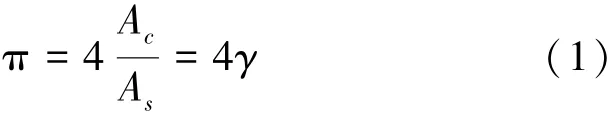
含有内切圆的正方形如图1（a）所示。如果该正方形由N2个面积为1的小正方形组成，那么正方形的面积就等于所有小正方形的面积之和，即As＝N2。

如果把图1（a）中的每个小正方形用点来替代，如图1（b）所示，那么点的数量之和就等于正方形的面积，如果把点看作单位1，当点足够小，且当相邻的两点的距离趋于零时，那么区域内点的数量之和就可以等价于该区域的面积，以此类推，根据式（1）知：计算值时，只需要计算内切圆面积Ac与正方形面积As之比。因此，可以先将图1（a）中的所有小正方形缩为图1（b）中的点，当相邻两点的距离趋于零时，就可以用内切圆和正方形内的点分别代替式（1）中的Ac和As进行计算。这就可以在程序中方便地以点代面实现对值的计算，从而避免了程序从面的角度计算π值的困境。

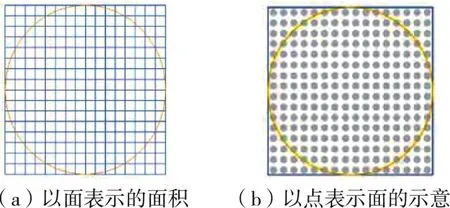
图1 以点代面的原理

定义1给定一个由均匀分布的充分多的点组成的含有内切圆的正方形，并设正方形内的点数为Xs，内切圆内的点数为 Xc，有

定理1

为了使证明简洁，先回忆一下数学中对点、线和数轴的有关描述。

点是没有部分的，即它只表示位置而无大小。两个不同的点可以确定一条直线［15］。如果在直线上确定一个点O为原点，并指定一个方向为正向，则该直线为数轴，显然数轴是由点的集合构成的。数轴上的每个点当且仅当对应一个实数。由于实数是稠密的，即任意两个不同的实数间必存在另一个实数，所以数轴上的点是稠密的。又由于实数集是无限集，所以实数上的点集也是无限集。

证明：根据定义1，设含有内切圆的正方形的边长为R，并构成如图2所示的直角坐标。此时的3个点（0，0），（0，R）和（R，0）就确定了一个平面。 在向该平面内的正方形投放均匀分布的充分多的点时，就可以由点数计算值。然而，只有在这些投放的点是稠密的，即是无限时，才能得到与理论一致的值，即

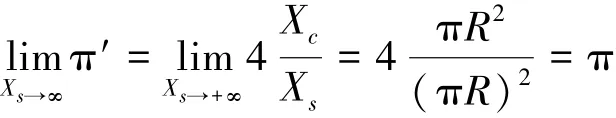
图2 边长为R的正方形所在的平面

利用式（2）进行计算，正方形内必须具有一定的点数，才能得到满足所要求精度的′。例如，正方形内只有100个点，显然，此时计算出来的′与理论值的误差很大，因此使用较少的点取代面积来计算′没有意义。那么在正方形内投放多少个点才是有意义的呢？这是本文要解决的关键问题。下面就此进行讨论。

定义2给定一个由102r个均匀分布的点组成的含有内切圆的正方形。称圆内的点数为理想点数，记作XI；由该图形求出的′称作理想，记作I，且

定理2给定一个由102r个均匀分布的点组成的正方形，并设I与π的计算误差为10－m，其中m＞0，有

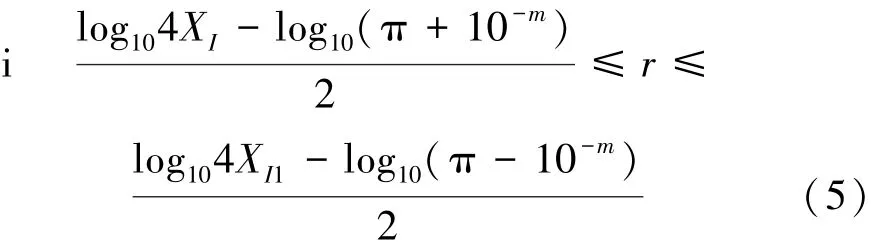
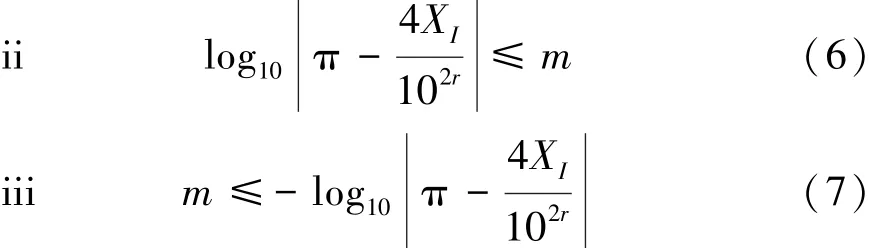
证明：（i）假设落入正方形内点数为102r，并设

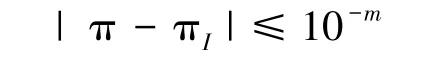
即

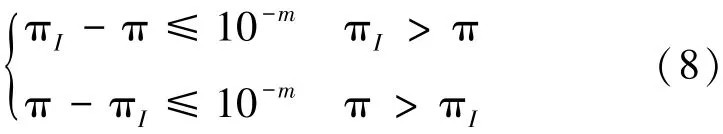
根据式（4），有

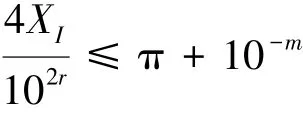
即

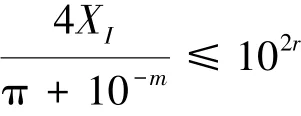
两边取对数，有

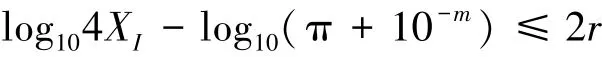
故

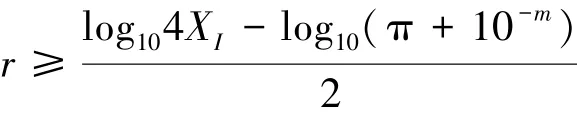
根据式（4），有

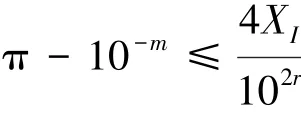
即

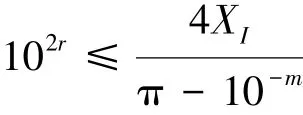
两边取对数，可得

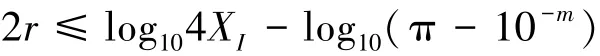
故

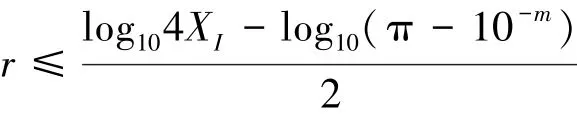
根据（a）和（b），式（5）得证。

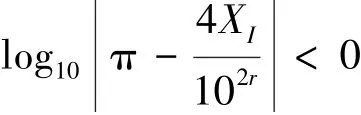
故m ＜0，与定理2所给条件矛盾。

（iii）的证明与（i）类似，略。

定理2表明了r与m之间的关系。根据定理2可知，当正方形内点的数量给定，那么I与的计算误差就可以得到，同时I的精度也就确定了。

3 计算πI的算法设计

为了减少计算量，在算法设计时取如图3（a）所示的含四分之一内切圆的正方形计算I值，首先在正方形内均匀地投放n2个点，这里的 n＝10r；然后统计内切圆内点的总数，最后根据式（4）计算I。

（count＝0） ∥count为内切圆内点数之和

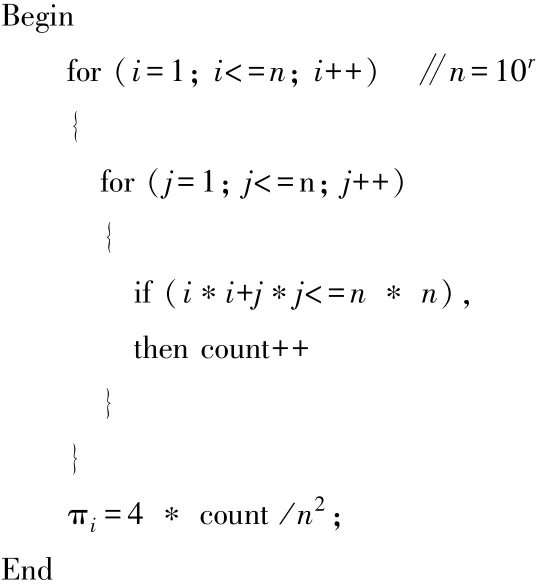
在这个算法中采取的是利用循环结构依次统计内切圆内的所有点，如果投放的点数非常多，那么统计的点的数量也会加大，从而导致运算的时间变长，因此本文对这个算法进行了改进以缩短计算时间。如图3（a）所示，可以统计正方形内内切圆外的灰色点的数量，记为Yc，这个点的数量是明显少于内切圆内的点的数量Xc的，所以同样投点的情况下，计算的次数减少了，计算的时长也缩短了，但是这种算法减少的计算次数还不是特别显著。在此基础上本文又做了一个改进，依然是统计 Yc，如图 3（b）所示，正方形的对角线与内切圆的交点位于坐标（0.707 106 78n， 0.707 106 78n）处，因此只需要统计S1区域内的点数 S1＿count，而 S2区域内的点数是可以根据直接计算得到，记为S2＿count，然后可以得到 Yc＝ 2S1＿count＋S2＿count，按照这个思想设计的算法运算的次数大幅度降低，计算的时长也缩短了。

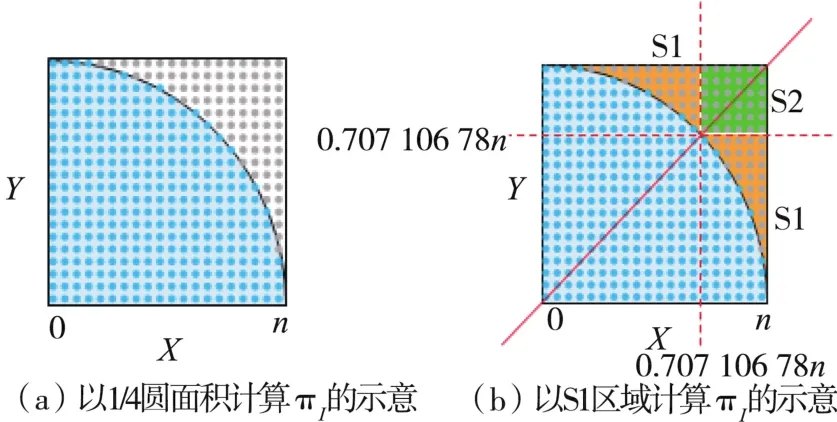
图3 计算πI的算法设计

具体算法如下：

（S1＿count＝0） ∥S1＿count为内切圆外S1区域内点数之和

4 实验结果与分析

依据表1可以看出：

表 1 不同的投点数对应的I值（π＝3.141 592 653 6……）

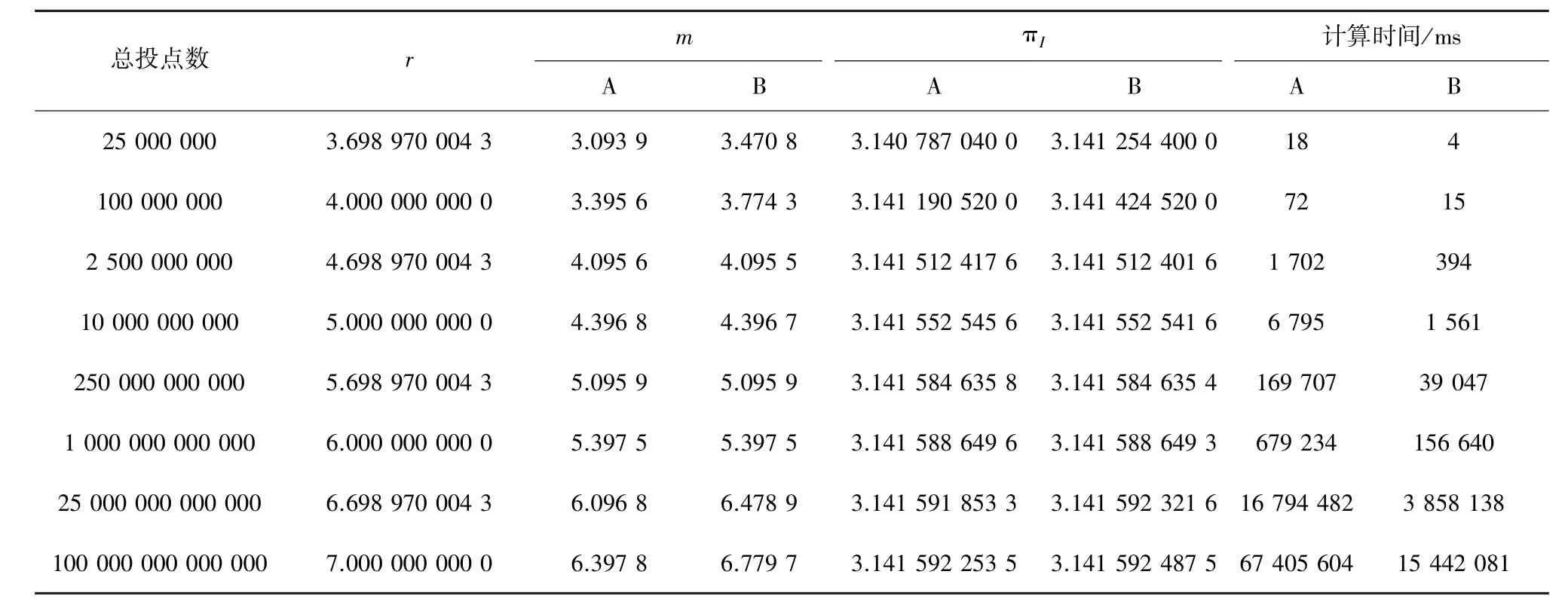
表 1 不同的投点数对应的I值（π＝3.141 592 653 6……）

注：列A表示IDEAL＿1算法实验结果，列B表示IDEAL＿2算法实验结果

总投点数 r m πI 计算时间／ms A B A B A B 25 000 000 3.698 970 004 3 3.093 9 3.470 8 3.140 787 040 0 3.141 254 400 0 18 4 100 000 000 4.000 000 000 0 3.395 6 3.774 3 3.141 190 520 0 3.141 424 520 0 72 15 2 500 000 000 4.698 970 004 3 4.095 6 4.095 5 3.141 512 417 6 3.141 512 401 6 1 702 394 10 000 000 000 5.000 000 000 0 4.396 8 4.396 7 3.141 552 545 6 3.141 552 541 6 6 795 1 561 250 000 000 000 5.698 970 004 3 5.095 9 5.095 9 3.141 584 635 8 3.141 584 635 4 169 707 39 047 1 000 000 000 000 6.000 000 000 0 5.397 5 5.397 5 3.141 588 649 6 3.141 588 649 3 679 234 156 640 25 000 000 000 000 6.698 970 004 3 6.096 8 6.478 9 3.141 591 853 3 3.141 592 321 6 16 794 482 3 858 138 100 000 000 000 000 7.000 000 000 0 6.397 8 6.779 7 3.141 592 253 5 3.141 592 487 5 67 405 604 15 442 081

表2 不同有效位的理想值对应的最低投点数

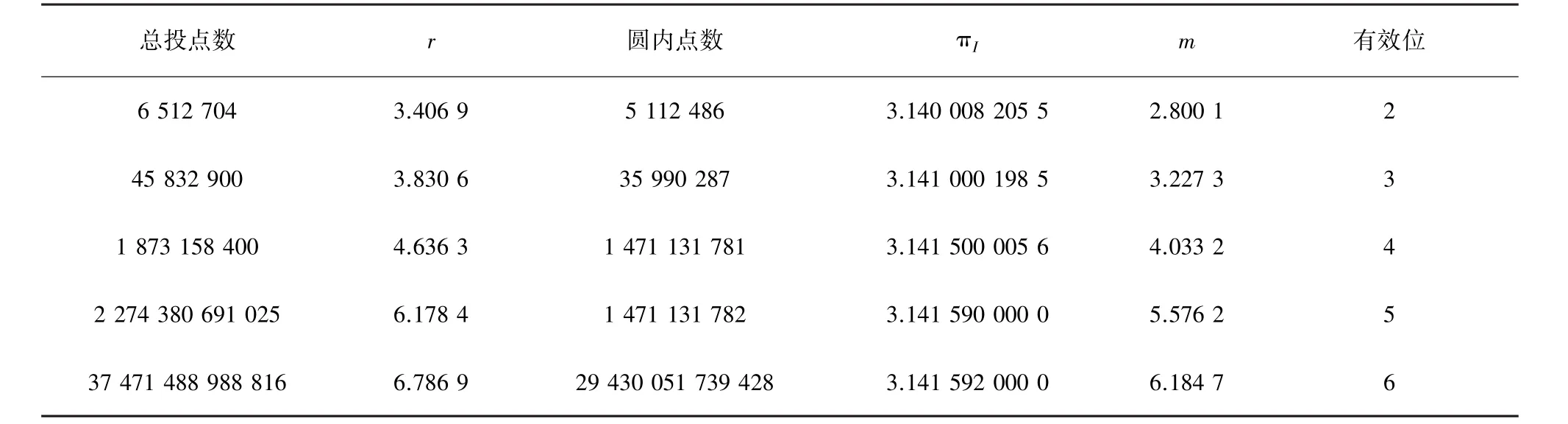
表2 不同有效位的理想值对应的最低投点数

总投点数 r 圆内点数 πI m 有效位6 512 704 3.406 9 5 112 486 3.140 008 205 5 2.800 1 2 45 832 900 3.830 6 35 990 287 3.141 000 198 5 3.227 3 3 1 873 158 400 4.636 3 1 471 131 781 3.141 500 005 6 4.033 2 4 2 274 380 691 025 6.178 4 1 471 131 782 3.141 590 000 0 5.576 2 5 37 471 488 988 816 6.786 9 29 430 051 739 428 3.141 592 000 0 6.184 7 6

最后本文结合表1和表2中的数据，绘制了r和m之间的关系，如图4所示。根据该图可以得到m值随着r值的增长而增长。图4中的曲线显示，对于投点数（10r）2和精度（10－m）之间的关系，IDEAL＿1和 IDEAL＿2两种算法的结果是一致的。

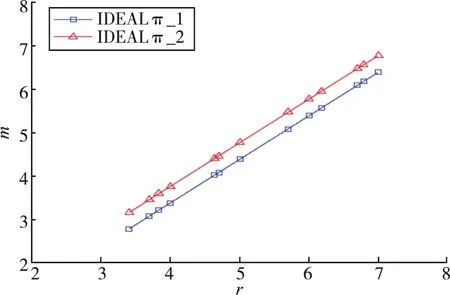
图4 投点数（10r）2和精度（10－m）之间的关系

5 结束语

也可以用其他需要用到随机数发生器计算的常数或诸如面积、体积之类的方法去评价伪随机数发生器，比如e，这是一种比较简便的方法。