改进型有限分析法模拟包气带土壤水分运移
2021-11-24张在勇王文科陆彦玮宫程程武泽宇
张在勇,王文科,陆彦玮,宫程程,冉 彬,武泽宇
•农业水土工程•
改进型有限分析法模拟包气带土壤水分运移
张在勇,王文科※,陆彦玮,宫程程,冉 彬,武泽宇
(1. 长安大学旱区地下水文与生态效应教育部重点实验室,西安 710054;2. 长安大学水利与环境学院,西安 710054)
近年来有限分析法被广泛应用于模拟土壤水分运移。混合型有限分析法通常使用一阶有限差分近似代替Richards方程中的时间导数项。尽管这种方法与其他的数值方法(例如有限差分法)相比,能获得精确度更高的数值解,但是当需要精细刻画陡峭湿润锋面向下传输过程时,需要对时间项的处理提出更高的要求。因此,该研究提出一种从时域和空间域获取局部解析解的改进型有限分析计算格式来克服上述问题。将改进的有限分析法的数值解、混合型有限分析的数值解、有限差分数值解与解析解定量化对比研究发现,改进型有限分析计算格式在较大空间步长条件下(空间步长为10 cm),能够获得精度较好的数值解,且能更好地控制质量平衡误差。此外,改进的有限分析法能获得与现有的软件(VSAFT2)相似的计算结果。该研究能为包气带水分运移模拟提供一种可靠的方法,推动区域土壤水资源的评价与管理。
土壤;水分;运移;有限分析法;包气带;数值模拟
0 引 言
包气带作为大气降水、地表水、包气带水和地下水迁移转化的核心区域,是研究地下水补给和排泄的关键[1]。精确描述土壤水动态过程,对于农田水利、水文、生态等领域具有重要意义。然而,描述包气带水分运移的Richards方程[2]和参数(如渗透系数、容水度)具有高度的非线性[3-4]。因此,直接求取其解析解极其困难[5]。通常情况下,需要使用数值模拟方法模拟包气带水分运移。在众多数值模拟方法中,应用最广泛的是有限差分法和有限元法[6-8]。为了提高有限差分法和有限元法的计算精度,通常需要增加计算节点的数量。但是,增加计算节点很容易导致计算速度大幅度下降,特别是处理复杂的三维水流和溶质运移问题。此外,在选取不适当的空间和时间步长时,这两种方法常常容易发生数值震荡、数值弥散及质量不守恒等一系列问题[5,9-10]。
近年来,基于解析解发展起来的有限分析数值法[11]被广泛应用于解决环境和资源等领域的问题。例如,Chen等[11-12]使用有限分析法求解Navier-Stokes方程。Hwang等[13-14]应用有限分析法模拟地下水中的溶质运移。王文科等[15-16]应用有限分析法模拟地下水流问题。Zhang等[1,17-20]使用有限分析法模拟包气带中的水分运移。有限分析法不同于有限差分法和有限元法,它既不像有限差分法采用差分格式代替微商,也不像有限元法使用插值函数近似支配方程,而是通过局部解析解组成整体数值解。因此,有限分析法不仅结合了数值方法的灵活性,而且具有解析解的优点,所获得的截断误差最小,并且能够保持极好的数值稳定性[21]。
在适当的初始条件和边界条件下,有限分析法可以通过以下两种方式获得局部解析解[22]:1)使用差分格式处理Richards方程中的时间项,然后再推导局部单元格的解析解,即仅获取空间项的解析解,该方法被称为混合有限分析法[13];2)直接使用局部单元格的初始条件和边界条件获取Richards方程的解析解,即同时获取空间项与时间项的解析解。
尽管Zhang等[19]研究表明,使用混合有限分析法在一定程度上可以获得满意的数值解。但是当需要精细刻画陡峭湿润锋面向下传输过程时,对时间项的处理提出了更高的要求。为了克服差分格式引入较大计算误差的问题,Tsai等[18]首次提出采用时间权衡因子的有限分析法来提高计算精度。但是这种处理方法在计算过程中需要预估参数,且在处理三维水流问题时特别耗时。除此之外,为了避免使用差分代替微分带来的误差,Wang等[14]采用拉普拉斯变换处理时间项。该方法虽然可以获得满意的结果,但是同样存在缺陷,例如它只能处理线性方程并且难以应用于多维问题等。
目前,国内外对基于第二种局部解析解的有限分析法模拟包气带水分运移鲜有报道。本文推导了基于第二种局部解析解的有限分析计算格式,求解Richards方程,即同时获取空间项与时间项的解析解。首先,运用局部单元格的初始条件和边界条件推导有限分析计算格式。其次,通过解析解验证该有限分析计算格式的计算精度问题及质量平衡误差问题。再次,将推导的有限分析计算格式获得的数值解与有限差分法和混合型有限分析计算格式的数值解对比。最后,针对实例,对比改进的有限分析数值法获得的数值解和基于有限元法发展起来的现有软件(VSAFT2)[23]计算结果。该研究旨在为包气带水分运移模拟提供一种可靠途径,推动区域土壤水资源的评价与管理。
1 改进型有限分析法
本文基于混合型有限分析计算格式[19],改进对方程中时间项的处理,推导同时包含时间项和空间项解析解的有限分析计算格式,即改进型有限分析计算格式。
均质土壤一维水分运移方程[2]为
注:WC,EC,SW,SE和SE分别表示局部单元格节点相对位置。为时间,h;为单元格节点;为当前时刻;为空间步长,cm。
Note: WC, EC, SW, SC, and SE indicate the relative position of the local element.is time, h;is element node;is current time;.is spatial discretization, cm.
图1 有限分析法局部单元格
Fig.1 Local element of the finite analytic method
非饱和带渗透系数和土水特征曲线用Gardner模型[24](式(2)和式(3))计算。

基于Gardner模型将式(1)变为
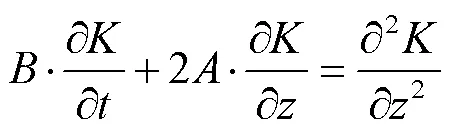
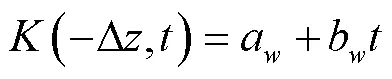
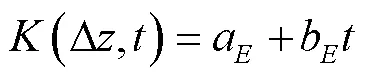
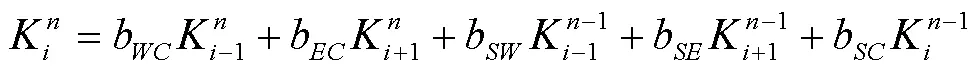
一般来说,计算域中的每个节点都可以推导一个与方程(9)一样的计算格式。本文案例中,这种计算格式与边界条件组成一个方程组之后,使用超松弛迭代法(Successive Over Relaxation,SOR)计算数值结果。此外,时间步长采用变步长方法,每次迭代误差设置为10-4。
2 模型应用案例
2.1 案例
2.1.1 案例一
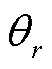
为了更好地说明改进的有限分析法获得的数值解的优越性,本文也将混合型有限分析法的数值解[15]和有限差分数值解与解析解进行对比,选取3种不同的空间步长(1、5和10 cm)模拟上述算例。
2.1.2 案例二
为了更好地检验改进的有限分析法的适用性,将改进的有限分析法获得的数值解与基于有限元法发展的软件VSAFT2的数值模拟结果进行比较。VSAFT2是美国亚利桑那大学T.-C. Jim Yeh教授团队开发的模拟软件[23],主要用以饱和-非饱和流、溶质运移过程的数值模拟以及水力层析抽水试验的渗透系数反演。
边界条件如下:
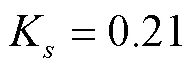
2.1.3 案例三——变边界条件下
求解非饱和水流运动方程数值的难点在于上边界降雨蒸发的影响,非饱和带水分运移呈现出强烈的非线性。本文选取陕北风沙滩地区实际蒸发量和降雨量作为上边界条件,土壤参数和案例二一致。边值条件如下:
式中和分别代表降雨量(cm/d)和蒸发量(cm/d)。
2.2 评价指标
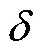
式中0和M分别代表在零时刻和时刻的总水量,cm。
3 结果与分析
3.1 改进型有限分析数值解与其他数值方法的比较
改进型有限分析数值解、混合有限分析数值解、有限差分数值解与解析解在1、5、10、20、30和100 h的比较如图2所示。从图中可以看出,当空间步长为1 cm时,3种数值方法与解析解的拟合程度非常好(图2a~图 2c)。当空间步长增加到5 cm时,除了在入渗初期湿润锋面处会引起相对较大的误差外(特别是有限差分数值解(图2f),误差较大),其他时期均可以获得与解析解相一致的结果。但是,当空间步长为10 cm时,与解析解相比,混合有限分析数值解明显偏大,有限差分数值解明显偏小,改进型有限分析数值解除了在入渗初期(=1 h)外,总体可以获得满意的结果。总的来说,在空间步长较小时,3种数值方法都可以获得满意的结果。当选取较大的空间步长时,改进型有限分析法可以获得最好的数值解,混合有限分析法次之。
为了更好地说明3种数值方法的计算精度,图3显示了3种数值方法在1、5、10、20、30和100 h剖面负压的局部单点误差。从图3可以看出:当空间步长为1 cm时,改进型有限分析法和混合有限分析法获得的结果相当,最大的局部单点误差不超过0.6%(图3a和3b)。然而,有限差分法在入渗初期(=1 h)的误差超过6%。当空间步长为5 cm时,改进型有限分析法和混合有限分析法计算的局部单点误差相似,最大的局部单点误差不会超过7%(图3d和3e)。然而,有限差分法计算的局部单点误差在入渗初期(=1 h)超过了30%。最后,当空间步长为10 cm时,改进型有限分析法在入渗初期的最大局部单点误差为16.4%,并且随着时间的增加,最大局部单点误差迅速降到10%以下(图3g)。混合有限分析法在入渗初期(=1 h)的最大局部单点误差超过了40%(图3h),随着时间的推移,局部单点误差减小的幅度小于改进型有限分析法。但是,有限差分法在入渗初期(1h)的最大局部单点误差超过60%(图3i),并且误差随着时间的推移缓慢减小。总体而言,选取的空间步长较小时(1和5 cm),改进型有限分析法和混合有限分析法都能够获得满意的结果,计算的局部单点误差远小于有限差分法。当选取空间步长较大时(10 cm),改进型有限分析法可以获得最好的结果,混合型有限分析法次之。
图4 a~图4c分别显示了改进型有限分析法、混合有限分析法和有限差分法在空间步长为1、5、10 cm的质量平衡误差。当空间步长取1 cm时,3种数值方法最大的质量平衡误差不超过0.14%、0.5%和3.7%。当空间步长为5 cm时,最大的质量平衡误差不超过1.6%、2.3%和13.9%。当空间步长为10 cm时,最大的质量平衡误差不超过6.3%、49.5%和25.6%(注意,混合型有限分析法只有在初始时刻的质量平衡误差稍微高于有限差分法,图 4c所示)。综上所述,改进型有限分析法可以最好地控制质量平衡误差,其次是混合有限分析法,最后是有限差分法。
3.2 改进型有限分析法与VSAFT2软件求解结果对比
改进型有限分析法与VSAFT2软件在1、10、40和100 h的计算结果如图5所示。由图5可看出,改进型有限分析法的数值解与VSAFT2软件计算结果基本一致。从而说明改进的有限分析法能够获得与VSAFT2软件一致的数值结果。由于该算例没有解析解进行对比,所以无法分析局部单点误差和质量平衡误差。
图6显示了陕北风沙滩地区实测的蒸发量和降雨量。前7天为晴天,后3天均有降雨,其中最大的降雨量为0.25 cm/d。从图可知,发生降雨事件以后,蒸发量减小。6月1日、2日、8日和10日改进型有限分析法计算的负压值与VSAFT2软件计算结果如图7所示。第1天负压相对较小,随着蒸发不断进行,剖面负压随之减小。对比VSAFT2软件计算结果,改进型有限分析法可以用于模拟降雨和蒸发过程中非饱和带水分运移。

a. 06-01b. 06-02c. 06-08d. 06-10
4 讨 论
Tsai等[17]研究表明,使用混合有限分析数值法求解负压型Richards方程时虽然可以获得稳定的数值解,却并不能有效控制质量平衡误差,在模拟非饱和带水分运移过程时,陡峭的湿润锋面常常会影响计算精度。Tsai等[18]发现使用混合型有限分析数值法求解负压型Richards方程时,使用较小的空间步长时可以获得满意的结果,当采用较大的空间步长时难以获取较为满意的数值解。为了进一步的提高混合型有限分析数值法的计算精度,Zhang等[1]提出基于Kirchhoff变换的混合型有限分析数值法模拟包气带水分运移。该方法在一定程度上可以提高计算精度,但是在选取较大的空间步长条件下仍然可能会引起较大的质量平衡误差。主要原因在于混合型有限分析法中使用一阶有限差分近似替代时间项时可能会引起数值扩散,特别是在选取大的空间步长时。本文提出改进型的有限分析法具有明显的优势在于从时间和空间域都找到了局部解析解,所以能够获得更高精度的数值解。
在使用相同的计算网格条件下,改进型有限分析法相比较于有限差分法能够获得更加精确的数值解且能够更好控制质量平衡误差。总的来说,改进型有限分析法优于有限差分法主要有以下几个因素:1)改进型有限分析法直接获得控制方程的解析解,从而完成了微分方程和相关边界条件的数值离散。因此获得的计算格式具有微分方程的性质。相比之下,有限差分法是基于差分近似代替微分,这种处理方式不一定具备微分方程的性质[33]。因此,有限差分法比有限分析法受到的限制更多(如空间步长);2)有限差分法容易遇到一个难题:在获得稳定数值解时遇到的各种问题通常需要使用人工干预方法来处理,例如使用上游加权格式。为了达到这个目的,在计算格式上需要花费大量精力,从而避免如数值不稳定等问题。然而,这些方法并不是万能的,不能解决所有的问题。从图3i可以看出,有限差分法在入渗初期的边界产生巨大的误差。改进型有限分析法在一定程度上能够规避类似问题;3)与有限差分法相比,有限分析法在相同的网格条件下能够获得更高精度数值解。有限差分法的计算精度主要取决于差分近似代替微分的精度。然而,有限差分近似的精度完全取决于泰勒级数近似中保留的项的数量。
5 结 论
本文推导了能够同时获取空间项与时间项的解析解的有限分析计算格式,以求解Richards方程。分别将改进的有限分析数值模拟结果与解析解、混合型有限分析数值解、有限差分数值解和VSAFT2软件计算结果进行对比,获得以下几个结论:
1)通过与解析解、混合型有限分析数值解和有限差分数值解对比,当选取空间步长等于10 cm时,混合型有限分析法计算精度大大降低且质量平衡误差迅速增加。然而,改进型有限分析法从时间和空间域获取局部解析解,能够获得精度较高的数值解,并且可以较好地控制质量平衡误差,有限差分法数值解的精度较低。
2)通过对比VSAFT2软件计算结果,改进型有限分析法能够用于模拟降雨和蒸发条件下非饱和带水分运移过程。
研究为精确模拟包气带水分运移提供一种可靠方法,丰富了有限分析法的理论,有助于土壤水资源的评价与管理。
[1] Zhang Z Y, Wang W K, Chen L, et al. Finite analytic method for solving the unsaturated flow equation[J]. Vadose Zone Journal, 2015, 14(1): 1-10.
[2] Richards L A. Capillary condition of liquids through porous mediums[J]. Physics, 1931, 1(5): 318-333.
[3] Zhang Z Y, Wang W K, Gong C C, et al. Finite analytic method: Analysis of one-dimensional vertical unsaturated flow in layered soils[J]. Journal of Hydrology, 2021, 597: 125716.
[4] Zha Y Y, Yang J Z, Zeng J C, et al. Review of numerical solution of Richardson-Richards equation for variably saturated flow in soils[J]. Wiley Interdisciplinary Reviews: Water, 2019, 6: e1364.
[5] Celia M A, Bouloutas E T, Zarba R L. A general mass-conservative numerical solution for the unsaturated flow equation[J]. Water Resources Research, 1990, 26(7): 1483-1496.
[6] Haverkamp R, Vauclin M, Touma J, et al. A comparison of numerical simulation models for one-dimensional infiltration[J]. Soil Sci Soc Am J, 1977, 41(2): 285-294.
[7] Milly P C D. A mass-conservative procedure for time-stepping in models of unsaturated flow[J]. Advances in Water Resources, 1985, 8(1): 32-36.
[8] Keita S, Beljadid A, Bourgault Y. Implicit and semi-implicit second-order time stepping methods for the Richards equation[J]. Advances in Water Resources, 2021, 148: 103841.
[9] Sandhu R S, Liu H, Singh K J. Numerical performance of some finite element schemes for analysis of seepage in porous elastic media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1977, 1(2): 177-194.
[10] Ju S H, Kung K J. Mass types, element orders and solution schemes for the Richards equation[J]. Computers & Geosciences, 1997, 23(2): 175-187.
[11] Chen C J, Naseri-Neshat H, Ho K S. Finite-analytic numerical solution of heat transfer in two-dimensional cavity flow[J]. Numerical Heat Transfer, 1981, 4(2): 179-197.
[12] Chen C J, Chen H C. Finite analytic numerical method for unsteady two-dimensional Navier-Stokes equations[J]. Journal of Computational Physics, 1984, 53(2): 209-226.
[13] Hwang J C, Chen C J, Sheikhoslami M, et al. Finite analytic numerical solution for two-dimensional groundwater solute transport[J]. Water Resources Research, 1985, 21(9): 1354-1360.
[14] Wang W K, Dai Z X, Li J T, et al. A hybrid Laplace transform finite analytic method for solving transport problems with large Peclet and Courant numbers[J]. Computers & Geosciences, 2012, 49: 182-189.
[15] 王文科. 用改进的时间差分有限分析法模拟地下水非稳定井流方程[J]. 水科学进展,1996,7(2):112-118.
[16] 王文科. 局部坐标有限分析法及其在腊家滩水源地群孔抽水试验中的应用[J]. 西北地质,1995,28(4):65-71.
[17] Tsai W F, Chen C J, Tien H C. Finite analytic numerical solutions for unsaturated flow with irregular boundaries[J]. Journal of Hydraulic Engineering, 1993, 119(11): 1274-1298.
[18] Tsai W F, Lee T H, Chen C J, et al. Finite analytic model for flow and transport in unsaturated zone[J]. Journal of Engineering Mechanics, 2000, 126(5): 470-479.
[19] Zhang Z Y, Wang W K, Yeh T C J, et al. Finite analytic method based on mixed-form Richards' equation for simulating water flow in vadose zone[J]. Journal of Hydrology, 2016, 537: 146-156.
[20] Zhang Z Y, Wang W K, Gong C C, et al. Finite analytic method for modeling variably saturated flows[J]. Science of the Total Environment, 2018, 621: 1151-1162.
[21] Zeng X J, Li W. The stability and convergence of finite analytic method for unsteady two-dimensional convective transport equations[M]//Chen C J, Chen C D, Holly F M. Turbulence Measurements And Flow Modeling. Washington, D C: Hemisphere Publishing Corporation, 1987: 427-433.
[22] Lin T T, Tseng C M, Yang J C. Fractional steps scheme of finite analytic method for advection-diffusion equation[J]. Journal of Engineering Mechanics, 2005, 131(1): 23-30.
[23] Yeh T C J, Srivastava R, Guzman A, et al. A numerical model for water flow and chemical transport in variably saturated porous media[J]. Groundwater, 1993, 31(4): 634-644.
[24] Gardner W R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J]. Soil Science, 1958, 85(4): 228-232.
[25] Chen H C, Chen C J. The finite analytic method[R]//IIHR Report 232-IV. IOWA: Institute of Hydraulic Research, 1982.
[26] Broadbridge P, White I. Constant rate rainfall infiltration: A versatile nonlinear model: 1. Analytic solution[J]. Water Resources Research, 1988, 24(1): 145-154.
[27] Sander G C. Exact solutions to nonlinear diffusion-convection problems on finite domains[J]. J Austral Math Soc Ser B, 1991, 33: 384-401.
[28] Warrick A W, Lomen D O, Islas A. An analytical solution to Richards' equation for a draining soil profile[J]. Water Resources Research, 1990, 26(2): 253-258.
[29] Srivastava R, Yeh T C J. Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils[J]. Water Resources Research, 1991, 27(5): 753-762.
[30] Romano N, Brunone B, Santini A. Numerical analysis of one-dimensional unsaturated flow in layered soils[J]. Advances in Water Resources, 1998, 21(4): 315-324.
[31] Brunone B, Ferrante M, Romano N, et al. Numerical simulations of one-dimensional infiltration into layered soils with the richards equation using different estimates of the interlayer conductivity[J]. Vadose Zone Journal, 2003, 2(2): 193-200.
[32] 张在勇,王文科,陈立,等. 非饱和带有限分析数值模拟的误差分析[J]. 水科学进展,2016,27(1):70-80.
Zhang Zaiyong, Wang Wenke, Chen Li, et al. Analysis of errors in finite analytic numerical simulation of flow in unsaturated zone[J]. Advances in Water Science, 2016, 27(1): 70-80. (in Chinese with English abstract)
[33] Civan F. Practical finite-analytic method for solving differential equations by compact numerical schemes[J]. Numerical Methods for Partial Differential Equations: An International Journal, 2009, 25(2): 347-379.
Improved finite analytic method to simulate soil water movement in vadose zones
Zhang Zaiyong, Wang Wenke※, Lu Yanwei, Gong Chengcheng, Ran Bin, Wu Zeyu
(1.,,,710054,; 2.,,710054,)
Finite Analytic Method (FAM) has widely been used to solve the Richards equation in recent years. The first-order finite difference approximation can usually be utilized in the hybrid FAM (HFAM) to handle the time derivative term during solution. To some extent, the HFAM can obtain satisfactory results, compared with other numerical methods, such as the modified picard Finite Difference (MPFD) method. However, large errors can also be found using the HFAM to simulate the characteristics of sharp wetting fronts during the infiltration process in the vadose zone. Therefore, a better method is required to handle the time derivative term. In this study, an improved FAM (IFAM) was proposed to accurately simulate the soil water movement in the vadose zone. The IFAM was selected to obtain local analytic solutions from both the time and space domain simultaneously, due mainly to totally different from the HFAM method. Three cases were also considered to systematically evaluate the performance of IFAM. In all cases, the one-dimensional vertical soil columns were set as 100 cm. In the first case, the upper boundary condition was a constant flux boundary, and the lower boundary was a constant pressure head. Three soil columns were discretized into 100, 50, and 10 elements, respectively. The Finite Difference Method (FDM), HFAM,analytic solution, and IFAM were utilized to solve the Richards equation for better comparison. In the second case, both upper and lower boundary conditions were constant pressure heads. The vertical discretization spacing was set as 1 cm. The water movement was then simulated in the vadose zone using IFAM and VSAFT2 (a commonly-used software based on the Finite Element Method (FEM) to solve the Richards equation). In the third case, the upper boundary condition was also assumed to be a flux boundary, and the flux was equal to the amount of evaporation and rainfall. The lower boundary condition was a constant pressure head. The results of the first case showed that the best numerical results was achieved in the IFAM among all numerical methods. Furthermore, the minimum mass balance error was obtained in IFAM even under the condition of larger spatial steps (spatial step equal to 10 cm), compared to the analytical solution. The results from both the second and third cases showed that there was similar solutions to the IFAM in contrast with VSAFT 2. Consequently, the IFAM can widely be expected to significantly improve the numerical accuracy of the solution to the Richards equation under the larger vertical discretization spacing. This finding can also provide a better way for the simulation of water movement in the vadose zone, particularly for sustainable water resources management and ecological protection.
soils; moisture; transport; finite analytic method; vadose zone; numerical simulation
张在勇,王文科,陆彦玮,等. 改进型有限分析法模拟包气带土壤水分运移[J]. 农业工程学报,2021,37(18):55-61.
Zhang Zaiyong, Wang Wenke, Lu Yanwei, et al. Improved finite analytic method to simulate soil water movement in vadose zones[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(18): 55-61. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2021.18.007 http://www.tcsae.org
2020-12-18
2021-05-10
国家重点研发计划子课题(2020YFC1808302-004);国家自然科学基金重点项目(4213000272);国家自然科学基金青年科学基金项目(41902249);陕西省重点研发计划一般项目(2020SF-405);陕西省留学人员科技活动择优资助项目(2020006);中国地质调查局地调项目“塔里木盆地开都河-孔雀河流域源汇项参数体系调查评价”(2021西地委3-08)
张在勇,博士,讲师,研究方向为旱区地下水资源合理开发利用与数值模拟。Email:zaiyongzhang@126.com
王文科,博士,教授,研究方向为旱区地下水文过程与生态效应。Email:wenkew@chd.edu.cn
10.11975/j.issn.1002-6819.2021.18.007
P641
A
1002-6819(2021)-18-0055-07
