高速芯片分选多工位转盘的疲劳寿命预测*
2021-11-23潘小华
周 芸,芦 俊,潘小华
(江苏信息职业技术学院,江苏无锡 214153)
0 引言
转盘式测试分选机是芯片测试环节中重要的设备,以分选效率高、可实现功能多等优点,而逐渐被广泛应用[1]。多工位转盘系统是转盘式芯片分选设备的关键部件,决定着分选设备能否长期稳定地、高效率地工作。本文通过静力学分析方法和Ansys有限元软件疲劳分析工具,分析多工位转盘系统在持续间歇式高速启停转动下的工作应力,预测其抗疲劳强度能否满足芯片分选设备长期稳定、高速运行的工作寿命要求。
1 多工位转盘工况分析
1.1 工作节拍
分选设备的多工位转盘系统由转盘和吸笔组件等组成,转盘分为转盘本体和转盘支撑臂两部分,如图1所示。转盘本体与直驱旋转电机联结,吸笔组件安装于转盘支撑臂顶端,吸笔可上下滑动。整个转盘等分成20个工位,每两个工位之间的夹角是18°,分选设备的分选效率要求是每小时分选产量(UPH)不低于36 000颗。转盘每转动一个分度,可完成一颗芯片的分选。
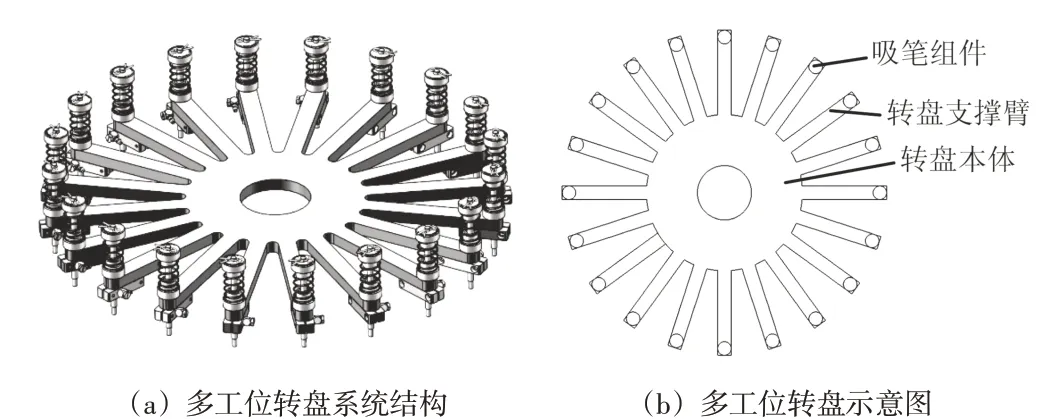
图1 多工位转盘系统
工作节拍如图2所示,t1为转盘转动一个分度时间;t2为转盘到位整定时间;t3为吸笔下降时间;t4为吸笔工作时间;t5为吸笔上升时间。在t1时间内,转盘转动一个分度。根据分选效率的要求,在t3、t4和t5时间一定的情况下,t1和t2时间越短,即转盘转动越快,分选效率就会越高。依据图中转盘系统的工作节拍,在t1时间开始时刻,转盘高速启动,在t1时间结束时刻,转盘立即停止,在t2、t3、t4、t5时间后,转盘再次启动,由此可知转盘是做间歇式的高速转动。

图2 多工位转盘系统工作节拍
1.2 转盘动载荷分析
转盘与直驱旋转电机(Direct Drive Rotate Motor)直接刚性耦合,直驱电机驱动转盘做高速间歇性旋转运动,从而在转盘上产生周期性的动载荷。动载荷来源于两个方向,一个是沿转盘径向,由角速度产生的离心力;一个是沿转盘切向,由于转盘的急加速和急减速而产生的惯性力矩。
对于转盘支撑臂而言,转盘每转一个分度,就承受一次这样的交变载荷。按照分选效率要求,每小时转盘需要转动36 000个分度。按一天工作20 h计算,一天就要转动7.2×105个分度。按设备工作寿命10年计算,理论上转盘支撑臂要能承受2.6×109次的疲劳载荷。
根据疲劳理论,金属材料的疲劳裂纹起源于高应力区,而高应力区发生在材料表面的几何突变处,几何突变处的应力集中削弱了材料局部的疲劳抵抗能力,从而吸引疲劳裂纹在这里形核[2]。因此对高速启停转动下的转盘疲劳强度分析,主要就是针对转盘支撑臂与转盘本体之间连接处的疲劳强度分析,这是个高周疲劳。
根据分选效率要求推算,一次工作周期要求节拍时间t1+t2+t3+t4+t5≤0.10 s,设计转盘旋转一个分度时间t1≤0.050 s。因为直驱电机转一个分度的时间t1非常短暂,所以对t1时间内的转盘高速启停,选择大加速和大减速的三角形加减速曲线,即:
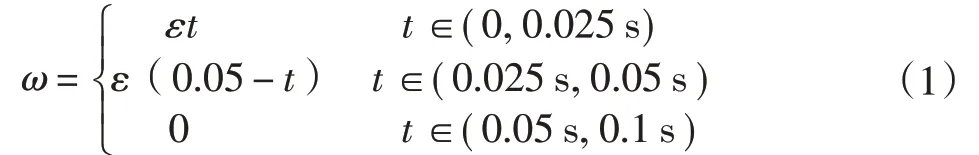
式中:ω为转盘角速度;ε为转盘角加速度。
按照t1=0.05 s,转盘转动18°,根据式(1)可计算出转盘角加速度ε=502.4rad/s2。(0,0.025s)时间内转盘加速, (0.025 s,0.05s)时间内转盘减速,(0.05s,0.1s)时间内转盘处于停歇期。
(1)转盘离心力动载荷
转盘支撑臂及其顶端吸笔组件产生的离心力FN:
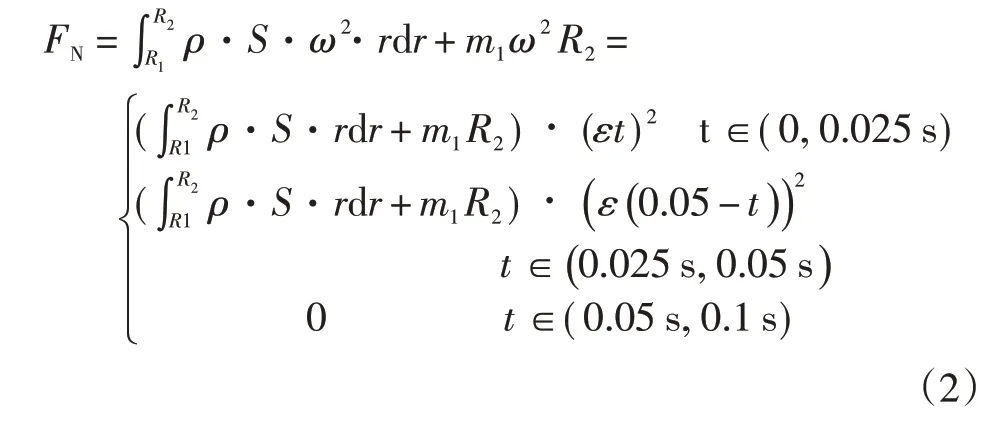
式中:R1为转盘支撑臂根部到转盘中心距离;R2为转盘支撑臂顶端到中心距离;S为转盘支撑臂横截面面积;r为转盘支撑臂上某一点到中心距离;m1为吸笔组件质量;ω为转盘角速度;ρ为转盘支撑臂密度。
当转盘速度达到最大时,即转盘加速阶段停止时刻t=0.025 s时,此时的离心力FN达到最大离心力FNmax。最大离心力FNmax对转盘支撑臂与转盘本体之间的连接截面产生最大拉伸应力σNmax:

支撑臂上所受的拉伸应力是脉动循环应力,如图3所示,T1为加速时间,T2为减速时间,T3为转盘停歇时间。
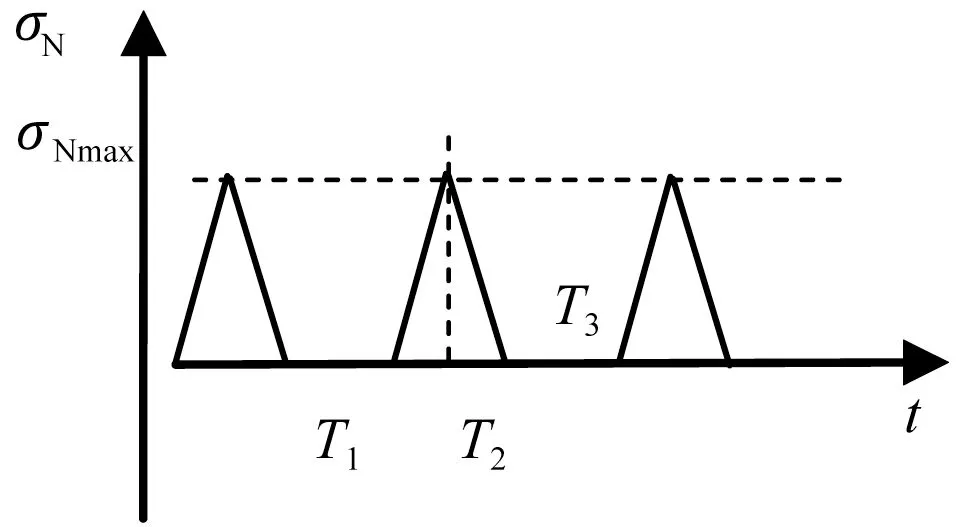
图3 支撑臂上脉动循环拉伸应力σN
(2)转盘惯性弯矩动载荷
转盘支撑臂及其顶端吸笔在转盘加减速阶段,产生惯性弯矩M。由于启停加速度恒定,对应的惯性弯矩即为最大弯矩Mmax:
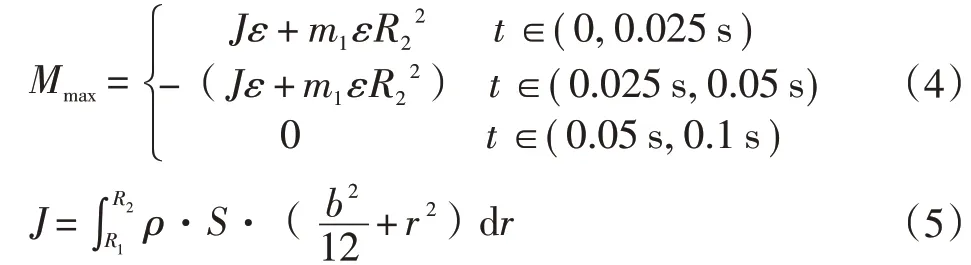
式中:J为转盘支撑臂对转盘中心的转动惯量;b为支撑臂的宽度。
由式(4)可知,当转盘高速间歇式转动时,转盘支撑臂在加速阶段与减速阶段产生的惯性弯矩幅值相等,方向相反。在转盘支撑臂上产生交变循环的弯曲应力σr,在转盘本体与转盘支撑臂之间连接截面处离中性轴最远处产生最大的交变循环弯曲应力σrmax,如图4所示。

图4 支撑臂上交变循环弯曲应力σr

1.3 组合应力分析
综合上面分析,转盘高速间歇式转动时,转盘支撑臂的变形是轴向拉伸与弯曲的组合变形,臂上的应力是由拉伸应力和弯曲应力组合而成,最大拉应力和最大压应力发生在弯矩最大的横截面,即支撑臂与转盘本体连接截面上离中性轴最远的上边缘与下边缘处[3],结合式(3)与式(6),最大拉应力σ∑max和最大压应力-σ∑max如下所示:

符号说明同上。
1.4 转盘动载荷计算
根据针对的求解对象,考虑主要因素,对转盘系统做适当简化,把吸笔组件等效为集中质量块。由于转盘是做高速的间歇式启停转动,所以尽可能要求转动惯量小,转盘材料采用铝合金材质。支撑臂弹性模量弹性系数E=68.9 GPa,密度ρ=2 710 kg/m3,泊松比ν=0.35,吸笔组件质量为36.52 g。基于尽量最小化负载转动惯量的考虑,各部分尺寸在满足工作和基本装配要求下,结构尽量紧凑。据此设计转盘支撑臂根部到转盘中心距离R1=60 mm,支撑臂顶端到转盘中心距离R2=155 mm,支撑臂宽度b=12 mm,厚度h=8 mm。启停加速度ε=502.4rad/s2。
由以上设计参数,结合式(2)~(6),计算得到最大离心力FNmax=1.312 1 N,对应产生的最大拉伸应力σNmax=13.667 8 kPa;加减速阶段的恒定惯性弯矩幅值Mmax=0.597 1 N·m,对应产生的最大弯曲应力σrmax=3.110 2 MPa。比较σrmax和σNmax,σrmax远大于σNmax,结合式(7),可知转盘支撑臂最大拉应力主要由惯性弯矩产生,因此后面主要针对惯性弯矩下的转盘疲劳强度进行分析。
2 疲劳强度计算与分析
2.1 疲劳极限影响系数
疲劳极限影响系数k:

式中:Kf为疲劳缺口系数;εσ为尺寸修正系数;β为表面质量系数。
疲劳缺口系数Kf与弹性应力集中系数Kt有关,两者之间的关系可以表示为[2]:

式中:q为疲劳缺口敏感系数。
根据Neuber公式[2],有:

根据设计手册,转盘支撑臂之间的缺口应力集中系数Kt=1.8[4]。r为缺口半径,转盘支撑臂根部的缺口半径r=4 mm;a与材料有关的特征长度,对于极限强度为310 MPa的铝合金材料,a=0.6。
结 合 式(9)~(10),计 算 得:q=0.720 8,Kf=1.5767。
尺寸修正系数参考经验公式[2],取εσ=0.93;转盘采用精加工方式,表面质量系数取β=0.95。综合上述3种因素,不考虑表面处理的影响下,支撑臂在对称循环弯曲交变应力下的疲劳极限影响系数:

2.2 S-N曲线
取出Ansys有限元软件中,铝合金材料在应力比Ratio=-1的交变循环载荷下的S-N曲线疲劳极限数据,如图5所示。该曲线是没有应力集中的光滑标准件疲劳极限曲线。根据2.1节中计算的疲劳极限影响系数k=0.560 3,对S-N曲线进行修正[5],修正后的对应于转盘支撑臂的S-N曲线疲劳极限数据,如表1所示,修正前后的S-N曲线如图6所示。

图5 光滑标准件疲劳极限强度与循环次数关系

图6 Ratio=-1的修正前后的S-N曲线

表1 支撑臂疲劳极限强度与循环次数关系
2.3 理论疲劳强度分析
由表2可知,当修正后的交变循环应力σ-1r=4.636×107MPa时,循环次数达到1×108次。由前述1.4节,对于转盘支撑臂,其在等幅循环弯矩载荷下的应力幅σrmax=3.110 3 MPa,结合表1的疲劳极限强度,得到安全因子n1=14.905。
安全因子14.91大于1很多,因此理论上转盘支撑臂的疲劳强度可以满足分选设备长时间的高速间歇式运行。
2.4 基于Ansys的疲劳强度分析
2.4.1 边界条件
在Ansys Workbench软件的静力结构(Static Structural)分析中,设置转盘最内侧圆环面为Fixed-Support约束,即固定住转盘内圆面。在转盘的几何中心建立直角坐标系,Z轴垂直于转盘面,Y轴沿支撑臂伸展方向[6-7]。
2.4.2 载荷施加
添加1.4中计算得到的幅值为0.597 1 N·m的力矩载荷,作用于支撑臂侧面上;施加重力加速度(Standard Earth Gravity),方向垂直于转盘面向下。
2.4.3 结构静力分析
在静力结构分析的Solution中,设置应力选项为Normal Stress,方向沿Y轴。在求解计算后,得到支撑臂上沿Y向的最大正应力Normal Stress=3.357 6 MPa,如图7所示。与前面理论计算得到的最大拉伸应力3.110 2 MPa,相差约7%,这主要是由于计算模型细节上的差异造成的。

图7 支撑臂Y向最大正应力(Normal stress)云图
2.4.4 支撑臂疲劳分析
在静力结构分析中,添加疲劳分析工具Fatigue Tool,根据2.2中的计算,设置疲劳强度影响因子Fatigue Stress Factor为0.56;载荷类型R=-1,表示对称循环载荷;分析类型Analysis Type设为Stress life应力寿命;在比例加载下,对铝合金这类宏观各向同性的韧性金属材料,采用形状改变比能理论来校核其疲劳破坏,因此在Stress Component选项中选择Von Mises等效应力。
经过有限元计算后得到等效交变应力云图、双轴指示云图、疲劳安全因子云图,分别如图8~10所示。由图8可知,基于Von Mises等效应力得到的最大等效交变应力为6.408 2 MPa。
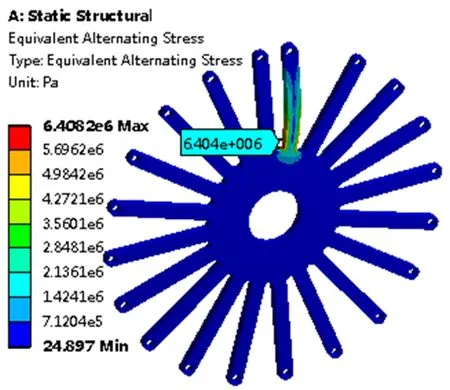
图8 支撑臂等效交变应力云图
通过支撑臂双轴指示云图(biaxiality indication)(图9)来查看支撑臂根部的局部应力状态,可看到支撑臂根部的双轴指示B值接近于0,这表明支撑臂根部的应力属于单轴应力主导的区域。而S-N疲劳试验曲线是光滑标准件在单轴应力作用下测定的,反映的是光滑标准件的单轴应力状态,所以支撑臂根部区域的应力状态与光滑标准件试验条件下的应力状态相似。
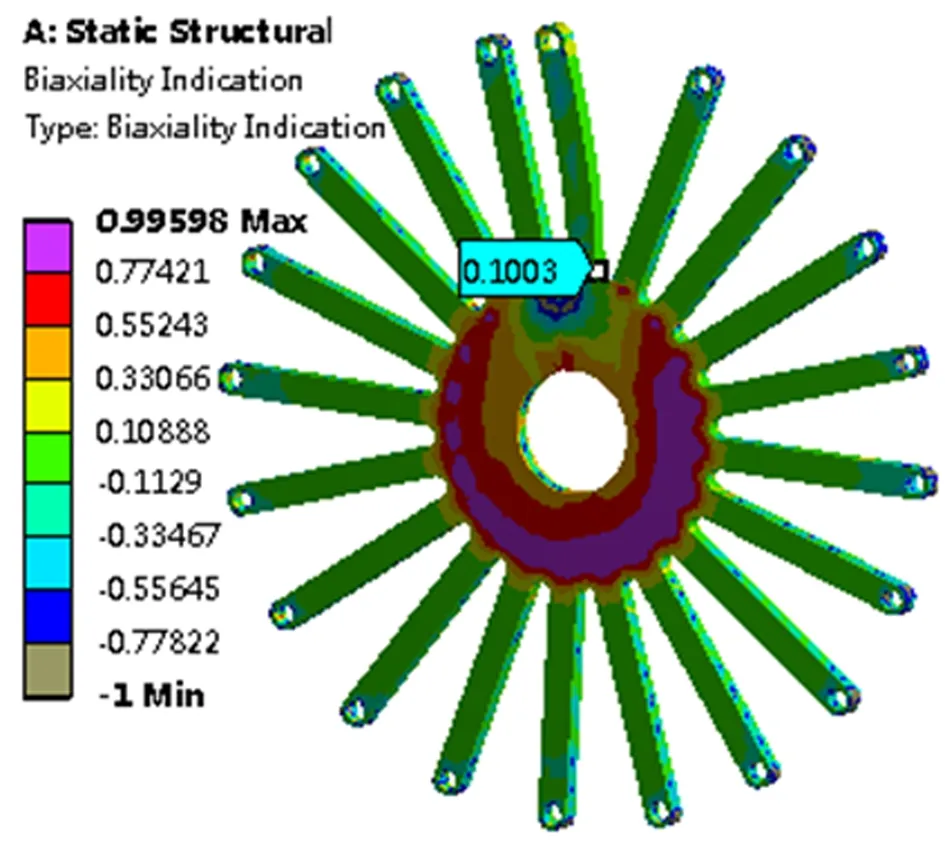
图9 支撑臂双轴指示云图
2.4.5 安全因子

式中:σ-1为S-N曲线上循环次数达到1×108时所对应的极限疲劳强度;σf为工件的实际工作应力。
由图8中的最大等效交变应力和图5中的疲劳极限强度,计算得n2=12.911 6。
由计算得到的安全因子n2与支撑臂疲劳安全因子云图(图10)中的最小Safetyfactor=12.912基本相同。
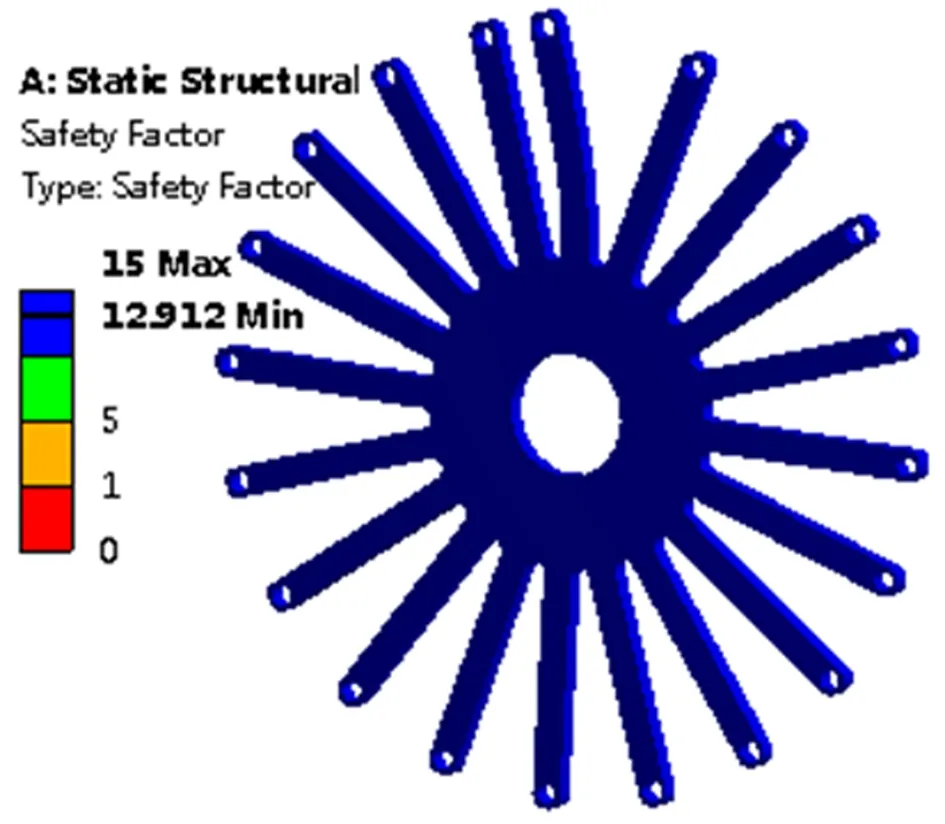
图10 支撑臂疲劳安全因子云图
安全因子n1、n2都超过1的10倍以上,表明支撑臂所受的实际工作应力远小于材料的极限疲劳强度。按抗疲劳断裂计算许用安全系数N=N1N2N3[8],取N1(转盘材料可靠性)=1.1,N2(转盘重要性)=1.3,N3(计算精确性)=1.3,计算得许用安全系数N=1.86。安全因子n1、n2都大大超过了许用安全系数N,因此转盘支撑臂在芯片分选设备的这种工况下,疲劳极限循环次数将达到108次以上。考虑到安全因子的余量很大,同时理论上认为对有色金属材料,疲劳极限循环次数超过108次时,可认定工件具有无限疲劳寿命[2],因此可以认为转盘支撑臂可达到2.6×109次的循环寿命。
3 电机驱动能力
通过计算得到转盘系统(含吸笔组件)的转动惯量为0.025 3 kg·m2,本文选用的某公司ATR152-138型号直驱型旋转电机峰值扭矩为53.5 N·m,连续扭矩为17.8 N·m,扭矩常数为5.15(N·m)/A,转子惯量为0.001 587 kg·m2[9]。按式(1)中50 ms内的转盘角速度加减速曲线,转盘停歇时间50 ms,安全系数为30%,以便将摩擦力和外界应力抵消为0,计算转盘系统所需的最大驱动力矩和均方根(RMS)力矩[10]分别为:
最大驱动力矩:Td=17.560 4 N·m
均方根(RMS)力矩:

由式计算可知,通过计算得到驱动转盘系统的峰值扭矩和均方根(RMS)力矩,分别小于直驱电机的峰值扭矩53.5 N·m和连续扭矩17.8 N·m,所以所选的电机驱动能力足够,可以驱动此转盘系统。
4 结束语
转盘式芯片分选设备中的高速转盘在间歇式高速启停转动下,引发交变的惯性力,从而在转盘支撑臂产生交变循环应力,转盘支撑臂根部是最容易发生疲劳破坏的地方。本文通过静力学分析方法和Ansys有限元软件疲劳分析工具,分别计算了转盘支撑臂所承受的交变应力,进而计算和分析了转盘支撑臂的疲劳极限安全因子。通过分析表明,转盘支撑臂可以达到2.6×109次的疲劳循环寿命,同时计算出的疲劳极限安全因子还有比较多的余量,后期还可以增加转盘启停转速,提高转盘工作节拍,提升芯片分选设备的分选效率。
