基于能耗预测的空调测试任务调度问题研究*

张 恪，赖信君，黎展滔※，林深和，陈庆新，毛 宁，李 鑫

（1.广东工业大学机电工程学院，广州 510006；2.珠海城建智慧能源有限公司，广东珠海 519070）

0 引言

全球能源消耗与碳排放总量逐年增长，严重威胁着人类社会的可持续发展。中国是一个空调生产大国，焓差实验是空调性能测试和能效标定的主要手段，其通过冷热平衡来达到实验室内空气高精度的温度和湿度，因此试验过程需要消耗大量的电力。以江苏省某亚太地区空调测试企业龙头为例，其每年的测试任务耗电量为1.9亿kW·h，按当地电价，耗电费用高达1.95亿元，具有极大的能耗优化空间。

通过调研发现，大部分进行焓差实验的空调测试企业没有充分利用分时电价政策实现电费成本优化。焓差实验的准备（“打工况”）时间及能耗难以确定，是其中主要的原因；此外，测试任务顺序的改变，也会对测试任务“打工况”的时间及能耗产生较大影响。这也是大量高能耗企业在生产调度过程中，因准备时间及能耗不确定且具有任务顺序相关性，而难以充分利用分时电价实现成本优化的原因。

国内外文献有较多关于分时电价下的任务调度研究，耿凯峰等[1]针对多目标绿色可重入混合流水车间调度问题的特点，在机器分配和工序排序的基础上引入分时电价机制，构建了以最小化最大完工时间、总能耗成本和碳排放为目标的绿色调度优化模型，提出了一种改进的多目标文化基因算法来求解该问题；Ding JY[2]、Che A[3]研究了在使用分时段电价计划和无关并行机器调度问题背景下，均改进了基于连续时间间隔的混合整数线性规划公式并分别提出了一种列生成启发式算法和一种两阶段的启发式方法。目前，分时电价调度问题中机器设置时间一般会默认设置为服从某种特定分布进行求解，而本文中测试任务“打工况”时间与耗电率的变化很难用特定的分布函数去描述，需要收集多种传感器数据及数据预测手段进行解决。其中，选择一种合适的预测算法是其中的关键。丁飞鸿等[4]和闫军威等[5]研究显示，集成学习方法如随机森林、xgboost等算法通过集成多个弱学习器，能以较低的计算开销显著提高模型的预测能力，适合应用于本研究。

任务调度问题是经典的NP-Hard问题，目前求解方法主要有精确算法和启发式算法等。其中精确算法经常使用混合整数规划（Mixed Integer Programming，MIP）模型、分枝定界[6]等方法对问题求最优解，但求解过程耗时较长，且随着问题规模扩大求解时间和难度也进一步增强，而遗传算法（Genetic Algorithm，GA）作为一种群智能优化的启发式算法[7]，在高原等[8]最近研究中显示，其在收敛性、鲁棒性、通用性和扩展性等方面都具有优异的表现，被广泛应用于在组合优化问题求解过程之中。其中，李书全等[9]研究显示传统的交叉算子如PMX、OX等算子重组是随机的，不能够大概率地生成优于父代的子代个体，搜索速度较慢，故本文采用Inver-over算子通过倒置操作可以有效的引导交叉子代大概率向最优解的方向进化，适合应用于本研究。

如何有效地运用数据预测方法解决数学规划中参数（其变化曲线不能用常规分布描述）不确定性问题，是近年来的热点。较多的研究及应用大多把预测及优化设置为两个单独模块，如王犇[10]和井华等[11]首先对需求及环境变量进行预测，再进行任务调度；刘民等[12-13]在求解大规模复杂色织生产调度问题时，首先对整经轴数进行预测，继而作为优化模型的输入。其求解思路均为先完成预测，再进行优化，两个阶段之间较少关联。而在本问题中，若采用GA算法对调度问题进行求解，假设每一条染色体代表一种任务顺序，则不同的序列将对任务的打工况时间及能耗产生影响，这导致GA在迭代过程中需要对任务打工况时间进行多次预测。该情况在已有文献中较少讨论，如何实现机器学习算法与GA算法的有机结合，是本研究的难点。

基于以上综述：第一，本文通过引入机器学习算法，实现分时电价政策下更精细化的任务调度问题分析。第二，提出一种RF-GA混合算法求解思路，适用于分析因任务顺序改变而产生的准备时间及能耗未知的问题。区别于以往数据挖掘及数学规划结合中往往两个模块相互独立的情况，本研究进一步探索两种方法的深度及有机结合，以获得更贴近实际、更可行的方案。第三，根据本文特点，挑选一种合适的编码方式及交叉算子应用到GA算法中。最后，通过实验及实际应用检验所提出RF-GA混合算法求解思路的实用性及优越性。

1 分时电价调度模型

如图1所示，该问题可以描述为：有N个空调的测试任务在J个相互独立的实验台进行测试，其中每个任务集的特征包括1个安装任务、S个测试任务以及每个任务相对应的时长及耗电率；每个测试任务又分为实验台“打工况”和空调测试两部分；其中空调测试时间有相关工艺要求，“打工况”时间主要依赖于上一次测试任务的环境温度/湿度与当前测试任务环境温度/湿度差值。

图1 问题描述

本文中电价遵循分时段定价方案，即该企业所在城市的电价会在一天内进行变化。在分时段电价方案中，时间范围分为K个时段，其中每个时段的电价为Ck。

本文的目标为将I个任务分配到J个相互独立的实验台的可用时段进行测试，在保证任务不拖期的情况下，最大程度的降低实验台电费。

在对实验台和测试任务进行分配时需严格遵循该企业实际情况：（1）实验台数量、任务集数量及测试任务数量已知且确定；（2）每个实验台同一时刻一次只能进行一项测试任务；（3）每个实验台具备测试所有任务的能力；（4）每项测试任务的测试要求已知且确定；（5）测试任务一旦开始，不能半途停止；（6）测试开始时就可以使用所有实验台及进行所有测试任务。基于以上条件，构建关于测试任务的分时电价模型，其相关符号、变量如表1所示。

表1 模型参数符号及其说明

具体数学模型如下：

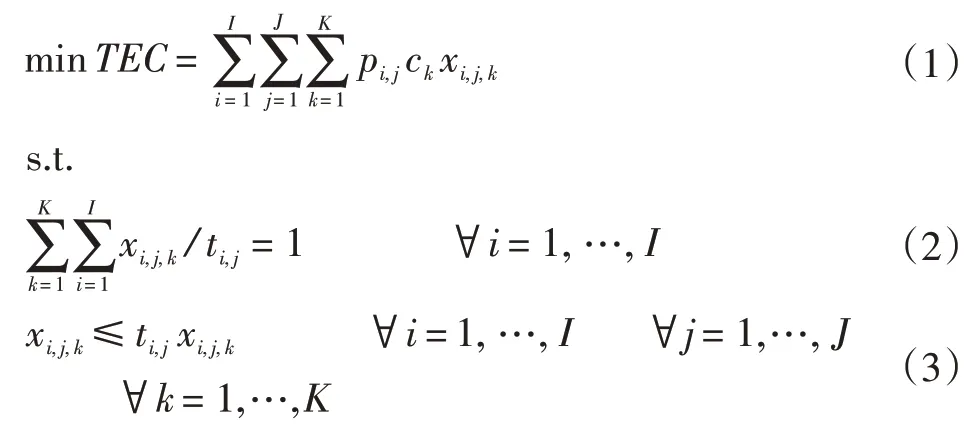
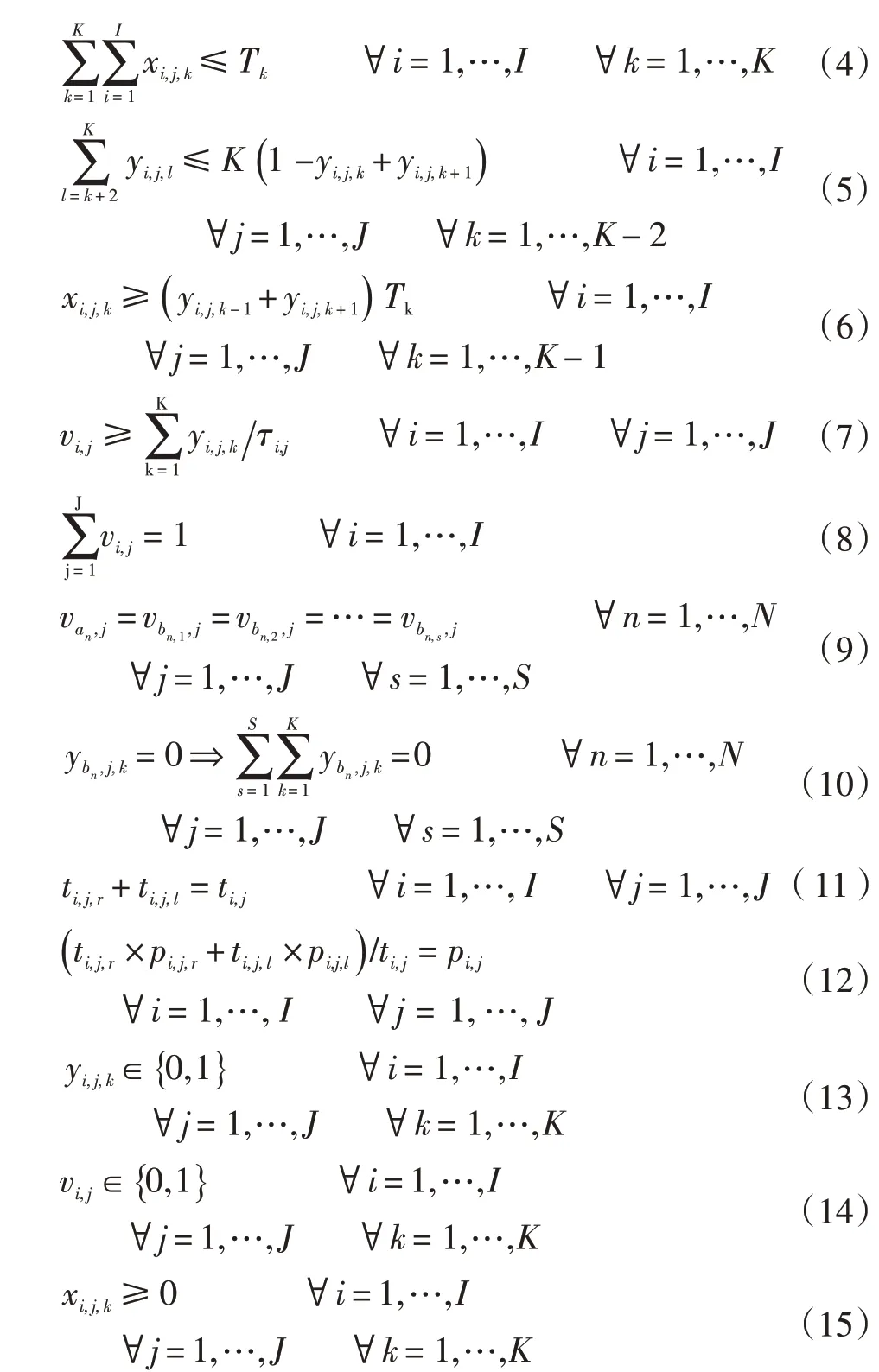
其中，式（1）为目标函数表示在任务不拖期的情况下使得实验台耗电费用最低；式（2）为任务分配到实验台j上的各个时段时长之和等于分配到实验台j上的任务时长；式（3）为任务分配到实验台j上时段k的时长小于等于分配到实验台j上的任务时长；式（4）确保任务分配到实验台j上时段k的所有任务时长之和一定小于该时段的时长；式（5）～（6）保证任务连续完成不会中断；式（7）确保任务跨越电价的最大时段数与该任务分配到实验台j的不同电价时段k的和相等；式（8）保证每个任务只能分给一个实验台；式（9）保证组装任务与测试任务均在相同实验台上进行；式（10）为组装任务结束后才可以进行测试任务；式（11）～（12）为实验台进行一次完整实验与分别进行打工况、测试任务参数之间的等式约束；式（13）～（15）为决策变量的取值约束。

2 RF-GA混合算法求解思路

本文中实验台及测试任务调度问题具有较高的复杂性，需要考虑分时段电价特点和各项测试任务“打工况”时间和耗电率未知且随测试顺序变化的情况。根据此情况，如果采用先预测再进行优化的传统方法，则需要预测出全部测试顺序下任务“打工况”时间和耗电率，不仅增大任务计算量还使得问题变的更加复杂。因此，如图2所示，针对该问题，本文提出一种RF-GA混合算法求解思路，该求解思路主要分为两个模块，即数据预测模块和算法求解模块。两模块之间不是简单的独立关系，而是数学优化方法与数据挖掘技术深度结合：调度模型中任务“打工况”时间与耗电率为未知量，需要利用机器学习算法对其进行预测；而模型的输出结果为测试任务顺序，其决定了当前测试任务开始前的测试环境所处状态，即预测模型的输入变量，于是在算法每一次迭代过程中，RF算法与GA算法采用并行处理方式对任务测试顺序进行求解，提高了模型的求解效率。

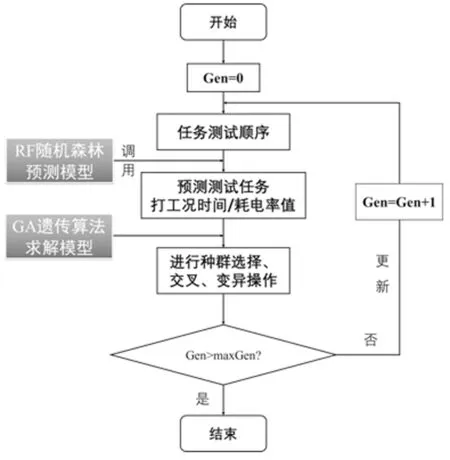
图2 RF-GA混合算法求解思路

2.1 随机森林预测模型构建

随机森林RF（Random Forest）算法是一种基于决策树的集成学习算法，通过对分类回归树CART（Classification and Regression Tree）的集成来提高预测精度，是一种著名的集成学习算法[14-15]。本文采用随机森林回归RFR（Random Forest Regressor）方法对测试任务打工况时间和耗电率进行预测，RFR是RF理论的重要应用，即取所有决策树的预测均值作为预测结果。在实际应用中，需要结合企业实际传感数据对模型进行训练。

随机森林回归模型构建过程如下所示：（1）利用Bootstrap抽样从测试任务“打工况”时间/耗电率历史数据集中抽取z个训练样本集；（2）构建决策树时，随机抽取一定数量的候选属性，从中选择最合适属性作为分裂节点；（3）设定树的棵数ntree值，作为决策树生长的终止条件；（4）生成的z≤ntree棵决策树组成随机森林回归模型，将每一棵决策树输出的均值作为最终预测结果。

2.2 遗传算法编码设计

有效的编码可以在不产生非法解的情况下能表达出个体与可行解的关系。本文问题包含2个子问题：实验台分配和任务集任务排序。因此，本文采用两段式编码方式，将2个子问题编码到一条染色体上，用来表示本问题的一个可行解[16]。假设有4台被测空调（A～D）在2个实验台进行测试，4个空调的测试任务数量分别为8、8、6、7，染色体编码方式如图3所示。实验台分配的编码方式为插入式编码，4个任务集随机排序后在中间任意位置插入一个字符E即可将4个任务集分配到2个实验台上。每一个任务集代表一台被测空调，根据实际情况，每台被测空调分配到相应实验台后不可进行更换，只能在当前实验台完成全部测试任务，所以任务集之间采取分段编码，测试任务编码采用整数编码，每一个测试任务代表一个数字。如任务集1中包含8个测试任务，将该基因片段编码为1～8的数字组合。

图3 染色体的编码方式

2.3 交叉操作

本文采用一种Inver-over算子，该算子运用倒置操作不仅可以使生成的新基因片段中各基因之间相对顺序保持不变——即染色体上的重要基因更加紧凑，更不容易被分裂；还可以使那些在父代中离得很远的基因位在后代中紧靠在一起，提高了算法的种群多样性和全局搜索能力。

该算子较好地利用了种群中获得的信息来指引个体进行交叉操作使交叉子代大概率向最优解的方向进化，其具体步骤如下：（1）设定一个交叉概率λ，在父代染色体A中随机选择一个起始点，比如起始点值为2；（2）产生一个0～1的随机小数，若小于λ，则在刚才选中父代染色体A中随机选择另一个终止位置点，比如终止位置点的值为7，然后将起始点与终止点位置之间的部分倒置（不包括起始与终止位置）；（3）产生一个0～1的随机小数，若大于λ，则从种群中任意在选择一条父代染色体B，找到父代A中起始点值所在的位置，即父代染色体B中值为2的位置在首位，然后选择其下一个位置的值等于7，返回到父代A找到值为7所在的位置，即父代A倒数第二位作为终止点，将父代A起始点与终止点之间的部分倒置（不包括起始与终止位置）；具体过程如图4所示。

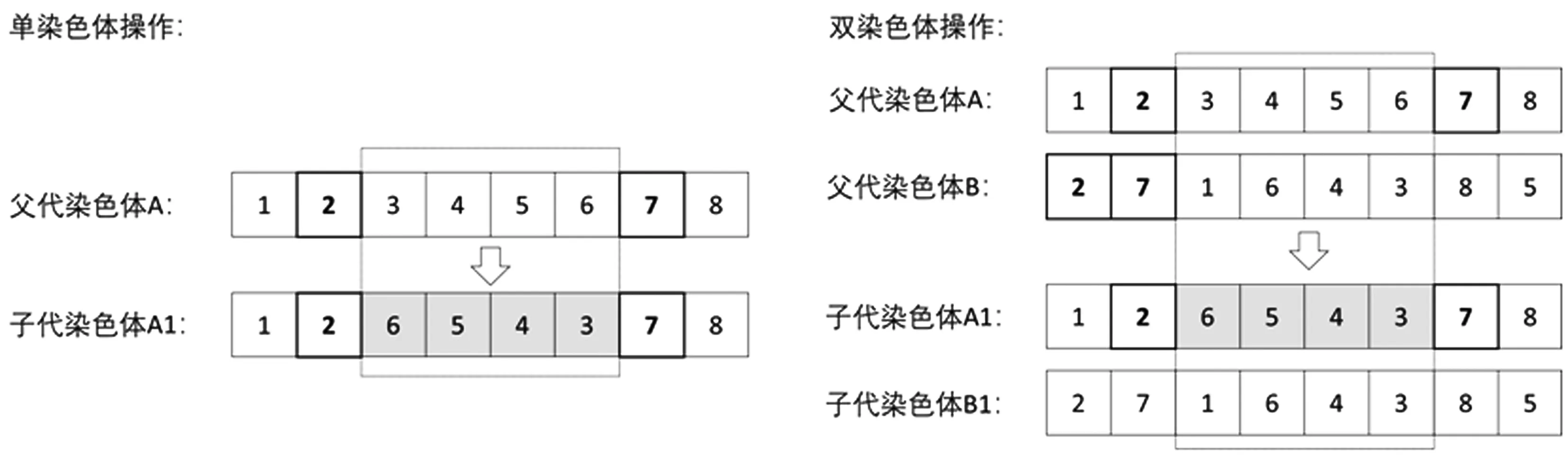
图4 Inver-over算子操作

2.4 变异操作

本文采用两点互换变异操作，在相应部分任意选择两个互换点，然后互换对应位置的编码，此变异操作方法可以保证编码的合法性。具体过程如图5所示。

图5 变异操作

3 实验及分析

3.1 预测结果对比

由江苏某大型空调测试实验中心提供的5 600多条具有代表性的实际空调测试数据对模型进行训练。该企业对实验台内部布置了多种传感设备，共能收集约26种数据。对数据进行清洗、探索性、相关性及显著性分析后，结合预测任务及企业实际业务可行性分析后，最终得到一个9维的输入自变量，分别为“打工况”前内干球温度r1、“打工况”前内湿球温度r2、“打工况”前外干球温度r3、“打工况”前外湿球温度r4、测试内干球温度r5、测试内湿球温度r6、测试外干球温度r7、测试外湿球温度r8、实验台制冷量r9。

为了对照分析证明随机森林预测模型性能的优良性，本文采用了多元线性回归（Multiple Linear Regression，MLR）、MLP深层感知机、支持向量机回归（Support Vector Regression，SVR）和贝叶斯岭回归（Bayes Ridge Regression，BRR）模型对相同样本数据进行了分析和研究，将均方误差（Mean Square Error，MSE）和平均绝对误差（Mean Absolute Error，MAE）作为评估标准。

比较结果如表2所示，RFR算法在预测打工况时间和实验台耗电率两项的MSE、MAE值最小要远优于其他机器学习算法，且耗时较短，能够很好的满足模型在迭代求解过程中对于预测模型的在运算时间和预测精度两方面的要求，适合与GA算法进行深度结合。

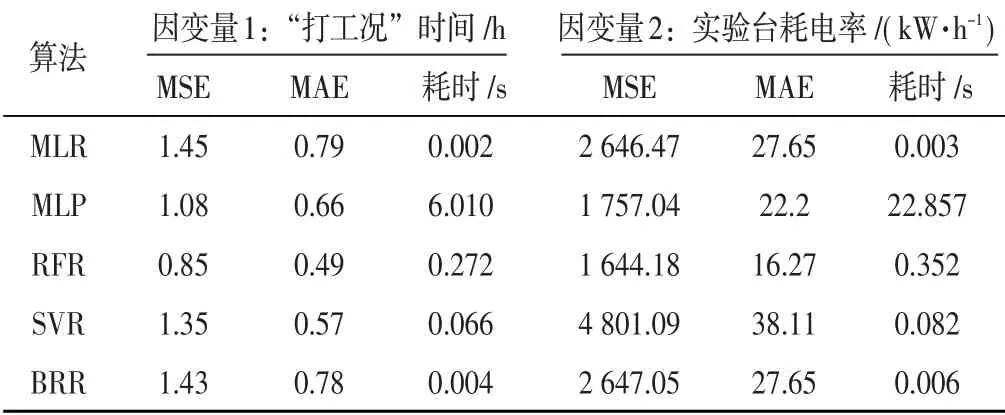
表2 不同数据预测算法预测结果对比

3.2 测试算例与实验环境设定

为了测试本文所提出Inver-over算子性能的优良性，以该实验中心日常测试数据为基础，分析提取其所具备的特征，引入DURASEVIC[17]实验设计的思想，随机生成72组具有该实验中心实际测试案例特征的测试算例，算例命名格式为α-β-γ-ε-δ。其中参数α为实验台数量，参数β为任务集数量，参数γ为测试集任务数量，二者共同决定测试规模大小，参数ε和δ分别代表测试集任务中最大温度/湿度差，可以用来体现温度变化范围大小，算例实验详细参数如表3所示。

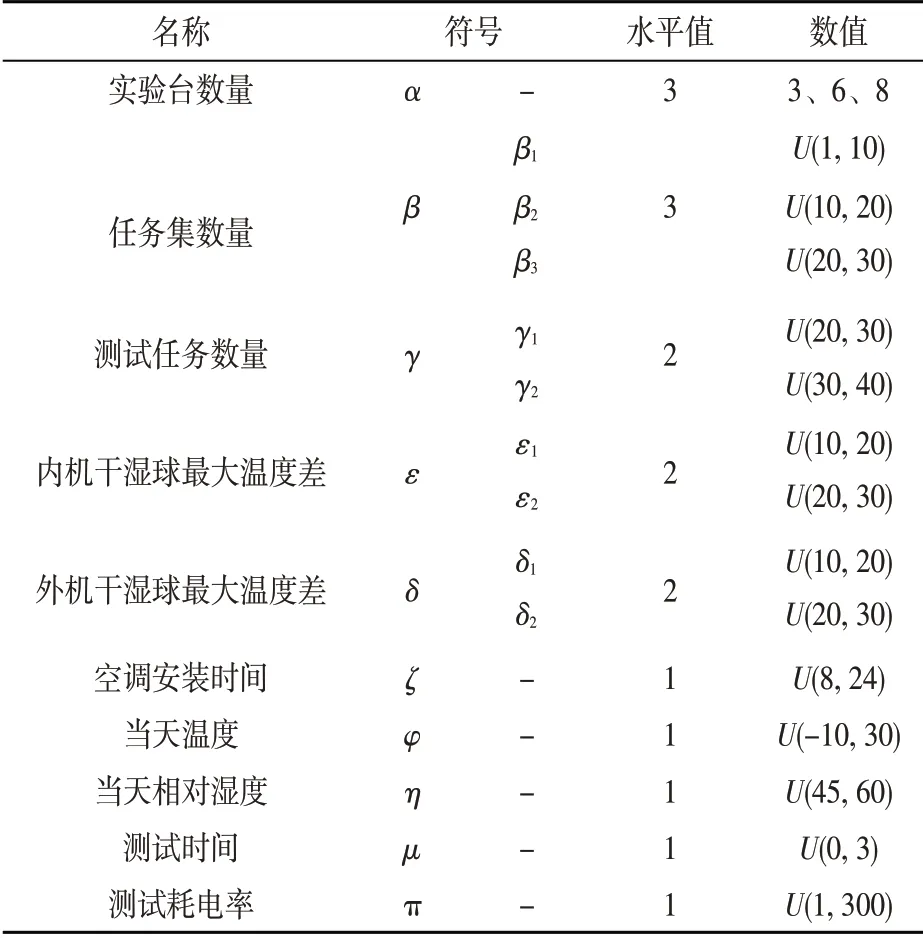
表3 测试算例参数表

在英特尔酷睿i7处理器及Windows10系统下，算法采用Matlab R2016b编程实现。

3.3 各种算法性能比较

为了验证本文所提出Inver-over算子性能的优良性，实验中将以SA算法、6种采用常规交叉算子操作的GA算法作为比较对象。其中GA算法种群选择操作采用轮盘赌[18]方法，其他参数设置如下：种群大小为100，代沟为0.8，遗传算法交叉率λ＝0.8，变异率θ＝0.05；其他算法中SA初始温度100，冷却系数0.99。所有算法皆随机初始化初始种群，为了保证公平起见且满足企业实际需求，这里以迭代次数作为算法的终止条件。当β=3且γ＝2时，将任务规模定义为大规模测试算例，迭代终止次数为500次，其余实验迭代次数为300次。8种算法将在每个算例组合下分别进行5次独立实验，将实验台总耗电费用求均值，作为算法评估的观察指标。表4所示为8种算法在各个算例组合下的测试结果，测试结果中每种算法的性能分布与该实验中心实际测试案例进行计算得到的性能分布类似，说明运用该方法生成的随机测试数据具有一定的可用性。由表4可得如下结论。

表4 不同算法实验统计结果

（1）应用遗传算法求解该企业问题的结果要优于使用模拟退火算法；而对于同样应用遗传算法求解时，使用不同遗传算法在不同性质的测试环境下求解性能也不尽相同。总体来看，本文所应用的Inver-over算子在大部分测试环境下具有良好的求解性能；循环交叉算子（Cycle Crossover，CX）和部分匹配交叉算子（Partially-matched crossover，PMX）在少部分测试环境下具有良好的求解性能；而应用其他交叉算子的遗传算法只在极少数特定环境下的结果较优，总体而言优化效果较差。

（2）由图6可知，在测试任务集数量小的时候，Inver-over算子、PMX、OX算子等能够在基因片段长度较短的情况下对基因进行较大程度重组的算法相对于其它算法的算例最优次数较多；而随着测试任务集数量增加，Inver-over算子在性能上出现一定劣化但是劣化趋势较为缓和；而CX算子随着基因片段长度增加，染色体片段大幅度改变的机会增加，于是在性能上实现了较大飞跃。

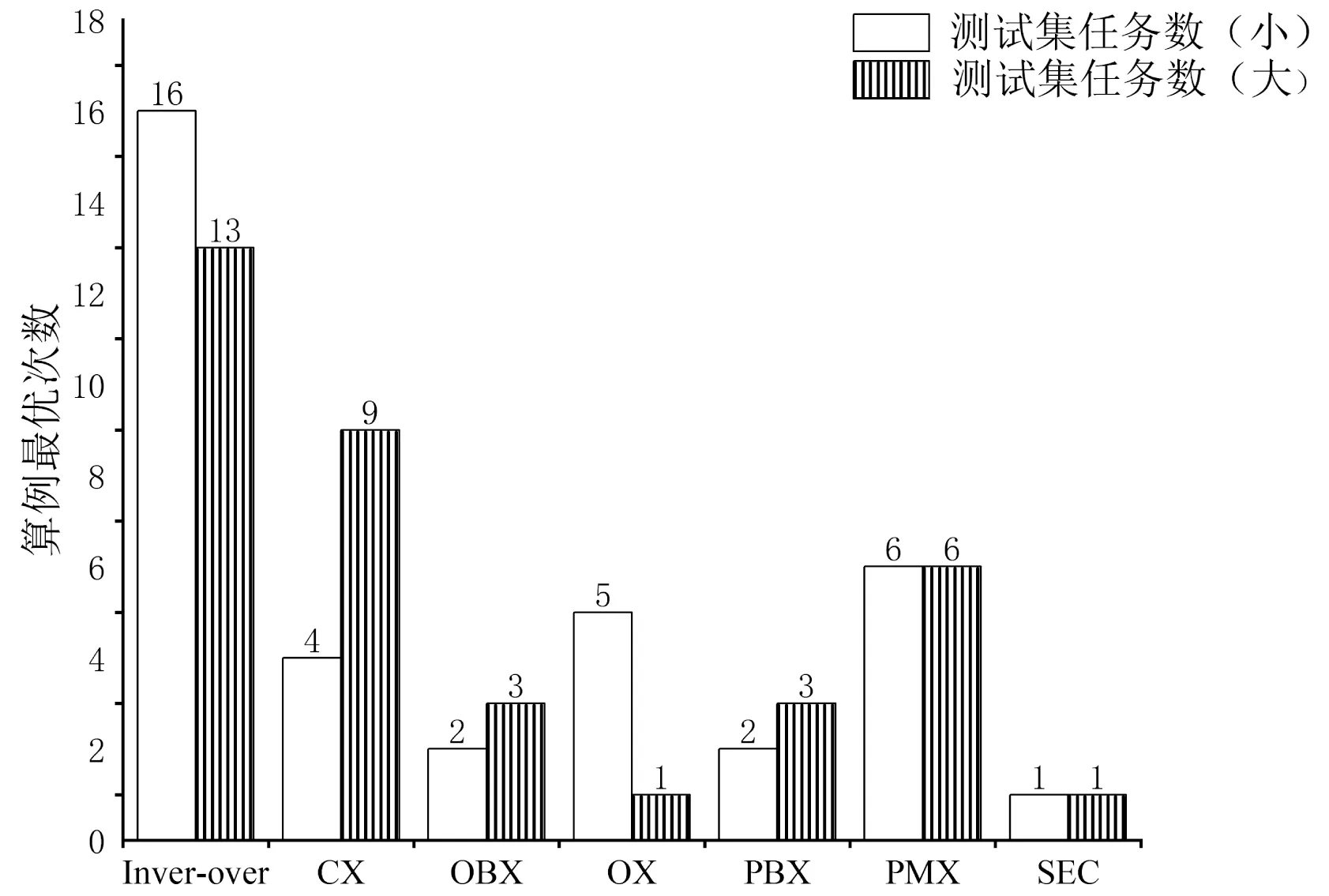
图6 测试任务集数量变化

（3）由图7～8可知，无论在实验台和被测空调数量规模处于什么情况，Inver-over算子均能取得相对于其它算法更少的耗电费用，随着实验台数量和被测空调规模的增加，Inver-over算子求解效果有所降低但是相比其他遗传算法仍然具有一定优势，而PMX、CX等能够实现区域重组交叉的算子相比于OBX和SEC等选择多基因位的交叉算子能够进行更广范围的搜索，能够更好地对实验台和测空调进行合理的分配。

图7 实验台数量变化

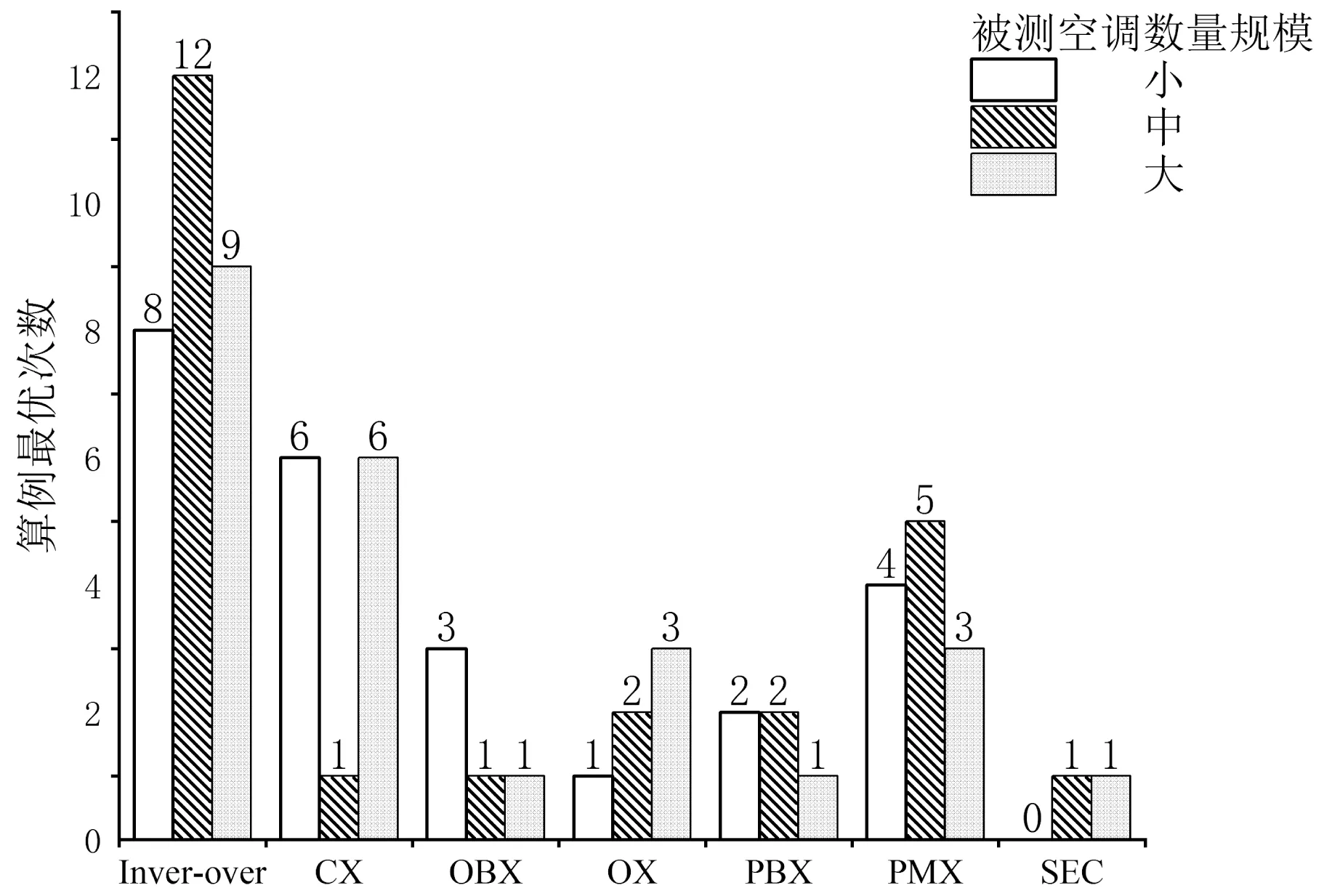
图8 被测空调数量变化

（4）由图9可知，随着空调内外机温度湿度变化增大，Inver-over算子在算例求解最优的次数上与其他算法拉开很大距离；这是由于随着温度、湿度范围变化增大，测试顺序发生变化后相邻两项各个测试项之间环境变化程度也会发生较大的改变，而Inver-over算子采用的倒置操作可以保证相邻测试项之间的环境参数不发生改变，使得种群大概率向最优解的方向进化。

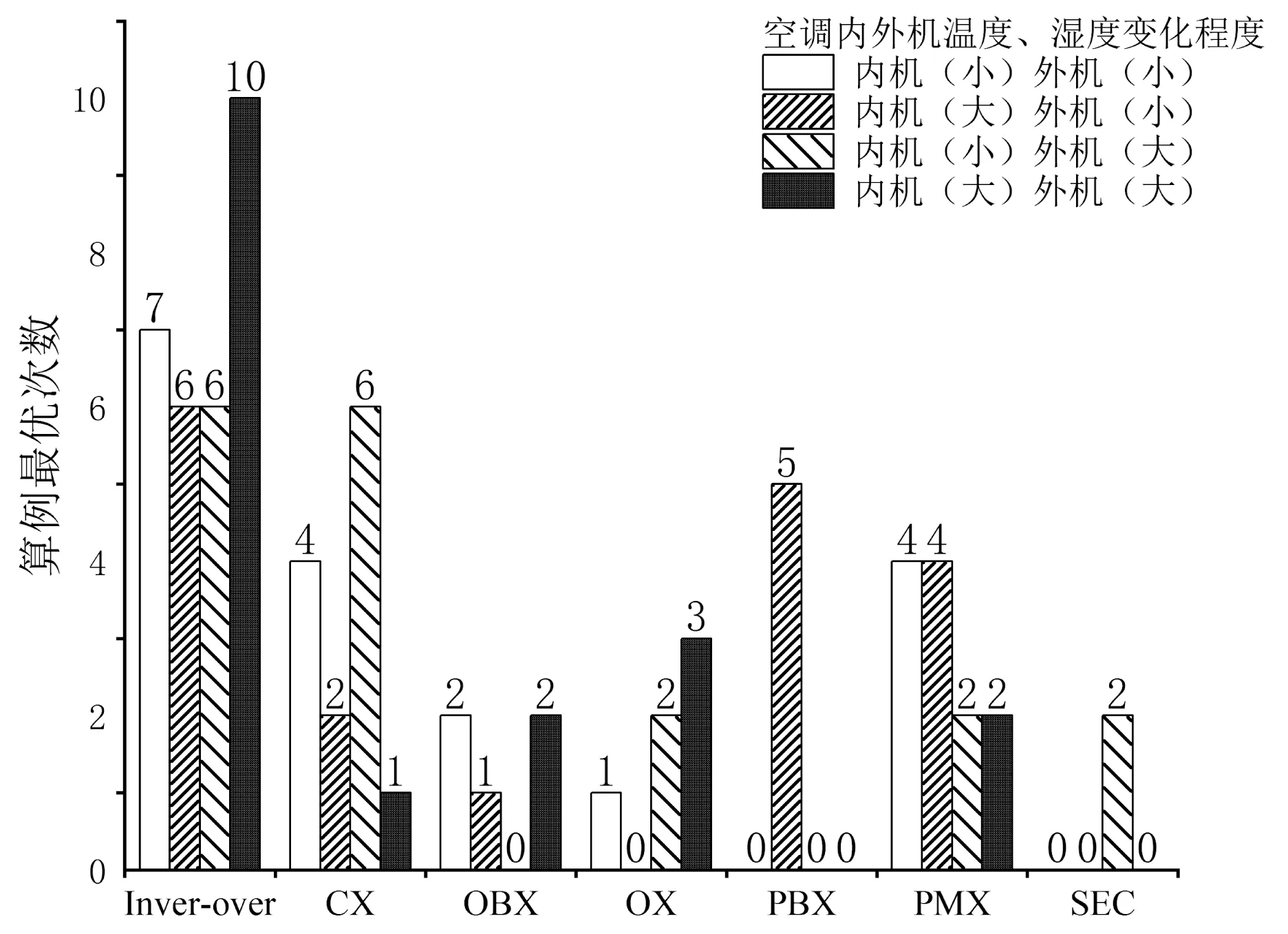
图9 空调环境参数变化

在该企业实际测试案例中，新空调测试大多需要实现测试环境在温度、湿度方面较大范围的变化，而Inver-over算子在这方面表现突出，且在其他方面相对于其他算子也具有一定的优势，于是综合上述内容选择该算子用于本文的模型求解。

3.4 算法应用及方案对比

图10所示为针对该实验中心测试任务实行安排的3种应用方案，本文随机选取10个实际案例分别计算其相对应实验台电费图。其中方案1是该企业日常空调测试安排方案，由于员工上班时长限制，该企业对任务安排的时间段没有考虑分时段电价特点，而且测试任务的顺序都是按照测试人员的经验判断，测试顺序无法达到最优，每个测试任务的“打工况”时间普遍较长，导致整个实验台耗费较高；电费成本曲线在中间位置的为方案2，一般是该企业任务加急时的方案安排，即实验台不间断进行任务测试，但测试顺序仍然是由测试人员经验判断，测试任务“打工况”时长依然没有得到优化；如图10所示，方案3电费成本曲线最优，该方案是本文针对以上2种方案进行改进后提出的RF-GA混合算法求解思路，其不仅充分利用分时段电价的特点，还由于应用该求解思路后任务“打工况”时长明显缩短，使得实验台电费得到了进一步优化。

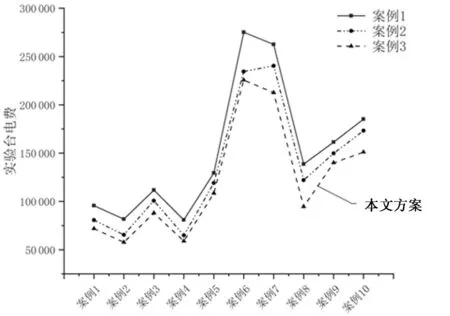
图10 3种任务安排方案相应电费

4 结束语

本文针对空调测试实验中心在空调测试任务安排时多凭工人经验、测试任务打工况时长及耗电率未知等情形，造成该企业能源消耗过多和电费支出过高的现象，以最小化实验台总电费为目标，提出了一种数据预测与智能算法深度融合的RF-GA混合算法求解思路。该求解思路不仅可以为每一台被测空调安排合理的测试顺序，使其能够充分利用分时段电价的特点；而且在空调测试顺序得到优化后，相应的测试任务参数也可以得到进一步优化（比如任务打工况时间缩短），从而使得实验台总电费在两个方面都得到了大幅度的降低。除此之外，为了满足该企业的实际测试需要，本文的预测模型和智能算法分别采用随机森林算法与Inver-over算子的遗传算法，通过该企业实际测试数据和各种具有该企业实际数据特征的测试算例中与其他算法进行比较，说明两种算法的有效性与优越性；最后通过对该企业日常任务安排方案与应用本文所提出RF-GA混合算法求解思路的方案对比，说明了本文求解方案的优越性。未来的研究包括将进一步深化GA算子与集成学习方法的结合，并进一步考虑符合人员排班后对总成本的最优化求解。