双楔形刀具侵入岩体过程仿真
2021-11-23钟自成张幼振刘焱杰王瑞泽朱国栋
钟自成, 张幼振,*, 刘焱杰, 王瑞泽, 朱国栋
(1.中煤科工集团西安研究院有限公司, 西安 710077; 2.煤炭科学研究总院, 北京 100013)
目前,在岩土工程领域获取岩土参数的方法有很多,但是在很大程度上依赖室内试验的方法,而在岩土试样制备或者运输过程中,不可避免地受到扰动影响,进而导致试样的物理参数发生变化,使得获取到的岩土参数无法准确地表征岩土的原状态指标[1]。为此,中外学者将原位测试应用于岩土工程领域,研究出静力触探、十字板剪切和旁压试验等方法,不再需要钻孔取样,避免了钻孔取样过程对原位岩土的扰动,可直接测量获取原位岩土的工程参数。
在地质勘探、油气井钻井、矿山开采、隧道掘进等领域普遍涉及机械破碎碎岩的过程,而碎岩过程多是由载荷作用下的各种刀具对岩体的压入破碎,常用的刀具形状主要有半球形、弹头形、圆柱形和楔形等[2]。鉴于楔形刀具在侵入岩体时有着良好的力学响应特性,且在滚刀刀刃破碎岩体的设计应用广泛,为楔形刀具在原位测试的应用提供了基础。
针对楔形刀具侵入岩体,中外学者开展了大量研究。文献[2]对岩石在平底圆柱形压头静压入时的2D空间应力状态和破碎过程进行数值模拟,阐述了岩石的破碎过程;文献[3]采用平行粘结细观本构模型,在岩石颗粒尺度上模拟了压头侵入岩石的破坏过程,揭示了岩石破碎漏斗的细观形成机制;文献[4]基于压头作用下岩石的破碎具有分形特性,以此来表征岩石的破碎过程。
现运用弹塑性损伤力学的本构关系来描述岩石局部脆性渐进式破坏过程,通过ABAQUS有限元仿真软件分析计算,模拟出双楔形刀具侵入岩体的过程,获得楔形刀具间距与侵入岩体特性的关系,为双楔形刀具在原位测试的应用奠定基础。
1 双楔形刀具原位测试结构设计
1.1 剪切仪结构及组成
剪切仪主要由剪切装置、加压装置、位移装置、转接头等部分组成,如图1所示。通过外接加压泵为加压装置施加压力,在位移装置的作用下,实现剪切装置上的楔形刀具作用在孔壁岩体上;变径转接头可将剪切仪与钻机连接,通过操作钻机可实现剪切仪下放到预钻孔内,也可对剪切仪进行起拔,进而实现对孔壁岩体的直接剪切破坏,进而测得岩体的工程力学参数。

图1 剪切仪示意图Fig.1 Schematic diagram of shear apparatus
1.2 侵入岩体刀具结构设计
由岩石破碎学理论中尖楔状切削具[5]在受到侵入外加载荷P侵入时岩石破碎形态可知,尖楔状切削具碎岩机理如图2所示。

α为刃角图2 楔形刀具碎岩机理Fig.2 Rock crushing mechanism with wedge cutter
剪切仪采用V形楔形刀具环向布局,其尺寸参数如表1所示。
楔状压头的长度、宽度以及刃角都对侵入岩石有着很大影响。美国科罗拉多矿业学院采用V形楔刃刀的滚刀刀盘进行的大量线性切割试验[6],V型楔刀刃角为60°~120°,刃角的不同决定滚刀与岩石的接触宽度,同时影响岩石体内的应力分布和破碎岩屑的尺度,是滚刀破岩微观机制的重要影响因素。


表1 楔形刀具尺寸参数
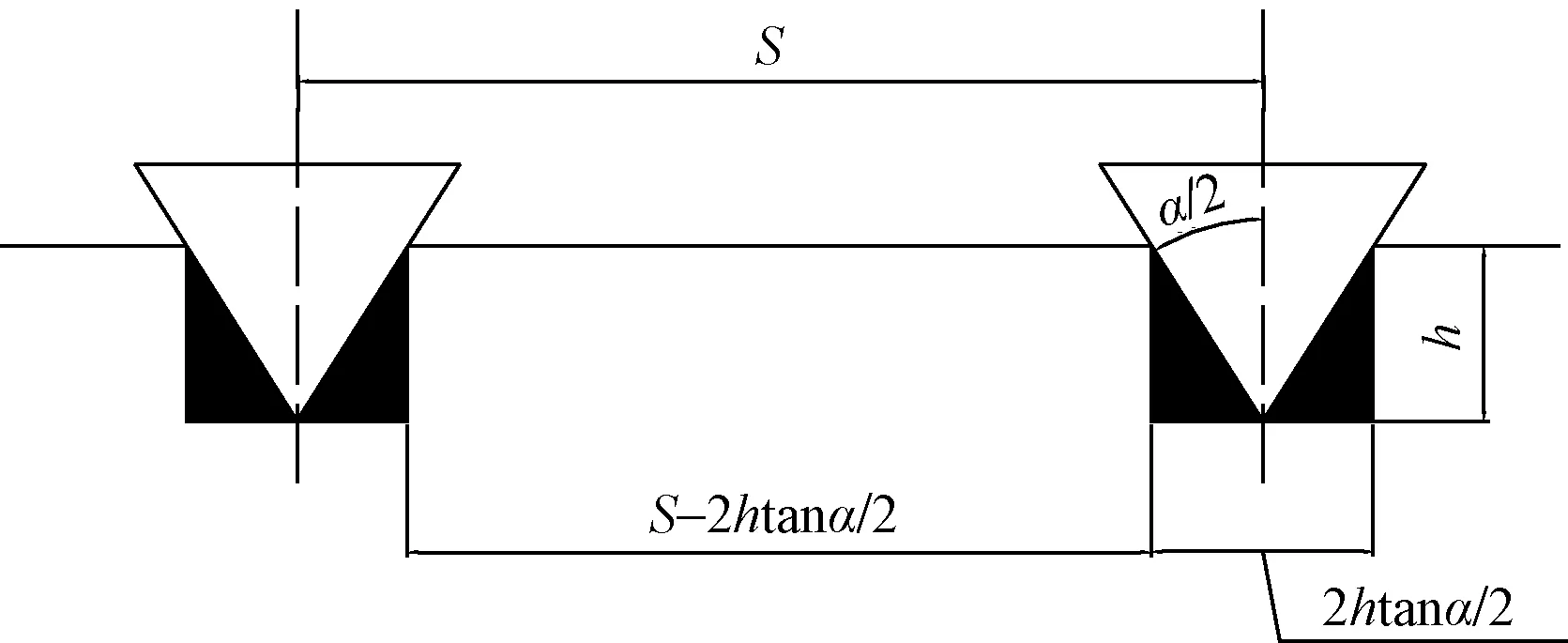
图3 楔形刀具侵入岩体示意图Fig.3 Schematic diagram of wedge cutter intruding into rock mass
2 双楔形刀具侵入岩体仿真
2.1 基本假设
以剪切仪采用的楔形刀具为研究对象,以楔形刀具侵入岩体及剪切岩体的动态载荷变化规律为目标,并获取侵入岩体的载荷位移关系。为了提高计算效率,缩短分析时间,对模型进行如下假设[7]:①岩体为连续介质,且岩体被破碎后随即被删除;②楔形刀具设为刚体,只研究楔形刀具侵入岩体及剪切岩体时岩体的破碎规律。
在载荷外加载作用下,岩体首先发生较小的弹性变形,随着载荷的增大到岩体发生屈服时,岩体由弹性变形转为塑性变形,此时岩体发生损伤,继续施加外部载荷时,岩体由于发生等效塑性应变而破坏,产生的碎块或碎屑从岩体剥离[8],因此在外部载荷作用下,岩体发生的等效塑性应变作为岩体失效时的位移,以此来作为岩体损伤失效的判定准则。ABAQUS提供的Mohr-Coulomb(M-C)模型和Drucker-Prager(D-P)模型常被运用于描述岩石塑性阶段本构关系,选用D-P模型,该模型可通过设定单元的剪切失效准则来模拟岩屑的形成和剥离过程,能够较好地模拟岩石的破坏。另外考虑摩擦力对数值模拟结果影响并不大,因此,假定楔形刀具与岩石接触面的摩擦力为0。
2.2 模型建立
以两个楔形刀具为研究对象,同时选取预钻孔三维模型的1/2,通过NX绘制后导入ABAQUS软件。由于岩体在外力作用下,不仅具有弹性变形,而且在塑性变形的同时有一定的损伤变形,因此采用综合考虑岩体应变率和损伤效应的随动塑性硬化材料模型,以塑性应变作为岩体破碎的判据,所选取的岩体为砂岩[9],密度设置为2 540 kg/m3,弹性模量和泊松比分别设置为11.54 GPa和0.062(表2),屈服应力为45 MPa,失效应变为0.02。
两楔形刀具侵入岩体位移最大为5 mm,整个侵入岩体加载过程采用位移控制加载,步长为0.25 mm,固定岩体除外侧表面其余四周边界,选用Hex单元类型和C3D8R六面体单元[10],网格总节点数为1 978 788,单元数为1 927 400。图4为两楔形刀具轴向间距为30 mm时,与岩体网格划分后结果。

表2 岩石与楔形刀具参数

图4 楔形刀具与岩体网格划分二维示意图Fig.4 Two-dimensional schematic diagram of wedge cutters and rock mass meshing
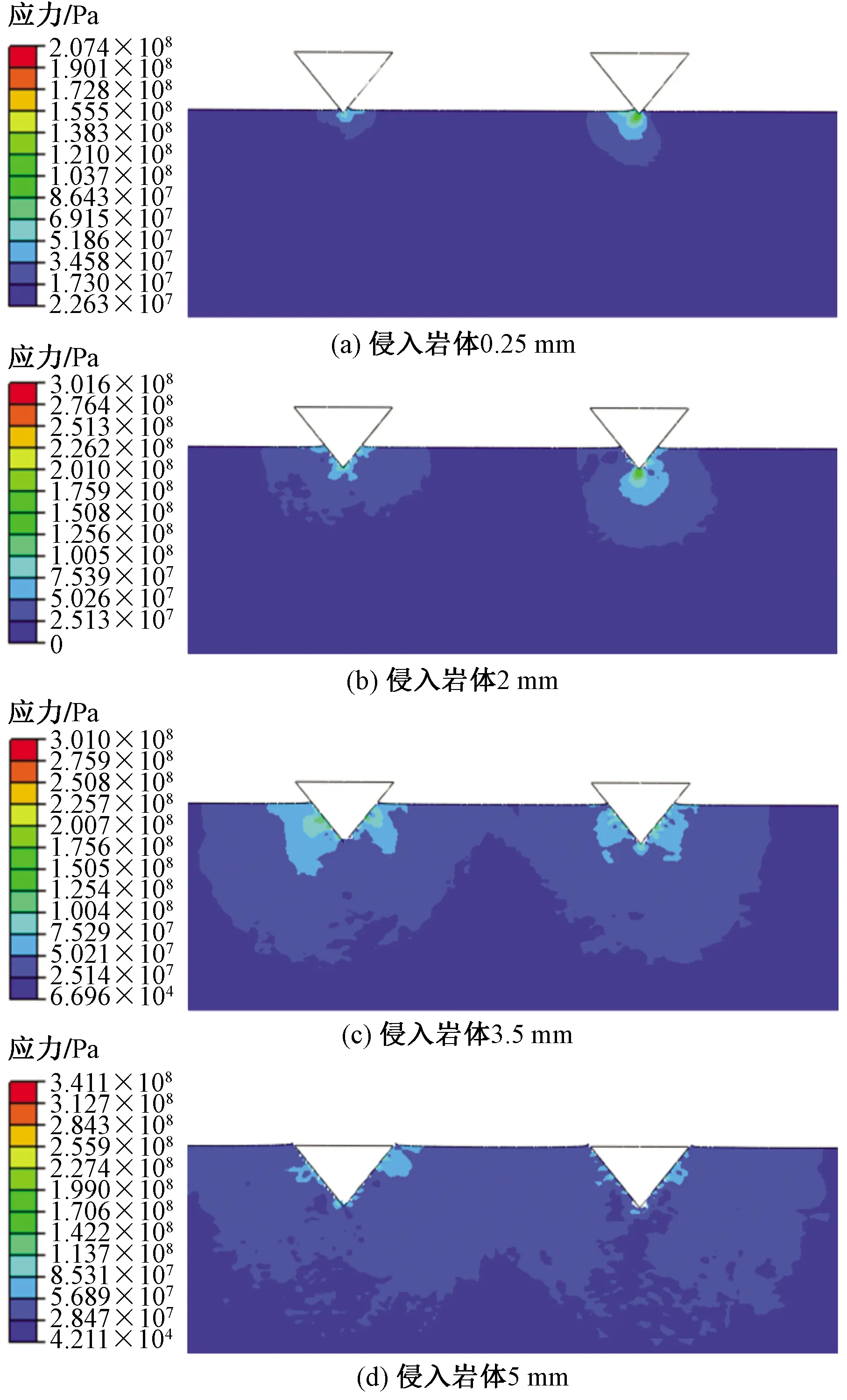
图5 楔形刀具轴向间距30 mm侵入岩体截面应力云图Fig.5 Stress cloud diagram of intrusive rock mass section with 30 mm axial spacing of wedge cutters
3 仿真结果分析
3.1 侵入岩体过程仿真
由于楔形刀具设定为刚体,因此仿真时楔形刀具无变形,且无应力和应变,所以选取岩体的破碎过程作为研究对象进行分析。图5(a)、图5(b)、图5(c)和图5(d)分别为楔形刀具间距30 mm时的侵入岩体0.25、2、3.5、5 mm的岩体应力云图。图6(a)、图6(b)、图6(c)和图6(d)分别为楔形刀具间距30 mm时的侵入岩体0.25、2、3.5、5 mm的岩体破碎坑环向应力云图。
随着楔形刀具压入岩体时,如图5(a)所示,楔形刀具的尖端最先与岩体接触,在其前方出现袋状密实核,同时环向孔壁上有两条环向应力区域,如图6(a)所示,随着侵深的增加,密实核发生损伤变形,随着楔形刀具其上的作用力越来越大,岩体所受应变超过其等效失效塑性应变时,即可触发单元删除命令将其破碎单元删除,进而在孔内岩壁上形成两个破碎坑,如图5(b)和图6(b)所示。随着楔形刀具逐渐侵入到岩体中,楔形刀具两侧参与破碎岩体的面积增加,破碎坑的应力区也随之增加,并向两侧扩散,密实核旁侧初始孤立的网格逐渐受到侵入破碎的作用,破碎坑的面积和体积进一步增大,如图5(c)和图6(c)所示,但其中心位置的岩体单元只有在侵深继续增加并发生接触时才会发生损伤变形,进而破碎删除。由于岩体网格划分为六面体单元,破碎坑呈阶梯状,但崩碎形成的岩体破碎坑坑呈楔形状,楔形刀具与岩体重复经历着弹性变形、压皱压裂和体积破碎3个阶段[11],如此循环重复,不断产生新的破碎坑,如图5(d)和图6(d)为侵入5 mm时形成的破碎坑形态。
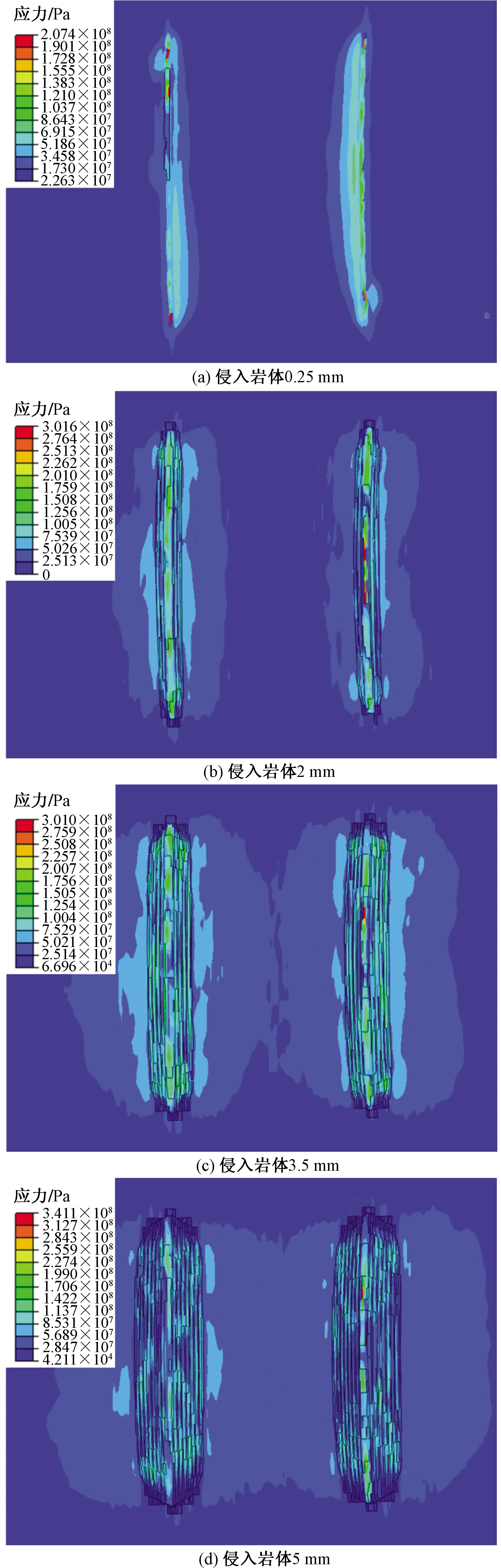
图6 破碎坑环向应力云图Fig.6 Circumferential stress cloud diagram of broken pit
3.2 侵入岩体动态载荷
图7为楔形刀具间距l分别为10、20、30、40、50 mm时,径向载荷随侵入位移变化的关系曲线。可以看出,楔形刀具侵入岩体的动态载荷呈跳跃变化的,这是由于楔形刀具侵入岩体时,先在其上形成密实核,此时楔形刀具载荷呈线性增加,当密实核四周岩体发生剪崩时,载荷急剧下降,再随着侵深的增加,进而形成新的密实核。
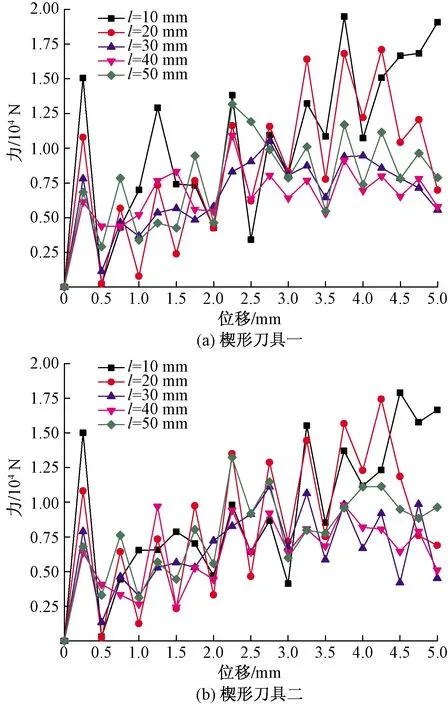
图7 双楔形刀具侵入岩体径向载荷动态响应曲线Fig.7 Dynamic response curve of radial load of double wedge cutters intruding into rock mass
4 结论
(1)基于岩石破碎学理论中尖楔状切削具侵入时岩石破碎形态,采用V形楔形刀具作为剪切仪侵入岩体的设计,能够保证侵入岩体良好的特性。
(2)以楔形刀具不同间距侵入孔壁岩体进行数值模拟仿真分析,仿真结果表明:楔形刀具侵入岩体具有跃进型,且重复经历着弹性变形、压皱压裂和体积破碎3个阶段,如此循环重复,不断产生新的破碎坑,环向破碎坑与楔形刀具结构相符。
(3)以楔形刀具不同间距侵入孔壁岩体的动态响应曲线表明:当间距在30~50 mm变化时,轴向间距越小,楔形刀具侵入岩体相互作用明显,侵入岩体所需的侵入载荷越大;但当间距在30~50 mm变化时,侵入载荷降低的趋势在减弱,在砂岩的原位剪切试验中,楔形刀具间距选用30~40 mm为宜。
