明晰试验过程 理解等可能事件
2021-11-23文/姜炜
文/姜 炜
等可能条件下的概率计算,能够直接求出概率,避免了大量重复试验。但在实际运用的过程中,“等可能”这个前提往往容易被忽视。理解“等可能”,我们才能更准确地解决问题。
一、明晰试验过程,找出等可能事件
例1 一只不透明的袋子中装有2 个白球和2 个红球,这些球除颜色外都相同,搅匀后从中任意摸出1 个球,记录颜色后放回、搅匀,再从中任意摸出1 个球,求两次都摸到红球的概率和一次摸到白球一次摸到红球的概率。
【解析】袋子内共有4个球,摸出1个球便有4 种等可能的结果,为了区别,把球编号:白1、白2、红1、红2。本题试验分两步,依次去看第一次摸球的等可能事件与在第一次的基础上第二次摸球的等可能事件,列出表格并表示出所有结果如下:
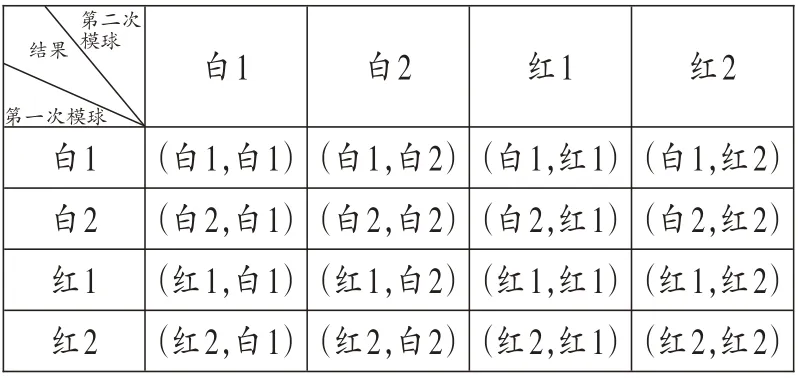
结果第二次模球白1白2红1红2第一次模球_________________________________________________________________白1_____________白2__________红1__________红2(白1,白1)(白2,白1)(红1,白1)(红2,白1)(白1,白2)(白2,白2)(红1,白2)(红2,白2)(白1,红1)(白2,红1)(红1,红1)(红2,红1)(白1,红2)(白2,红2)(红1,红2)(红2,红2)
也可画树状图如下:
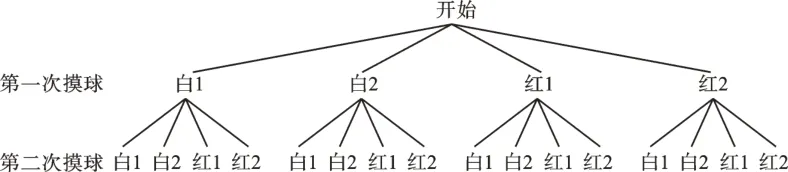
树状图的结果数与列表相同,共有16 种结果,由于每一步列出的都是等可能事件,故这16 种结果是等可能的。注意,在这样的有序思考下,顺序不同,结果也是不同的。比如第一次摸到红球,第二次摸到白球,和第一次摸到白球,第二次摸到红球,看颜色都呈现一红一白,但是摸出的个体不同、过程不同,不能混为一谈。

【点评】本题按试验步骤将表格分为两个维度,或者将树状图分成两个层次,依次写出每一步等可能的结果。这样一来,不同的个体和过程算作不同的等可能结果。
二、理解题意,认清现象与本质
例2 如图1,一个小球从M处投入,通过管道自上而下落到A或B或C处。已知小球从每个岔口落入左右两个管道的可能性是相等的,求投一个小球落到B的概率为______。
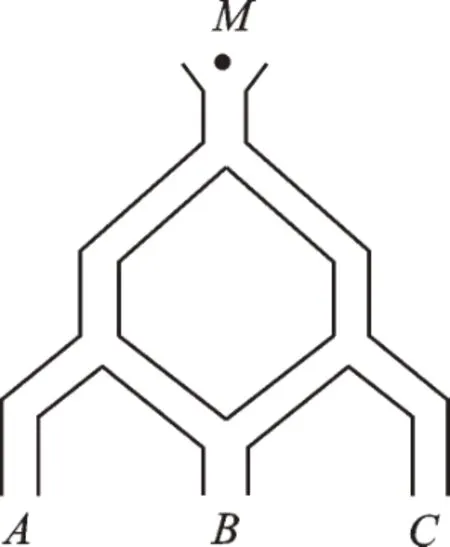
图1
【解析】从结果来看,小球落到A、B、C处有3 种可能,但它们的可能性大小并不相等。已知小球从每个岔口落入左右两个管道的可能性相等,那我们便以这个等可能事件为基础去分析。球下落时经过两次岔口,如图2,有①②③三个岔口,给管道标记字母,画出树状图。
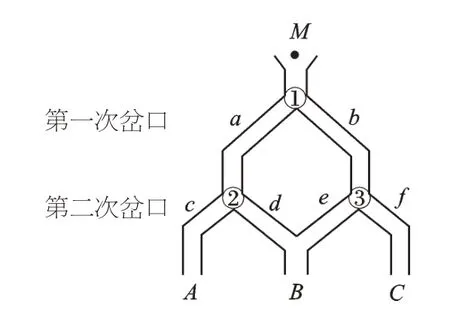
图2
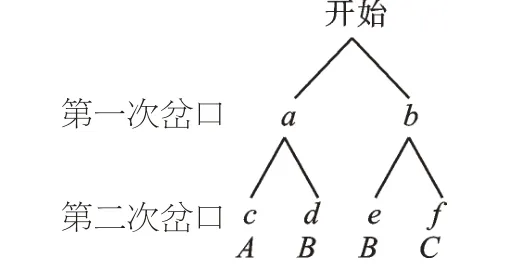


【点评】考虑等可能事件不能只看最终的表象,要根据整个试验过程,选准关键节点考虑等可能的情况。
三、拓展模型,化无限为有限

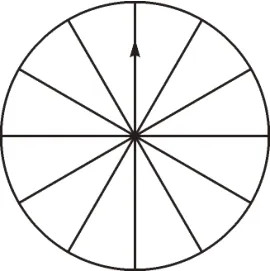
图3

