正确理解概念 轻松避免错误
2021-11-23王怡蕴
文/王怡蕴
了解数据的集中趋势和离散程度,可以帮助我们从不同的角度认识数据,掌握处理数据的方法,并做出合理的推断和预测。同学们只有明确概念、理解各数意义,才能轻松地避免错误。
例1 一次数学考试中,九年级(1)班和(2)班的学生人数分别为52、48,平均成绩分别为85 分、80 分,则这两个班的平均成绩为 。

【错因剖析】平均数是刻画数据集中趋势时一个常用的统计量,在日常生活中应用较为广泛。同学们比较熟悉的是算术平均数。而平均数的大小不仅受一组数据中各个数值大小的影响,而且与各个数值在一组数据中的“重要程度”有关,也就是与“权”有关。
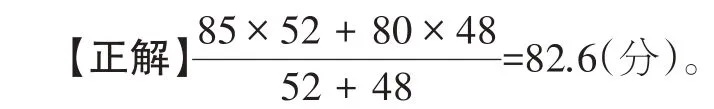
例2 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示。这些成绩的中位数是 。

【错解】97。
【错因剖析】将一组数据按大小顺序排列,如果数据的个数是奇数,那么处于中间位置的数叫作这组数据的中位数;如果数据的个数是偶数,那么处于中间位置的两个数的平均数叫作这组数据的中位数。错解中未将所有数据按大小顺序排列,只算了100、98、96、94 这四个数的中位数。
【正解】共有25个数,最中间的数为第13 个数,是96,所以这组数据的中位数为96分。
例3 若数据8,9,7,8,x,3 的平均数是7,则这组数据的众数是________。
【错解】8。
【错因剖析】一组数据中出现次数最多的数据叫作这组数据的众数。特别注意,众数可能不止一个。错解未根据概念先算出x,只根据表面数据就判断众数。
【正解】由平均数为7,得8+9+7+8+x+3=7×6,
解得x=7。
∵这组数据中7和8出现次数最多,
∴这组数据的众数为7和8。
例4 若一组数据x1,x2,x3,…,xn的方差为5,则另一组数据2x1+3,2x2+3,2x3+3,2x4+3,…,2xn+3的方差为________。
【错解】2×5+3=13。
【错因剖析】当数据都加上一个数(或减去一个数)时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘一个数(或除以一个不为0 的数)时,平均数也乘或除以这个数,方差变为这个数的平方倍。
【正解】∵x1,x2,…,xn的方差是5,
∴数据2x1,2x2,2x3,…,2xn的方差是4×5=20,
∴数据2x1+3,2x2+3,2x3+3,2x4+3,…,2xn+3的方差是20。
