序列Kriging仿真优化方法综述

师路欢，李耀辉，吴义忠，王书亭

（1.许昌学院电气（机电）工程学院，河南 许昌 461000）

（2.华中科技大学国家企业信息化CAD应用支撑软件工程技术研究中心，湖北 武汉 430074）

1 引言

随着设计层次的提升，最优性能备受。因知识缺乏及设计误差，产品性能将出现偏移甚至导致失效。尽管计算能力持续增强，诸如Ansys等软件对复杂产品的仿真仍非常耗时。因此，利用Kriging 近似复杂仿真的优化方法成为产品设计领域的热点[1-2]。主要利用试验设计、Kriging及潜在估计信息实现仿真的近似、空间探索及优化，具有缩短设计周期、降低研发成本、提升设计精度等特点，适合解决昂贵估值的计算机仿真问题，并广泛应用于航空航天、机械工程等诸多领域。鉴于此，对序列Kriging的仿真优化方法进行综述。

2 试验设计及Kriging模型

2.1 试验设计

试验设计（DoE：Design of Experiments）[3]通常以较少试验次数、较短周期和较低成本来获得理想结果。全因子设计将试验各因素在不同水平下进行组合产生采样点，建模精度较高，但非常耗时，仅用于因素数与水平数较少场合。又出现基于效应稀疏原理和投影特性的部分因子设计、中心复合试验设计和Box-Behnken试验设计。但所获取的设计点缺乏独立性、随机性和均匀性。为此，基于全空间填充、非重叠采样的拉丁超立方设计（LHD）[4]得到广泛应用。与此相近的正交试验设计可根据正交性从全因子试验设计中挑出均匀分散、齐整可比的采样点，是一种高效率经济的DoE方法。

2.2 Kriging模型

对于m个设计点X=[x1，...，xm]T，X∈ℜm×n和目标响应Y=[y1，...，ym]T，Y∈ℜm×1，经典Kriging[5]的数学表达为：

式中：μ(x)—趋势函数；z(x)—数据观测及相关性量化后建立的随机过程，其均值及方差分别为0和σ2。

当μ(x)等于0、μ和时，分别称为简单Kriging、普通Kriging和标准Kriging模型。任意采样点x与w之间的相关性用协方差E[Z(x)Z(w)]=σ2R(θ，ω，x)表示，通过优化相关参数θ，能够自适应调整设计点之间的相关性。空间相关函数控制着Kriging 的平滑度、样本间的相互关系及量化观测值间的相关性。

对任意x∈ℜn，(x)被看作能够找到最佳线性无偏估计λT(x)Y的一个随机函数，这相当于最小化均方误差MSE[(x)]=E[λT(x)Y-y(x)]。受无偏估计的约束限制，还需满足E[λT(x)Yy(x)]=0。且任意点的Kriging表达如式（2）所示。

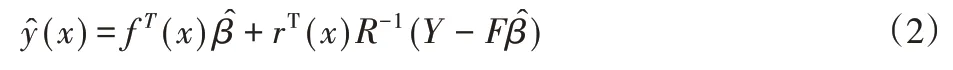
式中：r(x)={R(x，x1)，···，R(x，xn)}T；向量矩阵F由回归函数f(x)组成；半正定对称矩阵R由所有已知点之间的自相关性和互相关性组成的最小二乘估计和高斯随机过程方差的估计可由式（3）和（4）计算获得。

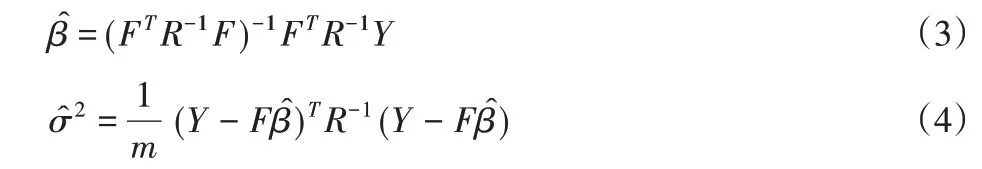
经典Kriging对趋势函数选择、模型精度提高及随机噪声等问题存在不足。为此对Blind、随机、Co-Kriging进行综述。

2.2.1 Blind Kriging 模型

Kriging模型难以预测计算机仿真的全部行为并选择合适的回归函数。Blind Kriging 就是利用贝叶斯特征选择方法拓展了经典Kriging。Blind Kriging［6］通过捕获样本数据中最大方差来确定基函数。为此，需考虑一系列候选回归函数。理想情况下，样本数据完全通过所选回归函数来表示，而Kriging中的随机部分对上述过程仅有较小影响或几乎没有影响。

构造Blind Kriging经三个阶段：（1）构造初始Kriging，并对相关参数进行最大似然估计；（2）依据估计系数，利用更好的回归特征函数扩展初始Kriging的回归函数，同时产生一系列Kriging；（3）最后，根据交叉验证所估计的误差决定有效的Kriging是否停止构造或改善。当误差满足要求，选择当前最佳回归特征函数集构造最终Blind Kriging。

2.2.2 Co-Kriging模型

为探索精确与粗糙模型数据的相关性来，以提高模型的预测精度。Co-Kriging[7]通过已知样本集和Xe=，分别根据经典Kriging 模型建立低保真度模型yc=和高保真度模型。

建模思路如下：首先利用粗糙数据(Xc，yc)创建经典Kriging模型Yc(x)，然后通过精确数据和粗糙数据间的残差(Xe，yd)构造第二个Kriging模型，其中yd=ye-ρμc(Xe)，桥接参数ρ是第二个Kriging模型中最大似然估计的一部分。两个Kriging模型回归函数和相关函数的选择等设置依据粗糙数据和残差分别进行各自调整。

2.2.3 随机Kriging模型

当出现随机仿真或存在噪声情况下，前述Kriging将无法得到正确结果。因此，随机Kriging 更接近标准的高斯回归过程。通过独立的高斯过程ζ(x)建立均值为0、协方差矩阵为Λ的噪声模型，即ζ～N(0，Λ)建立随机Kriging。与通用Kriging模型相比，表达式所增加的类似于信噪比矩阵。

2.2.4 三种新Kriging模型的优缺点

为说明三种新Kriging的优缺点，首先，利用Brain作为测试函数，基于相同的初始LHD、最大方差采样和最终采样点数，对标准Kriging、Blind Kriging和随机Kriging模型进行测试比较。其函数图、梯度图和方差梯度图，如图1所示。

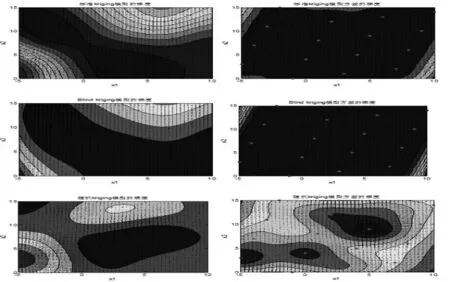
图1 标准Kriging、Blind Kriging和随机Kriging的近似结果Fig.1 Approximate Results of Standard，Blind，and Random Kriging

从图1可看出，Blind Kriging的近似精度最高，但搜索合适的回归函数需要耗费较长时间。标准Kriging 的精度稍差，但与Blind Kriging相比，精度差别并不明显，因此，Blind Kriging适合更高精度要求的场合。而加入噪声的随机Kriging的近似效果与噪声均值和方差有必然联系，适用具有一定分布规律的噪声函数。然而，随机Kriging可能存在重复仿真，这使设计者在面对实际复杂的黑箱仿真时无法接受，而重复仿真的解决有待于设计者进一步探索和研究。对Co-Kriging，高低保真度函数的使用无法用二维函数表示。因此，选用一维函数，其近似结果，如图2所示。

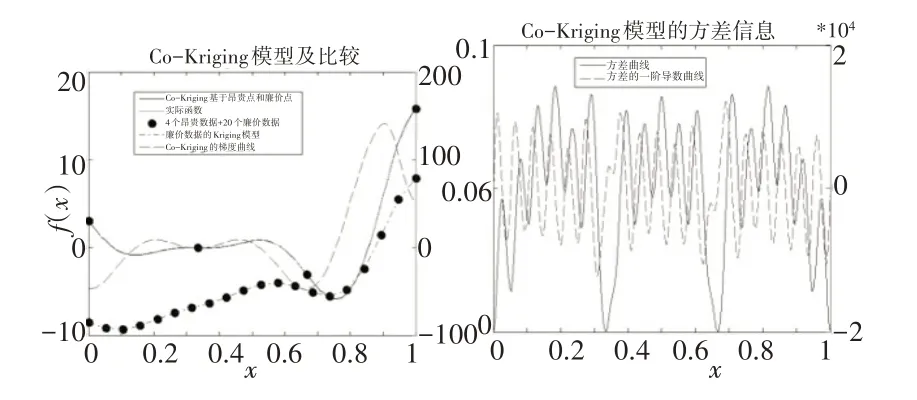
图2 Co-Kriging模型的测试结果Fig.2 Test Results of the Co-Kriging Model

Co-Kriging的拟合精度更好，但需要具有“廉价”估值并建立两个Kriging，也需要更大的计算成本。但在高精度仿真模型的近似中，Co-Kriging在近似效果、收敛精度以及实际应用性方面通常好于Blind Kriging。

3 序列Kriging的仿真优化方法

3.1 算法基本框架

依据更新次数，序列Kriging的仿真优化分为一次DoE和序列Kriging优化。较早的一次DoE优化方法以全局近似后的Kriging作为优化目标，利用全局优化方法直接获取近似最优解。实际上，为保证Kriging更接近实际仿真模型，需要对DoE过程进行优化，使最终DoE数据能够更均匀、正交的分布到整个设计空间。但可能存在仿真估值次数过多、所构造Kriging无法正常使用、部分采样点信息量过小以及优化收敛速度过慢或过早收敛等缺点。

多数研究者使用序列Kriging优化方法[9]。仿真估值次数严格受限于时间成本，导致优化方法仅在Kriging最优点附近进行更新和细化。因此，该方法利用已知数据信息和Kriging自身参数特征来有效地指导迭代优化搜索朝向具有更大潜在信息量的采样点，以减少仿真估值次数并快速收敛到全局最优解。设计者如何通过加点采样准则减少昂贵估值次数以及如何跳出局部最优区域一直是序列Kriging优化的研究热点。序列Kriging仿真优化的基本框架，如图3所示。

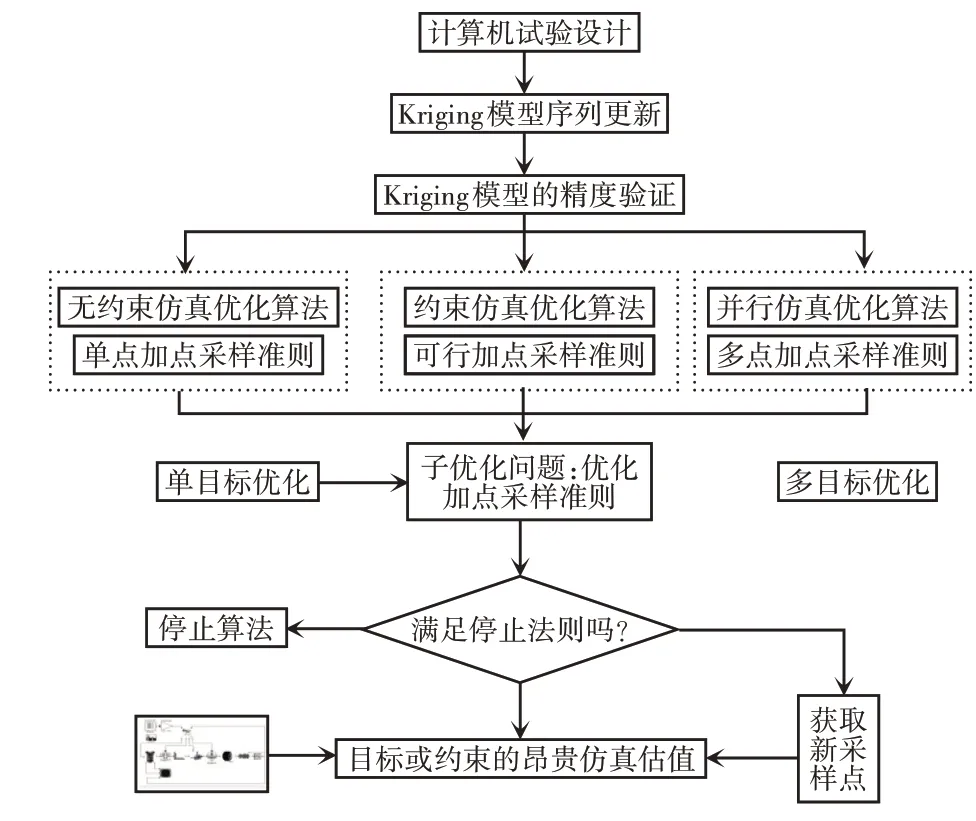
图3 序列Kriging仿真优化方法的基本框架Fig.3 The Basic Framework of Sequence Kriging Simulation Optimization

Step 1：初始DoE及Kriging建模。利用DoE中的设计方法获取初始样本点，在对这些样本点仿真之后，建立初始的Kriging。

Step 2：模型验证。在未知设计点处，利用方差等信息对Kriging模型进行精度验证，并作为算法是否停止的一种判别准则。

Step 3：子优化问题。根据不同优化问题，通过Kriging相关信息建立加点采样准则，并利用单/多目标全局优化算法对该准则进行优化采样，获取新的迭代点。

Step 4：停止准则。根据子优化问题条件，判断收敛精度或最大仿真次数是否满足要求，满足时停止算法，否则，继续。

Step 5：更新Kriging 模型。对新获取的采样点进行仿真估值，并加入到数据样本集中，利用新的数据点重新构造Kriging模型，并为下一次的子优化做好准备。

结合图3，对序列Kriging的无约束优化、约束优化及多点并行仿真优化的进展及最新算法分别进行阐述。

3.2 序列Kriging仿真优化方法

3.2.1 序列Kriging的无约束优化方法

最早序列Kriging 优化是在每次迭代过程中产生一个采样点。目标均值采样准则通过最小化Kriging 目标来获取更优化点。然而，真实模型与Kriging之间的最优值存在差异，过多强调目标估计而忽视不确定性因素可能导致局部最优。因此，出现通过最大化Kriging 估计方差来进行序列优化采样[10]。然而，完全强调全局搜索与优化Kriging目标一样糟糕。上述两种思路在提高优化效率和收敛精度方面能力有限。为此，文献[11]提出了工程应用较为广泛的无约束EGO方法。结合Kriging预测目标的最小化及采样位置的不确定性构造出期望改善EI（Expected Improvement）作为加点采样准则，找到一个具有较大不确定性且较小函数值的设计点。然而，EI或Kriging模型的多峰性与复杂性将增加优化成本，初始样本的欺骗性会产生较小的标准差估计，这可能导致仅最优解附近的数据点才具有较大EI值，在进行更全局的搜索之前，初始最优解的附近区域将不得不进行更为细致的搜索。

最近，REGIS开发了一种命名为TRIKE（的无约束全局优化方法[12]，并应用于在陡峭又狭窄的全局最小盆域及高维度优化问题中。为每次迭代中，该方法在可信区间内使用信任域策略去最大化EI函数来获取下一个迭代点，并根据EI实际改善的比率进行信任域区间大小的调整。在一些情况下，使用新的初始填充设计重新开始序列Kriging 的优化算法要胜于继续寻找全局最优点。在计算昂贵的数据集中，使用新填充设计的重启策略似乎不符常理。但是，文献[13]所作的数值测试强有力证明：当算法处于停滞状态，重启策略能够更好地让算法继续进行下去，特别是陡峭而狭窄的全局最小盆域。这种方法看似有悖常理，但其成功部分源于以下事实：序列Kriging的优化方法对初始空间填充设计的使用相当敏感。对给定的测试问题，在一种空间填充设计中利用序列Kriging的优化方法可以快速找到全局最小解，利用同样方法在另一个空间填充设计中将可能花费相当长的时间。当算法在迭代过程中不再有所改善时，通过重启策略，全局最小值的平均函数估值次数将大幅减小。

尽管EGO的全局收敛性已经确立[14]，但测试结果显示：EGO在某些常用测试问题中具有较慢的收敛性。但在概率意义上，重启策略的成功应用可解释为：在一定假设下，算法找到全局极小或接近最优解的运行次数符合几何概率分布。对给定确定的初始空间填充设计，TRIKE算法也是确定的。然而，如果使用一个随机变化的初始空间，那么TRIKE 的行为就像一个随机算法。因此，重启策略使优化方法再次收敛到全局最小值成为可能。此外，文献[15]结合Kriging和遗传算法提出一种具有稳健搜索能力和良好近似性能的优化算法；文献[16]利用混合模型（Kriging 和RBF）提出了一种自适应序列全局优化方法。还有结合对偶原理、Kriging模型和信任域策略形成的基于Kriging和对偶变化的全局优化方法[17]。

3.2.2 序列Kriging的并行仿真优化方法

像EGO 和TRIKE 这样的优化算法在一次迭代过程中只能增加一个新采样点，对于复杂的仿真优化问题，这需要花费几周或者更长时间来完成全局寻优。为提高优化效率和收敛速度，可通过在一次循环中获取多个采样点并进行并行仿真的序列Kriging并行仿真优化方法实现。

由Jones提出的EGO并行方法通过使用超出不同给定目标的改善概率来选择不同采样点[18]，但其性能的优劣与设定目标的阀值水平相关。后来，Chaudhuri等人[19]提出一种自适应的目标设置方法在每次EGO的迭代循环中灵活运用PI加点准则来获取多个采样点。文献[20]使用多目标的加点采样准则来有效提高改进EGO方法的自身寻优能力。文献[21]将Kriging的有效全局算法运行到多个代理中，其中一个循环周期内的采样点数目由代理模型的数量决定。

Ginsbourger教授结合混合蒙特卡罗采样和分析边界策略提出的一种并行期望的异步优化方法[22]；基于不确定性逐步减小策略，还提出了几个新的多点加点采样准则[23]，特别适合计算成本昂贵的并行仿真优化。最具有代表性的并行仿真优化思想是其所提出的相信趋势函数的KB（Kriging Believer）策略和利用参数进行持续欺骗的CL（Constant Liar）策略[24]，它们都可通过最大化q-EI加点准则获取q个采样点。

KB利用Kriging对采样点的预测均值替代每次迭代后所选择采样点的响应值，以更新Kriging，进而获取更多新采样点。多点问题(x′n+1，..，x′n+q)=argmaxX′∈DqEI(X′)的第一种近似求解方法：（1）建立KB(X，Y，q)函数；（2）i=1，i从1到q，做q次循环：①，方差取该点的预测方差；③X=X ⋃{xn+i}，Y=Y ⋃{μ(xn+i)}；④循环结束。（3）函数结束。在d维优化上依赖已知EI的贯序策略利用可接受的计算成本提供q个设计点存在失败风险，因为信任普通Kriging的估计值可能使观测数据过冲，从而导致陷入非最优区域。为此，又出现降低这种风险的CL策略。

利用给定值L（称为“谎言”）在每次迭代时更新元模型的CL策略在每次迭代具有相同值L，即：最大化EI找到xn+1好像一直满足y(xn+1)=L，L∈R。实现步骤如下：（1）建立函数CL(X,Y,q)；（2）i=1，i从1 到q，共做q次循环：①xn+i=argmaxx∈DEI(x)；②X=X⋃{xn+i}，Y=Y⋃{L}；③循环结束。（3）函数结束。该策略的关键是不同L对最终优化性能的影响。从min{Y}，mean{Y}和max{Y}选一，也可根据权重大小自适应获取L。

针对Kriging并行仿真优化的其他思路，文献[25]利用多个初始点优化方法搜索Kriging模型的局部最优解，并围绕局部最优解的附近区域作进一步搜索，以实现多点采样；文献[26]通过最小化目标和最大化EI获得两个设计点完成并行采样；文献[27]提出了多点加点序列优化采样方法；文献[28]人对序列Kriging 的并行全局优化进行了综述。

尽管上述方法在迭代优化过程中能获取多个采样点，但捕获采样点所具备的有效信息量不高，也没有对这些采样点作进一步的筛选，因此，序列Kriging的并行仿真优化方法仍具有潜在的研究价值。

3.2.3 序列Kriging的约束优化方法

在约束条件已知情况下的序列Kriging优化容易实现。当约束是黑箱时，需要对约束函数进行Kriging 的近似来完成寻优。因此，兼顾约束边界、点的可行性等因素的约束优化方法值得研究者深入研究。

针对序列Kriging的约束优化，文献[29]通过EGO方法引入七种加点采样准则，并对这些准则如何影响全局或局部搜索行为进行详细的阐述；文献[30]利用Kriging 所提供目标和约束函数的全局估计以及广义的EI加点采样准则提出一种约束优化方法，达到减少目标及约束函数昂贵估值次数的目的。文献[31]通过新加点采样准则在可行域内找到Pareto最优解进行昂贵黑箱约束问题的处理；梯度优化方面，文献[32]依据EGO和基于梯度的优化方法，通过对初始点变异方法、多元插值与非插值响应面函数的研究以及Kriging模型参数的估计，提出了一种基于广义灰箱约束模型的全局优化方法。针对限制全局优化求解的可行性因素，文献[33]通过自适应抽样搜索并确定多个可行性区间，然后在每个可行区间进行局部寻优。文献[34]阐述了目前常用的几种优化加点准则及其相应子优化问题的求解与约束处理。

上述约束优化方法只对约束问题的处理提供了一种思路或者只能处理某些简单的仿真优化问题。且对初始样本中是否存在可行采样点以及对其进行判断和搜索等问题都没有作具体的考虑和设计。在目标和约束都为黑箱情况下，无法找到合适的加点采样准则来平衡全局与局部搜索行为。鉴于此，文献[35]初步实现一种序列Kriging的约束全局优化方法，能够在初始DoE不存在可行点的情况下完成寻优。此外，Kriging与其他元模型进行混合的全局优化算法也有所发展，比如自适应混合元模型全局优化算法[36]采用外点罚函数方法来处理约束优化问题。

（1）单点采样的约束优化[37]

通常，黑箱函数f(x)的约束全局优化由式（5）表达。

其中，约束向量g(·)中每个约束将由Kriging近似。加点采样准则的子优化问题必须考虑约束。整合约束信息主要有两种策略：第一种是评估约束可行性的概率[38]，第二种是在加点采样准则的子优化中直接使用约束Kriging的均值。

a）可行性概率方法

假定Kriging 对第i个约束的预测均值和方差用(x)和(x)表示，则该约束的可行性概率可由式（6）表示。

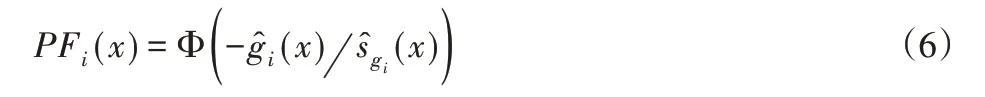
通过EI乘以任意点的可行概率，可将EGO中EI的约束优化问题转化为一个无约束优化问题。为此，对m个约束的优化问题，其加点采样准则的表达如式（7）所示。

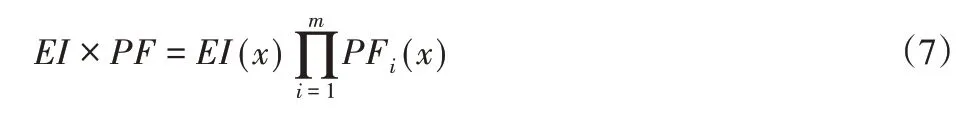
在任何约束条件的可行性非常低的情况下，将迫使EI的大小变为零。因此，可行性概率对EI值的影响比较强烈，并且使得算法无法探索接近约束边界的点。

b）约束EI法（即直接使用约束Kriging均值的方法）

这种处理约束的方法如式（8）所示。仅仅将EI优化作为一个约束优化问题来解决。由于Kriging均值直接作为约束条件，因此高度依赖于约束Kriging模型的精度。如果约束处于起作用状态，则会添加接近(x)=0的采样点。

注意，当出现不连续可行区域且没有找到可行点，文献[39]建议使用可行性概率来获得一个可行初始点。

c）期望违背（EV-Expected violation）

文献[40]利用期望违背EV代替Kriging约束均值提出一种自适应约束优化方法。其中EV的定义如式（9）所示。

EV 类似于EI准则，约束也要使用Kriging 模型。在没有约束违背的区域有较高的EV值，即该区域具有较高的不确定性。如果EV高于给定阈值，则可认为该采样点是可行的。那么，新的EI优化问题定义为：

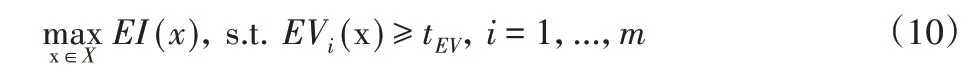
上述三种优化方法效果相当，约束EI法效果略好。

（2）多点采样之双目标约束优化

上述的单点采样方法难以在求解可行性和约束条件之间取得平衡。双目标约束优化不再将约束问题转化为无约束优化问题，是将EI和PF作为独立目标进行优化。如式（11）。

通过考虑获得目标函数的最小值和满足约束条件获取一组Pareto集。所构建Pareto集可让用户从多目标优化后的大量采样点中筛选出更合适的采样点。而在EGO算法中，只能选择满足两个目标之间可以接受的一个采样点。需要着重强调的是，使用式（5）的单目标方法确定的单个采样点与Pareto前沿找到的点并不对应。单目标优化函数是严重多峰的，因此将问题视为多目标可以得到更好的采样点。式（11）的表达可限制PF所允许区域，因优化过程可忽略不起作用约束。然而，在优化之前并不清楚是否为起作用约束，这也限制其适用性。可行性概率的标准形式表明：Kriging 所的估计约束限制区域将小于实际约束限制区域。如果所有不起作用约束都被忽略，那么剩下的约束可以看作等式约束，并且远离约束边界的模型精度并不需要给予太多关注。

（3）基于EI、PF和约束预测方差的三目标约束优化方法

在单目标和双目标优化方法中，没有考虑约束Kriging模型的预测方差。如果某些区域的方差较大且存在全局最小值，则可能会阻止优化过程在足够的置信度下找到最优值。在起作用约束下，减少预测方差可能会产生更接近实际约束边界的最小值。因此，除双优化目标之外，还可使用第三个目标，即最小化约束Kriging模型的预测方差。约束Kriging的预测方差可以直接用作第三个优化目标，如式（12）所示。另一种方法是使用EV 准则（式9）中的第二部分，如式（13）所示。

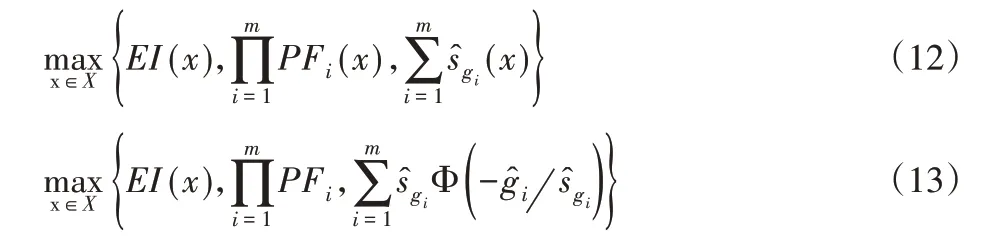
由于仅增加Kriging的预测方差作为第三个优化目标，从Pareto集选择的点仍然隶属于双目标Pareto集中的一部分。

3.2.4 三类优化方法的优缺点

对于无约束的TRIKE算法，利用对称LHD选择2（n+1）个初始设计点，并通过基准测试函数Branin、Goldstein Price、Hartman3、Hartman6 与EGO 在相对误差小于1%条件下进行平均估值次数及标准的比较，以展示TRIKE特点，如表1示。

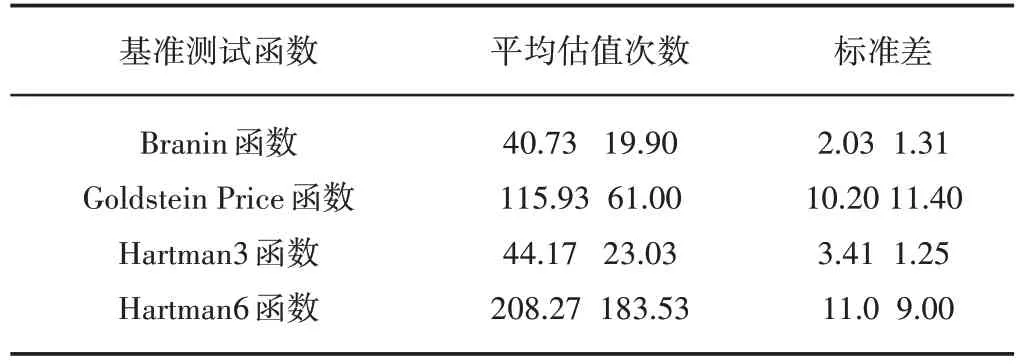
表1 TRIKE（左）和EGO（右）的比较结果Tab.1 Comparison Results of TRIKE and EGO

与EGO相比，TRIKE在局部优化策略上产生了本质性的改善。特别对于高维问题，TRIKE更优于EGO。因此，调整搜索区间的自适应信任域策略更适用序列Kriging的无约束优化，且对陡峭而狭窄的全局最小盆域和高维的Kriging优化问题具有更好的适用前景。然而，对具有几个局部最优解且平坦的Goldstein Price函数具有略差的优化效果。

以Branin-Hoo 为基准测试函数，以3×3全因子DoE 作为初始采样，让四种策略（包括CL 的三种变化策略L=min（Y）、L=max（Y）和L=mean（Y）及KB 策略）在每次循环中增加四个采样点，比对PI和EI进行比较结果，如图4所示。

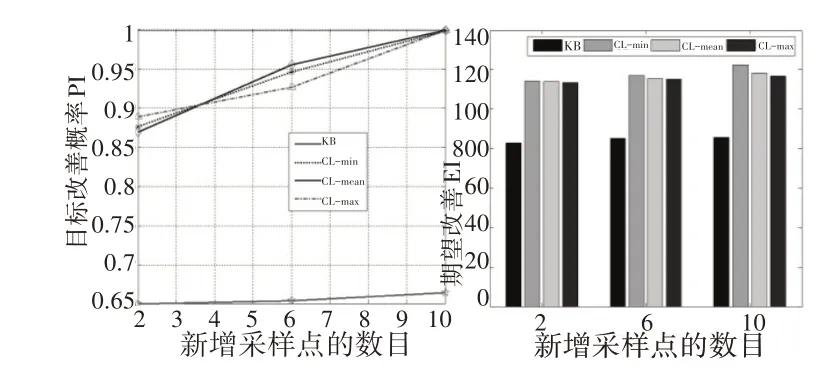
图4 KB和CL在采样过程中PI（左图）与EI（右图）的比较结果Fig.4 Comparison of PI（left）and EI（right）in KB and CL during Sampling

结果显示，四种策略都为优化问题提供了空间填充、探索性设计和概率改善。CL[min（Y）]在所考虑的策略中给出了最好的实际改善。新增10个采样点后，它访问了测试函数的三个局部最优区域。随着采样点的增加，PI和EI也逐渐增大，且CL策略对已经访问的采样点会产生排斥。此外，还可以看出，在q-EI标准中，当q增加时，EI的值变化比较小。这较好说明q-EI准则是一种拒绝不恰当采样点的策略。

存在缺点是：当q增加时，三个CL策略的PI迅速收敛并接近1，从而无法区分采样点的好坏。根据1改善程度，q-EI更适合进行采样点的选择。此外，由于几乎所有采样点都被困于初始最优点附近，KB策略的测试结果不尽如人意。

对于约束优化问题，LHD 选择10个初始采样点，设置最大函数估值次数为35，然后对单采样点及基于多目标的多采样点优化方法进行测试，主要对搜索到的最优解离真实函数最优点的距离、近似约束函数的精度以及最优值附近的均方根误差进行对比，以说明其优缺点结果，如表2所示。

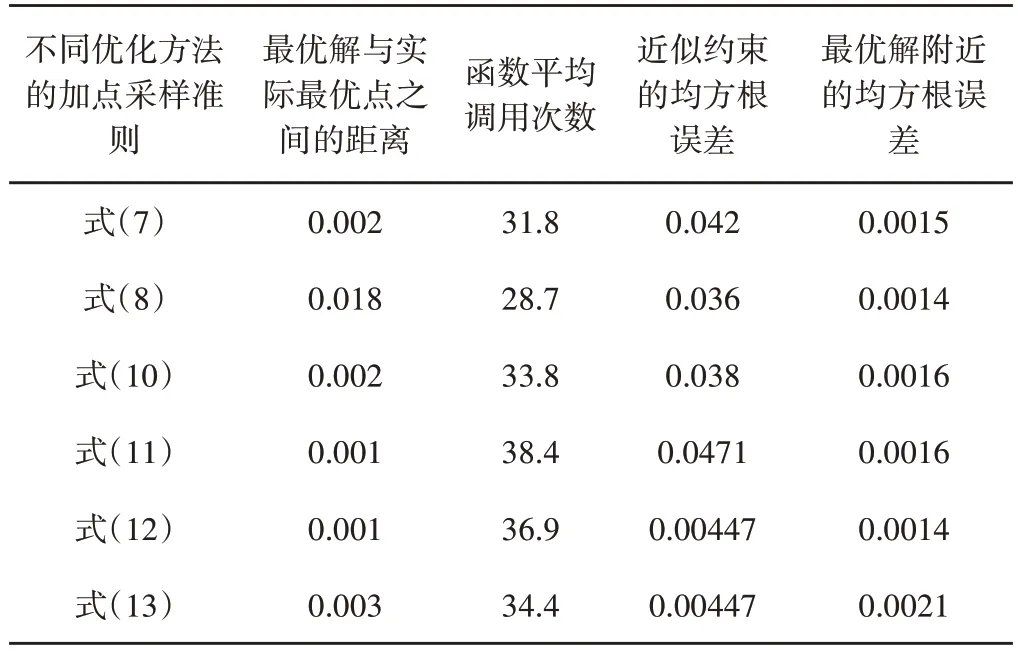
表2 针对优化问题（5）七种优化方法的比较结果Tab.2 Comparison Results of Seven Methods for Problem（5）

这些约束优化方法中，双目标EI和PF法给出较好结果。三目标准则提供与双目标方法等价的最优估计，但约束预测的准确性更好。第二个三目标准则在整个空间得到最好的约束精度，但其对约束搜索给予太多关注，导致略差的最优值估计。此外，最优解附近的均方根误差表明，单目标优化方法主要聚集在最优解附近进行更优点的搜索，在均衡全局与局部搜索行为方面，多目标优化显示了更大的优越性。总之，单目标优化具有较少的函数调用次数，而多目标具有较好的优化结果。对于将约束Kriging的预测方差直接用作第三个优化目标的约束优化方法，这三个优化目标的关系，如图5所示。

从图5可看出：在约束Kriging的预测均方差的影响下，三个目标的Pareto 前沿数据相当于从原双目标Pareto 前沿中删除了一些采样点。输入方面，在约束Kriging预测准确性较高的情况下，来自Pareto前沿的点将更加分散，这有助于减少约束边界的不确定性。总之，多个目标优化选择多个采样点的优化法方法明显优于单个目标获取一个采样点的优化方法。

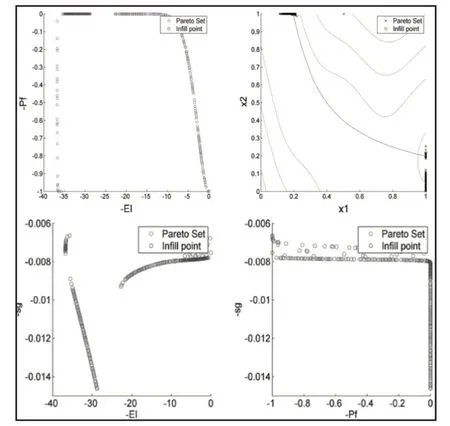
图5 利用Kriging预测均方差作为第三个目标的优化方法的测试结果Fig.5 Result on Optimization Using Predicted MSE as Third Objective

3.3 算法终止条件

序列Kriging仿真优化的终止条件考虑以下三方面：（1）Kriging的精度是否满足给定精度要求；（2）是否达到最大昂贵仿真次数；（3）一些参数值（比如均方根误差等）是否小于给定容差。通常使用交叉验证法（CV-Cross Validation）[41]和均方根误差（RMSE）估计法[42]对Kriging模型进行评价。

由于序列Kriging仿真优化的目的是在较少昂贵估值下获取全局近似最优解，因此，最大昂贵仿真次数是常用的优化停止条件，昂贵仿真次数的多少通常与优化问题或实际实验的维度和复杂度相关。如果超出，利用Kriging近似模型进行仿真优化将毫无意义。此外，设计者更热衷于使用优化过程中的某些参数是否小于给定容差作为停止条件，比如期望改善EI小于0.001、两次获得的最优解相差甚小等等。然而，对于实际测试问题，设计者通常会将上述终止准则中的两个或多个结合起来使用，当任何一个条件满足时，就停止优化。

4 软件工具箱

Kriging在近似计算密集的仿真模型中备受欢迎。为了给设计者提供方便，序列Kriging仿真优化方法的工具箱包括：

（1）DACE 工具箱。DACE 是Matlab 工具箱，用于计算机仿真模型的Kriging近似。该软件包括DoE方法。软件下载请访问http：//www2.imm.dtu.dk/projects/dace/。

（2）DiceKriging 及DiceOptim 工具。DiceKriging 和DiceOptim是两个R语言软件包，用于近似和优化昂贵估值的确定性目标函数。DiceKriging 工具箱对各种Kriging 模型进行模拟、预测和验证。DiceOptim 能够基于EI的单点和多点采样准则完成序列Kriging 的全局优化。软件包下载请访问https：//cran.r-project.org/web/packages/DiceKriging/index.html和https：//cran.r-project.org/web/packages/DiceOptim/index.html。

（3）ooDACE工具箱。基于Matlab的ooDACE工具箱提供了强大、灵活且易于扩展的框架。不同类型的Kriging在同一平台下通过面向对象的方式实现。可以完成Co-Kriging、随机Kriging、Blind Kriging、梯度增强Kriging 和通用Kriging 的近似建模，高效的超参数仿真优化。还可以利用交叉验证、积分的均方差等精度预测方法对模型进行评估。软件包下载请访问http：//sumo.intec.ugent.be/ooDACE_download。

（4）SuperEGO工具箱。SuperEGO也是基于Matlab语言，将智能采样策略、Kriging建模方法、诸如Direct算法的全局优化方法以及优化终止条件整合在一起完成通用Kriging的全局近似及仿真优化。该软件包并不公开，如果仅用于个人或教育用途，可向开发者获取。

（5）Surrogates optimal toolbox 等。基于Matlab 的Surrogates optimal工具箱主要适用于连续、整数或混合整数变量且计算昂贵的黑箱全局优化问题。对于计算成本低的函数评估，工具箱的优化效果可能不是非常有效。软件包下载可访问https：//sites.google.com/site/srgtstoolbox/。

5 总结与展望

序列Kriging的仿真优化方法一般只需要少量昂贵估值就能够明显看出函数趋势且快速得出结论。基于序列搜索的优化过程中，近似的Kriging模型能够在未采样点处为优化提供预测目标和方差的估值，这些信息结合有效的全局优化方法能够在平衡全局与局部搜索行为的基础上搜索合适的全局近似最优解，有效促进了对模型的直觉理解和开发。

针对序列Kriging仿真优化方法，还面临许多挑战：

（1）关于Kriging 模型中相关矩阵R 的病态问题。理论上，Kriging 的相关函数是完全单调的，因此，R 应保证是半正定的。而相关矩阵出现异常可能存在两种原因。第一，如果函数非常平滑且可预测，那么样本点将会高度相关，这意味着相关矩阵的每一列几乎是一个全为1的列，从而导致这些列的极高共线性；第二，优化运行接近尾声时，算法所增加的点往往接近先前的采样点。当两个采样点非常接近的时候，R中与这些采样点相应的列将几乎是一样的，导致R出现奇异情况。如果仅仅是计算Kriging目标估计及其标准差的话，这种病态是易于管理的，但计算边界时，将产生较大麻烦。

（2）EGO中期望改善函数的复杂性。EGO方法在一些情况下确实能够找到较好近似最优解。但因EI函数的复杂性和多峰性可能导致较长的优化时间。此外，初始样本的欺骗性可能会产生较小的标准差估计，这往往导致算法更多地关注局部探索区域，直到这种不确定性变得很小。结果，仅仅接近当前最优解的数据点有大的EI值。而且，在初始Kriging已经获得精确最优解的情况下，EGO没有任何优点。因此，如何选择有效的加点采样准则来保证EGO在恰当的时候合理跳出局部最优区域一直是设计者研究的重点和难点。

（3）并行优化采样具有更大的发展潜力。相对于昂贵仿真估值，优化时间的消耗几乎可以忽略不计，每次迭代获得q个设计点的采样准则将使总优化时间减少为原来的近1/q。目前大多数优化方法在每次迭代中仅产生一个新采样点，或者所获取的多个采样点无法定位到设计空间的不同盆型区域，从而导致搜索到的多个采样点无法为循环优化提供更多有价值的信息。如何利用深度技术在序列迭代中产生多个更优前景的采样点，以提高优化效率和收敛精度，有待于进一步研究。

（4）约束为黑箱优化问题处理。目标和约束的黑箱性将导致序列Kriging约束优化方法的优化难度骤然增加，大多文献只对约束问题的处理提供了一种思路或者只能处理某些特殊问题。且对初始样本中是否存在可行采样点以及对其进行判断和搜索等问题很少作具体的考虑和设计。特别在目标和约束都为昂贵黑箱条件下，无法找到合适的加点采样准则来平衡全局与局部搜索行为。这为该方向的深入研究留下充足空间。