偏压作用下碳纤维布加固H型钢柱承载力分析

刘斐然， 雷宏刚*， 完海鹰

(1.太原理工大学土木工程学院， 太原 030024； 2. 合肥工业大学土木与水利工程学院， 合肥 230009)

目前中国存在大量钢结构建筑，许多建筑需变更其使用功能或是遭受腐蚀、地震、自然灾害等因素影响，需要进行加固处理。

传统的加固方法主要通过螺栓连接或焊接的方法将钢板安装到需要加固的位置进行补强。这种方法在施工上和耐久性上均存在许多问题。钢板的起吊和安装较为复杂，同时安装钢板还会额外增加结构的自重。增加的钢板也易受腐蚀，这导致后期维护费用较高，因此这不是一个理想的方案[1]。

近20年来，纤维增强聚合物(fiber reinforced polymer，FRP)复合材料在土木工程领域已用于建造新结构和修复现有老化基础设施之中。FRP复合材料具有较好的耐久性，对裂纹扩展、腐蚀、冲击和疲劳载荷有足够的抵抗能力，增加了结构的能量吸收能力[2]。

在众多FRP加固材料之中，碳布纤维(carbon fiber reinforced polymer，CFRP)逐渐成为最经济同时也是应用最为广泛的材料。CFRP材料的密度仅为钢材的20%，但其抗拉强度远高于钢材抗拉强度。此外CFRP抗腐蚀能力强，抗疲劳性能优越。因此许多专家学者对CFRP加固混凝土和钢结构构件展开了大量的研究。张泽福等[3]进行了CFRP 加固钢筋混凝土小偏心受压柱承载力试验研究并给出了CFRP 加固不同混凝土强度等级和偏心率的钢筋混凝土构件的加固效果。孙国帅等[4]进行了碳纤维增强聚合物-钢管混凝土柱轴压稳定性分析，证明了CFRP可以有效地改善结构的性能等结论。王庆利等[5-6]研究得出了纵向CFRP可以显著提高试件刚度结论并总结了典型的圆CFRP-钢管混凝土受弯构件的弯矩-曲率关系曲线的特点。Teng等[7]研究了用纤维增强聚合物复合材料加固钢结构的问题。Huang等[8]研究了CFRP网格混凝土剪力墙在横向循环荷载作用下的性能。Al-Mekhlafi等[9]进行了偏心荷载下CFRP加固不锈钢短柱的试验研究。Peiris等[10]研究了用超高模量碳纤维层压板加固钢梁的效果。Li等[11]进行了腐蚀对CFRP与钢黏结性能影响的实验与数值研究。目前关于CFRP加固钢结构的研究还不成熟，故现对CFRP加固的受压H型钢柱的稳定承载力进行探究。展开CFRP加固偏压H型钢柱承载力公式的推导工作，同时设计偏心距为10 mm和20 mm共6组试验进行探究CFRP对H型钢柱承载力的提升幅度。通过理论推导与试验研究探究CFRP材料对H型钢柱的加固效果以及提出可以预测加固效果的理论计算公式。以期为实际加固工程提供理论基础。

1 试验研究

1.1 试验准备

试验共采用6根H型钢柱。6根钢柱的几何参数相同：钢柱长L=1 500 mm，H型钢截面高h=100 mm,宽b=100 mm，翼缘厚tf=8 mm,腹板厚tw=6 mm。H型钢柱采用Q235B钢材，CFRP布采用日本东丽UT70-30(300 g/m2)[12]其厚度为0.167 mm，钢材和CFRP布的力学性能指标分别如表1和表2所示。试件参数如表3所示。

表1 H型钢柱钢材力学参数Table 1 Mechanical parameters of H-shaped steel column

表2 碳纤维布力学参数Table 2 Mechanical parameters of carbon fiber cloth

表3 试件参数表Table 3 Specimen parameter list

从许多专家学者对CFRP的研究中可以看出CFRP布可以在一定程度上提高构件的承载力，但是随着构件外表面碳纤维布层数的不断增多，每层加固对应的承载力提升幅度不断减小[4-9]。因此现研究粘贴1～3层CFRP布对偏压H型钢柱承载能力提升的幅度(偏心加载在强轴方向)。文献[13]通过单搭接剪切试验，研究了胶黏剂(高强度韧性胶黏剂和低模量脆性胶黏剂)的韧性和胶黏剂厚度对CFRP与钢材黏结性能的影响，选取了厚度为 0.2 mm的结构胶进行粘接。

采用的H型钢柱因有强弱轴之分，所以在柱子两端焊接两块端板。将两块端板沿着强轴方向开槽，加载采用的端板如图1所示，加载采用的刀铰支座如图2所示进行加载。这样既可以达到试件两端铰接的目的，又可以保证柱子在受力过程中沿着强轴屈曲。

图1 加载端板图Fig.1 Load end plate diagram

图2 刀铰支座图Fig.2 Hinge support diagram

钢柱中部应变片位置如图3所示，采用CFRP布纵向粘贴法(沿着柱高方向，只粘贴翼缘)，在粘贴过程中保证粘贴的质量，铲除气泡并及时养护。当CFRP布粘贴和养护完成之后，将CFRP布表面也粘贴一定数量的应变片，钢柱中部CFRP布表面应变片布置如图4所示。

M-4～M-10 为相应位置应变片编号图3 H型钢柱中部应变片布置图Fig.3 Layout of strain gauges in the middle of H-shaped steel column

MC-3、MC-4均为相应位置应变片编号图4 H型钢柱中部CFRP布表面应变片布置图Fig.4 Layout of CFRP cloth surface strain gauges in the middle of H-shaped steel column

1.2 试验过程

试验开始前先将碳纤维布面积等代成钢材面积，估算试件的极限承载力F,在75%F之前，每级加载5 kN,持载30 s后记录数值。当荷载超过75%F后每级加载2.5 kN持载60 s后记录数值。试验加载装置如图5所示，试验现象(图6)如下所述，CFRP布发生剥离或是出现褶皱后试件失稳破坏，试件两端端板均向偏心方向倾斜，但无明显破坏现象。

图5 加载器械及构件Fig.5 Loading equipment and components

图6 试件破坏现象Fig.6 Destruction of the specimen

Z-1C10D试件在加载前期无明显现象，荷载达到390 kN时CFRP布开始发生局部破坏，荷载达到400 kN时CFRP布持续发生局部破坏。当荷载达到425 kN时CFRP布出现褶皱现象，荷载增加到440 kN时CFRP布与H型钢柱剥离。

Z-2C10D试件当荷载达到365 kN时CFRP布开始发生局部破坏，荷载达到460 kN时柱顶和柱底靠近端板处的CFRP布开始出现剥离现象，荷载达到465 kN时柱中CFRP布开始剥离。

Z-3C10D试件在荷载达385 kN时CFRP布开始发生局部破坏,荷载达482 kN时柱中和柱顶靠近端板处的CFRP布发生剥离现象。

Z-1C20D试件在荷载达280 kN时CFRP布开始发生局部破坏，当荷载增加到383 kN时柱底部位的弯曲外侧CFRP布鼓起，荷载达397 kN时柱中处CFRP布发生剥离。

Z-2C20D试件在荷载达300 kN时CFRP布开始发生局部破坏，荷载增加到407 kN时柱中部位CFRP布出现褶皱。

Z-3C20D试件在荷载达315 kN时CFRP布开始发生局部破坏，荷载增加到432 kN时试件产生平面内弯曲，柱中CFRP布开始剥离，柱顶部位的CFRP布产生轻微鼓起。

1.3 试验结果

1.3.1 钢柱纵向应变

图7为Z-1C20D试件中部受压应变情况，其他试件的应变曲线大致相同。其中M-5为弯曲外侧，M-9为弯曲内侧。从图7可以看出，开始加载时H型钢柱两侧均受压。当荷载接近极限承载力时，钢柱侧向位移不断增加，弯曲内侧持续受压，弯曲外侧由受压状态变成受拉状态，随后钢柱达极限承载力，柱子中部位移迅速增加，试件整体失稳破坏。

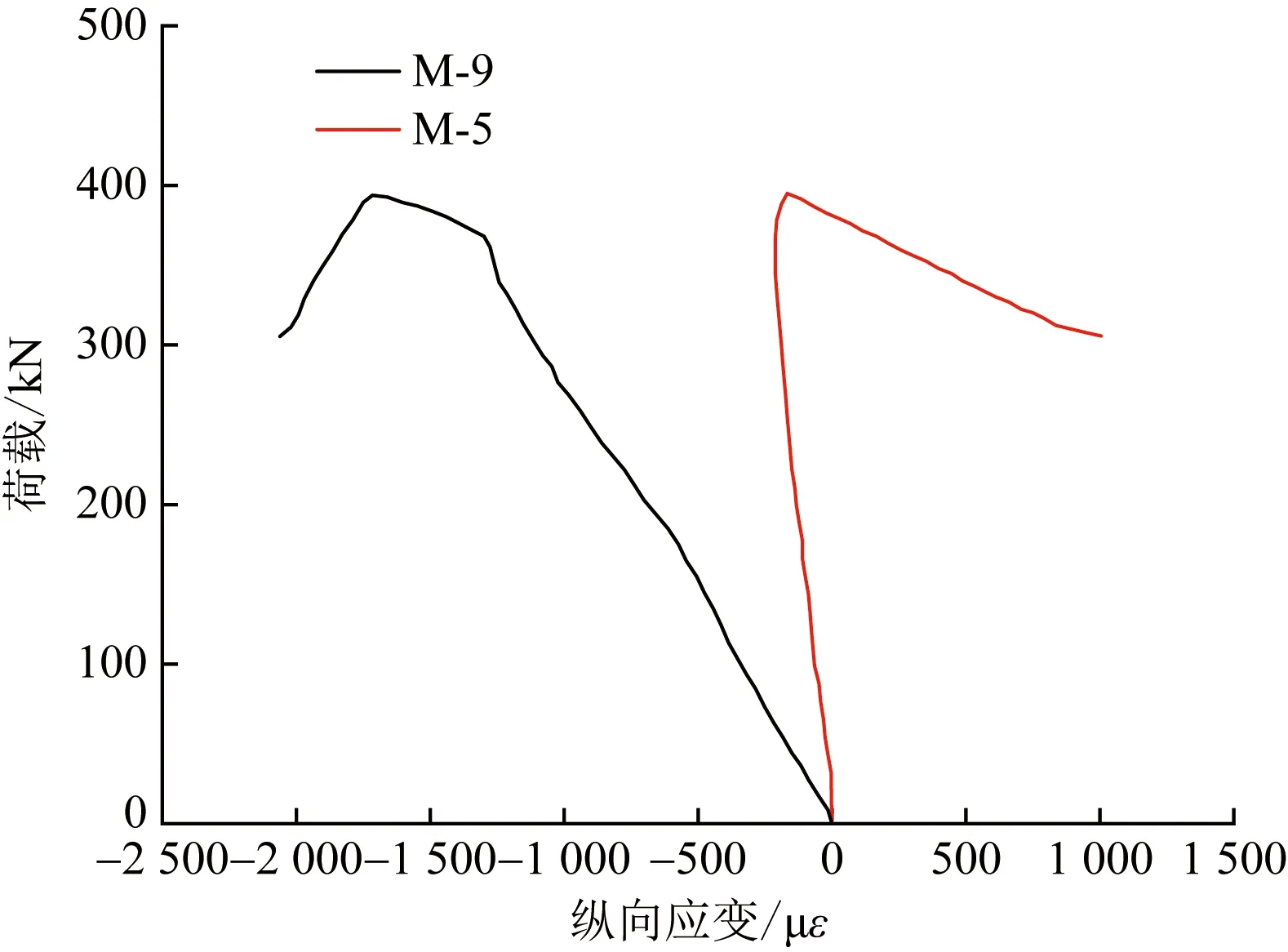
图7 Z-1C20D试件荷载与钢柱中部纵向应变关系图Fig.7 The relationship between the load of the Z-1C20D specimen and the longitudinal strain in the middle of the steel column

1.3.2 CFRP布纵向应变

图8为Z-1C20D试件中部受压应变情况，其他试件的应变曲线大致相同。图8中MC-3应变片为弯曲外侧，MC-4应变片为弯曲内侧。MC-3应变片在开始阶段受压，随着柱中侧移的不断增加，MC-3应变片由受压状态转变为受拉状态。当H型钢柱承载能力达到极限时，MC-3应变片的变形迅速增加。MC-4应变片始终处于受压阶段，在荷载达到极限承载力时，弯曲内侧的CFRP布开始发生褶皱或剥离，因此MC-4应变片在压力达到最大值后其压力值会保持稳定，不会出现压力下降的情况。对比钢柱纵向应变曲线和CFRP布纵向应变曲线发现在H型钢柱失稳破坏之前，CFRP布与钢柱粘接紧密，协同变形。

图8 Z-1C20D试件荷载与钢柱中部碳纤维布纵向应变关系图Fig.8 The relationship between the load of the Z-1C20D specimen and the longitudinal strain of the carbon fiber cloth in the middle of the steel column

1.3.3 偏心距对CFRP加固H型钢柱的影响

图9为在相同层数CFRP布加固的情况下不同偏心距对试件承载力的影响对比图。由图9可知，偏心距为10 mm的H型钢柱承载力高于偏心距为20 mm的H型钢柱承载力。偏心距为10 mm的H型钢柱在达到极限承载力时的位移大于偏心距为20 mm的H型钢柱。

图9 相同层数CFRP布试件所受荷载和柱中侧向位移变化关系Fig.9 The relationship between the load and the lateral displacement of the column with the same number of layers of CFRP cloth specimens

1.3.4 CFRP布层数对柱中侧向位移的影响

由图10可知，随着CFRP层数的增加，钢柱的承载力也在不断提升。观察上图不同曲线的斜率可以发现CFRP布层数越多斜率越大，说明试件经过CFRP布加固后可以提高一定的抗弯能力，延缓试件的侧向变形。

图10 相同偏心距下不同层数CFRP布加固试件所受荷载和柱中侧向位移变化关系Fig.10 The relationship between the load and the lateral displacement of the column under the same eccentricity of different layers of CFRP cloth reinforced specimens

1.3.5 试件极限承载力试验结果

通过图11可以看出，在偏心距相同的情况下，随着CFRP层数不断增加相应的承载能力也随之不断提升。但CFRP层数的增加和承载力的提升并非线性关系，此外CFRP布对偏心距较大试件的加固效果明显强于偏心距较小的试件。由表4可知随着偏心距的增大，试件极限时跨中挠度将会减小。

图11 CFRP加固试件承载力能力提升百分比Fig.11 Percentage increase in bearing capacity of CFRP reinforced specimens

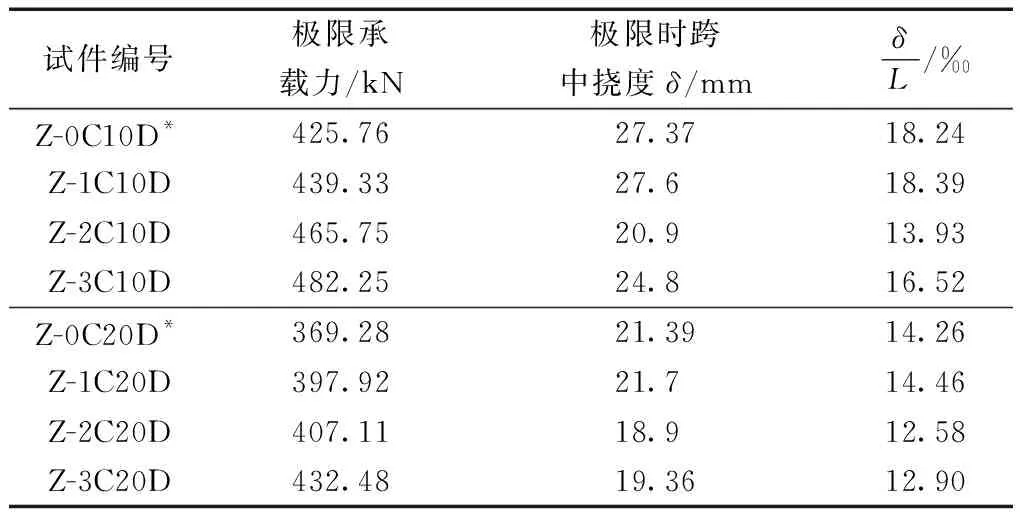
表4 各试件承载力试验结果Table 4 Test results of the bearing capacity of each specimen

2 理论分析和计算方法

钢结构具有强度高、材质均匀和塑性、韧性好等特点，因此现在很多建筑都采用钢结构作为其主体结构形式。但当钢结构的构件长细比过大或者受到很大的偏心荷载时，构件会出现失稳破坏的现象。

《钢结构设计标准》[14]中规定，轴心受压构件的稳定性计算公式为

(1)

式(1)中：N为轴压力；φ为轴心受压构件的稳定系数；A为构件的截面面积；f为钢材的抗压强度设计值。

构件的长细比可按下列公式计算：

(2)

式(2)中：λx、λy分别为构件绕截面主轴x、y的长细比；lox，loy分别为构件对截面主轴x、y的计算长度；ix、iy分别为构件截面对主轴x、y的回转半径。

将加固材料对应的纯钢材截面和原构件截面叠加[式(5)]，计算碳纤维加固后碳布等效面积与被加固构件组合而成的新纯钢构件的几何尺寸，然后计算新构件的长细比，查出加固后构件的稳定系数，将所有参数代入式(15)中验算其承载力，具体计算过程如下：

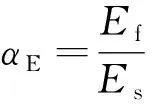
(3)

EsAt=EsAs+EfAf

(4)

(5)

式中：αE为CFRP加固材料弹性模量与被加固钢材弹性模量的比值；Es为钢材的弹性模量；Ef为碳纤维加固材料的弹性模量；At为构件加固处理后对应的纯钢截面面积；As为需加固构件的原截面面积；Af为碳纤维加固材料的截面面积。

复合截面惯性矩的计算也按以上叠加原理进行：

EsIt=EsIs+EfIf

(6)

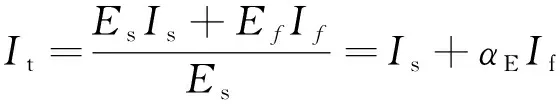
(7)

式(6)中：It为加固后的构件对应纯钢截面惯性矩；Is为被加固构件初始截面惯性矩；If为CFRP材料截面惯性矩。

直观上看：式(5)中αE放大的是面积，式(7)中αE放大的是惯性矩。但同一个αE不会放大两个不同单位的物理量，下面证明αE放大的是碳布垂直于弯矩作用平面方向(x轴)的长度。

CFRP布加固H型钢柱如图12所示。图12中左上方蓝色框中的CFRP截面详见图13，图12中右上方蓝色框中的CFRP截面详见图14。

红色部分为碳纤维布；黑色部分为H型钢柱；M为垂直于平面绕x轴弯矩图12 CFRP布加固H型钢柱Fig.12 CFRP cloth reinforced H-shaped steel column

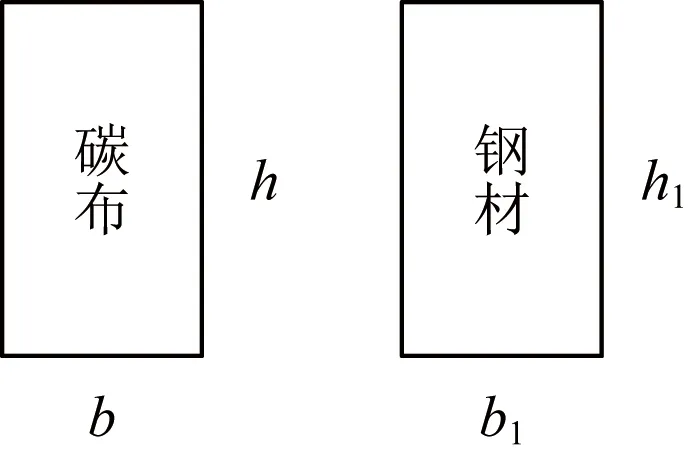
图13 碳布截面示意图Fig.13 Schematic diagram of cross section of carbon cloth

图14 碳布截面示意图Fig.14 Schematic diagram of cross section of carbon cloth

假设x轴为水平方向，被加固的钢材面积As=0，碳纤维布截面为长方形截面宽为b、高为h， 碳纤维布转换成钢材后钢材的截面宽为b1、高为h1(图13)。

由式(5)得

b1h1=αEbh

(8)

由式(7)得

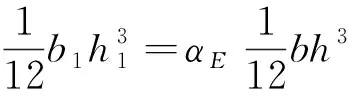
(9)

将式(8)代入式(9)化简得

h1=h

(10)

式(10)说明碳纤维布换算成钢材是在其厚度b方向(即x轴方向)乘以增大系数，在长度h方向上等效为钢材后碳纤维布的长度不变。

碳纤维布横放(图14)按上述思路重新推导。

由式(5)得

h1b1=αEhb

(11)

由式(7)得

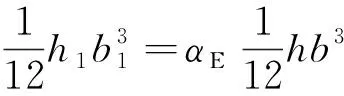
(12)

将式(11)代入式(12)化简得

b1=b

(13)

式(13)说明碳纤维布换算成钢材是在其长度h方向(即x轴方向)乘以增大系数，在宽度b方向上等效为钢材后碳纤维布的宽度不变。

通过上面推导证明碳纤维布面积换算为钢材面积时，是将碳布垂直于弯矩作用平面方向的长度乘以放大系数进行计算，并非直接放大碳纤维布的面积或是惯性矩。

将式(5)和式(7)代入式(2)中得

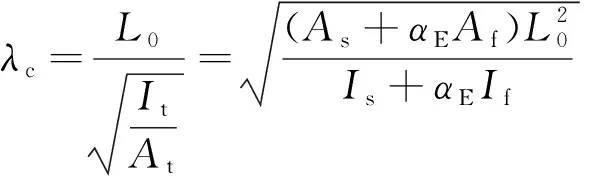
(14)

式(14)中：λc为加固后构件的长细比；L0为加固后构件的有效计算长度。

查出加固后构件稳定系数后，通过式(15)计算构件的极限稳定承载力：

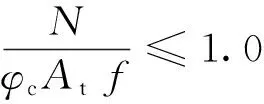
(15)

式(15)中：N为加固后构件的极限稳定承载力；φc为加固后构件的稳定系数。

《钢结构设计标准》[14]给出了实腹式压弯构件(包括偏心受压构件)稳定问题有关的计算公式。本文研究采用的计算公式[式(16)]推导过程同上。式(16)中与截面尺寸有关的变量均为碳布加固后等代换算的新纯钢构件的截面尺寸。

(16)

3 结果对比

试验采用的CFRP布每层厚度均为0.167 mm，黏接的结构胶每层厚度为0.2 mm。将相关参数代入式(16)计算，可得出极限承载力的理论计算值，如表5所示。

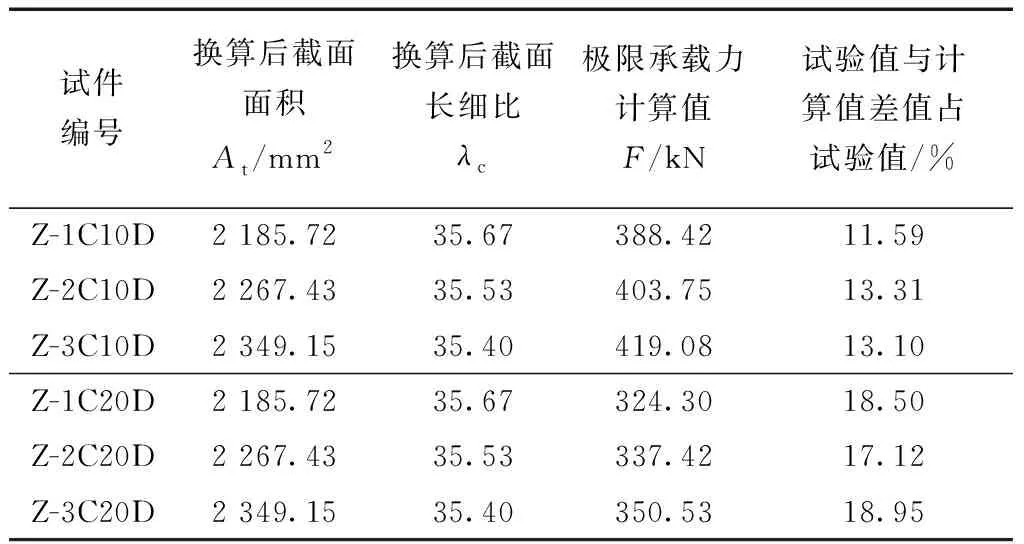
表5 试件极限承载力计算值与试验值对比分析Table 5 Comparative analysis of the calculated value and the test value of the ultimate bearing capacity of the specimen

通过表5可以看出，偏心距为10 mm时计算值与试验值的误差稳定在13%左右，偏心距为20 mm时计算值与试验值的误差稳定在18%左右。通过误差可以看出采用式(16)计算时不同CFRP层数不会改变计算结果的误差大小，而不同偏心距则会改变式(16)计算结果的误差大小。钢柱失稳时截面塑性发展情况，试验偶然误差，偏心距和胶层粘接强度等都会对试验结果产生影响从而导致计算值与试验值产生误差。式(16)是以《钢结构设计标准》的公式为基础推导而来，因此其计算结果相对较为保守，计算的极限承载力值相对于试验值偏小属于正常情况。

4 结论

通过6组CFRP布加固H型钢柱的偏压试验和理论推导对比分析得出以下结论。

(1)CFRP布加固偏压H型钢柱(以所选H钢柱试件尺寸为例)在偏心距为10 mm时1层、2层和3层CFRP对试件承载能力提升幅度分别为3.19%、9.39%和13.27%。在偏心距为20 mm时1层、2层和3层CFRP对试件承载能力提升幅度分别为7.76%、10.24%和17.11%。

(2)CFRP布加固偏压H型钢柱(以所选H钢柱试件尺寸为例)在偏心距为20 mm时比偏心距为10 mm时加固效果更好。

(3)H型钢柱发生失稳破坏时CFRP布会与钢柱剥离或者发生褶皱，考虑到CFRP布抗拉强度较高以及结构胶粘接性能不足(结构胶每层厚度为0.2 mm)的原因，故认为本次试验中H型钢柱发生失稳破坏时CFRP布的抗拉性能并没有完全发挥。

(4)以《钢结构设计标准》的公式为基础创新的采用面积代换的思想推导CFRP加固钢柱承载力的计算公式具有一定的借鉴意义。本次试验中，在荷载偏心距为10 mm时计算值与试验值的误差稳定在13%左右，在荷载偏心距为20 mm时计算值与试验值的误差稳定在18%左右。误差较为稳定证明了公式计算值较为合理，也说明了此公式若经过系数修正后其计算结果与真实值的离散程度会较小，误差产生的原因有很多，本次试验中其主要原因是理论计算并未考虑试件初始缺陷、理论计算假定H型钢柱两端为纯铰接状态、未考虑结构胶对承载能力提升的贡献和其他因素，因此计算值偏于保守。