小样本类不平衡数据的一致性分析流特征选择
2021-11-22林培榕曾海亮王晨曦林耀进
林培榕,曾海亮,王晨曦,卢 舜,林耀进
(闽南师范大学 计算机学院,福建 漳州 363000)
(数据科学与智能应用福建省高等学校重点实验室,福建 漳州 363000)
1 引 言
在语义分析[1]、人脸识别[2]、基因检测[3]等应用研究领域,产生了海量高维小样本数据.此类数据的特点主要表现为数据的样本数比起特征维度数少了一个量级以上.当前,面向高维小样本数据的分类学习任务存在着样本类别分布偏斜问题,即数据中至少一个类别代表了样本很少的数量,而其它类别的样本组成了大多数.特征选择是数据分类学习过程中重要的预处理技术.传统的特征选择技术倾向于学习大类而忽略小类,而在实际应用中,人们往往更关注小类样本的分类正确与否[4].例如,医疗诊断中因漏诊而判断为假阴性的代价比误诊为假阳性的代价更高;安全检测中漏检掉一个携带炸弹上飞机的恐怖分子要比搜查一个无辜的人代价大得多.因此,针对类别不平衡问题设计能正确识别小类样本的分类模型具有重要意义.此外,随着大数据技术的蓬勃发展,数据的形态日新月异.在真实场景中,作为动态数据的一种表现形态,数据流广泛存在于动态监测[5]、社交网络[6]和标签推荐[7]等领域.例如,在火星陨石坑检测中动态提取纹理特征;新浪微博热门话题的出现通常伴随着新关键词的产生.数据流蕴含的知识是时间的函数,由于数据的动态性和演化性,必然导致已有的学习模型带有滞后性.因此,设计具有实时性功能的学习模型已是迫在眉睫[8].
当数据的特征空间动态变化,传统的特征选择算法在流知识学习中显得捉襟见肘[9,10].为此,研究人员提出了许多在线流特征选择算法[11-16].文献[11]提出了一种基于逐步回归的在线特征选择算法,但该算法需要根据预知的候选特征构成来对初始特征进行变换;为了弥补上述算法的不足,文献[12]提出了流特征的概念,基于流特征设计了可以直接对初始特征进行处理的在线特征选择框架,并给出了两个有效的在线算法;文献[13]通过对特征之间两两相关的界限进行理论分析,提出了一个随时间变化的简约模型;文献[14]以特征组的方式对上述算法进行扩展,提出了在特征与特征组上稀疏的分组在线特征选择算法.然而,面向高维小样本数据的在线分类学习算法中依然存在着类别不平衡问题.于是,文献[15]针对小类样本重新定义邻域粗糙集下近似公式和依赖度公式,提出了基于特征和标记之间依赖关系的在线特征选择算法,旨在处理流特征环境下的类不平衡问题;文献[16]对上述算法进一步改进邻域粗糙集的下近似算子,运用了基于小类依赖度的在线特征选择模型.
在很多实际场景中,数据的特征空间具有动态性和演化性,主要表现为随着时间的流逝新的特征不断地流入数据的特征空间,导致传统的特征选择算法失效.在高维小样本在线分类学习任务中,若数据中样本的类别分布倾斜得十分厉害,那么无论在线分类学习算法选择什么样的特征,分类器只要简单地将所有样本都标记为大类,依然可以获得很高的预测精度.然而,却忽略了至关重要的小类样本,失去了实际意义[17].此外,有些在线分类学习算法[16]倾向于将数据中某一类别的样本设置成小类样本,而其余类别的样本全部设置成大类样本,人为地设置数据的大类样本和小类样本,该方法具有一定主观性,无法准确地体现出数据的复杂性与多样性.
从认知角度出发,样本在论域空间的分布是由特征决定的,分离性高的特征应使样本的分布在类内分散度尽量小,类间分散度尽量大.基于此,选择重要的特征更有利于分类.基于最近邻思想,相同特征空间下越相近的样本其类别往往越一致.于是,本文通过定义样本一致性概念来设计高维小样本类不平衡数据在线流特征选择算法.首先,利用均值定义同类样本的类中心,通过样本在特征与标记类别的信息定义类中心的近邻.其次,针对类别不平衡问题构建高维小样本一致性分析度量模型.再次,设计流特征环境下的高维小样本类不平衡数据在线特征选择算法;最后,实验验证所提算法的有效性.
综上,本文内容安排如下:第2节构建小样本类不平衡数据的一致性分析度量模型;第3节设计流特征环境下的类不平衡一致性分析的在线特征选择算法;第4节对算法进行实验验证与结果分析;第5节总结全文.
2 一致性分析度量模型
在真实场景中,类不平衡数据的样本类别呈现多类及类别分布偏斜等特点,其中数量较少的小类样本在众多样本中占据着举足轻重的地位,准确识别出类不平衡数据中的小类样本面临着严峻挑战.为此,本节简单介绍由特定特征诱导出的样本分布与标记的一致性概念来进行的特征选择[18].首先,利用均值定义同类样本的类中心;其次,基于特征空间的样本距离定义类中心的近邻,并根据类中心所在类别的样本数量定义近邻的大小;最后,定义近邻空间内样本类别和类中心类别一致的近邻样本与论域中和类中心同类的样本的数量比例为包含度.包含度反映特征对样本的区分与标记对样本的区分的一致性,不存在无法判断小类样本的情况.
定义1.定义决策系统〈U,F,L〉,样本集合U={x1,x2,…,xn},特征空间F={f1,f2,…,fm},标记L={X1,X2,…,Xc}将样本集合U划分成c个类别.对于∀Xj⊆L,nj是第j类样本的数量,∀xi∈Xj,定义Xj在特定特征空间条件下的类中心为:
(1)

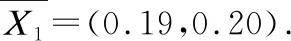
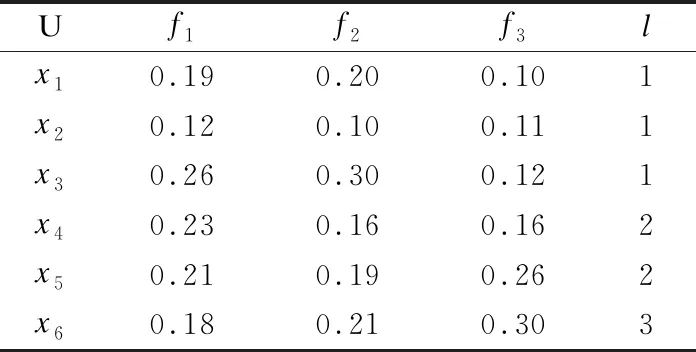
表1 小样本类不平衡数据示例表

(2)
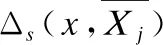

图1 同类样本类中心的近邻
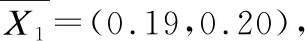

(3)

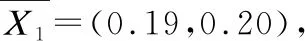

(4)
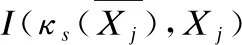

3 类不平衡一致性分析的在线特征选择算法
在很多实际应用中,数据的特征空间具有动态性和演化性,使需要提前获取数据全部特征空间的分类算法面临着功能滞后的风险.为此,本节将构建流特征环境下的小样本类不平衡数据的一致性分析在线流特征选择模型,并设计一种特征依次有序逐个流入决策系统的在线特征选择算法.首先,定义流特征决策系统数据特征的在线相关性分析;其次,定义流特征决策系统数据特征的在线冗余性分析;最后,提出类不平衡一致性分析的在线特征选择算法.
定义5.假设有流特征决策系统
CONf∪ft(L)>CONf(L)
(5)
CONf∪ft(L)表示t时刻决策系统特征空间中任意特征f与新特征ft联合一致性值,CONf(L)表示t时刻决策系统特征空间中任意特征f的一致性值,若式(5)成立,说明在t时刻到达决策系统的新特征ft与标记高度相关.此时,将新特征ft加入流特征决策系统,启动冗余性分析,否则,丢弃新特征ft,相关性分析挂起,继续等待新特征到达决策系统.
定义6.假设有流特征决策系统
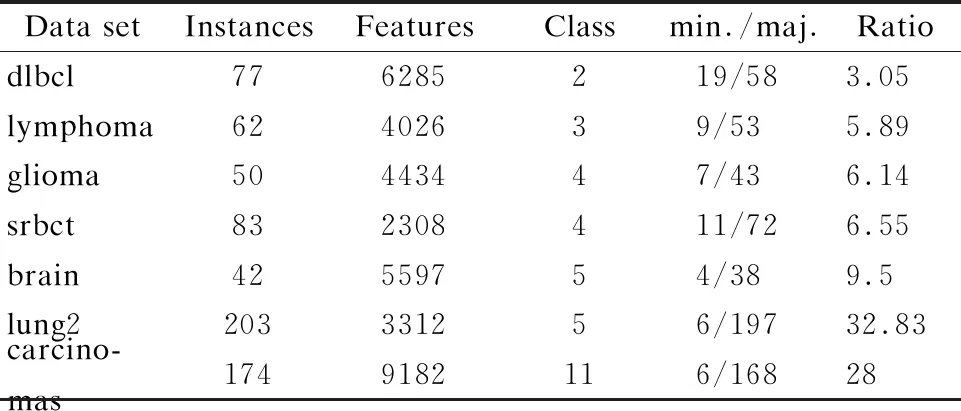
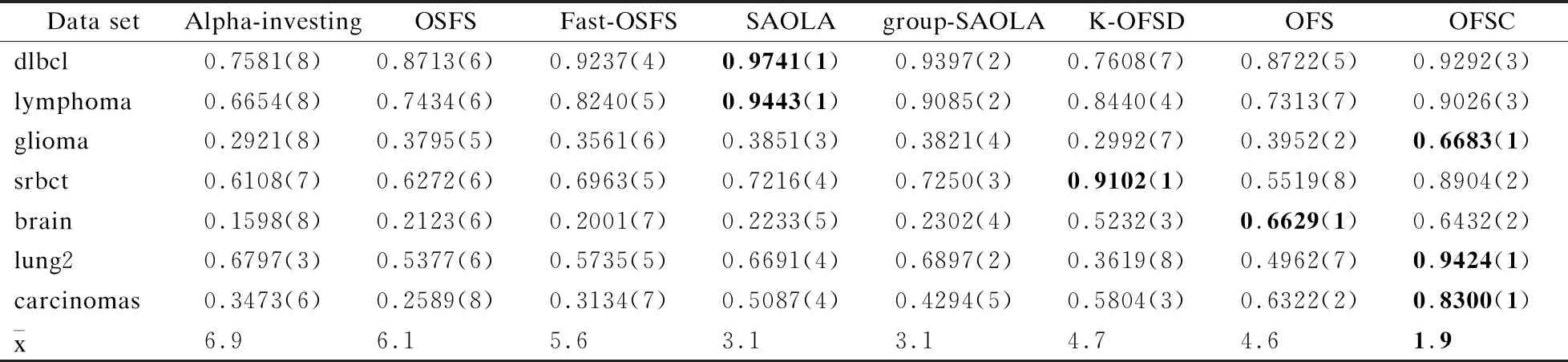
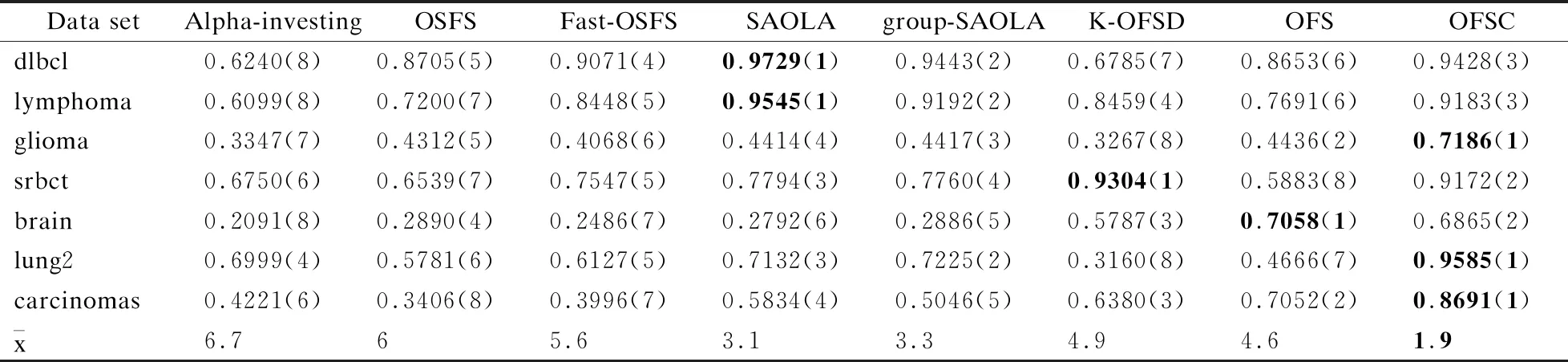
CONf∪ft(L) (6) CONf∪ft(L)表示t时刻决策系统特征空间中任意特征f与ft联合一致性值,CONft(L)表示在t时刻到达并流入决策系统的新特征ft的一致性值,若式(6)成立,说明t时刻决策系统中的特征f因新特征ft加入变成了冗余特征.此时,将特征f从决策系统的特征空间中删除.当t时刻决策系统中不再有冗余特征时,冗余性分析挂起,等待新特征流入决策系统. 根据定义5和定义6对流特征决策系统中的特征空间进行相关性分析和冗余性分析,可以有效丢弃冗余、噪声,以及不相关特征,从而选择出当前时刻流特征决策系统中的最优特征子集.基于此,本文将利用一致性度量模型构建一种流特征环境下的在线相关性分析与在线冗余性分析算法.该算法假定流特征决策系统初始特征空间为空集,新特征依次有序逐个流入决策系统.首先,当t时刻有新特征到达决策系统,触发相关性分析,启动相关性分析过程;其次,若新到达的特征流入决策系统,则触发冗余性分析,启动冗余性分析过程;最后,算法挂起,继续等待新特征到达系统.由此可见,流特征决策系统实时保持着最优特征子集. 根据以上分析,类不平衡一致性分析的在线特征选择算法具体描述如算法1所示. 算法1.类不平衡一致性分析的在线特征选择算法 (Online Feature Selection algorithm for Consistency analysis of class-imbalance,简称OFSC) 输入:流特征决策系统 输出:t时刻流特征决策系统的最优特征子集Ft 1.Ø→Ft/*特征空间初始为空集*/ 2.while(true) /*算法挂起,等待新特征到达系统*/ 3. ifftarrive /*t时刻ft到达,触发相关性分析*/ 4. ifFt=Ø 5.Ft=Ft∪ft/*第一个特征直接加入系统*/ 6. else 7. ∀f∈Ft/*t时刻系统Ft中的任意特征*/ 8. ifCONf∪ft(L)>CONf(L) /*相关性分析*/ 9.Ft=Ft∪ft/*ft流入,触发冗余性分析*/ 10. ifCONf∪ft(L) 11.Ft=Ft-f/*删除系统的冗余特征*/ 12. end if /*完成冗余性分析*/ 13. end if /*完成相关性分析*/ 14. end if 15. end if 16.end while 算法1中第1步表示初始特征空间为空集,新特征依次有序到达系统;第2步和第16步表示系统等待新特征到达;第3-15步表示当新特征到达系统时启动在线相关性分析,完成相关性分析后,若新到达的特征符合条件流入决策系统,则启动在线冗余性分析,其中,第一个特征到达时直接加入系统,不作相关性分析与冗余性分析.假设流特征决策系统标记有c个类别,在t时刻特征空间Ft有f个特征,则该算法的时间复杂度为O(c·f2). 为了验证OFSC算法的有效性,选取7个高维小样本类不平衡数据进行实验,分别为漫大B细胞淋巴瘤(dlbcl)、淋巴瘤(lymphoma)、小圆蓝细胞瘤(srbct)、胶质瘤(glioma)、脑(brain)、肺二(lung2)、肿瘤(carcinomas),详见表2[15]. 表2 小样本类不平衡数据集 1)漫大B细胞淋巴瘤包含2个类别共77例样本,分为19和58例,每例均由6285个基因组成. 2)淋巴瘤包含3个类别共62例样本,分为9、11和42例,每例均由4026个基因组成. 3)胶质瘤包含4个类别共50例样本,分为7、14、14和15例,每例均由4434个基因组成. 4)小圆蓝细胞瘤包含4个类别共83例样本,分为11、18、25和29例,每例均由2308个基因组成. 5)脑包含5个类别共42例样本,分为4、8、10、10和10例,每例均由5597个基因组成[19]. 6)肺二包含5个类别共203例样本,分为6、17、20、21和139例,每例均由3312个基因组成. 7)肿瘤包含11个类别共174例样本,分为6、7、8、11、12、14、14、23、26、26和27例,每例均由9182个基因组成. 如表2所示,数据集的特征空间是静态的,为了仿真流特征,算法设定数据集的特征空间是未知的,并且特征从第一个开始依次有序逐个到达流特征决策系统,当最后一个特征到达流特征决策系统完成在线分析时,算法挂起,表示当前没有新特征到达. 分类精度是分类学习算法最常用的评价指标,然而,在类不平衡数据分类学习任务中,无法识别小类样本的算法依然可以有很高的精度.因此,本文采用F-Score、G-Mean、分类精度和弗里德曼统计量综合评价算法的分类性能,其中,F-Score和G-Mean是两个评价算法对于类不平衡数据集分类性能的重要指标,弗里德曼检验则统计分析所有算法的性能. 关于F-Score和G-Mean评价指标的正负例样本的划分,本章算法采用依次遍历数据的样本类别.假设当前遍历到的类别为正类,则其余类别为负类,属于正类的样本为正例样本,属于负类的样本为负例样本.然后分别求各类别的F-Score值和G-Mean值,再求均值作为最终的F-Score值和G-Mean值. 设TP为真正例,TN为真负例,FP为假正例,FN为假负例,则查准率为P=TP/(TP+FP),查全率为R=TP/(TP+FN),F-Score定义为: (7) G-Mean定义为: (8) 为了显示算法的统计显著性,使用基于算法排序的Friedman检验,假定在N个数据集上比较k个算法,令ri表示第i个算法的平均序值,定义Friedman统计量为: (9) 其中, (10) 若“所有算法的性能相同”的假设被拒绝,则表明算法的性能显著不同,此时以Nemenyi后续检验进一步区分,Nemenyi检验计算出平均序值差别的临界值域为: (11) 本文实验全部运行在3.10GHz处理器,4.00GB内存,windows7系统和Matlab2013的实验平台上.为了避免数据特征因量纲不一致干扰实验过程,采用离差标准化将所有数据的特征值归一化到数值[0,1]区间. 多分类数据的类别存在对立的关系,只要类别足够多样,某一类样本对其余类全部样本来说即可视为小类样本,假设此类样本为正类样本,其余类样本即可统一视为负类样本.同理,遍历其余类别样本亦如此. 为了检验在线算法OFSC的有效性,选用Alpha-investing[11]、OSFS[12]、Fast-OSFS[12]、SAOLA[13]、group-SAOLA[14]、K-OFSD[15]、OFS[16]在线特征选择算法作为对比算法.其中,K-OFSD和OFS为面向高维小样本类不平衡数据的在线特征选择算法. 基分类器采用高斯核函数支持向量机RBF-SVM,验证方式采用5折交叉验证.因为数据集均为数值型数据,由文献[20]可知,算法OSFS、Fast-OSFS、SAOLA、group-SAOLA采用Fisher′s Z test度量方法,显著性水平的参数α=0.01,其中,算法group-SAOLA中的group=5.由文献[15]可知,算法K-OFSD的近邻参数k=7,特征与标记的相关性阈值β=0.5,以类别包含数量最少的样本为小类.由文献[16]可知,算法OFS中的近邻参数k=7,特征与标记的相关性阈值β=0.5,n=4,以类别包含数量最少的样本为小类. 4.4.1 预测精度分析 1)关于实验数据表的说明 实验数据表3-表5分别给出了各算法在各数据集上特征选择子集的平均F-Score值与算法比较序值表、平均G-Mean值与算法比较序值表,以及平均分类精度和标准差与分类精度的算法比较序值表.其中,圆括弧内的值为算法的比较序值,末行为算法在数据集上的平均序值,加粗部分的数据代表该算法在此数据集上的性能最优. 2)算法OFSC与对比算法的比较情况 由表3-表5可见,在数据集glioma、lung2、carcinomas上算法OFSC的分类性能均优于对比算法.在数据集dlbcl、lymphoma上算法OFSC的分类性能逊于算法SAOLA、group-SAOLA.在数据集srbct上算法OFSC的分类性能逊于算法K-OFSD.在数据集brain上算法OFSC的分类性能逊于算法OFS. 表3 平均F-Score值与算法比较序值表 表4 平均G-Mean值与算法比较序值表 表5 平均分类精度和标准差与算法比较序值表 3)算法OFSC与类不平衡算法的比较情况 易知,作为旨在处理类别不平衡问题的在线特征选择算法,OFSC只在数据集srbct上逊于对比算法K-OFSD,在数据集brain上逊于对比算法OFS,而在其它所选数据集上均优于面向类别不平衡问题的算法K-OFSD、OFS. 4)关于小类样本算法分类性能的结论 F-Score和G-Mean评价指标对于评价算法的小类样本分类性能的作用至关重要,OFSC算法在这两个评价指标上都获得了很高的值,由此可见,类不平衡一致性分析的在线流特征选择算法在处理高维小样本数据分类学习任务中的类别不平衡问题具有高效的表现能力. 4.4.2 统计性分析 1)计算评价指标的弗里德曼统计量 查找F检验参数alpha=0.05的常用临界值表可知,8个算法7个数据集的临界值为2.237,如表3-表5末行中算法的平均序值所示,由Friedman统计量公式计算出F-Score、G-Mean、分类精度的τF值分别为5.356、5.215、4,均大于F检验临界值2.237,因此拒绝“所有算法性能相同”的假设,进行Nemenyi后续检验.查找Nemenyi检验参数alpha=0.05的常用qα值表可知,8个比较算法的qα=3.031,由Nemenyi检验的临界值域公式得到临界值域CD=3.969. 2)根据平均序值差距是否超出临界值域比较算法的性能 由表3和表4末行中的平均序值可知,算法OFSC与算法Alpha-investing、OSFS的差距超过了临界值域,说明算法OFSC显著优于算法Alpha-investing、OSFS.由表5末行中的平均序值可知,算法OFSC与算法Alpha-investing的差距超过了临界值域,说明算法OFSC显著优于算法Alpha-investing.而算法OFSC与其它算法的差距没有超过临界值域,说明它们没有显著差别. 3)绘制弗里德曼检验图描述算法性能的差异 上述分析可以直观地用Friedman检验图显示,图2(a)-图2(c)的Friedman检验图分别由表3-表5中的算法比较序值导出,横轴刻度表示平均序值,纵轴刻度表示算法,和表3表头的算法一一对应.其中,第8号直线表示算法OFSC的平均序值和临界值域.用圆点显示算法的平均序值,以圆点为中心的横线段表示算法临界值域的大小,若两个算法的横线段有交叠,说明这两个算法的分类性能没有显著差别,否则说明其性能有显著差别.由图2可见,图2(a)、图2(b)中直线8号算法OFSC与虚线1算法Alpha-investing、2号算法OSFS的横线段没有交叠区域,说明算法OFSC显著优于算法Alpha-investing、OSFS.子图c中直线8号算法OFSC与虚线1号算法Alpha-investing的横线段没有交叠区域,说明算法OFSC显著优于算法Alpha-investing.而算法OFSC与其它点划线算法的横线段有交叠区域,说明它们没有显著差别.显然,算法OFSC的平均序值均高于对比算法,说明OFSC的综合分类性能均优于对比算法. 图2 OFSC算法与对比算法的弗里德曼检验图 4.4.3 稳定性分析 为了验证算法的稳定性,绘制雷达图来表示多数据集多算法在评价指标上的稳定性指数.图3(a)-图3(c)分别给出了算法在F-Score、G-Mean和分类精度评价指标上的稳定性指数.其中,纯黑直线代表算法OFSC的稳定性值.由图3可见,OFSC在4个数据集上接近稳定解,在数据集brain、glioma上稳定性较弱. 图3 OFSC算法与对比算法的雷达图 鉴于大数据本身的动态特性,数据的初始特征集合可能是未知的,甚至可能是空的,随着数据流的到达而引入新的特征.此外,高维小样本中存在着类别不平衡问题在概念发生漂移情形下并没有消失.因此,本文以高维小样本类不平衡数据为研究内容,围绕数据分类学习过程中面临着大类覆盖小类的挑战,提出了在流特征环境下的小样本类不平衡数据的一致性分析在线特征选择算法.该算法利用均值定义了同类样本的类中心,并通过融合类别信息来定义类中心的近邻及其在特征空间的一致性,由此设计了流特征环境下的在线特征选择算法.虽然类中心的定义有效地加速了算法的计算过程,但是,模型只训练了类中心,导致学习模型训练不充分,分类精度有所下降,下一步工作可考虑加强学习模型训练的充分性.4 实验结果与分析
4.1 实验数据
4.2 评价指标
4.3 实验设置
4.4 实验分析



5 结束语
