改进自适应遗传算法在多载AGV调度的应用研究

刘 畅，张承瑞，孙玉玺

(山东大学 机械工程学院，济南 250061)

(山东大学 高效清洁机械制造教育部重点实验室，济南 250061)

1 引 言

随着工业4.0时代的智能工厂的引入，工厂规模越来越大，对自动导引运输车(Automated Guided Vehicle，AGV)的需求量变大，调度复杂性增加，AGV调度机制应该更加高效、鲁棒.

现在已经有很多学者对多AGV调度进行研究.Valerio Digani，M.Ani Hsieh等[1]提出一种优化策略，来最大化AGV的吞吐量；Bai Li，Hong Liu，Duo Xiao等人[2]提出一种集中式多AGV运动规划方法，计算效率更高.但是，国内外研究的多AGV路径规划问题大多数是基于单负载，对多负载AGV的研究较少.

Azimi等[3]较早的研究了多载AGV调度需要解决的问题.Ho Y-C，Chien S-H研究多负载AGV的相关问题[4]，并且重点研究了多负载AGV的提取分配原则[5].霍凯歌等[6]，已经对自动化集装箱码头中的多载AGV调度问题进行研究，他们发现，多载AGV比单载AGV效率更高.Li-xiang Zhang等[7]研究了在自动化汽车装配线环境下，多载AGV高效运输物料的问题，并使用遗传算法进行求解.Li-zhen Du等[8]研究了在纺织车间环境下，多载AGV运输物料的问题，并且使用混合遗传算法和粒子群算法进行求解.

随着任务的维数增加，传统算法求解的时间复杂度大.所以，国内外很多学者使用智能算法(如头脑风暴算法[9]、粒子群优化算法[10])来对多AGV调度问题进行求解.

上述论文中，大多只是简单的假设多载AGV运输1个或2个负载，只考虑负载重量的约束，却没有考虑负载的体积约束.

本文第2节描述多载AGV调度问题的环境，第3节对路径规划问题进行建模，第4节对初始数据进行预处理之后，使用改进的自适应遗传算法进行求解，第5节将改进的自适应与标准遗传算法和自适应遗传算法进行比较.

2 问题描述

对于工厂的物料运输问题，在传统的单载AGV模型中，不需要考虑体积、重量约束，只是将一种物料运输到目的地，一次只执行一个任务.这极大的浪费了AGV的负载能力.

如图1所示，AGV没有任务时，会停靠在充电区域(charge area)，进行充电或者待机.任务集合发布时，AGV从充电区域(charge area)来到仓库(warehouse).在不超过AGV体积、重量约束的条件下，根据调度算法求解得结果进行加载货物，然后正式开始运输货物.在图1的多载AGV运输物料示意图中，AGV可以根据任务需求自由地到达任意一点.当AGV负载为空时，会返回仓库(warehouse)进行下一个任务的运载.周而复始，直到所有任务完成后，AGV会回到充电区域进行充电或者待机，直到下一个任务集合的到来.

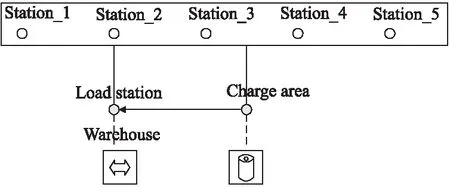
图1 多载AGV运输物料示意图

3 建立模型

本文主要解决的是工厂环境下如何高效调度多载AGV的问题.

3.1 符号说明与模型假设

符号说明

M：表示路径规划的路径数目；

Ni：表示在规划的第i路径中，执行任务点的数目；

cij：表示在规划的第i条路径中，从仓库出发到第j个任务点所产生的成本；

Gij：表示在规划的第i条路径中，第j个任务点所需要的物料的重量；

G：表示多载AGV可承受的最大重量；

Vij：表示在规划的第i条路径中，第j个任务点所需要的物料的体积；

V：表示多载AGV可承受的最大体积；

Aijk：表示第k个任务是否在第i条路径的第j个任务点被执行；

K：表示任务总数目；

d_list：表示只能被单个运输的任务点形成的路径；

dd_list：表示被最短路径模型求解后得到的路径集合；

p_list：表示d_list和dd_list两个集合的并集.

模型假设

1)单个任务的负载不会超过多载AGV的最大载重约束和体积约束；

2)AGV行驶单位长度，成本相同；

3)AGV匀速行驶.

3.2 调度模型

目标函数：

(1)

约束函数：

(2)

(3)

(4)

(5)

公式(1)为模型的目标函数，为距离函数矩阵，表示路径的成本；公式(2)为多载AGV的重量约束；公式(3)为多载AGV的体积约束；公式(4)、公式(5)，约束任务能且只能被一辆多载AGV完成.

4 改进的自适应遗传算法

遗传算法[11]实现简单，通用性强，易于和其它算法结合，具有并行性和鲁棒性.但是，它也存在过早收敛、局部搜索能力弱等问题.

针对标准遗传算法的上述不足，本文在自适应遗传算法的基础上，加入灾变操作与逆变操作，提出一种改进的自适应遗传算法(Improved Adaptive Genetic Algorithm，IAGA)，如图2所示，其为改进自适应遗传算法的流程图.

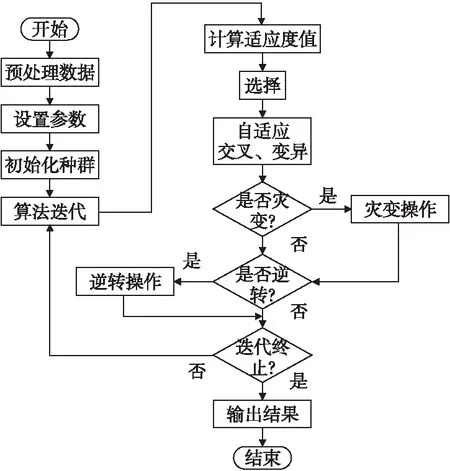
图2 IAGA流程图

在初始化种群后，算法进入迭代部分，进行选择、交叉、变异操作.

然后进入灾变操作，根据适应度值，求解灾变算子，判断是否执行灾变操作，灾变算子随着陷入局部极值迭代次数的增加，不断的增加种群的交叉概率和变异概率，使算法更容易跳出局部极值.

之后，进入逆转操作，即局部搜索部分.当满足逆转条件后，进入逆转操作.在逆转操作中，添加了倒序操作与插入操作.选取种群的部分染色体，根据倒序概率和插入概率，判断是否进行倒序操作或者插入操作，执行完毕后，将操作后的染色体的适应度值，与操作前的适应度进行比较.适应度值变大时，才会接受新解.算法将沿着适应度变高的方向进行进化.

最后根据迭代终止条件(迭代次数或者收敛)，判断是否终止迭代.

4.1 适应度函数

目标函数为最小路径.为了方便编程和简化智能算法的迭代过程，本文使用惩罚函数的方式，将重量的约束与体积约束，加入到成本函数中.适应度值为成本的倒数，成本越大，适应度越小.适当调整α，β的值，满足各个AGV的载重约束和体积约束.

(6)

(7)

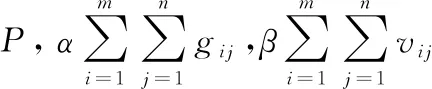
4.2 自适应策略

自适应交叉算子、变异算子

本文采取文献[11]中，正弦自适应遗传算法的遗传算子的求解公式.

(8)

(9)

其中，pc为交叉概率；pm为变异概率；pc1为种群的最大交叉概率；pc2为种群最小交叉概率；pm1为种群的最大变异概率；pm2为种群最小变异概率；fm为种群的最大适应度；fa为种群平均适应度；f′为染色体个体适应度；

自适应遗传算子随着适应度的变化而不断变化，可以很好地提高遗传算法的收敛速度和性能.

自适应灾变算子

传统的灾变算子是固定值，导致对每个算例的适应性不强，需要不断调整.

本文提出一种自适应灾变算子，它随着陷入局部极值的代数的增加，不断增加交叉概率与变异概率，使整个种群跳出局部最优解.

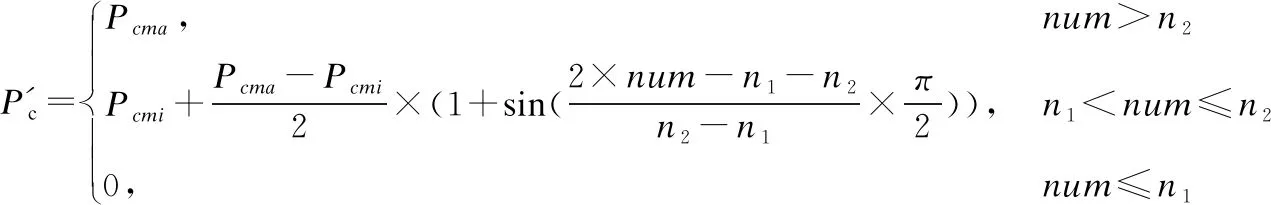
(10)

(11)

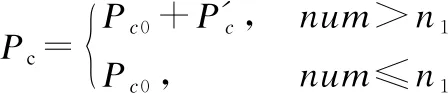
(12)

(13)

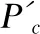
灾变算子的自适应调整，如图3所示，在算法迭代初期，种群适应度急剧变化阶段，不会发生作用.在种群陷入局部极值后，随着陷入极值的时间越长，灾变算子使得交叉概率和变异概率不断增大.

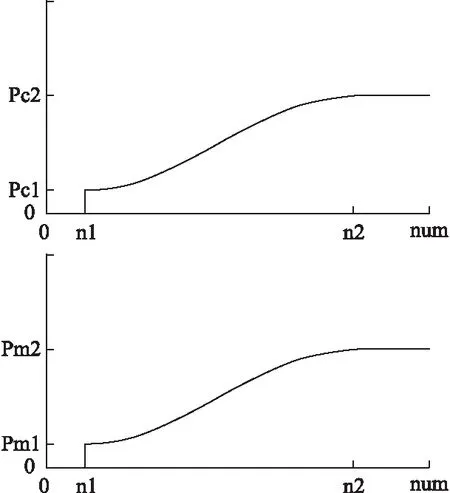
图3 灾变阶段交叉概率、变异概率变化量

自适应逆转算子

本文提出一种自适应逆转算子，随着总迭代次数的增加，逆转算子不断改变，使得种群进行逆转操作的概率增大.

(14)

其中，Pi为执行逆转操作概率；Pim为最大逆转概率；T为迭代周期；ite为迭代次数.

如图4所示，在算法的迭代初期，种群的多样性大，不需要过多的进行逆转操作.在算法的后期或者迭代陷入局部最优值时，适当的进行逆转操作，既可以增加种群的多样性，也有利于跳出局部极值.而且，逆转操作使得种群向着更加有利的方向进行进化，容易跳出局部极值.

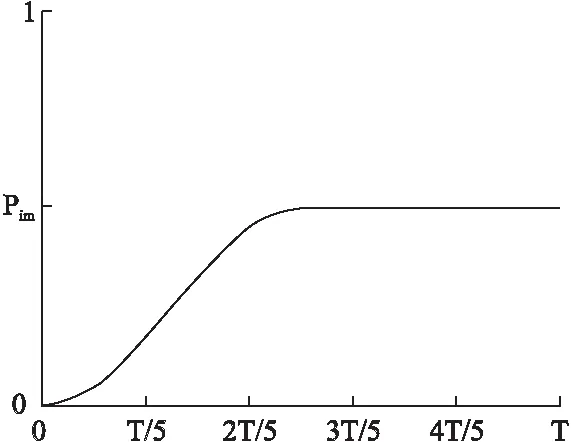
图4 逆转操作概率的自适应调整

4.3 算法基本流程

4.3.1 数据预处理

1)剔除重量大或者体积大的任务

分析所有任务点需要的物料的重量与体积，删除重量很大或者体积很大、无法与其他物料进行一起运输的物料订单.这样的物料只能单载运输.形成单载AGV路径集d_list.之后，智能算法求解多载AGV路径集合dd_list.

剔除重量大或者体积大的任务，将其组合成单独的任务队列，可以减少调度系统的搜索的维度，使得算法求解的效率更高，速度更快.

2)根据数据提供的x坐标与y坐标，计算直线距离，提前生成距离矩阵，避免在程序计算中重复计算，降低程序的计算量.

4.3.2 调度模型求解

编码与解码

采用实数编码的策略.常见的二进制编码虽然简单易行，不适合高维、高精度优化问题.这里采用实数编码.

仓库的编码：0，分割各个字符串.例如：任务点1-4为一组，6-9为一组，11-14为一组，编码后的染色体的编码字符串，1-2-3-4-0-6-7-8-9-0-11-12-13-14，这就是编码过程.解码过程则相反.

选择

本文采用轮盘赌选择方式.根据每个个体的适应度，按照比例进行概率选择.适应度越大的染色体被选中的概率越大，反之，适应度越小的染色体被选中的个体越小.

交叉、变异

采用两点交叉方式.随机选中小于染色体编码长度的两个数，将它与临近的染色体相同位置进行交换.但是由于采用的是实数编码.所以，交叉操作完成之后，相应的染色体内部，需要进行调整.

采用单点变异的方式.因本文采用的是实数编码，所以单点变异后，需要进行调整.

逆转

选出部分种群，根据设定好的概率(倒序概率，插入概率)，使用逆序排列，插入排列的方式，保留适应度值增大的染色体，否则恢复大原基因排列.这样做的目的，一是增加种群的多样性，二是可以向着种群适应度值高的方向进化.

调整

因采用实数编码，除0外的其他实数应保持数字的唯一性，当进行交叉变异等操作后，需要进行调整，来满足染色体数字的唯一性.

5 仿真验证

本文的实验环境为：Windows 10+MATLAB 2014b.本文的算例由Solomon[12]提出的算例调整修改而来，任务数据包括位置，重量约束，体积约束初始任务数据包括位置，重量约束，体积约束.搭建了一个仓库点，(N-1)个工作站，在共N个点的环境.多载AGV能承受负载的最大重量为4，多载AGV能承受负载的最大体积为4.

分别在N为30，60，90 3个规模下，各做10组实验，取得3种规模下，改进的自适应遗传(IAGA)，标准遗传算法(Standard Genetic Algorithm，SGA)，自适应遗传算法(Adaptive Genetic Algorithm，AGA)算法，3种算法收敛的迭代次数、迭代时间、迭代精度.

分析图5可知，在相同的迭代次数下，改进的自适应遗传算法比标准遗传算法、自适应遗传算法收敛速度更快、更加接近最优值.

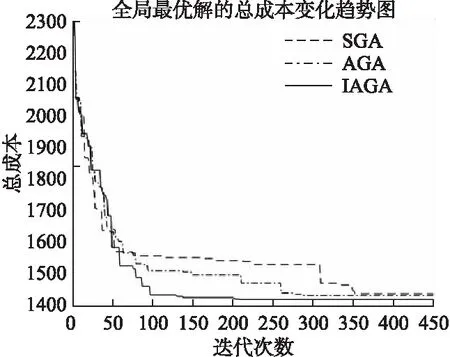
图5 N=30，各个算法迭代变化趋势

由表1-表3，比较3种算法在N=30，60，90维度下的的迭代次数、迭代时间、收敛解，可知，改进的自适应遗传算法迭代次数更少、达到收敛的时间更短，收敛解更加接近最优解.

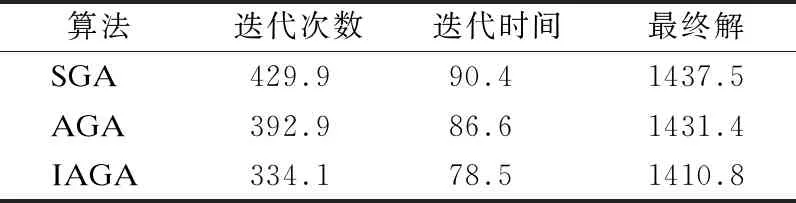
表1 N=30，各个算法比较

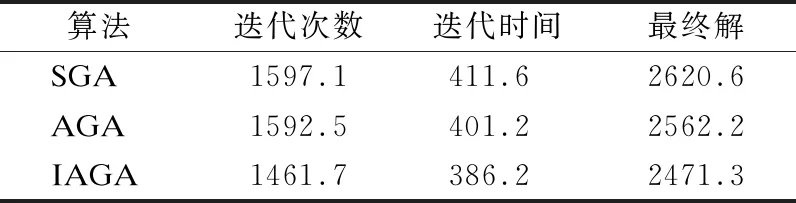
表2 N=60，各个算法比较

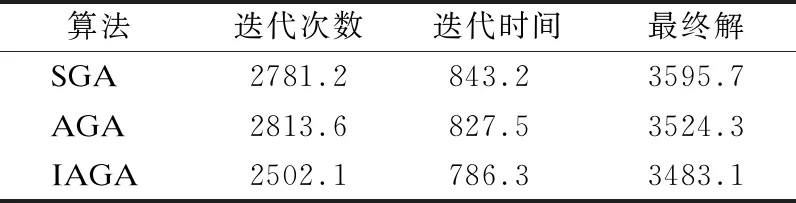
表3 N=90，各个算法比较

6 结 论

本文中，多载AGV调度问题是一个添加了物料体积、重量双重约束的VRP(Vehicle Routing Problem，车辆路径规划问题)问题.本文首先对数据进行预处理，降低求解变量的维度，然后使用改进的自适应遗传算法(IAGA)进行求解，最后，分别在数据维度N=30，60，90时，进行多组实验取平均值.与标准遗传算法(SGA)、自适应遗传算法(AGA)相比，改进的自适应遗传算法收敛快，优化效果明显，收敛精度高.

在求解过程中也发现一些不足：1)在任务合并寻优过程中，迭代时间长，可以进一步改进算法或者调整参数来进行加快收敛；2)本文没有考虑时间约束，在后续工作中可以加入时间窗约束.