基于典型代表电站和改进SVM的区域光伏功率短期预测方法

2021-11-20张扬科李秀峰

电力自动化设备 2021年11期

张扬科，李刚，李秀峰

（1. 大连理工大学水电与水信息研究所，辽宁大连 116024；2. 云南电力调度控制中心，云南昆明 650000）

0 引言

近年来，我国新能源代表之一的光伏产业发展迅猛，2019 年年底光伏电源装机容量达到2.04×108kW，同比增长17.3%。随着光伏渗透率的逐年提高，单站功率预测已无法满足调度部门协调调度以及国家对新能源消纳的迫切需求，亟需展开对区域光伏功率预测的研究。主要体现在以下几个方面：电网调度与电源规划方面，精确的区域功率预测有利于调度部门实现对大规模光伏电站的掌控以及减弱光伏并网对电网的冲击［1］，同时将光伏电源纳入多能源互补协调调度体系可提高多种能源之间的协同运作能力［2］；运行风险方面，单一光伏电站因发电随机性、波动性［3］无法顺利参与整体协同优化，而区域出力因汇聚效应可减少系统运行带来的风险，进而增强电网运行安全性；电力市场方面，2015 年国务院发布的《关于进一步深化电力体制改革的若干意见》［4］提出，允许拥有分布式电源的用户或微电网参与电力交易，而分布式电源因“就近建设”的特点更容易形成光伏汇聚区，因此区域预测对日内现货市场和电力交易具有重要意义［5］；模型适应性方面，单站预测模型需根据不同电站资料重新构建，这导致不同电站之间的模型无法共用，而由于相关性愈强的汇聚区彼此出力相互抵消的能力愈强，对区域出力波动起到“削峰填谷”的作用［6］，从而使总体出力趋势更加明显，降低了预测难度。

光伏功率预测一直是国内外研究的热点，按预测模型组成可分为3 类：物理成因法，根据光伏电站的组件参数和地理信息，如光电转换效率、光伏阵列的安装角度等，结合当地的气象信息，按光伏物理成因建立预测模型［7］；统计学法，对光伏出力数据、误差数据等历史数据进行统计和曲线拟合，寻找适合该类数据的函数或概率模型构建输入、输出映射关系，达到预测的目标［8］；人工智能算法，利用人工智能算法对历史资料进行处理，使输入、输出间形成非线性关系，进而得到预测结果［9］。由于汇聚区与单一电站功率预测在预测原理、数据资料的使用及建模方式方面的不同，区域功率预测无法“照搬”单站预测的形式。同时，由于多座单一电站的预测误差积累和数据量级的影响，区域功率的预测值无法直接采用多座单一电站预测值进行简单叠加。文献［1］使用系数矩阵将个别电站预测功率推算到区域功率，但该方法计算过程较为繁琐；文献［10］利用Pearson相关系数选择各汇聚区代表电站，但单一数学指标无法全方位分析该电站对汇聚区的代表性；文献［11］使用类似滚动预报方法进行功率预测，但传统滚动预报的误差随时间迅速增加，不是最优的预测方法。

为此，本文提出一种基于典型代表电站和改进支持向量机（SVM）的区域光伏功率短期预测方法。首先结合多种数据通过聚类分析形成不同的光伏汇聚区；然后引入3种相关系数选取各汇聚区中的典型代表电站，并通过4 类评价指标对汇聚区中各电站进行相关性分析；最后利用改进SVM 构建典型代表电站与汇聚区间的短期功率预测模型，通过典型代表电站功率预测得到汇聚区总的光伏功率。算例结果表明，该方法可提高区域光伏功率短期预测精度。

1 光伏汇聚区的建立

光伏汇聚区的划分不仅与出力有直接关系，同时与特性数据和气象数据等内在因素密不可分。文献［12］注重考虑气象因素和发电功率的聚类分析，但是没有考虑光伏出力的特性因素。

为使汇聚区中各电站在数据上更加体现集群内部电站特征趋同性，在单站出力数据的基础上，添加光伏出力的相关特性数据，即最大值、最小值、平均值、峰谷差、变异系数［13-14］和气象因素，进一步提高数据系列的独立性。光伏汇聚区划分示意图见图1。

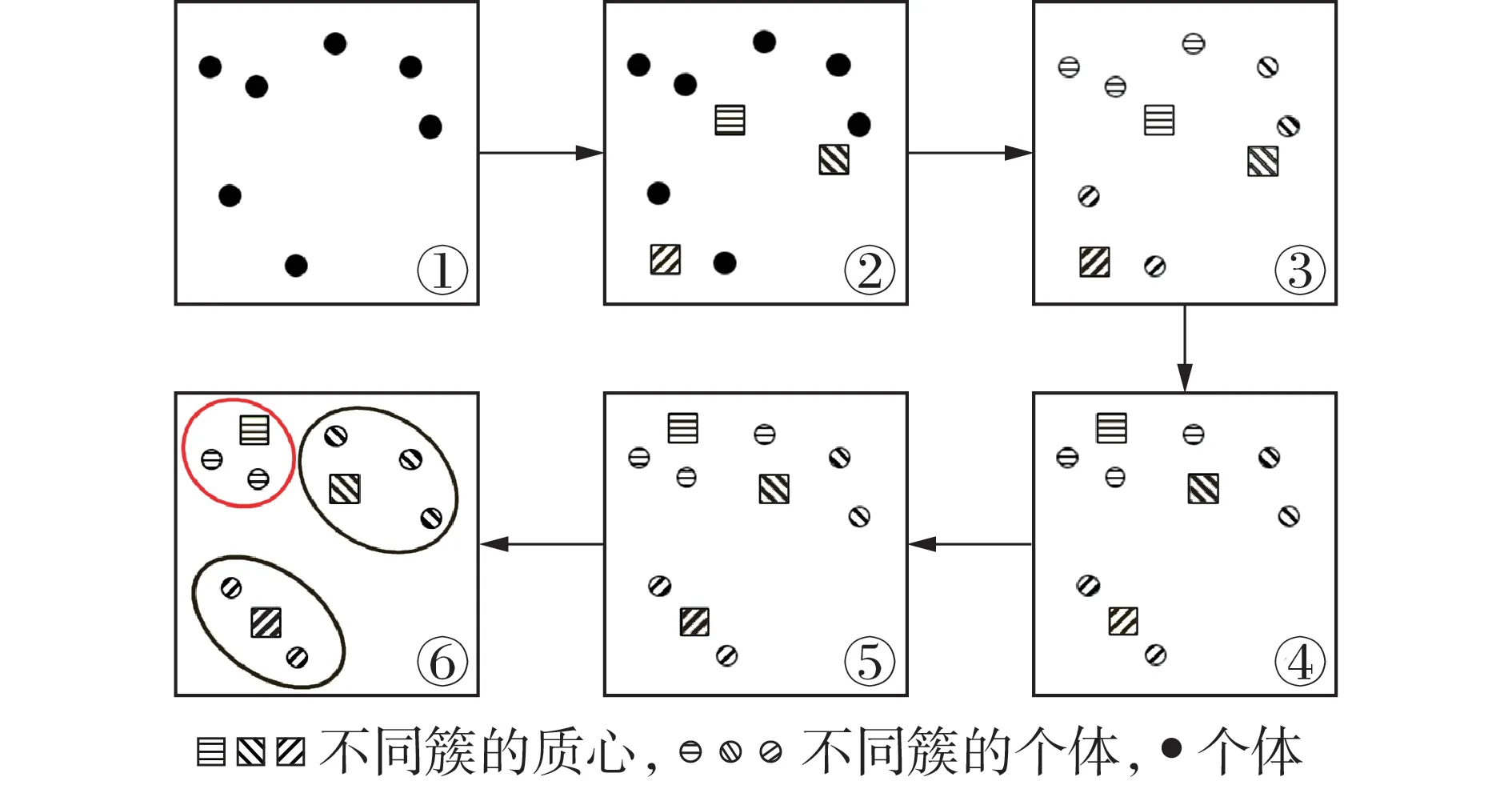
图1 汇聚区划分示意图Fig.1 Schematic diagram of convergence area division

利用K-means 聚类方法首先需要确定汇聚区的数量K，采用误差平方和最小作为评价函数：

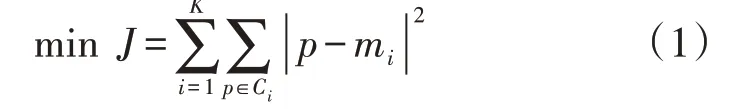
式中：J为各簇中个体与质心差的平方和；Ci为第i个簇；p为Ci中的样本；mi为Ci的质心，其为Ci中所有样本的均值。

如前文所述，将数据系列作为样本集合，通过迭代计算得出样本集合的K簇，主要计算步骤为：

1）输入样本集合M，随机选定K个点设为初始聚类中心，分别将其作为K个簇的中心，形成初始聚类结果，如图1中①—③所示；

2）更新各个簇的中心，计算任一簇中包含的所有样本数据对应的均值，将其设置为该簇的新中心，如图1中④所示；

3）计算每个样本与各簇中心的欧氏距离，将其分配到离其最近的簇，如图1中⑤所示；

4）判断是否满足迭代停止条件（达到循环次数或者误差平方和达到最小值等），若满足，则聚类完成，输出最终汇聚区划分结果，如图1 中⑥所示，否则，返回步骤2）。

利用上述步骤可以得到不同类别的划分结果以及对应评价函数的数值，将数值从大到小排列，找到下降速度最大的点，则该点数值对应的划分类别和聚类结果即为最终结果。

2 汇聚区典型代表电站的选取及相关性评价

根据上述方法将区域相关性较强的光伏电站划分到同一汇聚区，即区域中光伏电站的历史出力与质心（各电站出力均值）的距离越小，区域相关性越强，越易形成汇聚区。本文的关键点在于汇聚区典型代表电站的选取，但常用方法［10］仅关注Pearson 相关系数，单一指标无法全面反映某座电站与汇聚区的代表关系和一致性，为此，引入Spearman 相关系数和Kendall相关系数，结合多种数学相关系数从多个角度进行综合对比。因此本文中电站典型性与相关性类似，即为光伏电站与汇聚区的历史功率在较长时间范围内的一致性，相关系数越大，典型性越强。

2.1 3种数学相关系数

2.1.1 Pearson相关系数

Pearson相关系数是考察2个事物（经常为变量）之间的相关程度，定义为：

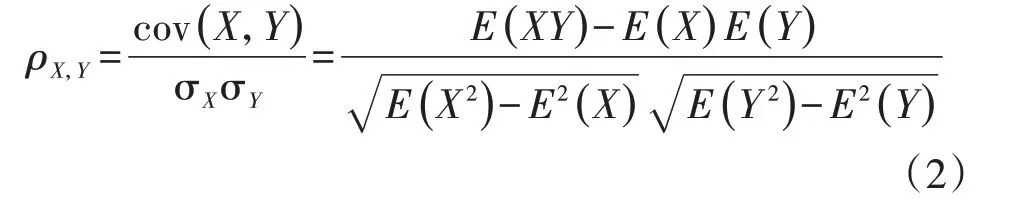
式中：ρX，Y为Pearson 相关系数；X、Y分别为不同的变量集合；cov（X，Y）为X和Y的协方差；σX和σY分别为X和Y的标准差；E（·）为数学期望。

2.1.2 Spearman相关系数

将变量集合X=｛x1，x2，…，xn｝（n为数据的数量）中元素按降序或升序重新排列得到A=｛a1，a2，…，an｝。将集合X中每个元素xi在序列A中的次序记为rg(xi)。同理按上述方法得到集合Y=｛y1，y2，…，yn｝中元素次序为rg(yi)。Spearman相关系数定义为：

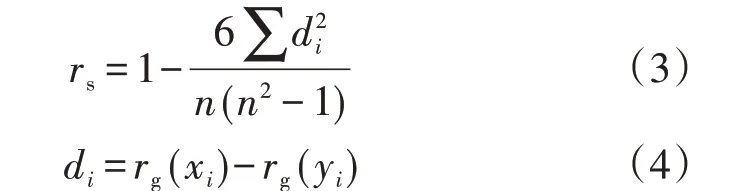
式中：rs为Spearman 相关系数；di为2 个次序rg(xi)与rg(yi)的差值。

2.1.3 Kendall相关系数

当集合X和Y中变量对(xi，yi)、(xj，yj)同时增减时，认为这2个变量一致；当其增减相反时，认为这2个变量不一致；当二者相等时，认为这2 个变量既不是一致也不是不一致。

Kendall相关系数定义为：

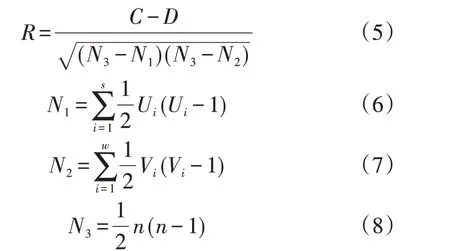
式中：R为Kendall 相关系数；C、D分别为有一致性、有不一致性的变量对数；s为变量集合X中由相同变量组成的子集合数，Ui为其第i个子集合所包含的变量数；w为变量集合Y中由相同变量所组成的子集合数，Vi为其第i个子集合所包含的变量数。

参考文献［15］将汇聚区中各电站的3 种相关系数结果按1∶1∶1 的权值进行组合计算，将相关关系表现最好、相关系数最大的电站作为该汇聚区中的典型代表电站。

2.2 典型代表电站相关性分析

为进一步证实通过3 种相关系数选择出的典型代表电站与汇聚区出力的一致性，选择以下4 类评价指标对汇聚区中的各电站分别进行分析。

1）季节性。根据历史出力数据，对比不同季节的典型日出力曲线，观察出力曲线呈现的特性。

2）气象典型日。根据已有的气象信息分别找出不同季节典型日（晴天、阴天）的出力曲线，观察不同曲线呈现的特点。

3）装机利用小时数。装机利用小时数可理解为电站在日内的使用时间，如式（9）所示。

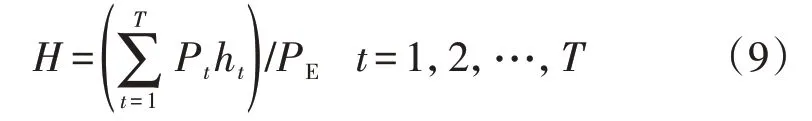
式中：H为装机利用小时数；T为时间段总数；Pt、ht分别为第t个时间段的功率和时长；PE为装机容量。

4）日内峰谷差及日内峰谷差占装机比重。峰谷差为日内功率最大值与最小值之差，即：

式中：Pdf为日内峰谷差；Ppeak为日内功率最大值，即顶峰功率；Pvalley为日内功率最小值，即低谷功率。

3 汇聚区出力预测模型

3.1 多输出SVM预测模型

SVM 是基于结构风险最小化理论和万普尼克-泽范兰杰斯维VC（Vapnik-Chervonenkis dimension）理论的一种小样本学习理论，使用领域较为广泛［16］。传统的SVM 无法满足预测多个变量的要求，借鉴滚动预测思想可实现多步骤滚动预测，虽然滚动预测原理简单，易于操作，但随着预测次数的增多，误差会迅速积累，导致最终结果失真，无法保持预测结果的准确性，因此舍弃该方法。结合SVM 本身输入、输出结构，参考文献［17］对其进行简化，在不改变训练数据输入值的基础上，依次对输出值对应的各个特征点进行预测，该方法可在保持SVM 优点的情况下不从底层对SVM 进行修改，其构造图如附录A 图A1所示。

3.2 区域功率预测模型

本文基于外推法和统计升尺度法［10，18］，结合多种数学相关系数，优化典型代表电站及原网络结构，建立24 h内的短期预测模型，模型建立步骤如下。

1）利用汇聚区中各电站的历史出力数据，结合3种相关系数计算得到典型代表电站。

2）将汇聚区中各电站的历史出力数据进行叠加形成基础资料，结合典型代表电站的历史出力数据及SVM 形成区域功率预测模型。模型输入为典型代表电站的历史出力数据，输出为对应日汇聚区历史出力数据。

3）在模型建立、训练之后，输入预测日典型代表电站预测值即可得到汇聚区功率预测值。

区域功率预测示意图如图2所示。

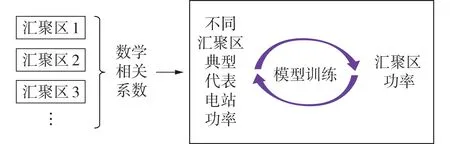
图2 区域功率预测示意图Fig.2 Schematic diagram of regional power forecasting

该方法主要利用历史出力数据进行数据处理，建模无需气象数据，且避免了常规叠加法导致的误差累积问题，已有研究［19］证实了本文思路的正确性。由于光伏曲线的固有特性，因此更易找到单站功率与汇聚区功率间的非线性联系，从而建立较准确的预测模型，同时减少预测误差。为验证本文方法的有效性，后文利用单机等值法［20］和叠加法进行对比。

3.3 区域功率预测流程

基于上述原理，本文通过以下步骤得到区域光伏功率短期预测结果。

1）划分汇聚区。基于K-means 聚类方法的工作原理和计算方法，利用历史出力数据、气象数据和特性数据进行聚类划分，并判断汇聚区是否只有一座电站，如果是，则直接转至步骤3），组成单站预测模型并输出结果，否则，继续执行步骤2）。

2）选择典型代表电站和指标评价。基于外推法和统计升尺度法，计算各汇聚区中各电站3 种相关系数，选择对应汇聚区典型代表电站；用4 类出力指标对汇聚区中各电站在多个时间节点进行相关性分析，验证典型代表电站的最优性及代表性。

3）建立区域功率短期预测模型。将计算得到的典型代表电站与汇聚区历史数据构成区域功率预测模型（具体见3.2节）。

预测流程图如附录A图A2所示。

4 算例分析

4.1 算例简述

本文所采用的算例为云南省大理州与楚雄州2017 年5 月至9 月有记录的光伏电站，电站具体名称如附录A表A1所示。

4.2 汇聚区划分

利用已有的数据资料，采用K-means聚类方法进行循环计算，表1为大理州类别数与距离和的关系。

由表1 可知，类别数为4 时距离和下降速度最快，故选择划分类别为4 类，具体划分结果为：汇聚区Ⅰ，电站1-1、1-3、1-6；汇聚区Ⅱ，电站1-2、1-5、1-7、1-8；汇聚区Ⅲ，电站4；汇聚区Ⅳ，电站1-9。

表1 大理州类别数与距离和的关系Table 1 Relationship between category number and distance sum of Dali prefecture

根据计算结果，对汇聚区I中的3 座电站和汇聚区Ⅱ中的4 座电站进行区域短期功率预测。同理，对楚雄州的汇聚区进行类似划分，划分结果为：汇聚区Ⅴ，电站2-1、2-5、2-6、2-9；汇聚区Ⅵ，电站2-2、2-3、2-4、2-7、2-8。

4.3 典型代表电站选择及相关性分析

利用3 种相关系数选择典型代表电站并利用4类指标进行相关性分析，以大理州汇聚区Ⅰ为例。

表2为大理州“大佛山+干塘子+西村”汇聚区Ⅰ典型代表电站选取情况。

表2 汇聚区I各电站相关系数Table 2 Correlation coefficient of each station in Convergence Area Ⅰ

由表2 可知，西村展示出较强的代表性及与汇聚区的相关关系，其3 种单一相关系数均高于汇聚区中的其余电站。为进一步说明典型代表电站选取的正确性，利用各指标对电站进行评价，如图3—6所示，同时利用各指标分别计算汇聚区中各电站与汇聚区的相关系数，结果如表3 所示。由于自身出力的特殊性，光伏电站在夜晚以及清晨等时间出力几乎为0，综合考虑后取96点出力数据（以15 min为间隔）中08:00—18:00共41点的出力序列。

图3 单站与汇聚区季节性对比Fig.3 Seasonal comparison between single station and convergence area

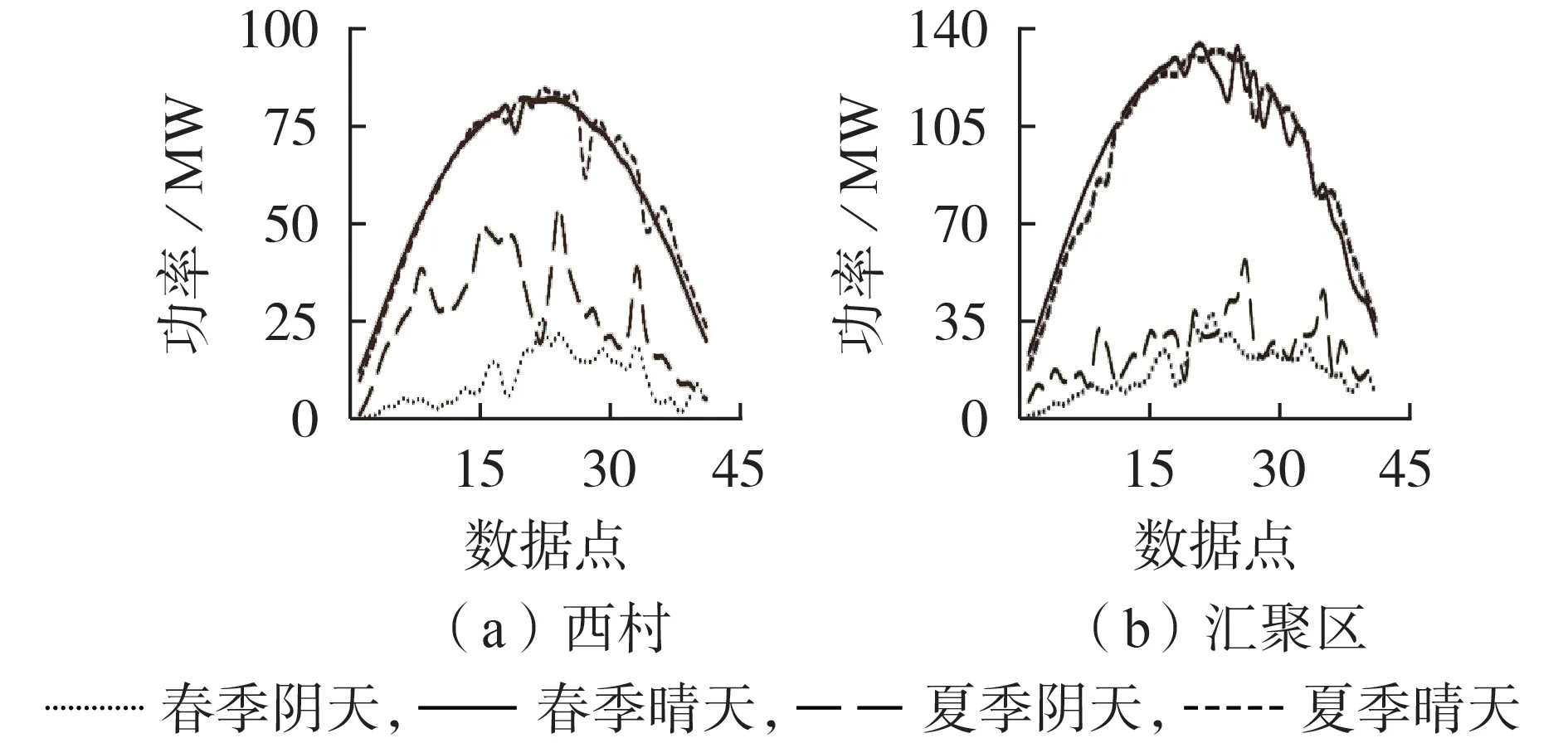
图4 单站与汇聚区气象典型日对比Fig.4 Typical meteorological day comparison between single station and convergence area

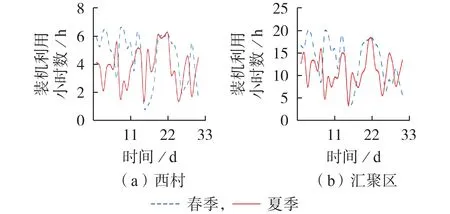
图5 单站与汇聚区装机利用小时数对比Fig.5 Installed utilization hour comparison between single station and convergence area

图6 单站与汇聚区日内峰谷差对比Fig.6 Intraday peak valley difference comparison between single station and convergence area

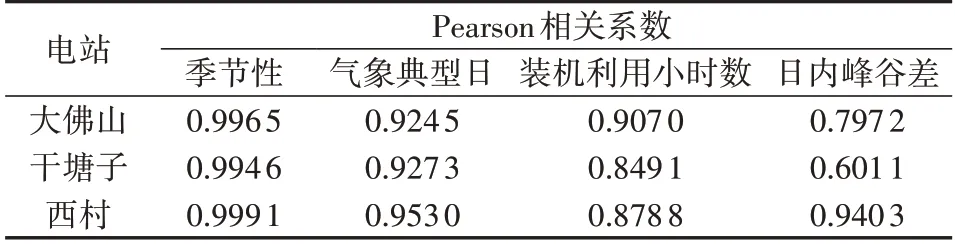
表3 相关性综合对比Table 3 Comprehensive comparison of correlation

最终发现西村的3 种指标均优于其他电站，证明利用3 种相关系数选择汇聚区中典型代表电站的方法较为准确。

4.4 短期出力预测结果

采用本文方法分别计算各电站预测精度，同时将本文方法和其他方法进行对比，计算结果分别如表4、表5 和图7 所示。可知本文方法的预测精度优于叠加法和单机等值法。

图7 汇聚区Ⅰ光伏功率预测值与实际值对比Fig.7 Photovoltaic power comparison between forecasting and actual values in Convergence Area Ⅰ

表4 汇聚区Ⅰ各电站预测精度Table 4 Forecasting accuracy of each power station in Convergence Area Ⅰ单位：MW

表5 汇聚区Ⅰ预测精度对比Table 5 Forecasting accuracy comparison of Convergence Area Ⅰ单位：MW

大理州和楚雄州部分汇聚区3 种方法的结果对比如附录A 表A2—A4 所示。由表A2、表A3 可知：相关系数较大的典型代表电站在相关性分析的表现上也优于汇聚区中的其他电站，这说明典型代表电站与汇聚区在历史功率方面的高度一致性；本文方法的RMSE、MAE 均优于其他2 种方法，其中多个汇聚区的RMSE小于10 MW；虽然典型代表电站的单站预测误差较小，均在10 MW以下，但将预测数据叠加后却没有展现出较好的预测效果，因此虽然叠加法的计算过程较简单，但在精度要求较高时推荐使用其他方法。由表A4知：除10月7日的汇聚区Ⅰ外，各汇聚区在不同日期采用本文方法得到的误差最小；10月7日所有汇聚区采用3 种方法得到的预测误差均较大，这是由于假期或突发事件导致预测值误差增大，但综合而言本文方法较准确；单机等值法的预测精度也较高，但是该方法在建模过程中需要的资料远多于本文方法，这将会在整体预测流程中消耗过多时间，此外，单机等值法精度提升较困难，而本文方法由于预测模型的特点，可通过典型代表电站单站预测技术的提高进一步提升区域功率预测的精度。