基于机器学习的气固流化床最小流化速度预测

包国强，顾维根，穆维国，周 南，崔 森，李志强,，李妍娇，周恩会，，4，赵跃民，，4，董 良，，4

(1.国家能源集团 新疆能源有限责任公司，新疆 乌鲁木齐 830002；2.中国矿业大学 人工智能研究院，江苏 徐州 221116；3.中国矿业大学 化工学院， 江苏 徐州 221116；4.煤炭加工与高效洁净利用教育部重点实验室(中国矿业大学)，江苏 徐州 221116)

0 引 言

气固流化床由于其传热、传质效率高，床层稳定性好等特点，已被广泛应用于煤化工、煤燃烧和煤炭分选等工业领域[1-3]。其中最小流化速度是流化床运行最重要参数之一。作为固定床向流化床变化的转折点，最小流化速度是流态化领域研究的热点。其中ERGUN和ORNING[4]提出的床层压降方程用于预测最小流化速度应用较为普遍。

由于机器学习[5-6]预测精度较高，在学术界和工业界影响逐渐增大，并在化工领域也得到了广泛的应用。机器学习可大幅降低模型复杂性，提高预测精度，并得到更为完善且更适用的模型[7]。在机器学习中，决策树是一种决策支持工具，是利用树状图形或模型来辅助决策[8]。随机森林是一种相对较新的数据挖掘方法，是在分类和决策树的基础上发展起来，用于处理变量之间的非线性关系[9]。随机森林算法实现简单、精度高、抗过拟合能力强，当面对非线性数据时，适于作为基准模型[10]。

针对最小流化速度，由于实际过程中很难获得颗粒的球形度以及床层的最小空隙率，因此，各国学者对ERGUN的方法进行了简化处理，建立了许多经典模型[11-22]。经典模型虽能在一定程度上对最小流化速度进行预测，但模型通常是根据几个影响因素的几个试验点开发，模型预测精度存在较大误差。因此，有必要通过机器学习和数据挖掘方法，从颗粒性质(密度、粒度)与设备条件等方面综合考虑，研究气固流化床的最小流化速度，以系统评估对最小流化速度的综合影响。笔者采用随机森林验证了其预测最小流化速度的可行性，并考察了设备参数、颗粒密度和颗粒粒度共3个影响因素在预测最小流化速度时的相对重要性。随机森林模型的准确预测和模型背后的新见解为最小流化速度提供了全面的理解，并为流态化理论计算以及工业放大提供了指导。

1 研究方法

1.1 数据的收集

诸多学者在理论分析和试验测定的基础上，建立了许多经验或半经验的关联式计算最小流态化速度，见表1。

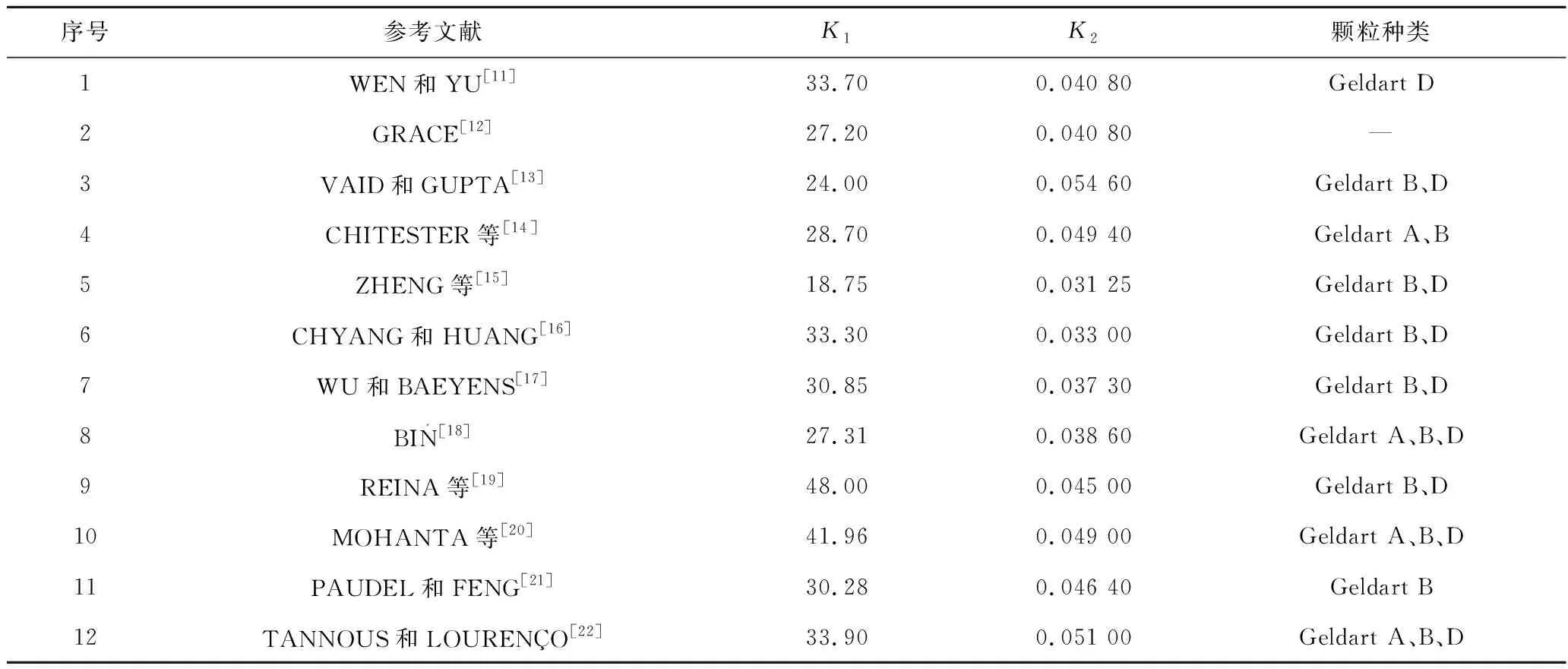
表1 气固流化床中最小流化速度模型

K1、K2为学者基于最小流化速度公式Remf=

(K2+K2Ar)1/2-K1(其中，Remf和Ar分别为最小流化气速条件下的雷诺数和阿基米德数，根据颗粒形状和颗粒间堆积空隙率对其修正所得到的参数)。但由于研究所采用的物料不同，得到的关联式在预测的准确性和适用性方面也不尽相同。通过整理相关文献，考察了颗粒性质(密度、粒度)与设备条件(床体直径)对最小流化速度的影响。最小流化速度的试验数据见表2。由表2可得到26个输入变量、最小流化速度的上下限，并通过箱线图得到了特征数据的统计分布。任何2个变量之间的线性相关性由皮尔逊相关系数衡量。

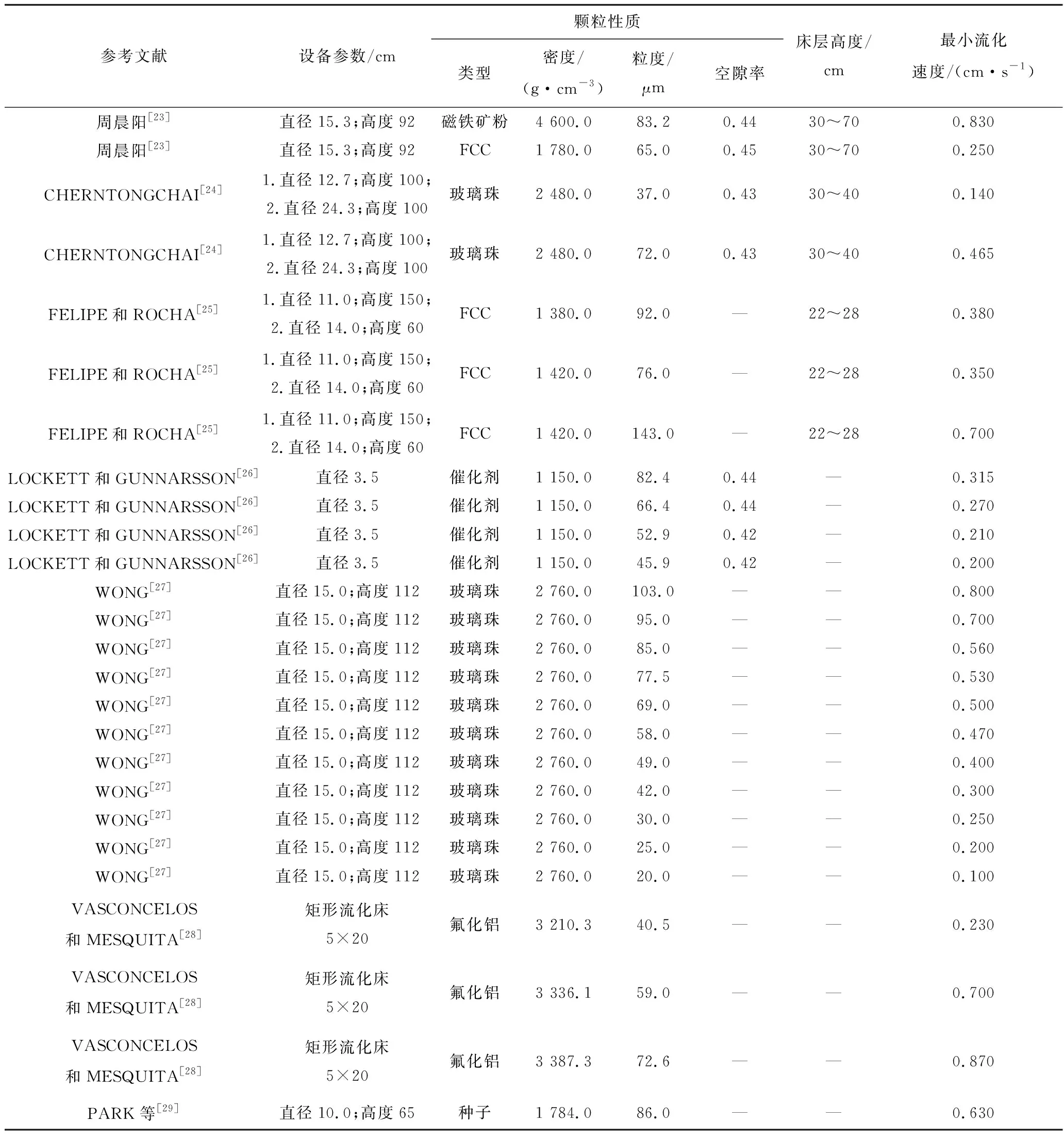
表2 Geldart A类颗粒最小流化速度的试验结果

皮尔逊相关系数r定义为

(1)

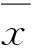
1.2 随机森林回归和验证

数据规范化(归一化)处理是数据挖掘的一项基础工作。不同评价指标往往具有不同的量纲，数值间的差别可能很大，不处理可能会影响数据分析结果。为了消除指标之间的量纲和取值范围差异的影响，需要进行标准化处理，将数据按照比例缩放，使之落入一个特定的区域，便于进行综合分析。作为输入的影响因素的数据首先通过公式(2)进行数据归一化处理：

(2)

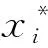
应用随机森林对气固流化床的预测模型进行训练和优化。随机森林的实施分为以下3个子步骤[7]：① 随机采样，将数据集替换为多个子样本；② 用不同的子样本训练决策树，其中每棵树根据训练数据的自举复制尽可能地生长，每个叶子节点输出节点中所有标签值的平均值；③ 最后通过对所有树的性能进行平均，获得最终估计值。将全部数据随机分为训练组和测试组，比例为70∶30。随机森林模型的5个调谐参数包括决策树的数量、寻找最佳分割时要考虑的特征数量、树的最大深度、分割内部节点所需的最小样本数量以及位于叶节点所需的最小样本数量。决定系数也称为拟合优度，用于评价拟合的好坏，决定系数越高，代表可以被解释的程度越高，回归模型的效果越好。使用决定系数[30-31]可在测试集上评估模型的性能。

决定系数定义为

(3)

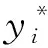
超参数是用训练组的数据通过网格搜索算法确定的。对决策树的数量应用循环语句，通过10倍交叉验证找到最佳超参数，衡量指标是决定系数，然后使用最佳参数重新训练模型，并用剩余的30%数据进行测试。通过网格搜索算法，分割最小数量、树的最大深度、节点内最小样本数量、最小子叶节点数分别为2、10、2、1。决策树的数量取每10个数作为一个阶段，来观察决定系数的变化，通过运行网格搜索算法，结果如图1所示，当决策树的数量达到151时，决定系数最高。

图1 决定系数与决策树数量关系Fig.1 Relation diagram between decisioncoefficient and decision tree quantity

部分相关图和相对重要性分数用于解释影响变量的重要性。FRIEDMAN[32]为了理解预测对每个影响变量的依赖性质，引入了部分依赖图。通过选择影响变量的多个值，使用其他影响变量的所有情况下的每个值预测输出，然后计算所有情况下的平均输出，可以获得部分相关图。单个随机森林中影响变量的相对重要性分数可以通过由该影响变量确定的所有分割平方改进总和来获得[33]。

2 结果和讨论

2.1 特征变量统计结果和任意2个变量线性关系

根据收集的数据集，获得了特征数据的箱线图统计分布，如图2所示。设备条件(床体直径)、颗粒性质(密度、粒度)以及最小流化速度的数值分布变化范围和离散幅度较大，且不同特征变量的数量级相差较大。其中，床体直径变化在3.5～20.0 cm；颗粒密度变化在1 150～4 600 g/cm3；颗粒粒度变化在20～143 μm；最小流化速度变化在0.10～0.87 cm/s。综上可知，各变量数据值极差较高，对预测模型的鲁棒性具有一定的挑战。为了进一步分析收集的数据集各个特征变量间的相互关系，对各个变量进行了皮尔逊相关系数分析，相关系数R的绝对值越大，特征之间的相关性越大。收集特征变量间相关性矩阵热图如图3所示。由图3可知，最小流化速度与颗粒粒径、颗粒密度和床体直径均呈正相关，相关系数分别为0.79、0.31、0.14。颗粒粒径对其影响最大，颗粒粒径增大，最小流化速度也随之增大。应用机器学习方法建立了一个高质量的预测模型，并探讨了各影响因素的相对重要性以及输入变量之间的相互作用。

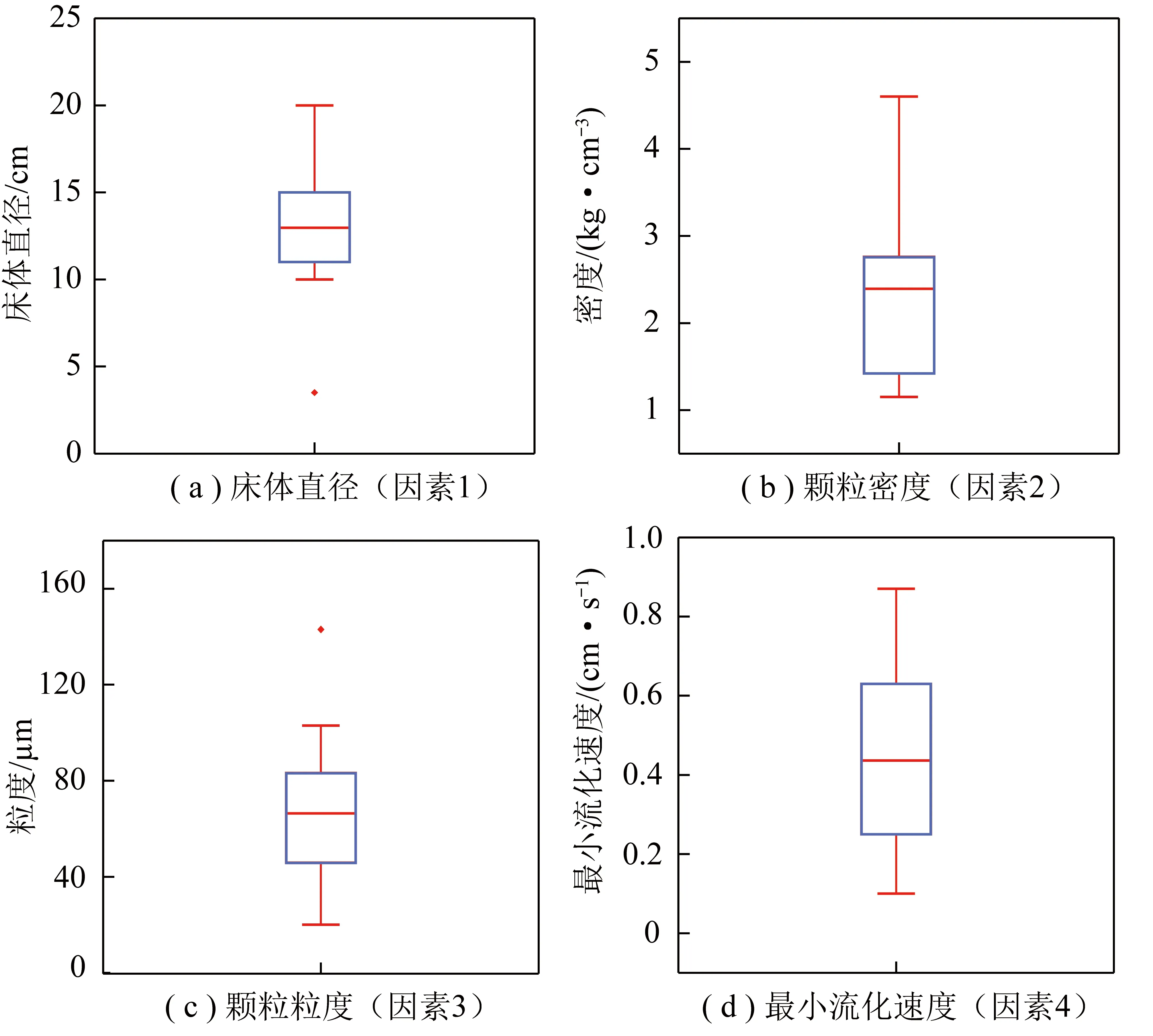
图2 收集特征变量的箱线图Fig.2 Box plot for collecting characteristic variables

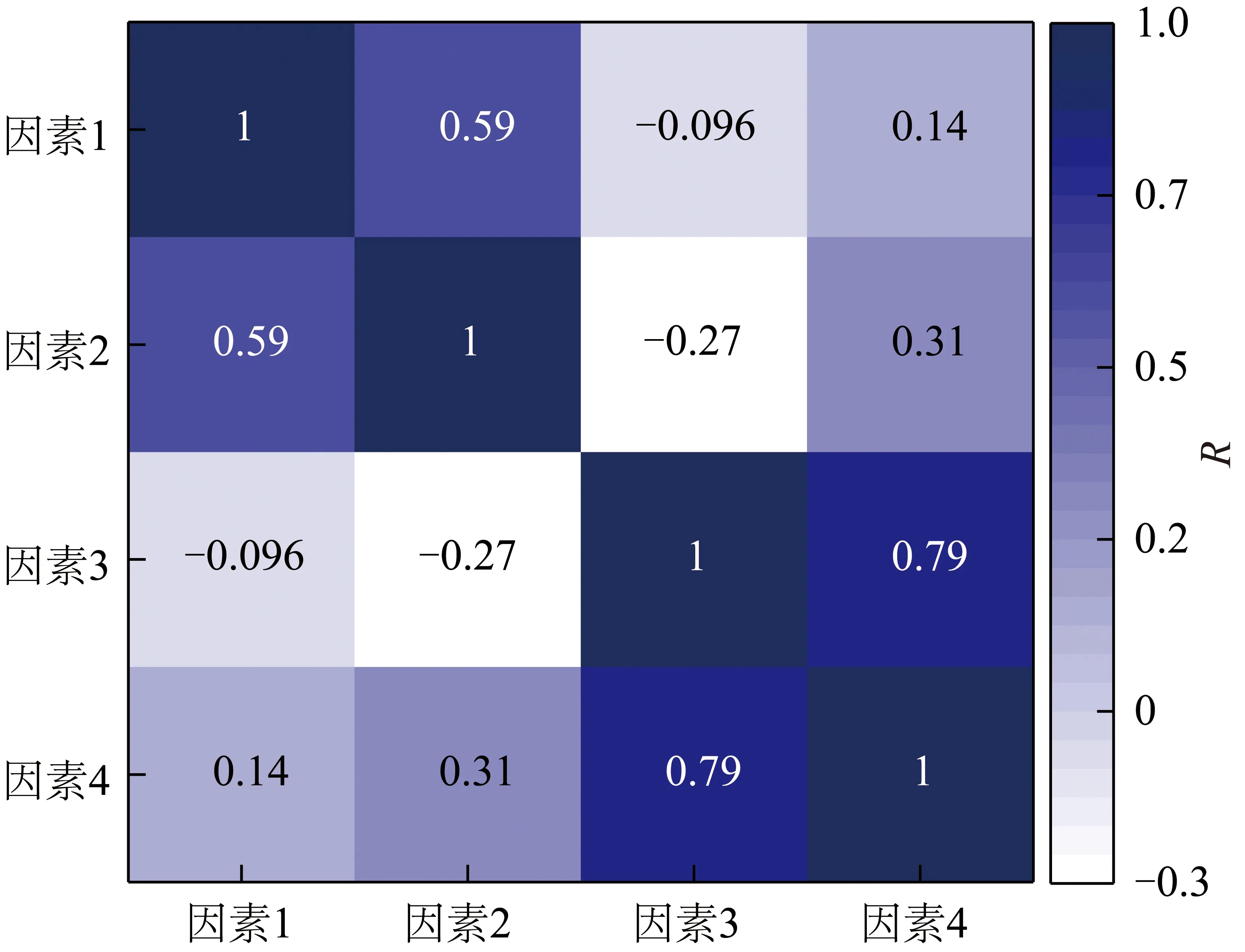
图3 收集特征变量间相关性矩阵热图Fig.3 Collect the heat map of correlation matrixbetween characteristic variables

2.2 最小流化速度的随机森林模型性能评估

随机森林算法的超参数与最佳模型相对应，通过10倍交叉验证，分别用于对不同输入变量的最小流化速度预测模型的再训练。开发模型的性能如图4所示。图4(a)显示了最佳随机森林模型在测试集上预测的最小流化速度预测值与试验值的对比结果，图4(b)显示了最佳随机森林模型在测试上获得了最大决定系数0.875，实现了较低的损失和较高的决定系数。因此，最佳随机森林模型可以很好地推广到测试集上，最佳随机森林模型在预测最小流化速度方面较为准确。

图4 测试集上最佳随机森林模型的性能Fig.4 Performance of the optimal random forest model on the test set

2.3 最小流化速度预测部分相关图

床层直径、颗粒密度和颗粒粒度的数值作为因素特征用于最小流化速度预测，评估了各因素对最小流化速度的相对重要性。如图5所示，所有重要性分数的总和被定标为1，各特征因素的重要性由大到小依次为：颗粒粒径、颗粒密度和床体直径。该排序与文中各个变量的皮尔逊相关系数分析的相关性结果一致。颗粒粒径的重要性得分为0.783，成为最小流化速度最敏感的变量，超过了颗粒密度的权重，远超过了床体直径的权重。床体直径的重要性得分为0.018 78，对最小流化速度的影响较小。颗粒粒度对最小流化速度的影响最大，而床体直径影响最小，该结论与付芝杰[34]的研究结论相符。

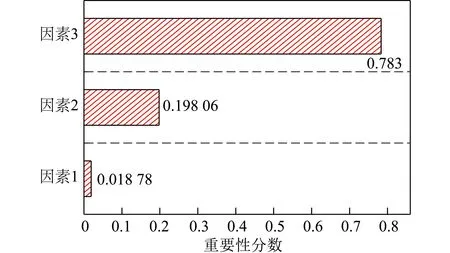
图5 影响变量的重要性得分Fig.5 Importance score of the influencing variables

在确定了每个输入特征变量的相对重要性之后，需要更好地理解输入变量和输出变量之间的依赖关系。一般来说，当一个影响变量发生变化时，输出响应越大，该影响变量就越显著。此外，通过分析输出随该影响变量的变化，可以观察到影响变量和输出变量之间呈正相关或负相关。通过对所有特征的值进行平均，部分相关图被用于可视化某1个或2个特征对最小流化速度的总体影响趋势。单向部分依赖性的结果如图6所示，其中x轴上的刻度表示目标特征值的分形，反映了数密度。由图6可知，颗粒粒度对最小流化速度的影响呈近似线性上升，但斜率随着粒径的升高而逐渐减小，如图6(a)所示。颗粒密度对最小流化速度的整体影响线性上升波动较低，颗粒密度在1 150～4 600 g/cm3时，斜率随着密度的升高而几乎保持不变，如图6(b)所示。床体直径对最小流化速度的影响最小，其依赖性为近似水平的直线，如图6(c)所示。部分相关图和影响变量的相对重要性分数揭示了重要的发现，并指出最小流化速度预测的研究潜力。

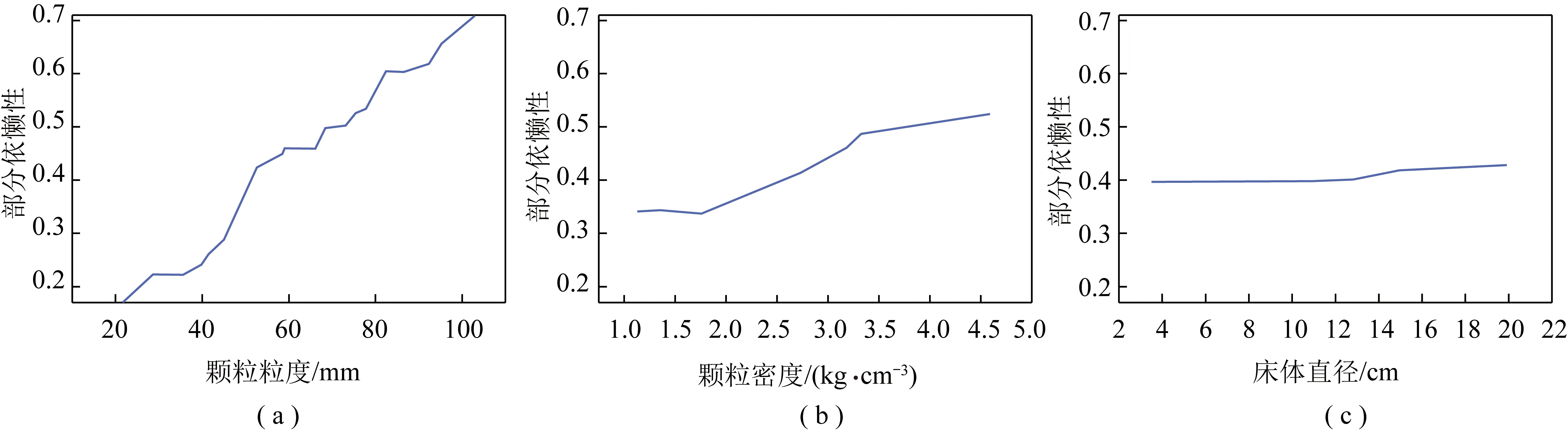
图6 预测最小流化速度的最佳随机森林模型中特征变量的部分相关图Fig.6 Partial correlation diagram of characteristic variables in an optimal random forest model for predicting the minimum fluidization rate

3 结 论

1)利用随机森林的机器学习方法，从床层直径、颗粒密度和颗粒粒度3个方面预测了气固流化床的最小流化速度。最小流化速度与颗粒粒径、颗粒密度和床体直径均呈正相关，皮尔逊相关系数分别为0.79、0.31、0.14，颗粒粒径与最小流化速度相关性最强。

2)通过网格搜索算法，得到了最佳随机森林模型，并在测试上获得了最大决定系数0.875，实现了较低的损失和较高的决定系数。

3)通过部分相关图和影响变量的相对重要性分数分析，得知颗粒粒径对气固流化床的最小流化速度的变化起主要作用。同时，得到了各特征因素对最小流化速度的影响方式，同时验证了收集特征变量间的皮尔逊相关系数分析的正确性。