考虑信号配时引起延误的改进Frank-Wolfe算法

苗泽霖，刘 邓，任雪晴，赵浩淋

(北方工业大学城市智能交通控制技术重点实验室，北京 100144)

0 引言

驾驶者的路径选择行为导致的最主要的结果就是路网中交通流量的重新分配，交通分配是指交通需求基于已知的道路网络参数信息，在路网上进行规则分配，其中涉及驾驶者的路径选择行为和如何均衡的分配等问题.最初研究学者大多使用全有全无(All-or-Nothing)的方法分配流量，该方法的使用场景为：简单的城市路网，车辆不会出现排队等待，并且路段的时间成本不随交通量的改变而改变.20世纪50年代，Wardrop[1]提出了网络平衡分配的第1、第2原理，随后该原理在交通流量分配中被广泛应用.在实际的交通出行中，人们更加青睐于通过第1种分配原理来进行交通流量分配.随后，Beckmann等[2]用数学语言描述了这一问题，并提出相应的数学规划模型.LeBlanc等[3]使用Frank-Wolfe算法对规划模型进行求解.LeBlanc[4]通过实例验证了该算法用于交通流量分配的可靠性，从而形成了现在的实用解法.在此之后，交通工作者们又分别通过改进Frank-Wolfe算法的搜索步长和搜索方向给出了各种不同的改进Frank-Wolfe算法[5-7]，提升算法的运行效率.然而，在现实中，路网交通量的分配受到信号控制的影响，Frank-Wolfe算法无法用于求解信号控制网络中的路段交通量.在信号控制网络中计算最短路径时，许多工作都涉及转向延迟和停车延误问题.Ziliaskopoulos等[8]在1966年提出了一种有效的方法，对交叉口的交通流移动进行惩罚来解释这些延迟.Chen and Yang[9]提出了一种计算周期性交通信号控制下的交叉口惩罚的方法，并给出了计算这样一个网络的最小时间路径.

在现实中，路网交通量的分配受到信号控制的影响，Frank-Wolfe算法无法用于求解信号控制网络中的路段交通量.基于此，本文考虑路网中交叉口信号控制的影响，在计算各个路段的阻抗函数时，把信号控制所引起的延误作为自变量加入到其中，通过更新阻抗函数，确定OD对之间的最短路径进而求解出各路段相应的路段交通量.

1 Frank-Wolfe算法

1.1 用户平衡分配模型

1.1.1 模型中所用的变量和参数

表1 模型中所用的变量和参数

1.1.2 交通平衡分配模型

Beckmann提出的具有固定需求的用户均衡模型(User Equilibrium，UE)如下：

(1)

(2)

(3)

(4)

本文在前者的基础上把信号控制所引起的延误作为自变量加入到路段阻抗函数ta(xa)中，得到新的阻抗函数ta=ta(xa,ψa)，其中ψa为路段a对应的下游交叉口信号控制所引起的延误. 使用新的阻抗函数进行交通量分配，不仅可满足用户均衡原理，还可充分考虑信号配时参数对分配结果的影响.

1.2 Frank-Wolfe算法简介

Frank-Wolfe算法是一种基于迭代下降的优化方法.该算法主要根据一组线性规划的最优解确定下一步的迭代方向，然后根据目标函数的一维极值问题求最优迭代步长，其中路段阻抗函数最为关键.阻抗函数是以路段流量为自变量的函数，也称为行程时间函数，与交通量密切相关.在实际情况中，路段阻抗除了受路段流量的影响之外，还受交叉口信号控制的影响，驾驶员在进行路径选择时，往往会考虑到交叉口信号控制的影响.因此，为了使流量分配更符合实际需要，在改进的算法中，将由信号控制所引起的延误以惩罚值的形式加入到阻抗函数中.

2 改进Frank-Wolfe算法

2.1 在阻抗函数中加入惩罚值

2.1.1 惩罚值的计算

在受信号控制的交叉口中，连续的车流由于受到信号相位的控制，因而会被暂时分开避免出现冲突.特定的交通流只能在特定信号相位内被允许通行，如果在当前的信号相位内，车辆到达交叉口时不被允许通行，驾驶者只能等到允许通行的相位开始后才可通行.从车辆到达交叉口的那一刻到允许通行信号相位开始的这段时间，交通流想要通行的意图是被允许的，我们将这段时间称为这股交通流的惩罚值.本文为了计算简便，假设车辆在交叉口的等待时间不会超过1个信号周期，即路口处没有出现排队状况.对于一股给定的交通流，惩罚值的大小取决于车辆到达交叉口的时间，我们把研究期间内每个时刻的惩罚值构成一个惩罚向量，随着信号周期的重复，惩罚值也会不断重复，因此惩罚值也是和周期时长密切相关的.下面通过1个例子来说明如何将延误以惩罚值的形式加入到路段阻抗函数中.

车辆从交叉口A行驶到交叉口B，交叉口B为十字路口，共包含2个信号相位，相位a和相位b的持续时间分别为20 s和18 s，信号相位按照a→b→a→b的顺序交替进行循环.路段AB阻抗值由2部分组成，路段AB的行驶时间和交叉口B信号控制延误的惩罚值，不同的行驶时间对应的惩罚值不同(见图1).

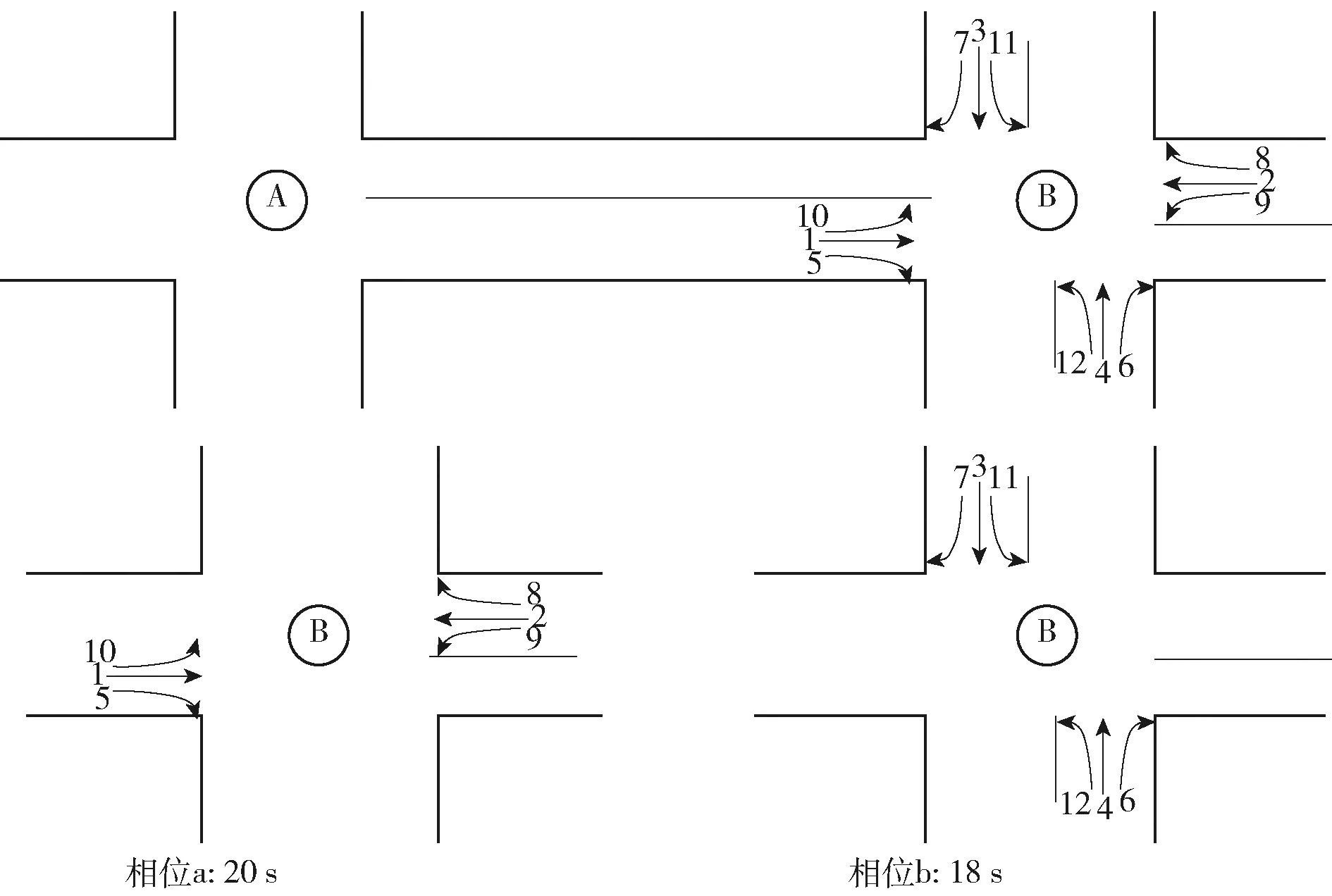
图1 交叉口相位分布和各个相位绿灯持续时间

假设相位a在t=1 s开始显示绿灯，车辆在路段AB上的行驶时间为27 s，即在t=27有车辆由西向东驶入交叉口B，并计划继续向东行进，该车辆只允许在相位a为绿灯时通行.在t=27 s时相位b为绿灯，相位a为红灯.因此该车辆在t=27 s时需要等待，从开始等待到下一个周期相位a开始显示绿灯(t=39 s)的这段时间，称为相位a在t=39 s的惩罚值，即ψa(27)=12.所以车辆在路段AB上的阻抗值tAB=27+12=39 s.表2显示交叉口B在不同时刻下不同相位所对应的惩罚值.如果车辆在路段AB上的行驶时间为18 s，即t=18 s时，相位a在t=18 s的惩罚值为ψa(18)=0，车辆在路段AB上的阻抗值tAB=18+0=18 s；如果车辆在路段AB上的行驶时间为29 s，即t=29 s时，相位a在t=29 s的惩罚值为ψa(29)=10，车辆在路段AB上的阻抗值tAB=29+10=39 s.由于不同的行驶时间对应的惩罚值不同，因此，在计算路段阻抗时，将由信号控制所引起的延误以惩罚值的形式加入其中.

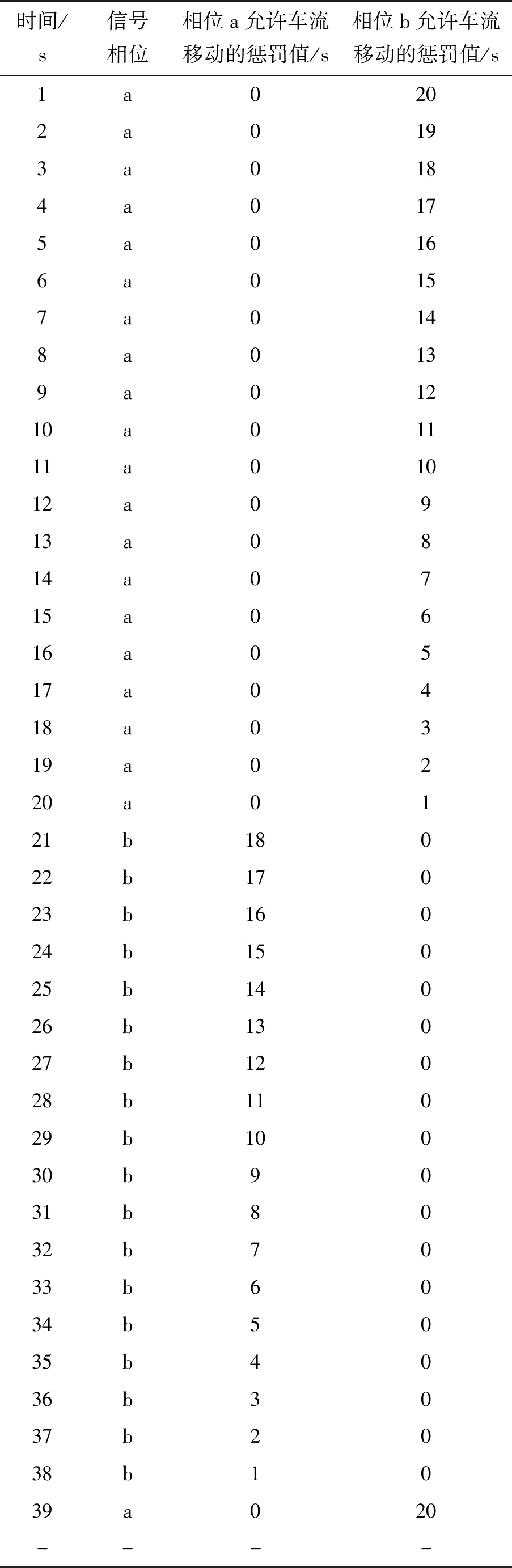
表2 所有交叉口车流所对应的信号相位和相应惩罚

2.1.2 在阻抗函数中加入惩罚值

车辆在进行路径选择的时候，除了考虑各路段行驶时间之外，还应该考虑在交叉口处由于信号控制而引起的等待时间.将信号控制所引起的延误转化为惩罚值，加入到阻抗函数中，具体做法如下：

步骤1根据交叉口的信号控制参数，计算得到各相位在不同时段的惩罚值列表TT.需要注意，在计算不同交叉口的惩罚值时应该考虑到相邻交叉口之间相位差的存在，相应的相位开始时间也应该向后延迟.

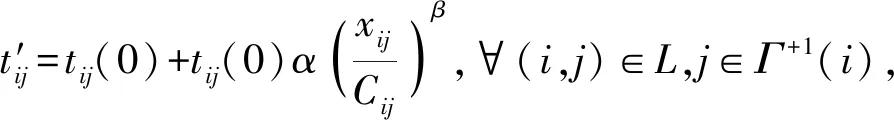
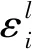
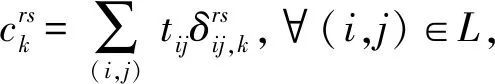
2.2 改进Frank-Wolfe算法

考虑交叉口信号控制引起延误的影响，改进后的算法主要在路段阻抗的计算过程，并将延误以惩罚值的形式加入其中，在进行迭代优化的过程中，使用新的阻抗函数选择最短路径. 交通路网中所有的信号控制参数都是提前知道的，各OD对之间的路径也是已知的. 在使用改进Frank-Wolfe算法分配交通流之前，先计算各交叉口的惩罚值列表TT.将信号控制所引起的延误转化为惩罚值，加入到阻抗函数的计算中，之后在进行路段流量分配. 步骤如下：

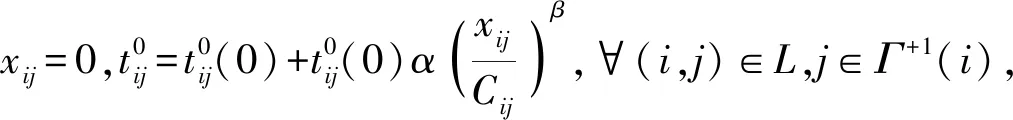
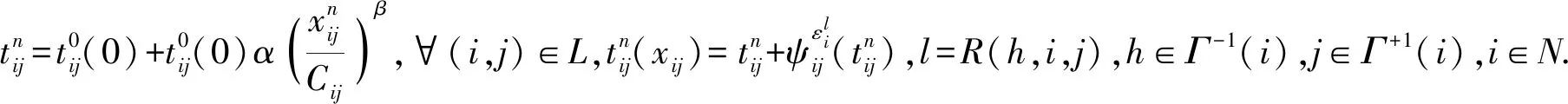
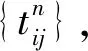
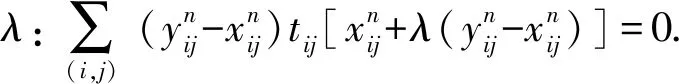
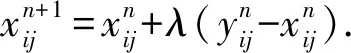
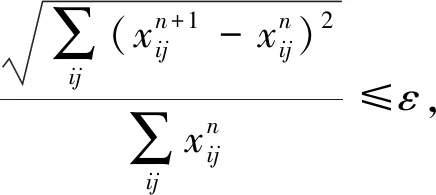
3 算法复杂度分析

计算时间复杂度，假设交通网络交叉口个数为n，OD对的个数为g，在求解交通流量分配时的迭代数为l，步骤3中求解最短路径，时间复杂度为O(n2)，原Frank-Wolfe算法的时间复杂度为O(gln2). 将惩罚值加入到计算阻抗函数的过程中之后，OD间的所有路径的最大个数仍然为n(n-1)，因此改进Frank-Wolfe算法的时间复杂度没有变化，仍然为O(gln2).

4 算例分析

4.1 仿真案例

为了验证改进算法的有效性，通过下列算例来进行分析和说明. 路口网络图见图2. 图3中各个路段的相关参数见表3. 路网共有4个起点(o1=1，o2=2，o3=3和o4=4)，2个终点(d1=5和d2=6)，4个OD对(1→6、2→5、3→6、4→5)，且OD矩阵Q为：

表3 交通路网的路段参数

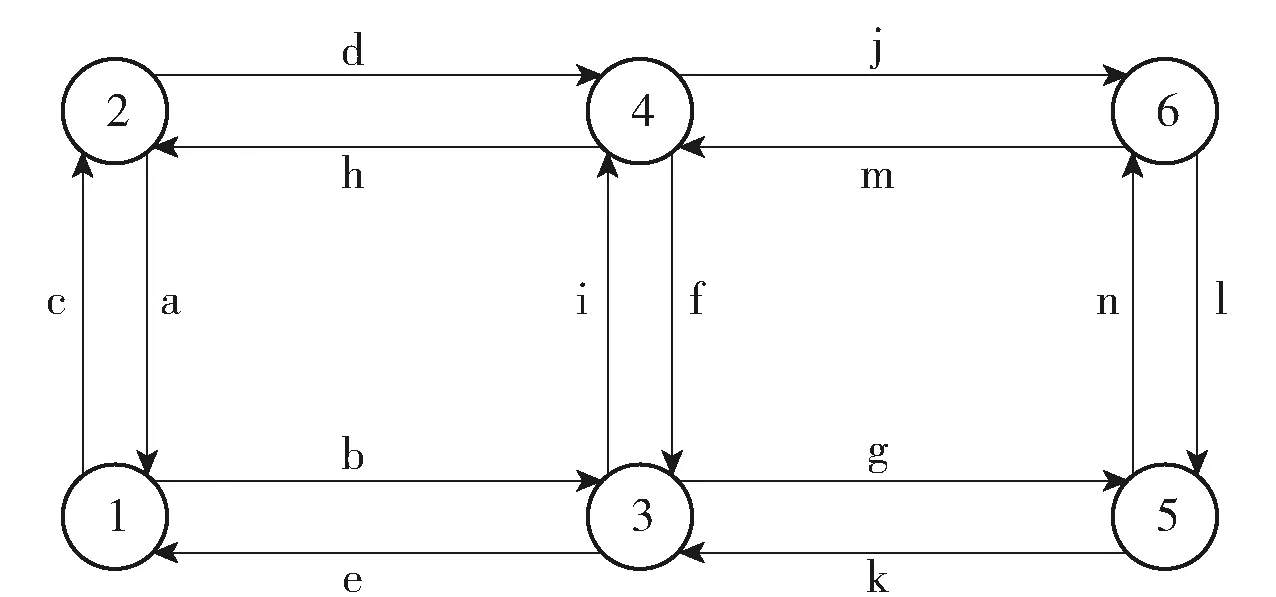
图2 网络简图

模拟1个受信号控制的交通网络，包含6个交叉口和14条道路，其中6个交叉口均受交通信号控制，车道和其相应的相位如图3所示. 各交叉口均为两相位交叉口，各个交叉口信号控制参数见表4. 为了便于计算，假设每条路段的通行能力相同，且Ca=950 veh/h；每个交叉口的总损失时间相同，Li=10 s.

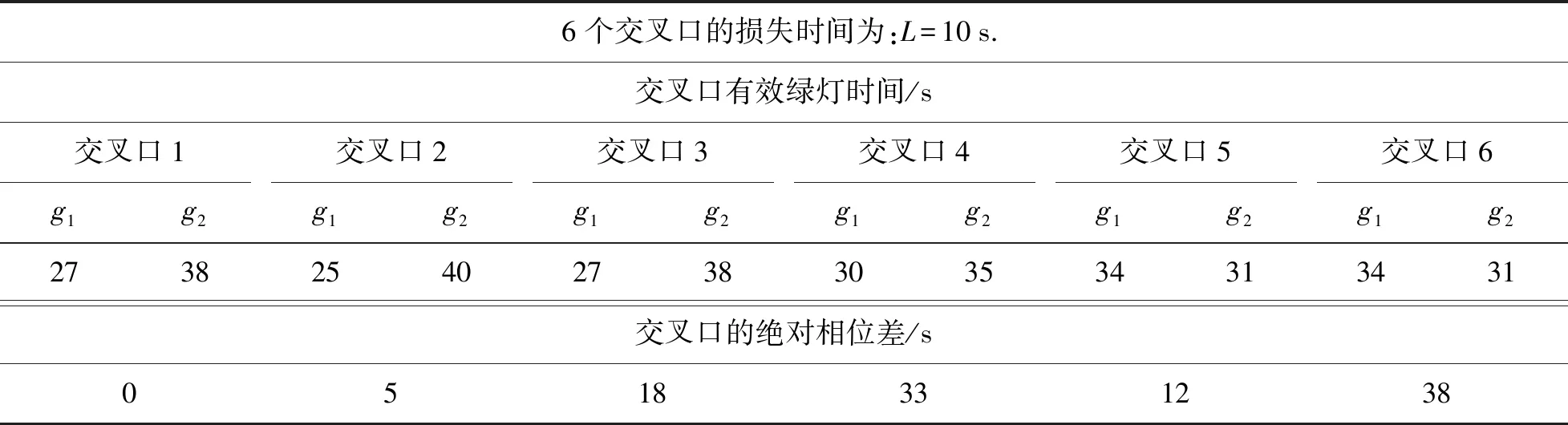
表4 交叉口信号控制参数

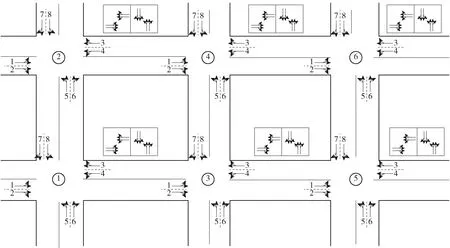
图3 算例网络

4.2 案例计算

根据交通路网信息和信号控制参数，先计算各交叉口各相位对应的惩罚值，由此得到惩罚值列表TT. 根据该列表，通过算法计算，可得到图2所示网络中各个OD对的最短路径集合. 对于OD对16来说，最短路径为：1→2→4→6，u16=75；对于OD对25来说，最短路径为：2→1→3→5，u25=99；对于OD对36来说，最短路径为：3→4→6，u36=53；对于OD对45来说，最短路径为：4→3→5，u45=90. 然后根据所求得的最短路径进行路段流量分配，算法运行共迭代15次，满足设置终止条件(ε=0.005)，所得各个路段交通量的最终结果见表5，流量数据保留到整数.

4.3 结果分析

通过MATLB编程，采用原Frank-Wolfe算法，即不考虑交叉口信号控制对流量分配的影响，在相同的路网结构和OD交通需求下求解上述算例，结果如表5所示，Δxa表示相同路网结构和OD交通需求下改进后的Frank-Wolfe算法和原Frank-Wolfe算法所得路段交通量的差值.

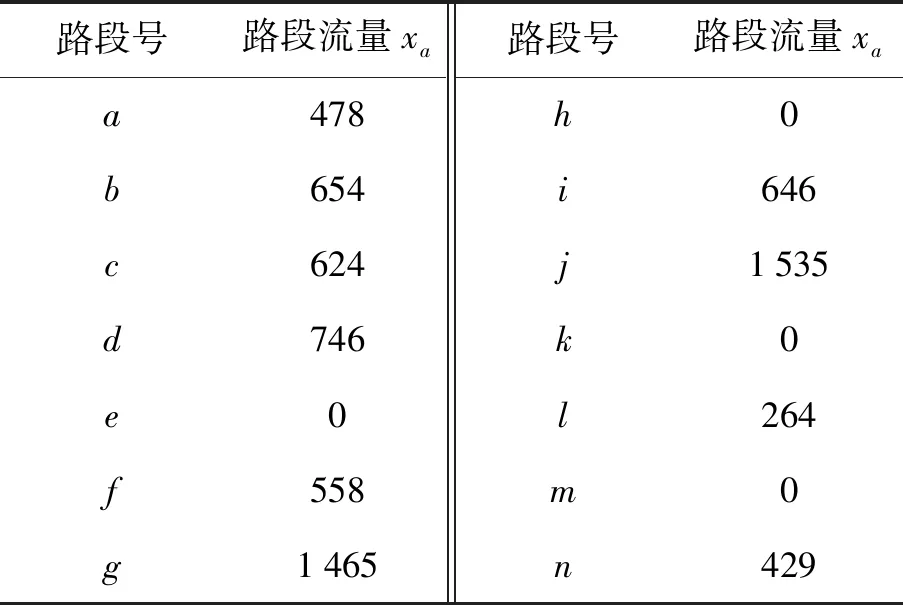
表5 改进算法计算所得的各路段的流量

结果表明，改进后的Frank-Wolfe算法和原Frank-Wolfe算法所得路段交通量存在较大的差别.如表6和表7所示，路段b连接交叉口1和交叉口3，在使用原算法求解时，OD对25的最短路径为2→1→3→5，OD对16的最短路径为1→3→5→6，均包含路段b；在使用改进算法求解时,考虑到交叉口3信号控制的影响，在进行交通流分配时交叉口1到交叉口3的时间成本增加，因此OD对16不选择路段b，而转为选择出行时间成本相对较小的路段c，所以路段b的流量采用改进后的算法减少47(veh)，而路段c的流量采用改进后的算法增加49(veh).路段g连接交叉口3和交叉口5，使用原算法求解时，OD对25、OD对45、OD对16、OD对36的最短路径均包含路段g；在使用改进算法求解时,考虑到交叉口5信号控制的影响，在进行交通流分配时交叉口3到交叉口5的时间成本增加，因此OD对16选择路段d ，OD对36选择路段i，因此路段g的流量采用改进后的算法减少45(veh)，而路段d的流量增加47(veh).

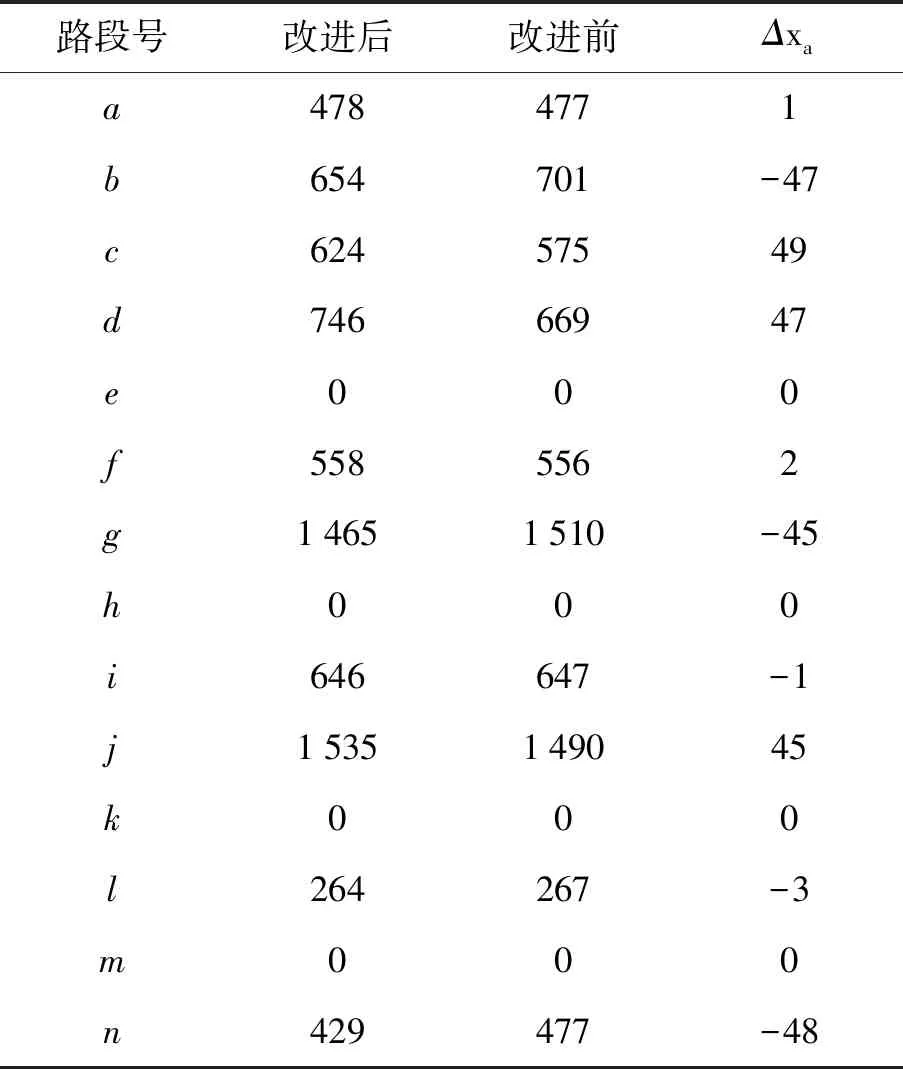
表6 原算法计算所得的各路段的流量

除了各路段流量发生变化外，各个OD对之间最短路径的阻抗值也发生变化.如表7所示，在使用改进Frank-Wolfe算法求解后最短路径的阻抗值均大于原Frank-Wolfe算法所得结果，是因为在求解阻抗函数时，考虑了信号控制延误的影响，所以阻抗值增加.因此，通过各个路段流量和路径阻抗之间的对比分析，说明交叉口信号配时对交通流量分配具有较大的影响，因此在进行流量分配时考虑交叉口信号控制引起的延误，所得的结果更加符合实际的交通流分布情况.

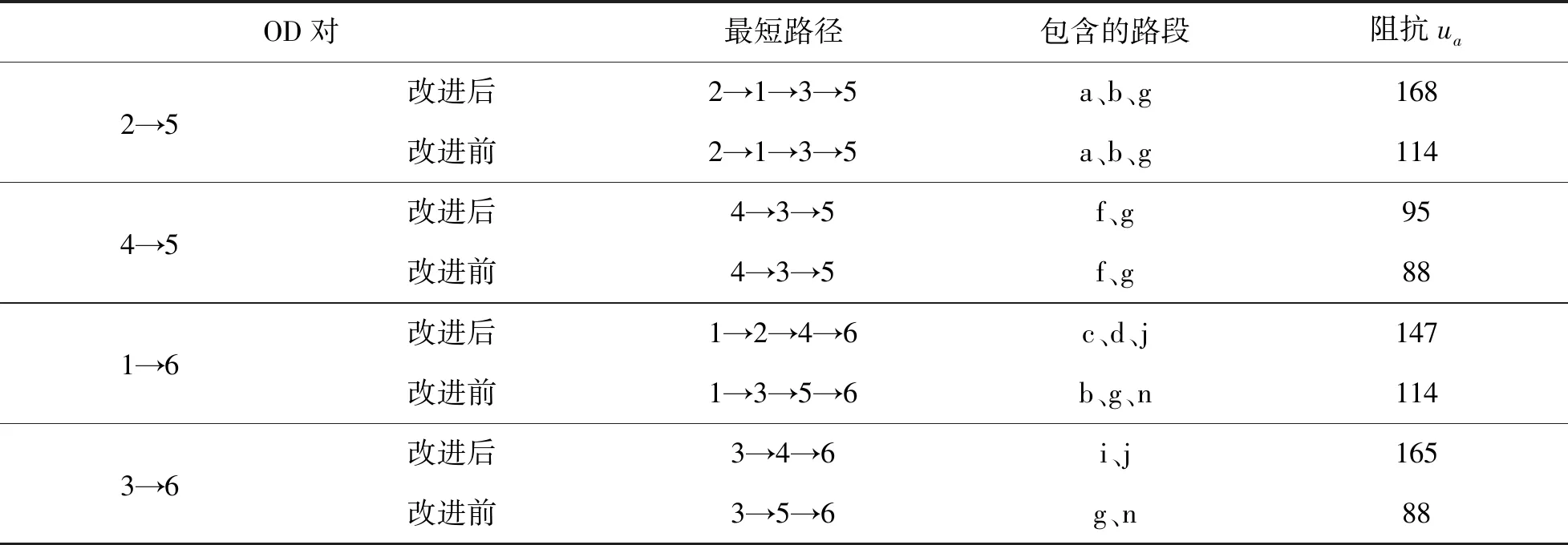
表7 最短路径比较

5 结束语

本文考虑了路网在受到交叉口信号控制的影响下，如何进行交通流分配.与其他求解算法不同的是，该算法在求解最短路径的时候考虑到交叉口信号控制引起的延误，并将其以惩罚值的形式加入到计算过程中，通过算法分析和算例验证，得出以下结论：

1)将由交叉口信号控制所引起的延误以惩罚值的形式加入到最短路径的求解过程中，所得的结果更加符合实际的交通流分布情况.

2)基于路网中信号控制对车辆的影响，对原Frank-Wolfe算法进行改进，考虑路网中交叉口信号控制的影响，将由信号控制所引起的延误以惩罚值的形式加入到阻抗函数中，通过更新阻抗函数，确定OD对间的最短路径进而求解出各路段相应的路段交通量.

由于交通系统本身的复杂性和不确定性，研究的过程中还存在着许多不足，今后需从以下几个方面继续研究和关注：

1)该算法仅得到各个路段的交通量，需要经过进一步的计算才能得到路径交通量.

2)为了计算简便，在计算的过程中假设车辆在交叉口的等待时间不会超过1个信号周期.在之后的研究中，可将车辆在交叉口的等待时间超过1个信号周期情况考虑进去.

3)交通流分配方面.由于交通流在路网中是实时变化的，并且交通需求也不是固定不变的，所以可考虑建立动态交通流分配模型.