基于负二项模型的高速公路安全影响要素研究

段洪琳，吴大勇，程 丽，郭 淼，伍毅平

(1.招商新智科技有限公司，北京 100070；2.北京工业大学城市交通学院，北京 100124)

道路交通安全是全球范围内面临的公共安全问题之一，也是我国面临的主要交通问题.据世界卫生组织2018年最新的研究报告显示，在我国因道路交通事故死亡的总人数位居世界第二，道路交通安全问题不容忽视[1].在联合国提出的可持续发展目标中明确指出：“到2020年将全球道路交通死亡人数减少到2015年的50%”[2].通过对我国31个省市道路交通事故的研究表明，除湖南省外，全国其他各省市均难以达到联合国制定的可持续发展目标[3].作为提升道路交通安全的基础，明确道路交通事故影响要素，是有针对性制定交通管控措施从而改善道路交通安全问题的前提.

截至2019年，我国高速公路总里程已超过14万km，位居世界第一.高速公路作为流量大、速度快、行车种类多、封闭性强的高等级公路，发生交通事故的数量多，其后果和影响程度也比城市道路更为严重.影响高速公路交通安全的因素主要包括人、车、路以及环境因素.研究表明，在我国的道路交通事故中有90%以上是由于驾驶员操作不当(如车速控制不当、不合理环道等)导致的[4]，国外的研究也表明：由于驾驶员的风险驾驶行为导致的交通事故占比高达95%[5-6].同时，以车辆运行状态为主的交通流因素也是影响交通事故的主要指标，高速公路的事故受交通流量、饱和度以及车辆速度分布特征等要素的影响[7]，特别是交通流特征与交通事故严重程度之间存在显著关系[8].另外，道路因素对于交通事故的影响占37%～41%[9]，包括道路的圆曲线、缓和曲线、直线、竖曲线、坡度等道路几何条件[10].通过研究道路几何条件对于高速公路交通事故的影响关系，可为高速公路的前期设计与后期管控提供支撑.此外，环境因素也是导致交通事故的诱因之一，以天气条件的影响最为显著[11].雨、雪、雾等恶劣天气不仅会影响驾驶员的视线，进而导致驾驶员对于刹车距离判断的准确性，延长车辆的制动距离[12]，也会影响道路表面的状态，导致道路结冰、湿滑进而增加车辆碰撞的风险和交通事故发生的几率[13].

在道路交通安全影响要素分析方法中，国内外学者也进行了较为丰富的研究.如胡骥等[14]使用有序Logit与Probit模型研究了路面状况、道路线型等因素对翻车事故的影响.Yan等[15]使用逻辑回归模型研究了交通事故特征与车道数、限速值等要素之间的关系.Wang等[16]使用带有不同关联函数的广义估计方程研究了追尾事故之间的相关性.Shinohara等[17]使用卡方检验分析了安全带和车型对驾驶员及乘客受伤程度的影响.由于交通事故数据具有随机性、离散型以及非负性的特点，一些学者开始使用泊松回归模型研究道路交通事故及其影响要素之间的关系[18-19].这一方法要求交通事故数的均值等于方差，但是通常情况下交通事故数的均值与方差是不等的，这在一定程度上影响了模型的精度.因此，有研究人员提出在泊松回归模型中加入由于均值与方差不相等而导致的误差项，转化为使用负二项回归模型来研究这一问题，能提高模型的精度[20].其中，事故数据统计间隔的确定是使用负二项回归模型的关键所在.

本文以广西省桂林市境内的G65包茂高速部分路段发生的交通事故及其影响因素之间的关系为研究对象，使用负二项回归模型，分析发生在该路段上的交通事故与道路几何条件、交通流条件、道路设施条件之间的关系，以探究影响高速公路安全的显著要素.通过对影响要素的弹性分析，确定各影响要素对该路段交通事故的影响程度，为科学制定交通事故预防措施，提高高速公路安全性水平提供理论支持.

1 基于负二项回归的交通安全分析模型

1.1 模型构建

高速公路交通事故的发生与否具有随机性、小概率性的特点，并且交通事故沿高速公路的时空分布具有离散性、整数性的特点.因此，可使用泊松分布来描述交通事故在高速公路路段上的分布特征，泊松回归模型也常用于道路交通事故的研究，其分布形式见式(1)

(1)

式中：ni为第i个路段发生交通事故的数量；λi为第i个路段上发生交通事故次数的期望值，并且λi可被看作事故影响因素的函数，见式(2)

λi=exp(βjXij)

(2)

式中：Xij为第i个路段上影响交通事故的第j个自变量；βj为Xij的系数.

泊松回归模型适用于均值与方差相等的交通事故数据，但是高速公路上的交通事故数据通常具有过度离散或者离散不足的特点(即均值小于方差或者均值大于方差). 而负二项回归模型作为泊松回归模型的一般形式，能更好地拟合这种类型的交通事故数据，即当事故数据的均值不等于方差时，泊松回归模型将产生误差，此时事故影响因素的函数λi转换为式(3)：

λi=exp(βjXij+ε)

(3)

式中：ε为当事故数据的均值不等于方差时泊松模型产生的误差项；exp(εi)为均值为1、方差为D的伽马分布的误差项. 将式(3)带入泊松回顾模型中，得到含有误差条件的泊松回归模型：

(4)

对式(4)进行化简，消去误差项ε，得到负二项回归模型：

(5)

式中：K为离散系数；Γ为伽马分布.

1.2 模型检验

从2个方面对所建立的负二项模型进行检验，即拟合优度检验和准确性检验. 其中拟合优度检验采用赤池信息量准则(AIC)进行检验；准确性检验采用相对误差和累积残差进行检验. 各指标的计算方法如下.

1)赤池信息量准则(AIC)是由日本统计学家Akaike提出的，计算方法见式(6)：

AIC=-2lg(L)+2p

(6)

式中：L为负二项回归模型的最大似然值；p为负二项回归模型中估计参数的个数. 其判断标准为该值越小，表示所建立的负二项回归模型的拟合效果越好.

2)相对误差表示由负二项回归模型得到的事故数的预测值与实际值之差的绝对值与实际值的比值，其计算方法见式(7)：

(7)

式中：Re为相对误差值；n为给定高速公路实际发生的交通事故次数之和；n′为使用负二项回归模型得到的该高速公路交通事故次数预测值之和. 其判断标准为该值越小，表示所建立的负二项回归模型的准确性越好.

3)累积残差为标准残差之和，标准残差表示由负二项回归模型得到的事故数的预测值与实际值之间的差别，其计算方法见式(8)：

(8)

式中：CSR为累积残差；ni为高速公路第i个路段上发生的交通事故次数的实际值；n′i为高速公路第i个路段上由负二项回归模型得到的交通事故次数的预测值；u为路段总数. 其判断标准为该值越小，表示所建立的负二项回归模型的准确性越好.

1.3 弹性分析

与传统的线性回归模型不同，负二项回归模型属于非线性回归(或广义线型回归)模型的范畴，某一自变量对因变量影响程度不仅取决于模型中该自变量系数值的大小，即：存在某些自变量虽然与因变量显著相关，但其影响程度可能很小. 因此，使用弹性分析方法来量化各自变量对因变量的影响程度. 其计算方法见式(9)：

(9)

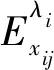
当自变量为连续型变量时，为了计算方便，式(9)可使用式(10)近似计算：

(10)

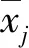
当自变量为离散型变量时，为了计算方便，式(10)可使用式(11)近似计算：

(11)

最终，根据各自变量弹性系数计算结果的绝对值的大小来确定模型中该自变量对因变量影响程度的大小.

2 案例分析

2.1 数据描述

本文的研究数据来自于广西省桂林市境内的G65包茂高速部分路段统计的事故数据，该部分高速公路全长108 km，属于招商公路桂林公司的运营管理范畴.包茂高速广西省桂林市境内部分路段的空间位置，如图1所示.该路段组成复杂，所经区域多桥梁、隧道、服务区、收费站等，全线共设桥梁23座，其中：大桥7座，中桥1座，小桥1座；分离式立交大桥1座，分离式立交中桥7座，分离式立交小桥3座；互通立交跨线大桥1座，互通立交跨线中桥2座.整体式连拱隧道1座，分离式隧道3座.互通立交2处，收费站5处，服务区3处.此外，沿线共设4个交调站用于调查经过该路段车辆的交通流状态，其中客车的年平均日交通量为0.61万辆/d，平均速度为99.87 km/h；货车的年平均日交通量为0.11万辆/d，平均速度为74.06 km/h.该路段交通事故频发，且事故形态以碰撞护栏事故为主，据公司统计2017年1月至—2019年12月该路段共发生碰撞护栏交通事故524起，照成的生命及财产损失较为严重.

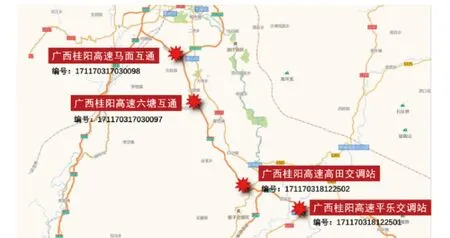
图1 包茂高速广西省桂林市境内部分路段

2.2 路段划分

事故数据统计间隔即路段长度的确定是使用负二项回归模型的关键所在，通常使用1 km长度的路段作为研究单元[21].路段划分长度的大小将直接影响到道路的几何条件、交通流条件、道路设施条件以及交通事故等因素的统计特征，进而影响模型的精度以及应用效果.为了探索适合本文研究的高速公路路段划分长度，采用逐步逼近的思路分别将路段划分为1、2、3、4、5、6 km，分别代入模型中检验模型的拟合效果.经过计算发现，传统的将路段划分为1 km的做法并不适用于本路段，随着路段划分长度的增加，从1～5 km模型的拟合精度逐渐增加；而将路段长度划分为6 km时模型的拟合精度又开始下降，即5 km是适合该高速公路最佳的研究单元.

2.3 变量描述

以5 km为间隔将高速公路划分为44个路段.统计每个路段上的交通条件数据、交通设施数据以及道路几何条件数据，从这些数据中选取影响交通事故次数的潜在自变量，其中，交通条件自变量包括：客车的年平均日交通量、货车的年平均日交通量、客车的平均速度、货车的平均速度；交通设施数据包括：隧道数、匝道数；道路几何条件数据包括：圆曲线长度、缓和曲线长度、直线长度、坡长、竖曲线半径.3个方面共计11个变量，各自变量的名称、单位以及统计特征见表1.

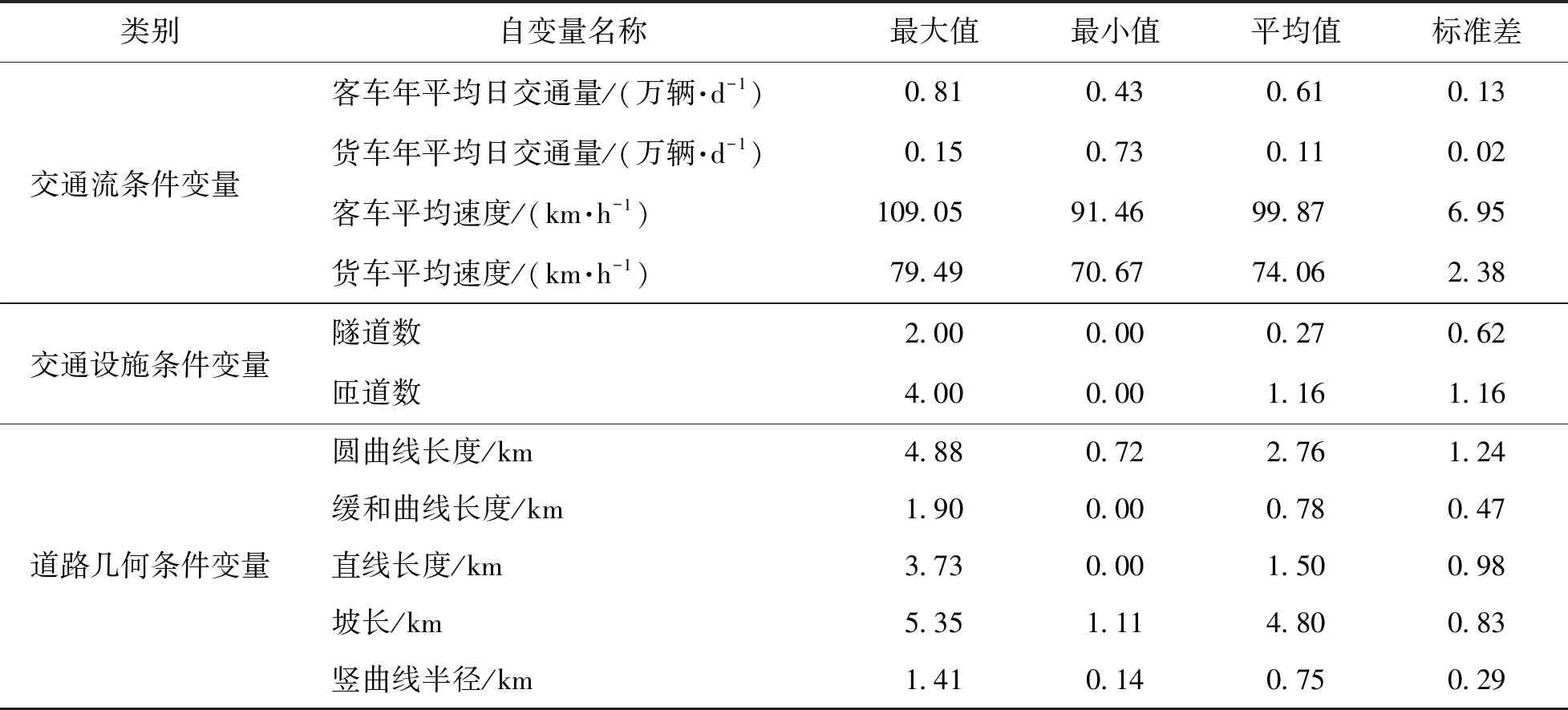
表1 自变量特征描述

2.4 模型构建

在模型构建过程中，首先将变量分为两类：连续变量和分类变量，其中表1中的交通条件变量、道路几何条件变量设置为连续变量，交通设施条件变量设置为分类变量，并且对分类变量中的隧道数、匝道数进行哑变量处理，使用0、1代表交通设施条件的有无以及数量的多少；其次，由于客车年平均日交通量、货车年平均日交通量、客车平均速度、货车平均速度等变量的数据方差较大，有可能导致数据的不稳定性增加，因此在不改变数据相对关系的情况下对数据进行对数变换以提高模型的稳定性.

对模型的拟合优度检验和准确性检验结果见表2.采用逐步回归方法得到最终的模型，通过比较发现，初始零模型的AIC值为293.340，最终模型的AIC值为244.210，表明最终模型的拟合优度相比于初始模型有明显地提高.最终，3个维度包含的11个自变量中，剔除了圆曲线、缓和曲线以及直线的长度、竖曲线半径等4个自变量，剩余的7个自变量为：客车年平均日交通量、货车年平均日交通量、客车平均速度、货车平均速度、隧道数、匝道数、坡长.

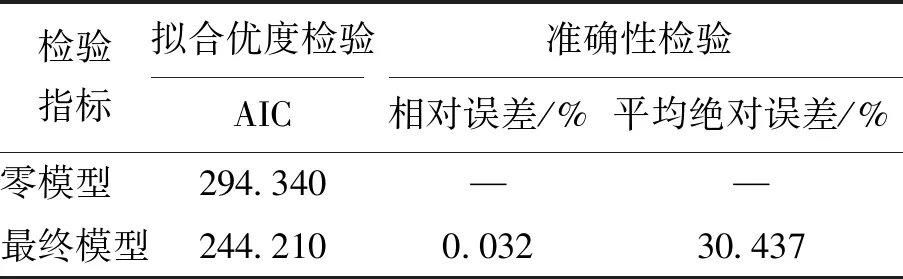
表2 负二项回归模型拟合优度与准确性检验结果

从表2可知，当模型中考虑客车年平均日交通量、货车年平均日交通量、客车平均速度、货车平均速度、隧道数、匝道数、坡长等对交通事故起数的影响时，模型的AIC值为244.210，模型的相对误差为0.032%，平均绝对误差为30.437%.可见模型的拟合效果与准确性良好.将路段上实际发生的交通事故数与由模型预测的交通事故数进行比较，结果如图2所示.

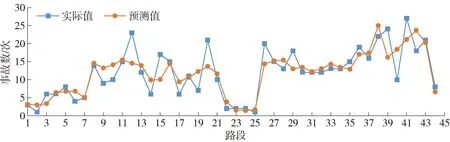
图2 交通事故起数实际值与预测值路段分布比较

本文旨在通过负二项模型分析高速公路的安全影响要素，因此采用全样本数据库对模型进行拟合[22].

由图2高速公路路段交通事故起数实际值与预测值的比较可知，本文所构建的用于研究高速公路安全影响要素的负二项回归模型能反映高速公路交通事故发生的趋势，综合考虑模型的拟合优度与准确性认为本文所构建的负二项回归模型能揭示广西省桂林市境内的G65包茂高速部分路段的交通事故及其影响要素之间的关系.

利用统计分析软件R3.6.3对本文所使用的负二项回归模型进行求解，采用逐步回归，剔出不显著因素，得到简化模型.简化模型的参数估计结果，见表3.

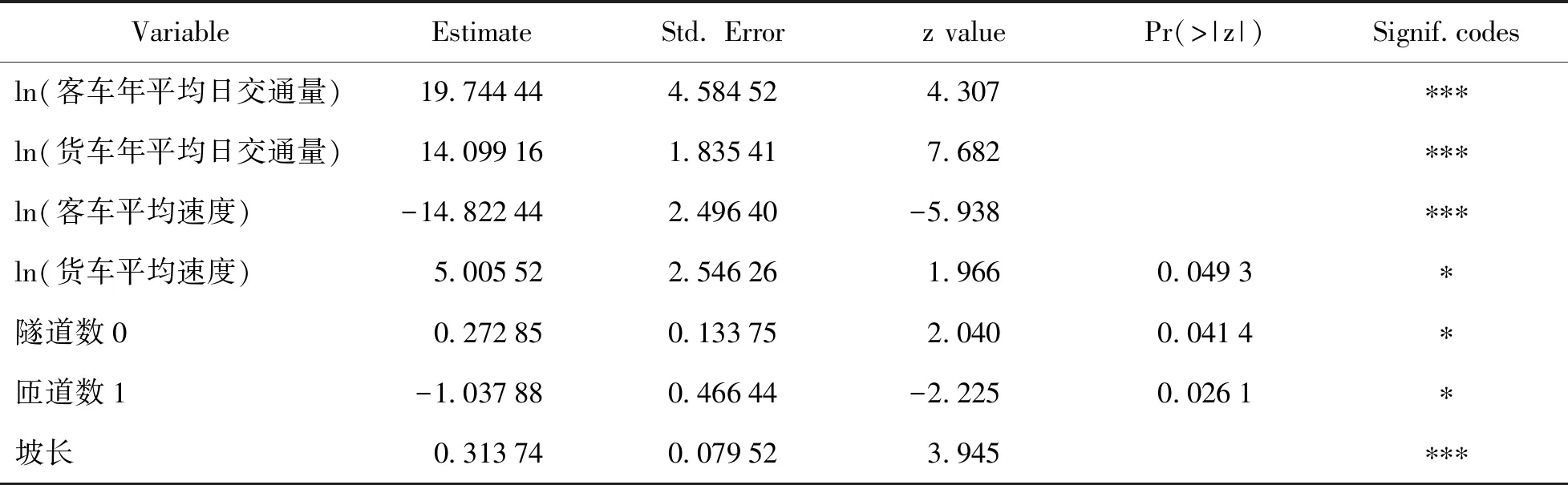
表3 模型逐步回归分析结果

在0～0.001之间是非常非常显著，通常用“***”号表示；在0.001～0.01之间是非常显著，通常用“**”号表示；在0.01～0.05之间是比较显著，通常用“·”号表示；在0.05～0.1之间是显著，通常用“”号表示；在0.1～1之间是不显著.

从表3可知，拟合优度最好的模型包含7个变量：客车年平均日交通量、货车年平均日交通量、客车平均速度、货车平均速度、隧道数、匝道数、坡长.这些变量的显著性检验p值均小于0.05，其他显著性检验p值大于0.05的变量与交通事故起数没有显著相关关系，故未列入表3中.

2.5 弹性分析

为了进一步探索各自变量对因变量影响程度的大小，使用弹性分析方法对模型中具有显著性的变量进行弹性分析，结果见表4.

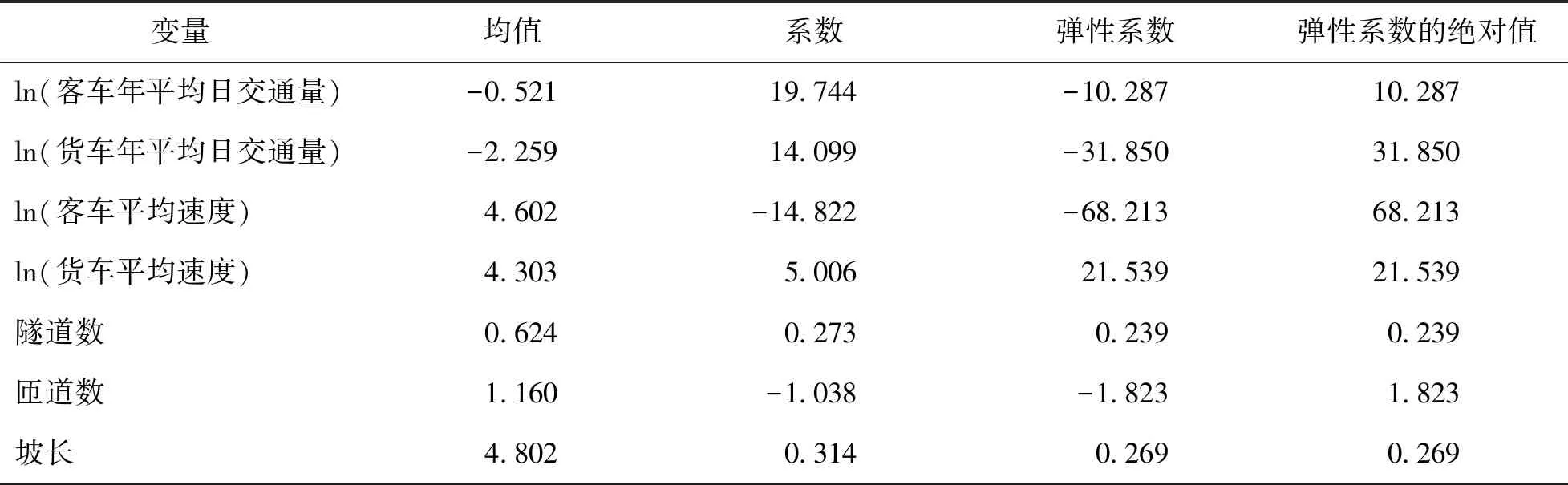
表4 弹性分析结果

从表4可知，自变量对因变量的影响程度的排序依次为：其中除客车平均速度和匝道数以外，其他变量均呈现正影响.

3 结束语

本文采用负二项回归模型对广西省桂林市境内的G65包茂高速部分路段的交通流条件、交通设施条件、道路几何条件等安全影响要素进行了系统研究，模型拟合效果良好.研究结果表明，交通流条件变量、交通设施条件变量、道路几何条件变量均在一定程度上影响高速公路的安全性，其中以交通流条件高速公路交通安全的影响最大，包括客车平均速度、货车年平均日交通量、货车平均速度、客车年平均日交通量，因此高速公路运营管理部门应重点加强对高速公路交通流的监测与管控，适时控制道路上的车流量与行车速度，以提高高速公路的安全性.此外，交通设施条件中的匝道数和隧道数两个变量，道路几何条件中的坡长变量也对该高速公路的交通安全具有显著影响，但其影响程度比交通流条件变量小，建议在该类路段处设置必要的安全提示.

由于数据限制，本研究仅使用车辆碰撞护栏这一事故形态代表高速公路的安全性，且未考虑道路交通标志的影响，后续将完善数据资源以进一步提高将负二项回归模型用于该道路进行安全影响要素分析的拟合优度与准确性.高速公路交通安全是我国乃至全世界共同关注的热点问题，根据不同地区高速公路的特点有针对性地研究其安全影响要素，逐步提高全国各地区高速公路的安全性，对于实现联合国制定的2020年可持续发展目标具有重要意义.